BK TP.HCM
BK TP.HCM
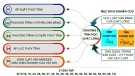
Bài 1 Cho 1 cơ hệ như hình vẽ (hình 1). Cho biết: , P1, P2. a.Hệ đã cho có luôn cân bằng với mọi loại tải tác động không? Tại sao? b.Nếu hệ cân bằng, hãy xác định các phản lực liên kết của các liên kết ngoại. c.Hãy xác định các ứng lực lên từng thanh thẳng trong hệ.
Hình 1
1
BK TP.HCM
1. Hệ đã cho là hệ giàn phẳng vì hệ thỏa mãn tất cả 4 điều kiện sau đây:
Tất cả các vật rắn trong hệ đồng phẳng và tải tác động cùng nằm trong mặt phẳng của hệ.
Tất cả các vật rắn trong hệ đều là các thanh thẳng và có thể bỏ qua trọng lượng của chúng.
Hai đầu cuối của mỗi thanh
Hình 1
thẳng có hai khớp bản lề.
BK TP.HCM
Tất cả các thanh thẳng trong hệ không chịu tác động của lực và moment ở giữa thanh mà chỉ chịu tác động của các lực tập trung tại các đầu cuối của các thanh.
Hệ thỏa mãn cả 4 điều kiện nêu trên sẽ được gọi là hệ giàn phẳng.
Hình 1
2
BK TP.HCM
2. Tính chất của hệ giàn phẳng:
Tất cả các thanh trong hệ giàn phẳng chỉ chịu lực nén
hoặc lực kéo dọc trục.
Thanh chịu nén
Ứng lực
Thanh chịu kéo
Hai lực tác động lên 2 đầu cuối của mỗi thanh thỏa tiên đề 1 của tĩnh học và được gọi là các ứng lực tác động lên từng thanh trong hệ giàn.
BK TP.HCM
Nút giàn là nơi nối các thanh trong hệ giàn lại với nhau. Số khớp bản lề nội k ở mỗi nút giàn có t thanh nối với nhau được tính theo công thức:
k = t – 1
Với k: là số khớp bản lề nội tại
Nút giàn
nút khảo sát, t: là số thanh nối
vào nút đó. A, B, C: là các nút
giàn
3
BK TP.HCM
Nút giàn
Mỗi thanh trong hệ giàn sẽ tác động 1 lực lên nút nối với nó. Lực này có phương trùng với đường thẳng của thanh, cùng độ lớn với lực do nút tác động lên thanh này nhưng ngược chiều.
BK TP.HCM
a. Tính bậc tự do của hệ:
Ta có 2 khớp bản lề ngoại cố định và 4 khớp bản lề nội.
Lý thuyết:
+ Nếu dofhệ ≤ 0 thì hệ luôn cân bằng với mọi loại tải tác động.
+ Nếu dofhệ > 0 thì hệ không luôn cân bằng với mọi loại tải.
Vậy hệ luôn cân bằng với mọi loại tải tác động vì dofhệ = 0
4
BK TP.HCM
b. Xác định các phản lực của các liên kết ngoại.
Khảo sát sự cân bằng
của toàn hệ
Tự do hoá hệ (bỏ hết các liên kết ngoại):
YD = 0
Do thanh DC chỉ bị kéo nén theo phương X nên chỉ tạo ra phản lực theo phương x. Do đó YD = 0.
BK TP.HCM
Viết các phương trình cân
bằng cho hệ lực:
5
BK TP.HCM
Giải hệ (1), (2), (3) ta nhận được:
(2) YA = P2 > 0 (3) XD = – (P1 + P2) < 0
(1) XA = – P1 – XD = – P1 – [–(P1 + P2)] = P2 > 0
Do XD < 0 nên chiều đúng của XD ngược chiều đã chọn.
BK TP.HCM
c. Dùng phương pháp tách nút:
Để tính được ứng lực tác động lên các thanh trong hệ giàn thông thường người ta dùng phương pháp tách nút. Nghĩa là tách riêng từng nút trong hệ giàn để khảo sát sự cân bằng của nút đó.
Ứng lực tác dụng lên thanh CD – thanh (hình 3)
Hình 3a
SC, = XD SC, = (P1 + P2)
6
BK TP.HCM
Khảo sát sự cân bằng của nút C
Ta có:
BK TP.HCM
Ứng lực tác dụng lên & :
7
BK TP.HCM
Khảo sát sự cân bằng nút B (hình 4).
Ta có:
Hình 4
BK TP.HCM
6 m 8 m
Bài 2
C
A
8 m
B P2
P1
P1 = 800 N P2 = 400 N Tìm các phản lực tại gối C và cho biết các thanh chịu kéo hay chịu nén?
8
BK TP.HCM
Xét nút B
y
FBA FBC
(1.1)
450 400 N x
B
(1.2)
800 N
Giải 2 pt (1.1) và (1.2)
(thanh chịu kéo)
(thanh chịu kéo)
BK TP.HCM
Xét nút C
y
FCA x C
(thanh chịu nén)
450
Cy FBC
9
BK TP.HCM
Bài 3
C P1 A P2 B
450 450
4 m
D E
4 m 4 m
Hãy cho biết các thanh chịu kéo hay chịu nén?
P1 = 600 N P2 = 400 N
BK TP.HCM
Xét nút A
y
600 N
(thanh chịu nén)
A FAB x
450
FAD
(thanh chịu kéo)
10
BK TP.HCM
Xét nút B
y
400 N
600 N FBC B x
(thanh chịu nén)
FBD
(thanh chịu kéo)
BK TP.HCM
Xét nút D y
400 N 848,528 N FDC
450 450 x
D
(thanh chịu kéo)
FDE
(thanh chịu nén)
11
BK TP.HCM
Bài 4
D 2 r
c 1 3
A B C a b y
+
x
W
Cho W = 80 N a = 6 m, b =9 m, c = 3 m, r = 0,5 m Tìm các thành phần phản lực tại A, B và C.
BK TP.HCM
Xét vật 1
W
Ax W Ay
12
BK TP.HCM
By a b Ax Cx
Bx Ay Cy
Xét vật 3
BK TP.HCM
b D y
Xét vật 2 Dx c - r W
r
Bx By
13
BK TP.HCM
By a b Ax Cx
Bx Ay Cy
Xét vật 3
BK TP.HCM
D
Bài 5
P
l 450 q B C
M 2 l l
E 2 l
l α = 600 F A
14
BK TP.HCM
a) Hệ đã cho có luôn cân bằng với mọi loại tải khác hay không? b) Hãy tìm các phản lực liên kết tại A và C ứng với hai trường hợp của lực P
i) P = ql ii) P = 2ql
Cho biết l, moment M = 4ql2 Bỏ qua trọng lượng của vật và ma sát.
BK TP.HCM
a) Tính bậc tự do của hệ
Vậy hệ đã cho không luôn cân bằng dưới mọi tác động
15
BK TP.HCM
D
P
Điều kiện để hệ cân bằng là thanh DF phải cân bằng hay Nc > 0 (1)
l
Khảo sát sự cân bằng của thanh DF
NC
Tự do hóa thanh DF
C
Viết pt cân bằng
(2)
M y l
(3)
+
E x
l α = 600
Thay (3) vào (1), ta có đk để hệ cân bằng
F
(4)
BK TP.HCM
D
P
i) Cho P = ql. Ta có (4) thỏa. Vậy hệ cân bằng. Lúc này
l NC
C
M y
Khảo sát sự cân bằng của khung ABC Tự do hóa khung ABC
l
+
E x
l α = 600 F
16
BK TP.HCM
Khảo sát sự cân bằng của khung ABC. Tự do hóa khung ABC
NCx B C
Viết các phương trình cân bằng
(5)
Q = ql 2 l α NC NCy
(6)
2 l y 4/3 l
(7)
+
x A XA
MA YA
BK TP.HCM
NCx B C
α Q = ql 2 l NC NCy
2 l y 4/3 l
+
x A XA
MA YA
17
BK TP.HCM
B C
Q = ql 2 l
2 l Cho P = 2ql, ta có (4) không thỏa. Vậy hệ không cân bằng. Lúc này NC = 0 Khảo sát lại sự cân bằng của khung ABC y 4/3 l Giải lại hệ (5), (6) và (7) với Nc = 0
+
x A XA
MA YA
BK TP.HCM
Bài 6
b
a b
a b
a b
a
Các vật có trọng lượng bằng nhau. W = 0,0235 a = 3 b = 4 Tìm các thành phần lực ngoại tác dụng lên vật ở dưới cùng.
18
BK TP.HCM
Xét vật dưới cùng
W N b a NA
NB
BK TP.HCM
W
N1
N2
Xét cả hệ gồm 5 vật
N3
N4
NA
NB
19
BK TP.HCM
Xét vật dưới cùng
W N b a NA
NB