CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
27
Chng 2: TRNG THÁI *NG SU+T
2.1 *ng sut
2.1.1 *ng sut, N'i l,c
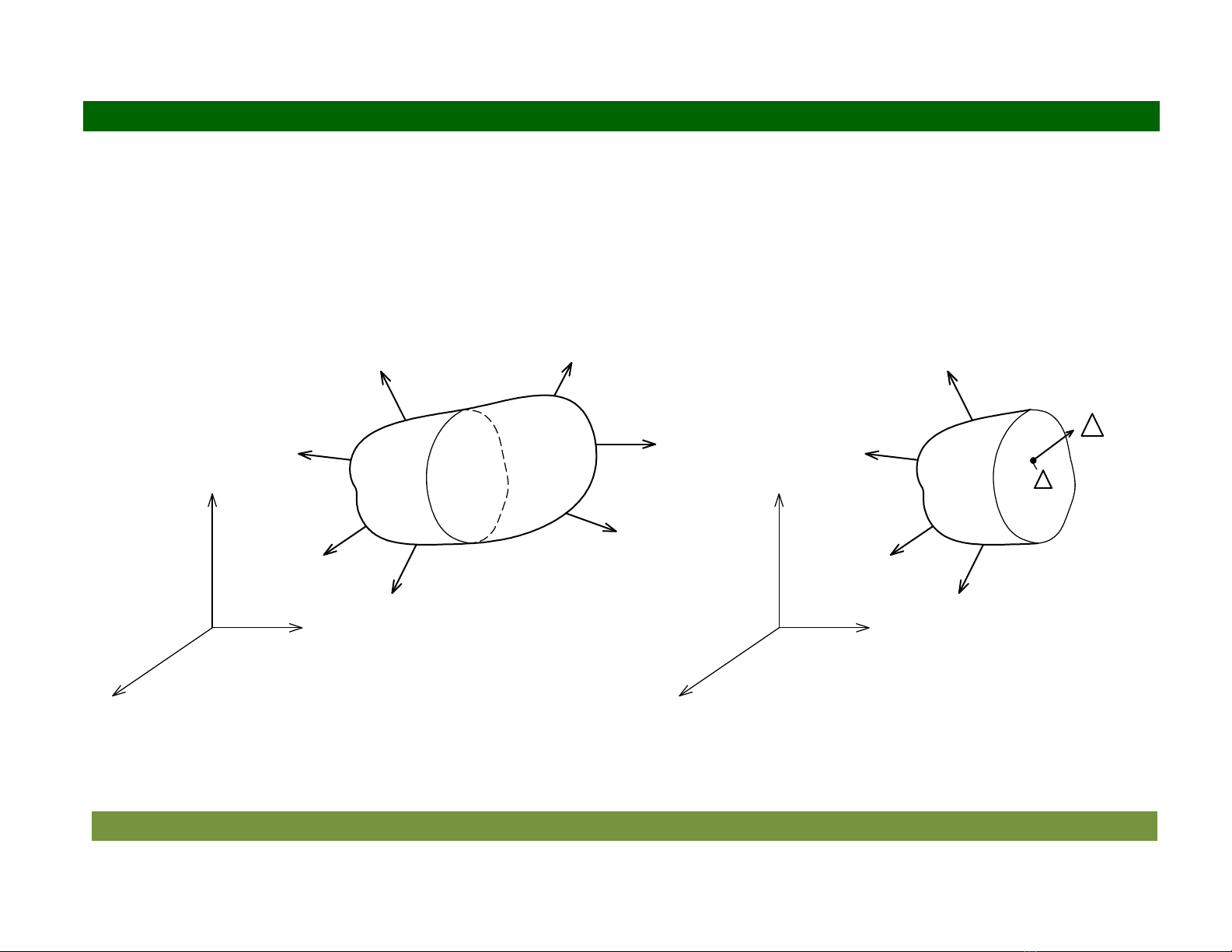
Hình 2.1 4ng sut ti m"t im
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
28
4ng sut trung bình ti im K:
tb
P
p
A
∆
=
∆
(2.1)
4ng sut ti im K:
v
A 0
P
p
A
lim
∆ →
∆
=
∆
(2.2)
a) b)
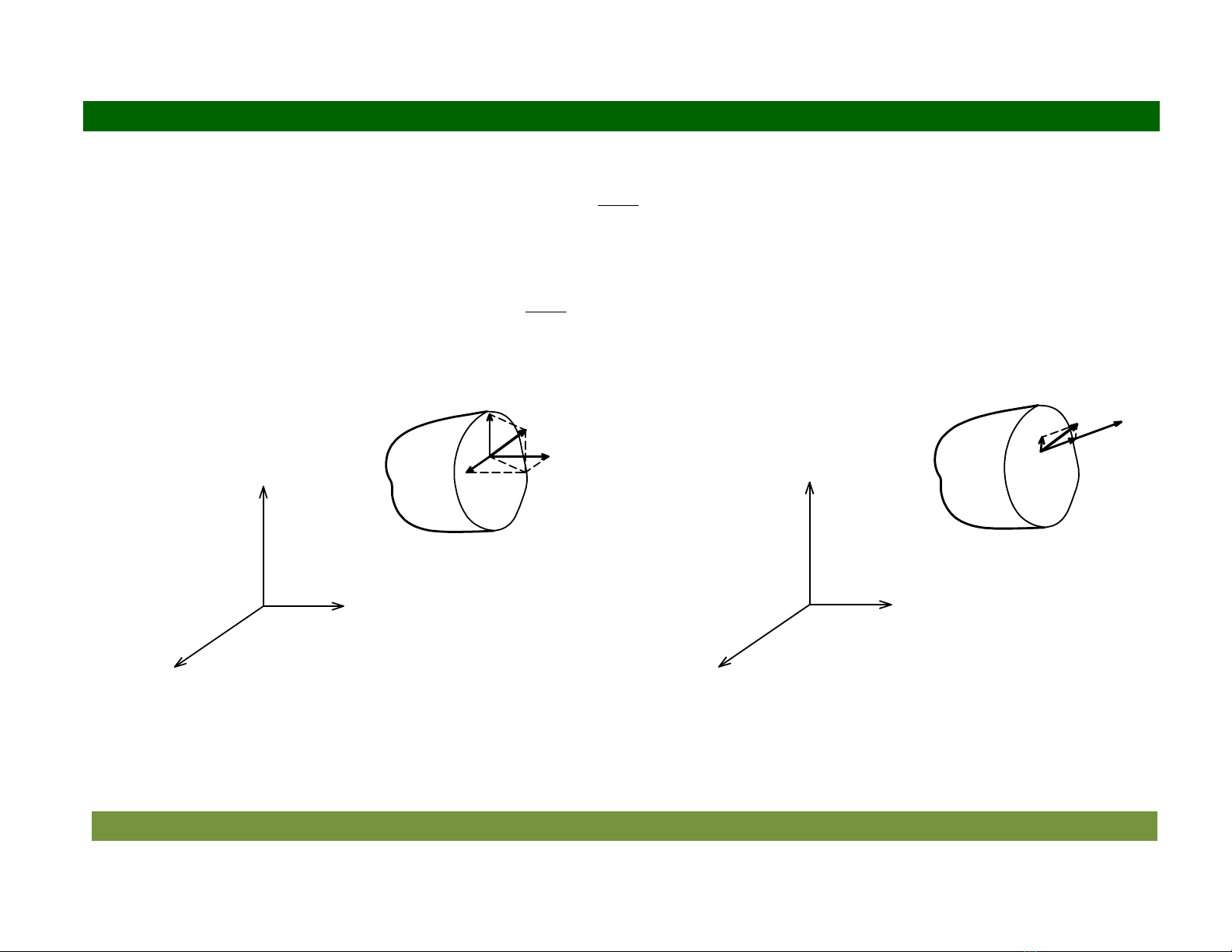
Hình 2.2 Các thành ph%n ng sut ti m"t im
4ng sut ti im K chiu lên các trc ta " (hình 2.2a):
ν
ν
1
ν
1
ν
3
ν
ν
σ
ν
τ
ν
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
29
v v1 v2 v3
p p p p
= + +
(2.3)
4ng sut ti im K phân ra hai thành ph%n (hình 2.2b):
v v
v
p
= σ + τ
(2.4)
trong ó:
v
σ
: có phng h ng theo phng pháp tuyn ca mt c't ngang và $c gi
là ng sut pháp;
v
τ
:có phng tip tuyn v i mt c't ngang và $c gi là ng sut tip.
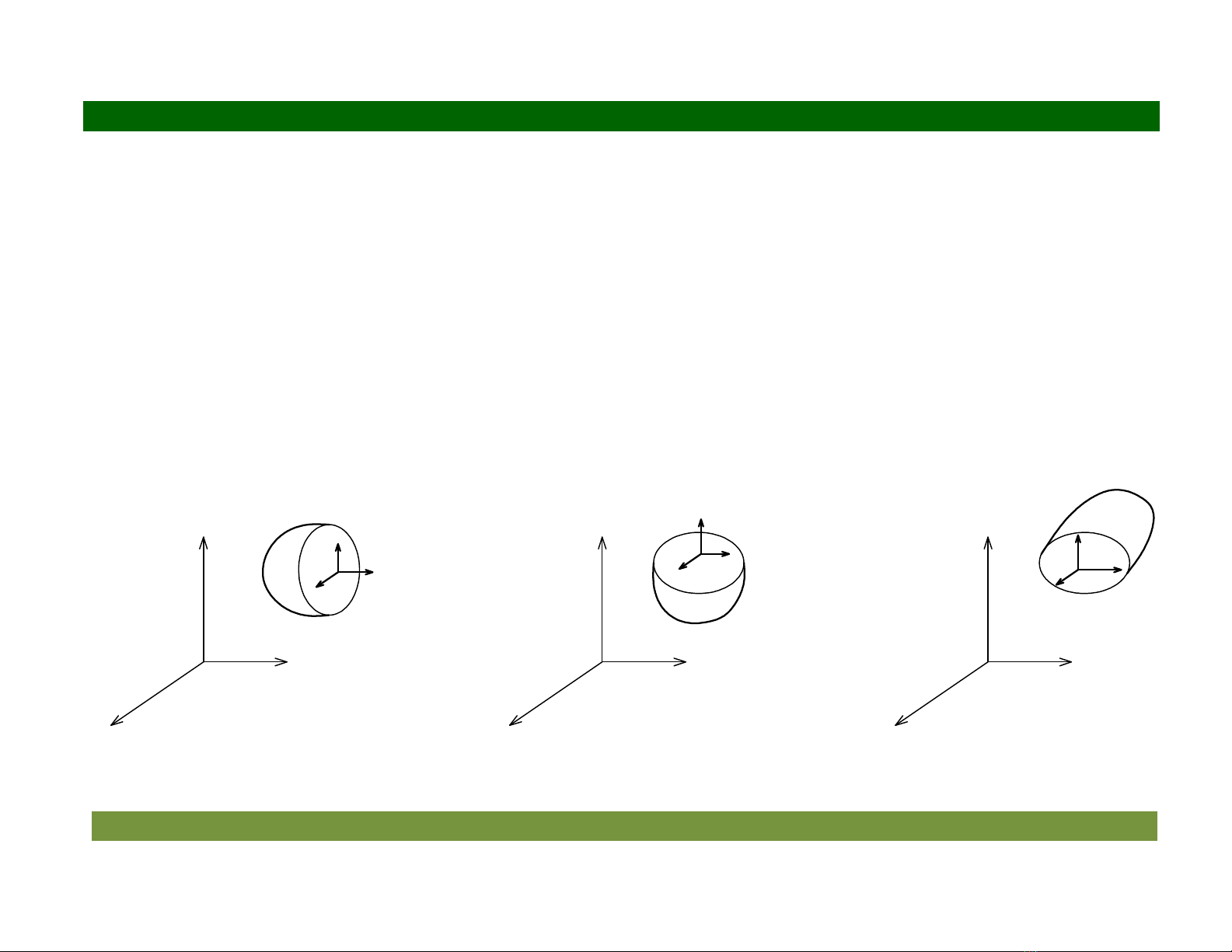
Hình 2.3 4ng sut trên các mt
11
σ
12
τ
13
τ
22
σ
21
τ
23
τ
33
σ
31
τ
32
τ
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
30
Trong trng h$p c bit khi h trc
1 2 3
ox x x
có 1 trc là vuông góc v i mt c't
ngang (ch+ng hn trc
1
ox
) thì ng sut
pháp theo phng trc
1
ox
$c ký hiu là
11
σ
; ng sut tip trên mt c't ngang lúc này
$c phân thành hai thành ph%n có phng
theo trc
2
ox
và
3
ox
$c ký hiu l%n l$t
là:
12
τ
;
13
τ
. Tng t nh vy, trên mt có
phng pháp tuyn là trc
2
ox
có các thành
ph%n ng sut:
22
σ
;
21
τ
;
23
τ
; trên mt có
phng pháp tuyn là trc
3
ox
có các thành
ph%n ng sut:
33
σ
;
31
τ
;
32
τ
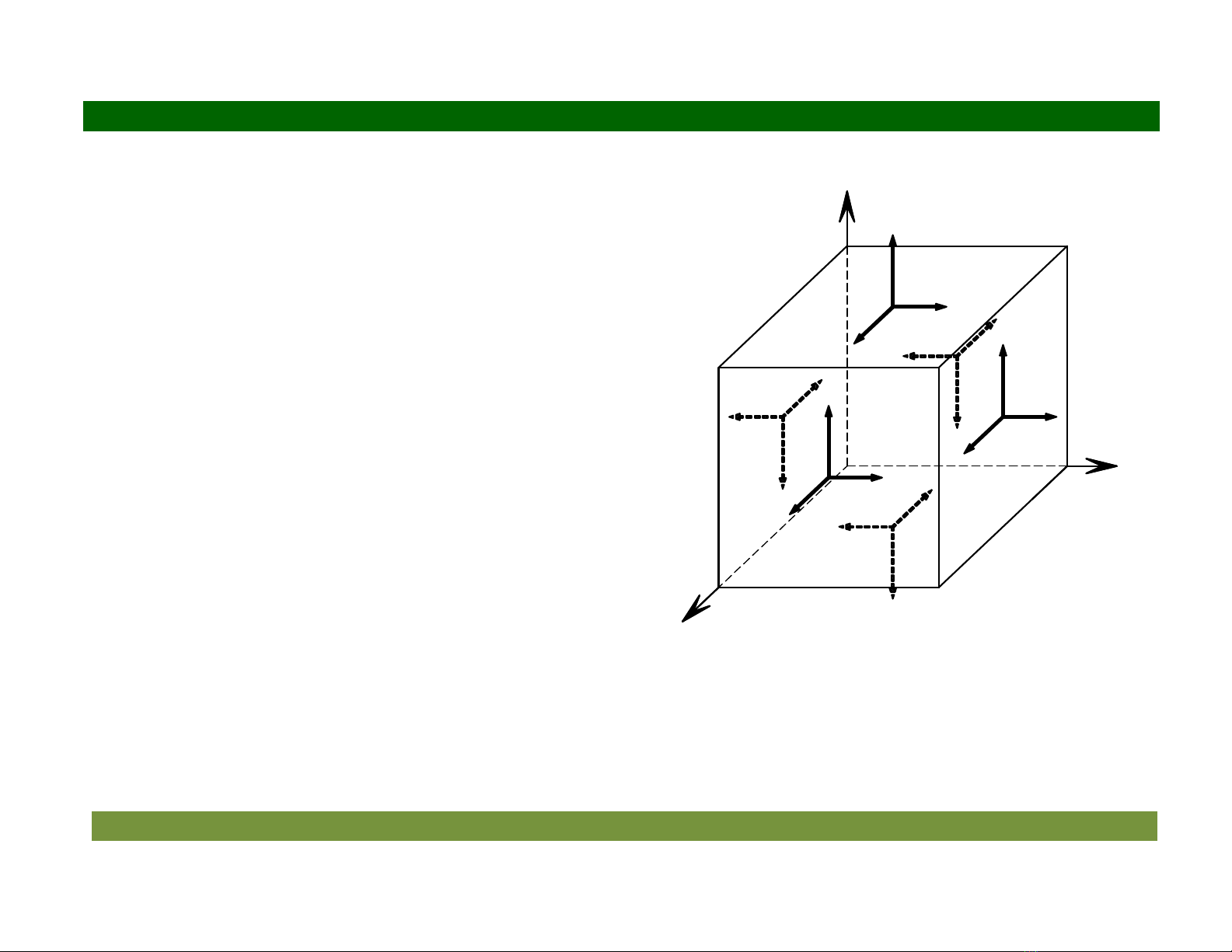
(hình 2.4).
Hình 2.4 4ng sut trên các mt ca
ph%n t lp phng
dx
3
dx
2
dx
1
σ
σ
σ
σ
σ
σ
τ
τ
τ
τ
τ
21
τ
τ
21
τ
τ
τ
τ
τ
x
1
x
2
x
3

CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
31
Ti m"t im bt k# trong vt th, khi tách ra m"t phân t hình lp phng mà các mt
ca phân t này có phng pháp tuyn l%n l$t trùng v i phng các trc ta " ca h
trc
1 2 3
ox x x
thì trên các mt ca phân t này có các thành ph%n ng sut (hình 2.4):
- 3 thành ph%n ng sut pháp:
11
σ
;
22
σ
;
33
σ
.
- 6 thành ph%n ng sut tip:
12
τ
;
21
τ
;
23
τ
;
32
τ
;
31
τ
;
13
τ
.
Quy #c cách vit ng sut tip: 4ng sut tip có hai ch3 s thì ch3 s %u tiên là ch3
s ca trc ta " có phng trùng v i phng pháp tuyn ca mt c't, ch3 s th 2 là ch3
s ca trc ta " có phng là phng ca véct ng sut.
Quy #c du ca các thành ph!n ng sut:
- i v#i ng sut pháp: 4ng sut pháp $c coi là dng khi có h ng cùng v i
h ng pháp tuyn ra ngoài ca mt c't.


















![Bài giảng Công nghệ sản xuất bia [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260224/diegomaradona04/135x160/85561772004812.jpg)







