VIETNAM NATIONAL UNIVERSITY – HCM CITY
UNIVERSITY OF SCIENCE
CHƯƠNG V:
ĐIỆN TỬ CƠ BẢN
1
KHUẾCH ĐẠI TÍN HIỆU NHỎ
Presenter: Nguyen Thi Thien Trang
CHƯƠNG V: KHUẾCH ĐẠI TÍN HIỆU NHỎ
Khái niệm – Các đại lượng đặc trưng
Mô
hình
tín
hiệu
nhỏ
của
FET
–
số
mô
hình
2
Mô
hình
tín
hiệu
nhỏ
của
FET
–
số
mô
hình
Mô hình tín hiệu nhỏcủa BJT – Thông sốmô hình
Trong chương 4, ta đã xét mch khuch đi tín hiu ln, vO, vItuân theo qui
tc bo hoà, MOSFET ch trong vùng bo hoà.
H thc gia tín hiu ra – tín hiu vào cho:
là h thc không tuyn tính gia vIvà vO(H.6.1)
v
( )
2
2
I TH
O S L
v V
v V K R
−
= −
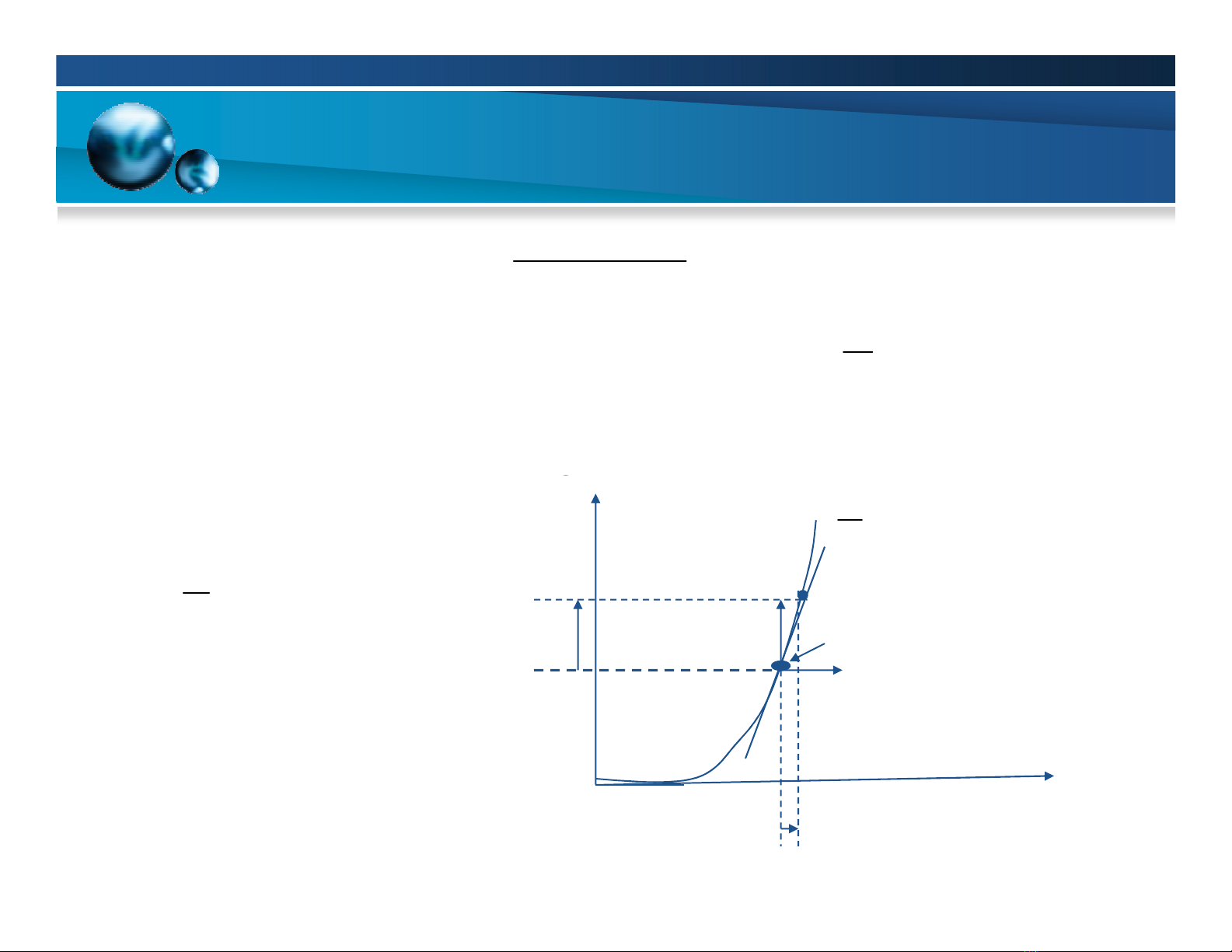
TỔNG QUAN
3
v
O
VS5V
vO= vI– VTH
vO1V vI
VTH 1V 2V vI
•Dưi dng:
•Vi thành phn DC và thành phn gia tăng:
•Đ th biu din: i
DS
( ) ( )
2
2
I TH
D D d I TH i
K V V
i I i K V V v
−
= + = + −
( )
( )
2
,
2
D I TH
d I TH i
K
I V V
i K V V v
= −
= −
TỔNG QUAN
DS
Nhn xét: iD Ids
Đim phân cc
ID Vgs
h s h dn gm = K(VGS – VTH)
Vá: VGS = VI
0 vTH VIvivGS
( )
2
2
GS TH
Kv V−
( )
( )
2
. .,
2
D I TH
d I TH i m i
K
I V V h s DCbias
i K V V v g v
= − =
= − =
•H thc không tuyn tính gây khó khăn cho vic phân tích và
thit lp mch khuch đi.
•Đ có mch khuch đi tuyn tính:
Phân cc DC đưc chn tt
đim hot đng trung đimvo
di hot đng ngõ vào
V
Đim hot đng
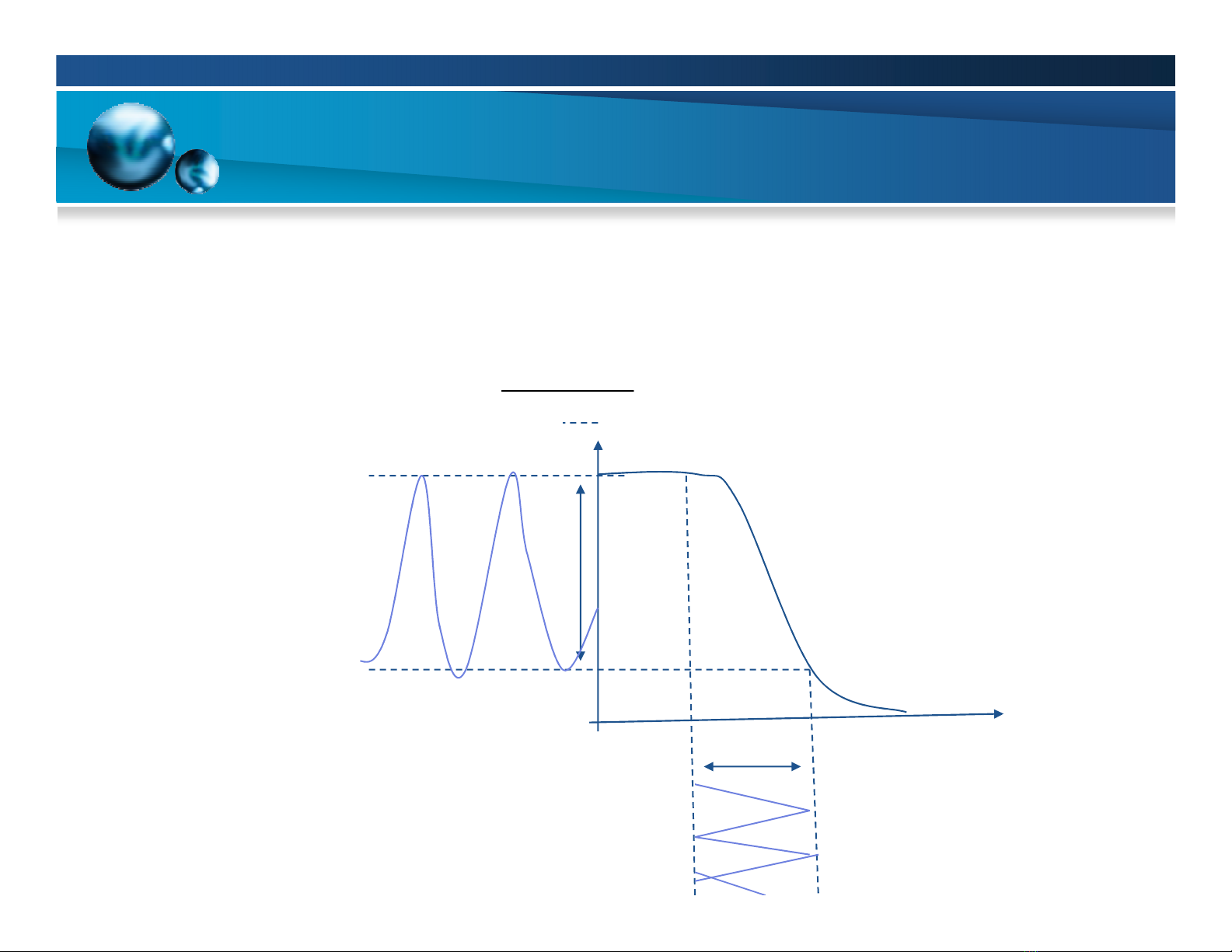
KHUẾCH ĐẠI TÍN HIỆU NHỎ
5
di hot đng ngõ vào
V
S
Đim hot đng
Đt chng tín hiu nh lên ( VI, VO)
phía trên ca VI.
Đáp ng ca tín hiu nh đưc
xem là gn như tuyn tính.
•Ta có th xét chi tit hơn bng:
- 1). Đ th
- 2). Toán hc
- 3). Nhìn t mch
O
v
∆
I
v
∆
VTH vI