
1
Lý thuyết đồ thị
Chương 1: Giới thiệu

2
Chương 1: Giới thiệu
Đ nh nghĩa:ị
Đ th (ồ ị graph) G = (V,E) là m t b g m 2 t p ộ ộ ồ ậ
h p các đ nh (ợ ỉ vertices) V (V≠Ø) và các c nh ạ
(edges) E. M i c nh t ng ng v i 2 đ nh. ỗ ạ ươ ứ ớ ỉ
N u c nh e t ng ng v i 2 đ nh v, w thì ta ế ạ ươ ứ ớ ỉ
nói v và w là 2 đ nh liên k t hay k (ỉ ế ề adjacent)
v i nhau và e đ c g i là t i các đ nh v, w. Ký ớ ượ ọ ớ ỉ
hi u ệ hay v w.
vwe
=
e
3
Chương 1: Giới thiệu
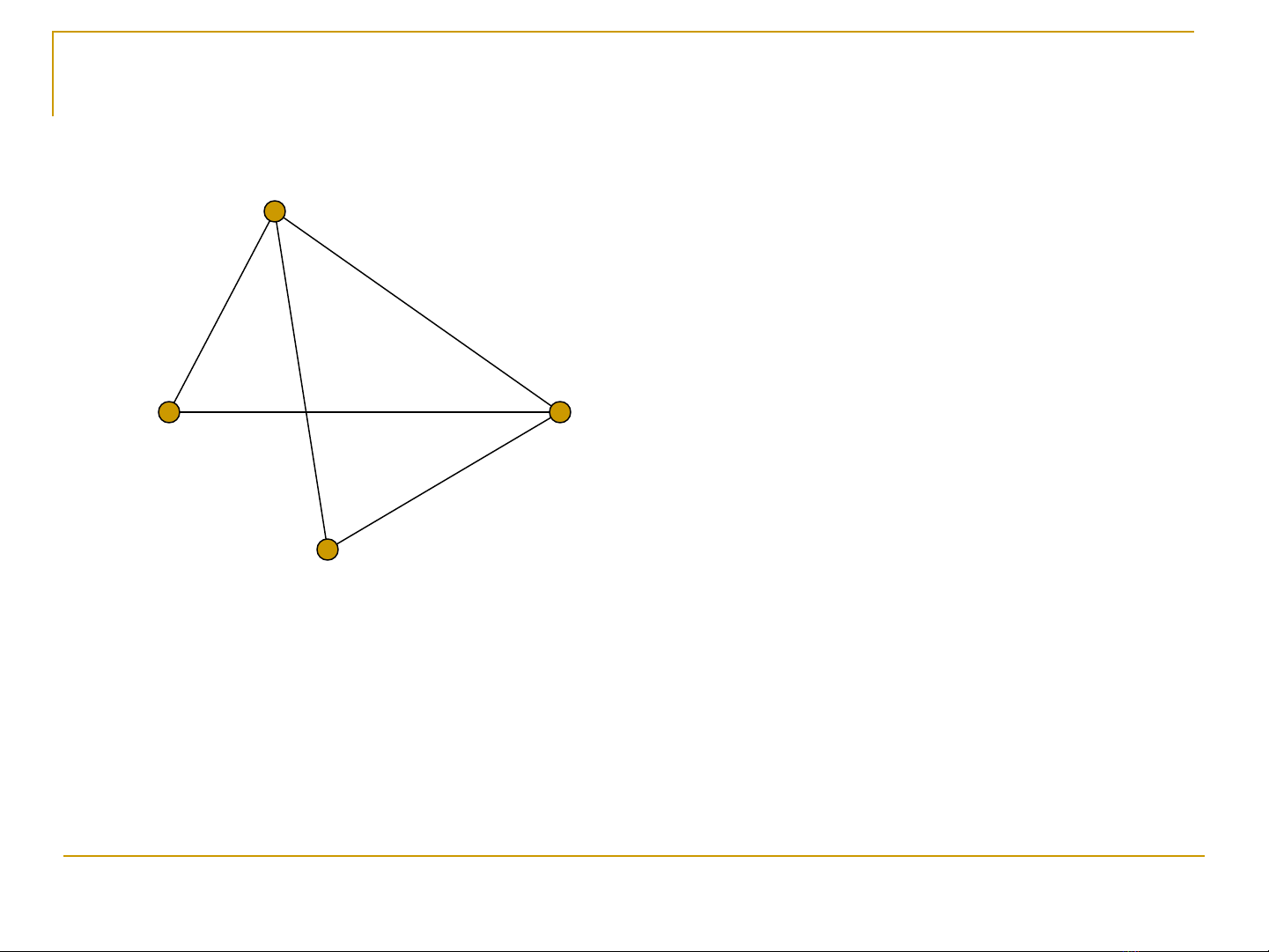
Các đ nh: A, B, C, Dỉ
Các c nh: AB, AC, AD, ạ
BD, BC
A
B
C
D
C nh không phân bi t th t c a đ nh đ c g i là ạ ệ ứ ự ủ ỉ ượ ọ
c nh vô h ng. Đ th bao g m các c nh vô ạ ướ ồ ị ồ ạ
h ng đ c g i là đ th vô h ng.ướ ượ ọ ồ ị ướ
4
Chương 1: Giới thiệu
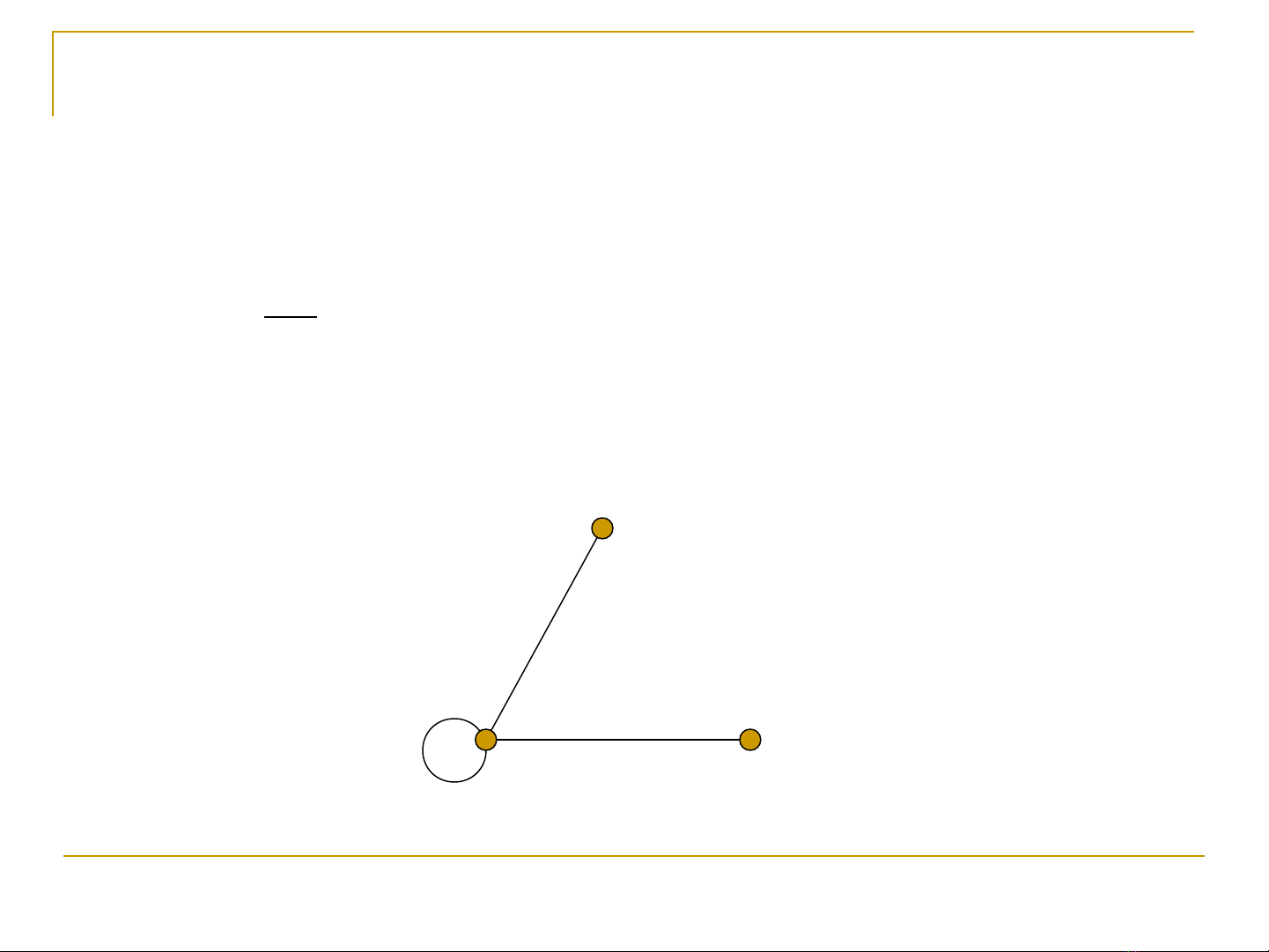
Đ nh nghĩa:ị
-C nh uv t ng ng v i 2 đ nh trùng nhau g i ạ ươ ứ ớ ỉ ọ
là vòng (loop) hay khuyên.
A
B
C
5
Chương 1: Giới thiệu
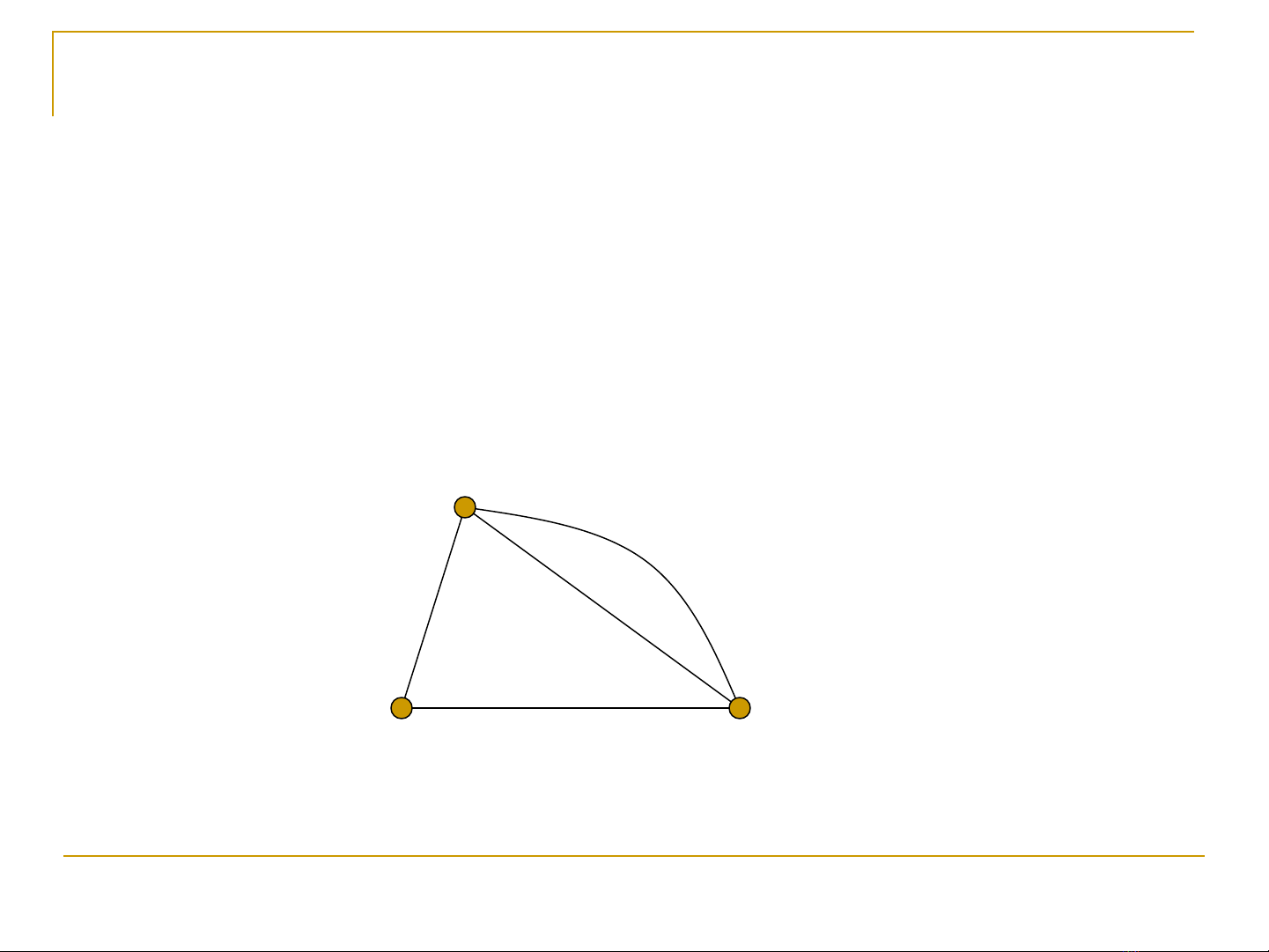
-Hai c nh phân bi t cùng t ng ng v i m t ạ ệ ươ ứ ớ ộ
c p đ nh g i là 2 c nh song song (ặ ỉ ọ ạ parallel
edge).
A
B
C











![Câu hỏi ôn tập Cấu trúc dữ liệu và giải thuật: Tổng hợp [mới nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251015/khanhchi0906/135x160/25431768554807.jpg)
![Bài giảng Thực hành cơ sở dữ liệu Trường ĐH Công Nghệ [năm] mới nhất](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251120/oursky02/135x160/14661768233842.jpg)













