Bài giảng: Mô hình máy điện hai chiều trong hệ tọa độ hai pha

Chia sẻ: Trần Văn Thắng | Ngày: | Loại File: PPT | Số trang:26

Thêm vào BST

Báo xấu

116
lượt xem 10
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng: Mô hình máy điện hai chiều trong hệ tọa độ hai pha, trình bày các nội dung chính: vì sao cần nghiên cứu mô hình máy điện xoay chiều trong hệ tọa độ hai pha, nhắc lại phương pháp kinh điển điều khiển động cơ xoay chiều không đồng bộ ba pha roto lồng sóc, tiệm cận phương pháp điều khiển vec tơ, xây dựng vec tơ không gian của các đại lượng ba pha, mô hình động cơ không đồng bộ ba pha trong hệ tọa độ từ trường roto,... Đây là tài liệu tham khảo dành cho sinh viên ngành Điện.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng: Mô hình máy điện hai chiều trong hệ tọa độ hai pha

Chuong 5. Mô hình máy điện xoay chiều trong hệ tọa độ hai pha Những nội dung nghiên cứu + Vì sao cần nghiên cứu mô hình máy điện xoay chiều trong hệ tọa độ hai pha. + Nhắc lại phương pháp kinh điển điều khiển động cơ xoay chiều không đồng bộ ba pha roto lồng sóc + Tiệm cận phương pháp điều khiển vec tơ + Xây dựng vec tơ không gian của các đại lượng ba pha + Mô hình động cơ không đồng bộ ba pha trong hệ tọa độ từ trường quay roto +Nguyên lý điều chế vec tơ không gian + Ứng dụng thực tiễn của phương pháp điều khiển vec tơ động cơ xoay chiều KĐB ba pha
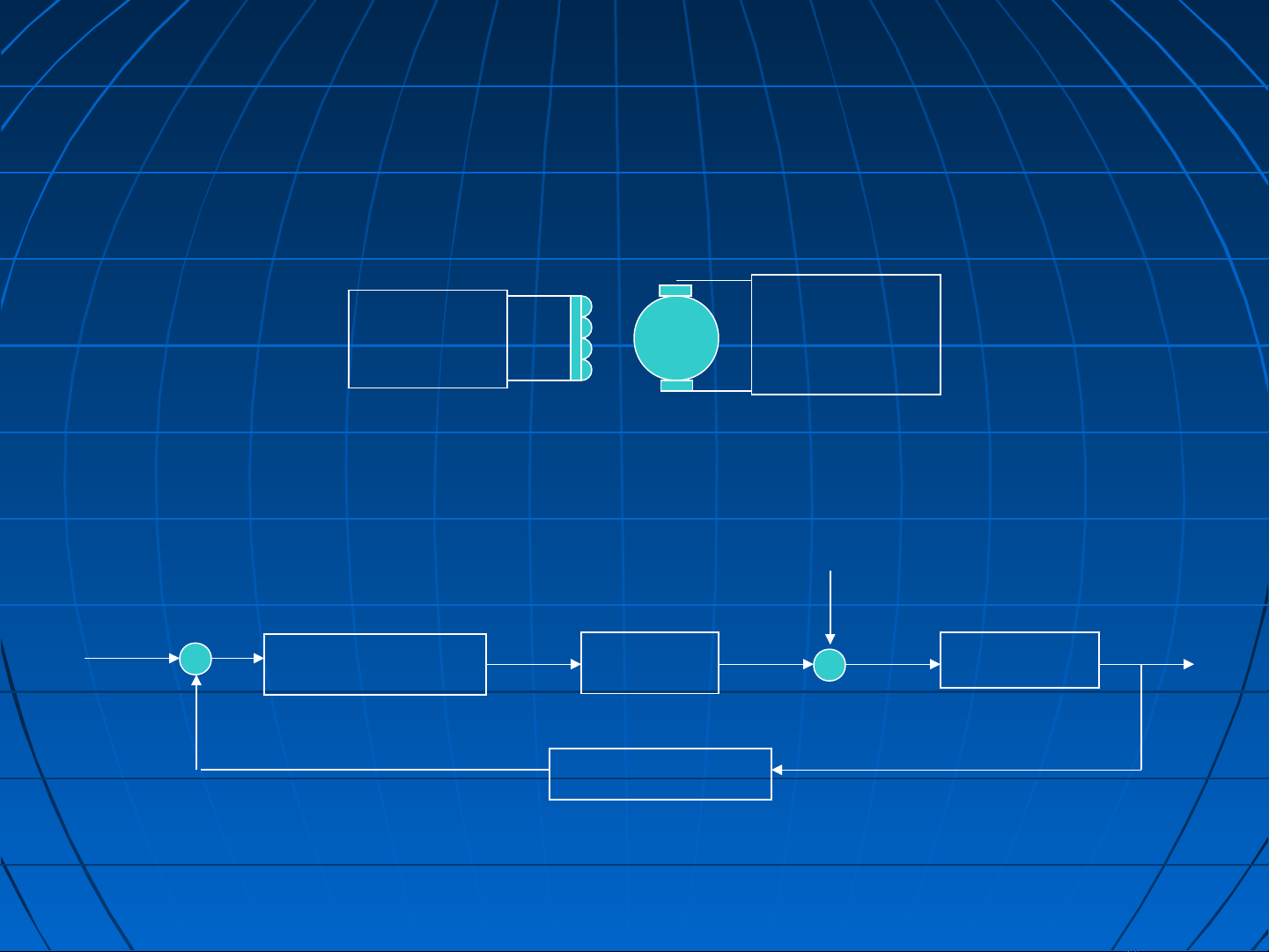
5.1: Vì sao cần nghiên cứu mô hình máy điện xoay chiều trong hệ tọa độ hai pha. 1. Mô hình máy điện một chiều kích từ độc lập Mô hình mạch Nguồn Nguồn KT PƯ 2. Mô hình động học MĐMC điều khiển ĐA phần ứng U=iư rư + Lưdiư/dt; M = CmiưФ; iưrư = UEư ; Eư= CmФ ω ; MMc = Jdω/dt Mc 1/(rư+pLư) Cm Ф 1/Jp Cm Ф
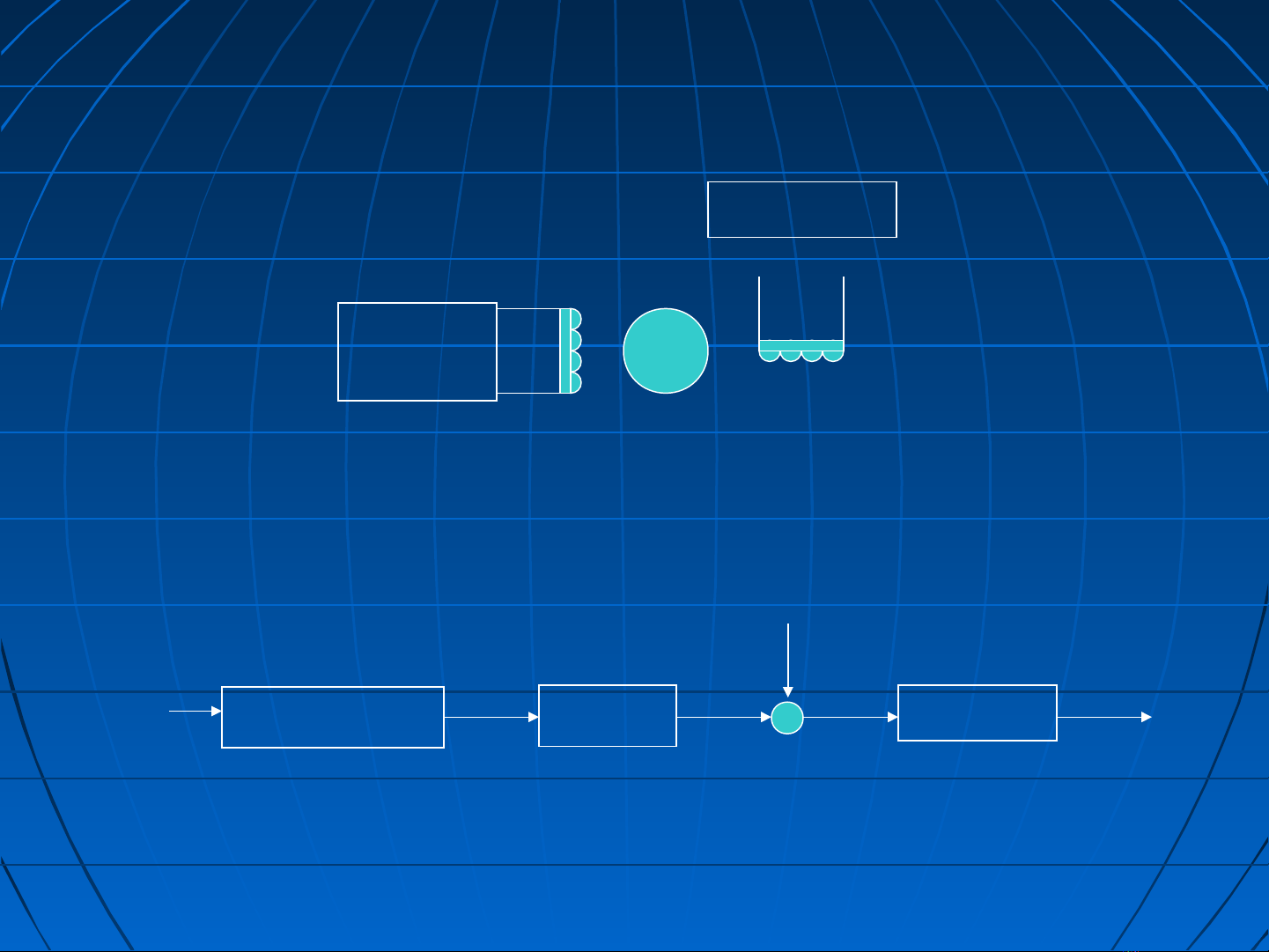
3. Mô hình máy điện XC hai pha Mô hình mạch Nguồn PƯ Nguồn ĐK 4. Mô hình động học MĐXC hai pha U=iư rư + Lưdiư/dt; M = CmiưIđk; MMc = Jdω/dt Mc 1/(rư+pLư) Cm Iđk 1/Jp Nhận xét: + Phương pháp điều khiển; mô hình
5.2 Phương pháp kinh điển điều khiển động cơ xoay chiều KĐBBP roto lồng sóc 1. Đặc điểm của động cơ không đồng bộ ba pha: + Không tách biệt dòng từ hóa (dòng kích thích) và dòng momen (dòng phần ứng). + Khi thay đổi điện áp hoặc dòng Stator sẽ làm cả hai thành phần dòng này thay đổi. Đây là nguyên nhân chính làm cho đặc tính của MĐKĐB có tính phi tuyến lớn; giải điều chỉnh hẹp; + Dòng từ hóa không khống chế có thể làm từ thông vượt quá giá trị cho phép gây quá tải mạch từ. Đây là nguyên nhân máy XC có khả năng quá tải kém máy một chiều. + Khả năng đổi chiều quay: kém linh động, gây đột biến tốc độ giữa hai chiều quay tại điểm đổi chiều
2. Các phương pháp ĐK tốc độ ĐCXCKĐB a. Điều khiển điện áp Stator b. Điều khiển điện kháng nối tiếp trong mạch Stator c. Điều khiển tần số f với các quy luật: U/f = const: Quy luật dự trữ momen không đổi Mmax/M = const. Bảo đảm từ thông không đổi U2/f = const : Quy luật giữ momen cực đại không đổi Điểm chung của các phương pháp điều khiển: Tác động vào mạch Stator, thay đổi giá trị hiệu dụng của điện áp hoặc dòng điện.
5.3: Tiệm cận cơ sở phương pháp vec tơ điều khiển ĐCĐXC ba pha 1. Biểu diễn một vec tơ trong mặt phẳng Trong tọa độ Đề các: V = ai + bj Trong hệ tọa độ cực: V = V θ Trong mặt phẳng phức: V = a + jb 2. Biểu diễn đại lượng điều hòa bằng số phức Một vec tơ V quay với tốc độ góc ω trong mp phức. Vec tơ được xác định bởi hai tham số: Modun vec tơ và tọa độ góc θ= ωt. Vec tơ biểu diến dưới dạng số phức: V = Vejθ = Vcos ωt+jVsin ωt Nhận xét thuần túy toán học: Muốn thay đổi các đại lượng điều hòa, ta thay đổi môdun hoặc vị trí của vec tơ. Thay đổi Modun liên quan tới biên độ; thay đổi vị trí liên quan tới tần số. Và ngược lai, muốn điều khiển vec tơ, ta thay đổi các thành phần (tọa độ) của nó.
Nhận xét: 1. Các đại lượng pha của MĐXCBP: ui , ii, ψi ( i chỉ số cuộn dây pha) là các đại lượng điều hòa. Liệu có thể tìm được một vec tơ (gọi là vec tơ tổng – vec tơ không gian) mà các giá trị tức thời trên các pha tại thời điểm quan sát là hình chiếu của vec tơ này trên các trục cuộn dây không? Nếu tìm và tổng hợp được một vec tơ như vậy, thay vì điều khiển giá trị hiệu dụng của các đại lượng pha, ta thực hiện điều khiển vec tơ này. 2. Nếu có vec tơ tổng như vậy, ta thực hiện điều chế vec tơ này trong hệ tọa độ hai pha, sau đó thực hiện chiếu (quy đổi) vec tơ này lên hệ tọa độ ba pha để xác định giá trị tưc thời của các đại lượng trong cuộn dây pha. Hai kết luận trên là cơ sở của phương pháp điều khiển vec tơ MĐXC ba pha.
5.4:Xây dựng vec tơ không gian của các đại lượng trong MĐXC ba pha 1. Xây dựng vec tơ không gian của các đại lượng MĐXC ba pha Ψc a. Nhắc lại vec tơ từ thông tổng Trong máy điện ba pha đối xứng, giả thiết Ψa biên độ từ thông mỗi pha không đổi: vec tơ từ thông tổng là tổng ba vec tơ từ thông tức thời của mỗi pha, có giá trị bằng 3/2Ψm; Ψb quay với tốc độ góc ω=2πf. + Từ sơ đồ vec tơ không gian của từ thông, ta thấy nếu chiếu vec tơ từ thông tổng lên các trục cuộn dây a, b, c sẽ được thành phần có độ lớn bằng 3/2 giá trị từ thông tức thời của mỗi pha. +Nếu ta lập vec tơ không gian, ψs (t) = 2/3[ψsa (t) + ψsb (t)+ ψsc(t)] Thì khi chiếu vec tơ này lên các trục cuộn dây, ta được chính giá trị tức thời của từ thông các pha đó tại thời điểm xem xét.
b. Xây dựng vec tơ không gian dòng ba pha isa isb isc pt cân bằng dòng ba pha isa + isb + isc = 0 Trong đó: isa = Imcosωst isb = Imcos(ωst1200) isc = Imcos(ωst2400) Trong không gian, trên mặt phẳng cắt ngang vuông góc với trục roto, ba cuộn dây stator lệch nhau một góc 1200. THiết lập hệ tọa độ phức với trục thực trùng trục cuộn dây pha a, vec tơ dòng điện tổng xây dựng theo công thức: is(t) = 2/3[isa(t) + isb(t)ej120 + isc(t)ej240] = is ejθs Θs = ωst là góc lệch của vec tơ tổng với trục thực; is(t) là vec tơ quay với tốc độ ωs=2πf. Giá trị tức thời của dòng điện trên mỗi pha chính là chiếu của vec tơ is(t) lên các trục pha a, b, c ( các tọa độ pha của vec tơ không gian)
 Minh họa trên hình vẽ vị trí vec tơ không gian tại Θ = ωst =600 b ic =is isa = Imcosωst = 1/2Im isb = Imcos(ωst1200)=1/2Im ib isc = Imcos(ωst2400)= Im ia a vị trí vec tơ không gian tại Θ = ωst =1200 isa = Imcosωst = 1/2Im c isb = Imcos(ωst1200)=Im c iscb =is mcos(ωst2400)= 1/2 Im I = I b b c ib ia Ia=is a Ib ic a Ic =is Ia Ic ωst =1200 ωst =1800 ωst =2400 c
2. Các thành phần của vec tơ không gian dòng stator trên hệ tọa độ hai pha (α,β). Thiết lập hệ toạ độ tĩnh gắn với stato, với trục α trùng trục thưc; β trùng trục ảo Các thành phần của vec tơ dòng trên trục α,β là isα và isβ. Hai dòng điện này là hình sin (chiếu vec tơ quay lên hệ trục cố định). Đây là phép chuyển dòng ba pha về dòng hai pha ( mô hình hai pha thay thế mô hình ba pha) Theo phép chiếu trên: isa = isα jβ isβ = 1/ 3 (isa + 2isb) isc pt trên cho phép xác định b is các thành phần của vec tơ dòng isβ stato trong hệ tọa độ 2 pha cố định từ các thành phần trong isb α hệ tọa độ ba pha. Isa=isα c
 Tương tự, ta biểu diễn các đại lượng khác trên hệ trục cố định (α,β). us = usα +jusβ Ψs = Ψsα +jΨsβ is = isα +jisβ Ψr = Ψrα +jΨrβ ir= irα +jirβ Các biểu thức trên là các đại lượng stator và roto quan sát trên hệ trục tọa độ cố định (α,β) ( hệ trục gắn với stator). *Ta tiếp tục nghiên cứu cách biểu diễn vec tơ trên hệ tọa độ quay để tiếp cận tới phép điều khiển vec tơ tựa từ trường quay rotor.
3. Các thành phần của vec tơ không gian dòng stator trên hệ tọa độ quay (d,q). a. Phép chuyển vị vec tơ giữa hai hệ trục tọa độ cố định Nếu có một hệ trục (x,y) lệch so với hệ trục (α,β) một góc θ Trên hệ (α,β): isαβ = isα +jisβ (1) jβ Trên hệ (x,y): isxy = isx +jisy (2) jy Isβ is x Quan hệ giữa chúng: Isx = isα cosθ + isβsinθ (3) isx isy θ Isy = isα sinθ + isβ cosθ (4) α Isa=isα Thay 3, 4 vào 2: isxy = isαβ (cosθ – jsinθ) = isαβejθ isαβ = isxy ejθ Nếu hệ trục (x,y) quay với tốc độ ωxy =dθ/dt các biểu thức 3,4 là phép quy đổi từ hệ tọa độ cố định sang hệ tọa độ quay.
b. Vec tơ không gian trong hệ tọa độ quay d,q * Hệ tọa độ quay (d,q) Gắn hệ trục (x,y) xét ở trên với trục từ thông rotor, ta có hệ tọa độ quay với tốc độ từ trường roto (ký hiệu f), với tốc dộ quay ωs =2πfs. Trên hệ (α,β): iss = isα +jisβ (5) jβ Trên hệ (d,q): i = isd +jisq (6) s f Quan hệ giữa chúng: jq Isβ is Trục Ψr d isd = isα cosθs + isβsinθs (7) isd isq = isα sinθs + isβ cosθs (8) isq θs isf = iss ejθs iss = isf e jθs Trục roto Isa=isα α θ Nếu biết θs, phép quy đổi từ hệ tọa độ cố định sang hệ tọa độ quay theo các biểu thức 7,8 . Điều kiện cần để thực hiện phép quy đổi là biết tốc độ góc ωs. Đây là nội dung cơ bản để thực hiện được phép điều khiển vec tơ tựa theo từ thông roto.
* Tương tự, ta có thể biểu diễn các vec tơ khác trên hệ tọa độ d,q usf = usd +jusq Ψsf = Ψsd +jΨsq Ψrf = Ψrd +jΨrq irf = ird +jirq Trong phương trình thứ 3, vì trục d vuông góc với q nên thành phần Ψrq= 0 Người ta quan niệm: Ψr = Ψrd do isd sinh ra (gọi là dòng từ thông – dòng kích từ): Ψrd = Lmisd /(1+pTr) isq là thành phần dòng momen: M=3/2*(Lm/Lr) *pc* Ψrd *isq • Hai biểu thức trên cho ta mo hình máy điện xoay chiều tương tự mô hình máy điện một chiều với momen phụ thuộc hai thành phần dòng kích từ và dòng phần ứng. • Nếu điều khiển giữ thành phần dòng kích từ không đổi, thì momen chỉ còn phụ thuộc dòng momen isq. Đây chính là nguyên tắc điều khiển MĐXC bằng phương pháp điều khiển vec tơ tựa từ thông rotor.
5.5 Mô hình động cơ KĐB roto lồng sóc trong hệ tọa độ hai pha  1. Ý nghĩa của việc xây dựng mô hình Muốn xây dựng hệ điều khiển một đối tượng, cần phải biết mô hình đối tượng. Mô hình đối tượng được xây dựng trên cơ sở HPT mô tả quá trình vật lý của đối tượng đó. Mô hình mạch của ĐCKĐB chúng ta đã xây dựng. Từ mô hình đó chúng ta đã biết các phương pháp điều khiển tốc độ động cơ trên cơ sở tác động vào mạch Stato. Ở đây chúng ta triếp cận tới một mô hình khác: mô hình động cơ trong hệ tọa độ hai pha tĩnh (α,β) và hệ tọa độ quay (d,q). Các giả thiết: Các cuộn dây phân bố đối xứng trong không gian Bỏ qua tổn hao sắt từ và bão hòa từ Nguồn xoay chiều 3 pha đối xứng
2. Hệ pt cơ bản của động cơ a. PT trong hệ tọa độ tĩnh Để thống nhất với các TL nước ngoài, ta ký hiệu 3 pha là u, v, w usu(t) = Rsisu(t)+dΨsu(t)/dt (1) usv(t) = Rsisv(t)+dΨsv(t)/dt (2) usw(t) = Rsisw(t)+dΨsw(t)/dt (3) * Ta xây dựng vec tơ không gian của điện áp stato us (t) = 2/3[usu(t)+usv(t)ej120+uswej240] (4) Thay 3 pt trên vào (4), ta có pt vector sau uss(t) = Rs iss(t) +dΨss (t)/dt (5) Đây là pt viết trong hệ tọa độ tĩnh stato nên ta thêm chỉ số “s” để phân biệt với hệ tọa độ quay * Tương tự, ta xây dựng pt vec tơ mạch roto trong hệ tọa độ roto 0= Rr ir +dΨr (t)/dt (6)
 Quan hệ giữa từ thông và dòng điện Ψs= Lsis + Lm ir (7) Lm: hỗ cảm giữa Stato và roto Ψr= Lmis + Lr ir (8) Ls; Lr : Điện cảm Stato và Roto • Phương trình momen M = 3/2 pc (Ψs x is) = 3/2(Ψr x ir) (9) • Phương trình cơ học M Mc = Jdω/dt (10) b. Phương trình điện áp Stato trong hệ tọa độ quay “k” uss = usk ejθk; iss = isk ejθk Ψss = Ψsk ejθk (11 a,b,c) θk là góc giữa trục thực của hệ tọa độ k so với trục thực α của hệ tọa độ tĩnh stato. Tốc độ góc của hệ k là ωk Đạo hàm 11©, ta được: dΨss /dt = dΨsk/dt.ejθk + jωkΨskejθk (11d) Thay 11 (a,b,d) vào 5 và biến đổi ta được pt tổng quát điện áp stato trong hệ toa độ k bất kỳ: usk = Rsisk + dΨsk/dt + jωkΨsk (12)
c. Pt điện áp stator trong hệ tọa độ quay (d,q) Từ (12) ta rút ra: nếu ωk= ωs, ta có pt điện áp stato trong hệ tọa độ quay (d,q) usf = Rsisf + dΨsf/dt + jωsΨsf (13) d. Pt điện áp rotor trong hệ tọa độ tĩnh (α,β) Thay ωk= ω ( coi stato quay ngược rotor) 0 = Rrirs+ dΨrs/dt jωΨrs (14) e. Pt điện áp rotor trong hệ tọa độ quay (d,q) 0 = Rrirf + dΨrf/dt + jωsΨrf (15) Các phương trình 7, 8, 13, 15 lập nên hệ phương trình động cơ mô tả trong hệ tọa độ quay (d,q). Từ các phương trình 7, 8, 12, 14 lập nên hệ phương trình động cơ mô tả trong hệ tọa độ tĩnh (α,β) ( thay ωk=0, thay chỉ số tọa độ f bằng chỉ số s)
3. Mô hình động cơ trên hệ tọa độ từ thông roto (d,q) Viết lại các pt 7, 8, 13, 15 Ψsf= Lsisf + Lm irf 16 Ψrf= Lmisf + Lr ir f 17 usf = Rsisf + dΨsf/dt + jωsΨsf 18 0 = Rrirf + dΨrf/dt + jωsΨrf 19 Từ 17: irf =1/Lr(Ψsf – Lm isf) 20 thế vào 16: Ψsf= Lσeisf + Lm/Lr Ψsf 21 Ls= Lm+Lσs; Lr= Lm+Lσr; Ts=Ls/Rs; Tr=Lr/Rr Lσe=(LsLrLm)/Lr Thay 20,21 vào 18,19 và chiếu hai vec tơ 18, 19 lên hai trục d,q ta được hpt máy ba pha trên hệ tọa độ từ thông roto. Lưu ý kết quả nhận được là do Ψrf= Ψr= Ψrd ; Ψrq=0. Bổ sung pt momen