intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng môn Cơ sở điều khiển tự động - Vũ Anh Đào

Chia sẻ: Na Na | Ngày: | Loại File: PDF | Số trang:99

Thêm vào BST
Báo xấu
272
lượt xem 58
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng môn Cơ sở điều khiển tự động trang bị cho các bạn những kiến thức cơ bản để phân tích và tổng hợp hệ thống điều khiển kỹ thuật trong miền thời gian và miền tần số bằng công cụ toán học, tập trung chủ yếu là các vấn đề trong miền liên tục. Mời các bạn tham khảo tài liệu để nắm bắt nội dung chi tiết.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng môn Cơ sở điều khiển tự động - Vũ Anh Đào

  1. HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG BÀI GIẢNG MÔN CƠ SỞ ĐIỀU KHIỂN TỰ ĐỘNG Giảng viên: Ths. Vũ Anh Đào Điện thoại/E-mail: anhdaoptit@gmail.com Bộ môn: Kỹ thuật điện tử Học kỳ/Năm biên soạn: 2009 Giới thiệu môn học • Mục đích: Trang bị cho sinh viên những kiến thức cơ bản để phân tích và tổng hợp hệ thống điều khiển kỹ thuật trong miền thời gian và miền tần số bằng công cụ toán học, tập trung chủ yếu là các vấn đề trong miền liên tục. Môn học thuộc lĩnh vực lý thuyết điều khiển, và là những cơ sở cơ bản nhất của lý thuyết hệ thống điều khiển được ứng dụng cho kỹ thuật. Các phương pháp được đề cập đến để phân tích và tổng hợp hệ thống là phương pháp kinh điển và phương pháp không gian trạng thái. Sinh viên được làm quen với phương pháp sử dụng phần mềm Matlab dùng để mô phỏng và tổng hợp hệ thống • Thời lượng: 3 đvht – Lý thuyết : 37 tiết – Kiểm tra : 2 tiết – Thí nghiệm: 6 tiết • Điểm thành phần: – Chuyên cần : 10% – Kiểm tra : 10% – Thí nghiệm : 10% – Thi kết thúc học phần: 70%
  2. Nội dung môn học PHẦN I. HỆ THỐNG ĐKTĐ TUYẾN TÍNH LIÊN TỤC Chương 1: Mô tả toán học hệ thống ĐKTĐ liên tục Chương 2: Đặc tính của các khâu cơ bản và của hệ thống ĐKTĐ liên tục Chương 3: Khảo sát tính ổn định của hệ thống ĐKTĐ liên tục Chương 4: Khảo sát chất lượng hệ thống ĐKTĐ liên tục Chương 5: Tổng hợp hệ thống ĐKTĐ liên tục PHẦN II. HỆ THỐNG ĐKTĐ TUYẾN TÍNH RỜI RẠC Chương 6: Mô tả toán học hệ thống ĐKTĐ rời rạc Chương 7: Phân tích và thiết kế hệ thống ĐKTĐ rời rạc Tài liệu tham khảo [1]. Vũ Anh Đào, Đặng Hoài Bắc, Bài giảng Cơ sở điều khiển tự động, HVCNBCVT, 2008. [2]. Phạm Công Ngô, Lý thuyết Điều khiển tự động, NXB KHKT, 2001 [3]. Nguyễn Văn Hoà, Cơ sở Lý thuyết điều khiển tự động, NXB KHKT, 2001. [4]. Nguyễn Thương Ngô, Lý thuyết Điều khiển tự động thông thường và hiện đại, NXB KHKT, 2005. [5]. Benjamin C. Kuo, Automatic Control Systems, Prentice - Hall International Editions, Seventh Edition 1995.
  3. Chương 1. Mô tả toán học hệ thống ĐKTĐ 1.1 Giới thiệu chung • ĐK học là khoa học nghiên cứu về các quá trình thu thập, xử lý tín hiệu và điều khiển trong mọi lĩnh vực đời sống xã hội, khoa học công nghệ, môi trường... • Điều khiển học kỹ thuật là khoa học nghiên cứu về quá trình thu thập, xử lý tín hiệu và điều khiển các quá trình và hệ thống thiết bị kỹ thuật. Khái niệm điều khiển được hiểu là tập hợp tất cả các tác động mang tính tổ chức của một quá trình nhằm đạt được mục đích mong muốn của quá trình đó. Hệ thống điều khiển mà không có sự tham gia trực tiếp của con người trong quá trình điều khiển được gọi là điều khiển tự động. 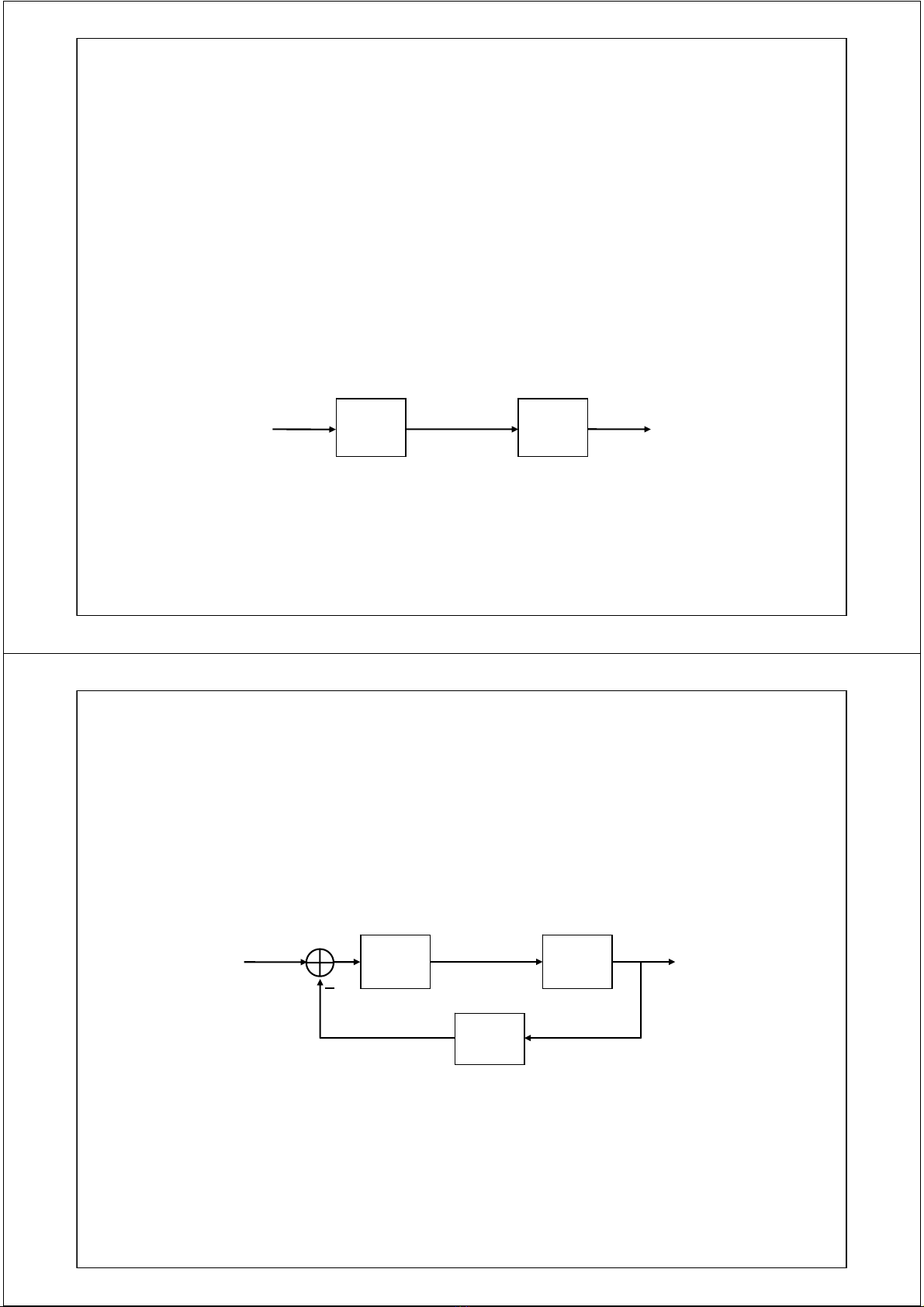• Một HTĐKTĐ hở (không có đường phản hồi) mô tả trong hình 1.1 gồm hai thành phần cơ bản là đối tượng điều khiển (Object) và thiết bị điều khiển (Controller): Tín hiệu vào Thiết bị Tín hiệu điều khiển Đối tượng Tín hiệu ra điều khiển điều khiển Hình 1.1 Hệ thống điều khiển hở • Nhiệm vụ cơ bản của điều khiển tạo ra tín hiệu điều khiển để có được giá trị đầu ra mong muốn. Những tác động từ bên ngoài lên hệ thống được gọi là tác động nhiễu 12/31/2009 Vũ Anh Đào - PTIT 5 Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.1.1 Sơ đồ khối • Hệ thống có đường phản hồi gọi là hệ kín, mô tả trong hình 1.2. f được gọi là tín hiệu phản hồi, e là sai lệch. Trong thực tế, các hệ thống điều khiển được sử dụng đều là các hệ kín, tức thông tin đầu ra được đưa quay trở về đầu vào để góp phần tạo ta tín hiệu điều khiển. Thiết bị Tín hiệu điều khiển Đối tượng Tín hiệu ra u e điều khiển x điều khiển y f Thiết bị đo Hình 1.2 Hệ thống điều khiển kín • Có ba phương thức điều khiển là phương thức điều khiển theo chương trình, phương thức bù nhiễu và phương thức điều khiển theo sai lệch (đây là phương pháp điều khiển phổ biến nhất) 12/31/2009 Vũ Anh Đào - PTIT 6
  4. Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.1.2 Phân loại hệ thống ĐKTĐ • Theo tính chất của các phần tử, HTĐKTĐ được phân làm 2 loại chính là hệ tuyến tính và hệ phi tuyến. – Hệ tuyến tính: tất cả các phần tử đều tuyến tính. – Hệ phi tuyến: có ít nhất 1 phần tử có tính phi tuyến. • Dựa vào tính chất truyền tín hiệu, HTĐKTĐ được phân làm 2 loại là hệ liên tục và hệ rời rạc (các khái niệm liên tục và rời rạc ở đây được hiểu theo biến thời gian). – Hệ liên tục: thông tin truyền đi liên tục ở tất cả các khâu. – Hệ rời rạc: thông tin truyền đi bị gián đoạn ở một khâu nào đó • Dựa vào lượng thông tin thu thập ban đầu về ĐTĐK và tính chất của nó, HTLTTT được phân ra làm 2 loại là hệ thông thường và hệ thích nghi – Hệ thông thường: cấu trúc và tham số của thiết bị điều khiển là không đổi với đối tượng điều khiển cụ thể – Hệ thích nghi: Khi đối tượng điều khiển có thông tin ban đầu không đầy đủ hay quá trình công nghệ có yêu cầu đặc biệt 12/31/2009 Vũ Anh Đào - PTIT 7 Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.2 Các phương pháp mô tả động học 1.2.1 Mô tả trong miền thời gian • Hàm truyền đạt: : là tỉ số giữa tín hiệu ra và tín hiệu vào theo biến đổi Laplace với điều kiện đầu triệt tiêu – Một HTĐKTĐ thường được biểu diễn dưới dạng PTVP dạng tổng quát: L { y ( t )} W ( p) = L {u ( t )} Biến đổi Laplace 2 vế, ta có hàm truyền đạt: dny d n−1 y dy d mu d m−1 y du a0 + a1 + ... + an−1 + an y = b0 m + b1 m−1 + … + bm−1 + bmu dt n dt n−1 dt dt dt dt Và phương trình đặc trưng: a0 p n + a1 p n−1 + ... + an−1 p + an = 0 – Nghiệm tử số của hàm truyền đạt được gọi là các điểm không (zero) và nghiệm mẫu số được gọi là các điểm cực (pole) 12/31/2009 Vũ Anh Đào - PTIT 8
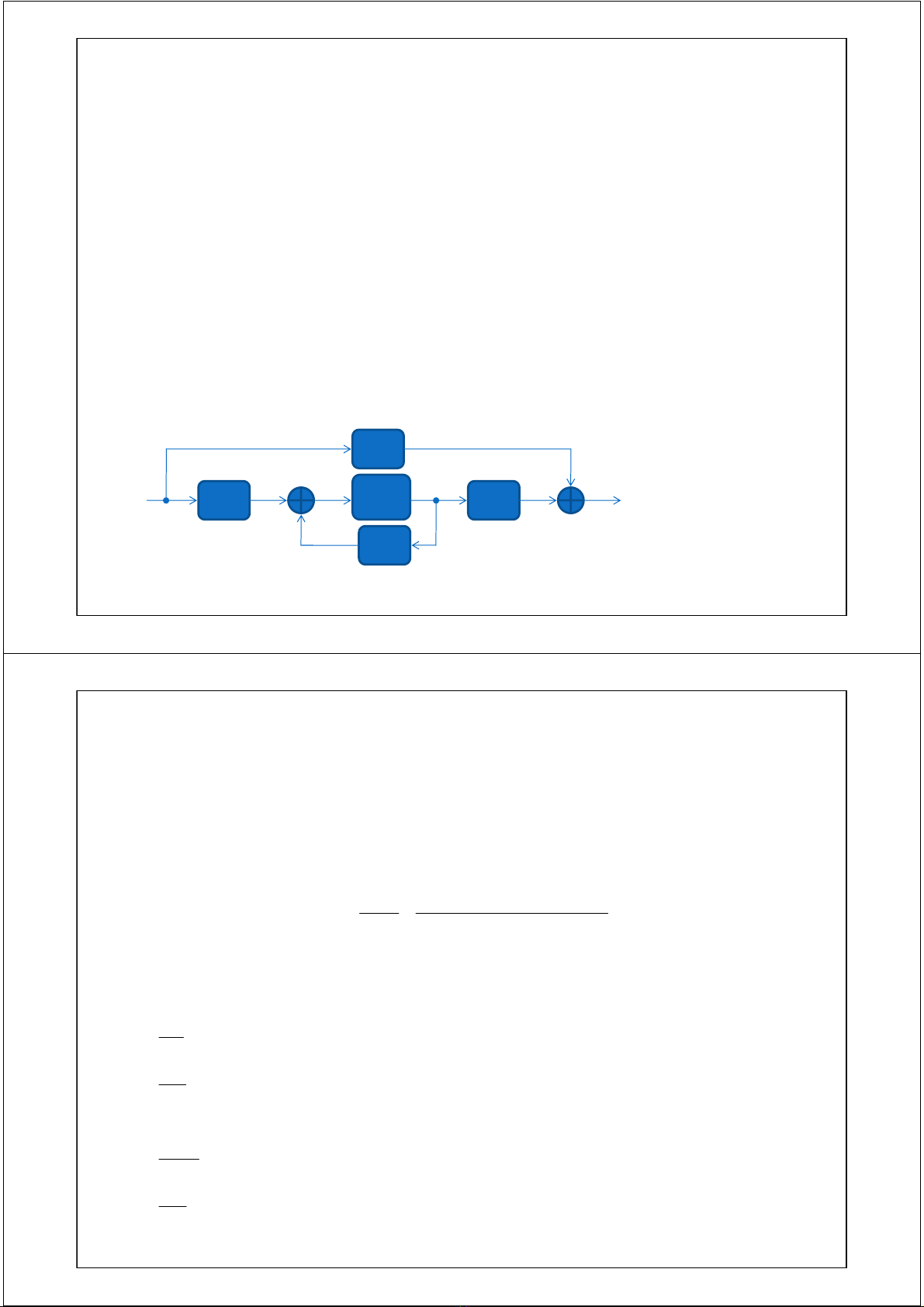
  5. Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Hệ phương trình không gian trạng thái ⎧ x = Ax + Bu ⎨ ⎩ y = Cx + Du ⎡ a11 a12 ... a1n ⎤ ⎡ b11 b12 ... b1r ⎤ ⎡ c11 c12 ... c1n ⎤ ⎡ d11 d12 ... d1r ⎤ ⎢a a ⎥ ... a2 n ⎥ ⎢b b ⎥ ... b2r ⎥ ⎢c c22 ⎥ ... c2n ⎥ ⎢d d 22 ... d 2r ⎥ A = ⎢ 21 22 , B = ⎢ 21 22 C = ⎢ 21 , D = ⎢ 21 ⎥ ⎢ ... ... ... ... ⎥ ⎢ ... ... ... ... ⎥ ⎢ ... ... ... ... ⎥ ⎢ ... ... ... ... ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ an1 an 2 ... ann ⎦ ⎣ bn1 bn 2 ... bnr ⎦ ⎣cm1 cm 2 ... cmn ⎦ ⎣ d m1 d m 2 ... d mr ⎦ x, dx/dt là các vector các biến trạng thái n chiều, u là vector tín hiệu vào r chiều, y là vector tín hiệu ra m chiều D u (t ) x (t ) x (t ) + y (t ) Hình 1.3 Sơ đồ cấu trúc + t B ∫ ( ) dτ o C trạng thái hệ liên tục + + A 12/31/2009 Vũ Anh Đào - PTIT 9 Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Chuyển từ hàm truyền đạt sang hệ phương trình trạng thái: – Nếu hệ thống có hàm truyền đạt dạng: Y ( p) K W ( p) = = U ( p) n p + A1 p n −1 + ... + An−1 p + An – Đặt: Ta có hệ PTTT: ⎧ x = Ax + Bu ⎨ ⎩ y = Cx + Du ⎧ y = x1 ⎪ dx ⎪ 1 = x2 − A1x1 ⎡ x1 ⎤ ⎡ 0 1 ... 0 ⎤ ⎡ x1 ⎤ ⎡ 0 ⎤ ⎢x ⎥ ⎢ 0 ⎥ ⎢x ⎥ ⎢ 0 ⎥ ⎪ dt ⎢ 2⎥ = ⎢ 0 ... 0 ⎥ ⎢ 2⎥ + ⎢ ⎥u ⎪ dx ⎢ ... ⎥ ⎢ ... ... ... ... ⎥ ⎢ ... ⎥ ⎢ ... ⎥ ⎪ 2 = x3 − A2 x1 ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎪ dt ⎣ xn ⎦ ⎣ − An − An −1 − A1 ⎦ ⎣ xn ⎦ ⎣ K ⎦ ⎨ ⎪... ⎡ x1 ⎤ ⎪ dxn−1 ⎢x ⎥ ⎪ = xn − An−1x1 ⎪ dt y ( t ) = [1 0 ... 0] ⎢ 2 ⎥ ⎢ ... ⎥ ⎪ dxn ⎢ ⎥ ⎪ dt = Ku − An x1 ⎩ ⎣ xn ⎦ 12/31/2009 Vũ Anh Đào - PTIT 10
  6. Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Trên cơ sở các phương trình trên, ta dễ dàng xây dựng mô hình hệ thống (hình 1.5) và sơ đồ cấu trúc trạng thái của hệ thống (hình 1.6) ⎧ y = x1 yn−1 y = y1 u y2 ⎪ dx k0 yn 1 yn 1 1 y2 y1 1 ⎪ 1 = x2 − A1x1 p p p p ⎪ dt ⎪ dx An−1 A2 A1 An ⎪ 2 = x3 − A2 x1 ⎪ dt ⎨ ⎪... ⎪ dxn−1 Hình 1.5 Mô hình hệ thống ⎪ = xn − An−1x1 + ⎪ dt u (t ) y y + y (t ) ⎪ dxn B t C ⎪ dt = Ku − An x1 ∫0 ( ) dτ ⎩ + ⎧ x = Ax + Bu A ⎨ ⎩ y = Cx + Du Hình 1.6 Sơ đồ cấu trúc trạng thái của hệ thống 12/31/2009 Vũ Anh Đào - PTIT 11 Chương 1. Mô tả toán học hệ thống ĐKTĐ... – Nếu hệ thống có hàm truyền đạt dạng: Y ( p ) B0 p m + B1 p m−1 + ... + Bm−1 p + Bm W ( p) = = U ( p) p n + A1 p n−1 + ... + An−1 p + An – Đặt: Ta có hệ PTTT: ⎧ x = Ax + Bu ⎨ ⎧ y = x1 ⎩ y = Cx + Du ⎪ dx ⎪ 1 = x2 − A1x1 + B0u ⎡ x1 ⎤ ⎡ − A1 1 ... 0 ⎤ ⎡ x1 ⎤ ⎡ B0 ⎤ ⎪ dt ⎢ x ⎥ ⎢ − A 0 ... ⎪ dx ⎢ 2⎥ = ⎢ 2 0 ⎥ ⎢ x2 ⎥ ⎢ B1 ⎥ ⎥⎢ ⎥ + ⎢ ⎥u ⎪ 2 = x3 − A2 x1 + B1u ⎢ ... ⎥ ⎢ ... ... ... ...⎥ ⎢ ... ⎥ ⎢ ... ⎥ ⎪ dt ⎨ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎪... ⎣ xn ⎦ ⎣ − An 0 ... 0 ⎦ ⎣ xn ⎦ ⎣ Bm ⎦ ⎪ dxn−1 ⎪ = xn − An−1x1 + Bm−1u ⎡ x1 ⎤ ⎢x ⎥ ⎪ dt ⎪ dxn y ( t ) = [1 0 ... 0] ⎢ 2 ⎥ ⎢ ... ⎥ ⎪ dt = Bmu − An x1 ⎩ ⎢ ⎥ ⎣ xn ⎦ 12/31/2009 Vũ Anh Đào - PTIT 12
  7. Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Chú ý: Hệ luôn phải thoả mãn điều kiện n-m=1 bằng cách thêm vào tử số các hệ số B0=0, B1=0… Trên cơ sở các phương trình trên, ta dễ dàng xây dựng mô hình hệ thống (hình 1.7) và sơ đồ cấu trúc trạng thái của hệ thống (hình 1.8) ⎧ y = x1 Bm−1 B1 B0 ⎪ dx ⎪ 1 = x2 − A1x1 + B0u ⎪ dt Bm yn 1 yn yn−1 1 y2 1 y1 1 y = y1 ⎪ dx u p p p p ⎪ 2 = x3 − A2 x1 + B1u ⎪ dt An An −1 A2 A1 ⎨ ⎪... ⎪ dxn−1 ⎪ = xn − An−1x1 + Bm−1u Hình 1.7. Mô hình hệ thống ⎪ dt + u (t ) y y (t ) ⎪ dxn B y t C + ⎪ dt = Bmu − An x1 ⎩ ∫0 ( ) dτ + ⎧ x = Ax + Bu A ⎨ ⎩ y = Cx + Du Hình 1.8. Sơ đồ cấu trúc trạng thái của hệ thống 12/31/2009 Vũ Anh Đào - PTIT 13 Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.2.2 Mô tả hệ thống trong miền tần số • Để xác định các đặc tính tần số của hệ thống, trước hết ta phải xác định được hàm truyền đạt tần số bằng cách thay p = jω vào hàm truyền đạt của hệ thống đã cho U Y U Y Wh ( p ) Wh ( p ) (a) (b) Hình 1.9 Sơ đồ hệ thống hở (a) và hệ thống kín (b) 1.2.2.1 Các đặc tính tần số của hệ hở Giả sử hệ thống hở được mô tả bởi hàm truyền đạt: Wh ( p ) = W1 ( p ) .W2 ( p ) ...Wn ( p ) Nếu hàm truyền tần số của các phần tử được mô tả dưới dạng: W jω = A ω .e i ( ) jϕ ω i ( ) i ( ) thì hàm truyền tần số của hệ hở được tính theo biểu thức: n n j ∑ ϕi ( ω ) 12/31/2009 Wh ( jω ) = ∏ Ai (ω ) .e i =1 Vũ Anh Đào - PTIT 14 i =1
  8. Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Các đặc tính tần số của hệ hở là: – Đặc tính biên tần (BT): n A (ω ) = ∏ Ai (ω ) i =1 – Đặc tính pha tần (hay pha tần logarithm – PT- PTL) n ϕ ( ω ) = ∑ ϕi ( ω ) i =1 – Đặc tính biên tần logarithm (BTL) n n L (ω ) = 20 lg A (ω ) = ∑ 20 lg Ai (ω ) = ∑ Li (ω ) i =1 i =1 – Như vậy, đặc tính BTL và PTL của hệ hở bằng tổng đại số của các đặc tính BTL và PTL của các phần tử thành phần. 12/31/2009 Vũ Anh Đào - PTIT 15 Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.2.2.2 Các đặc tính tần số của hệ kín • Hàm truyền đạt tần số của hệ kín là: A (ω ) e ( ) jϕ ω A (ω ) Wk ( jω ) = = jϕ (ω ) − jϕ (ω ) 1 + A (ω ) e e + A (ω ) • Sử dụng công thức Eurler: − jϕ (ω ) e = cos ϕ (ω ) − j sin ϕ (ω ) ta được: A (ω ) Wk ( jω ) = A (ω ) + cos ϕ (ω ) − j sin ϕ (ω ) • Tách phần thực và phần ảo, ta có: A (ω ) ⎡ A (ω ) + cos ϕ (ω ) ⎤ ⎣ ⎦ A (ω ) sin ϕ (ω ) Wk ( jω ) = +j 1 + A2 (ω ) + 2 cos ϕ (ω ) A (ω ) 1 + A2 (ω ) + 2 cos ϕ (ω ) A (ω ) 12/31/2009 Vũ Anh Đào - PTIT 16
  9. Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Các đặc tính tần số của hệ hở là: – Đặc tính biên tần (BT): A (ω ) Ak (ω ) = 1 + A2 (ω ) + 2 cos ϕ (ω ) A (ω ) – Đặc tính PT sin ϕ (ω ) ϕk (ω ) = arctg A (ω ) + cos ϕ (ω ) 12/31/2009 Vũ Anh Đào - PTIT 17 Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.3 Các nguyên tắc biến đổi sơ đồ khối 1.3.1 Hệ thống gồm các phần tử mắc nối tiếp • Các phần tử mắc nối tiếp nhau nếu tín hiệu ra của phần tử trước là tín hiệu vào của phần tử sau (hình 1.10) U U1 U2 Y U Y W1 W2 Wn W1.W2 ...Wn Hình 1.10 Sơ đồ hệ thống gồm các phần tử mắc nối tiếp • Từ hình 1.10 ta có: W1 = U1 U , W2 = U 2 U1 , Wn = Y U n−1 • Vậy hàm truyền đạt của hệ thống: Y W ( p) = = W1.W2 ...Wn U 12/31/2009 Vũ Anh Đào - PTIT 18
  10. Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.3.2 Hệ thống gồm các phần tử mắc song song • Các phần tử mắc song song nếu chúng có cùng tín hiệu vào, tín hiệu ra bằng tổng đại số của các tín hiệu ra thành phần(hình 1.11). • Từ hình 1.11, ta có: U1 = U W1 Y1 = W1U Y1 Y2 = W2U , ... U2 = U W2 Y2 Y U W1 + W2 + ... + Wn Y U Yn = WnU Yn Y = Y1 + Y2 + ... + Yn Un = U Wn • Hàm truyền đạt: Hình 1.11. Sơ đồ hệ thống gồm các phần tử mắc song song Y W ( p) = = W1 + W2 + ... + Wn U 12/31/2009 Vũ Anh Đào - PTIT 19 Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.3.3 Hệ thống gồm các phần tử mắc phản hồi (hồi tiếp) • Hệ thống có mạch mắc phản hồi gồm hai loại là phản hồi âm và phản hồi dương (hình 1.12). U E Y U E Y W1 W1 F F + W2 W2 (a) (b) Hình 1.12 Sơ đồ hệ thống có mạch phản hồi âm (a) và dương (b) – Hệ phản hồi âm (hình 1.12a) Hệ phản hồi dương (hình 1.12b): ⎧E = U − F ⎧E = U + F ⎪ Y W1 ⎨Y = W1E ⇒ W ( p ) = = ⎪ Y ⎨Y = W1E ⇒ W ( p ) = = W1 ⎪F = W Y U 1 + W1W2 ⎪F = W Y U 1 − W1W2 ⎩ 2 ⎩ 2 12/31/2009 Vũ Anh Đào - PTIT 20
  11. Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.3.4 Chuyển đổi vị trí các tín hiệu 1.3.4.1 Chuyển đổi tín hiệu vào • Từ trước ra sau một khối (hình 1.13): – Từ hình 1.13 (a): U1 U1 W Y Y = (U1 + U 2 )W U2 W Y U2 W – Từ hình 1.13 (b): (a) (b) Y = U1W + U 2W = (U1 + U 2 )W Hình 1.13 Chuyển tín hiệu vào từ trước ra sau một khối – Vậy tín hiệu chuyển từ trước ra sau một khối thì tín hiệu đó phải đi qua một khối mới có hàm truyền đạt chính bằng khối đó. 12/31/2009 Vũ Anh Đào - PTIT 21 Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Từ sau ra trước một khối (hình 1.14): – Từ hình 1.14 (a): U1 1W Y = U1 + U 2W U1 Y Y – Từ hình 1.14 (b): U 2 W U2 W Y = (U1. (1 W ) + U 2 )W (a) (b) = U1 + U 2W Hình 1.14 Chuyển tín hiệu vào từ sau ra trước một khối – Vậy tín hiệu chuyển từ sau ra trước một khối thì tín hiệu đó phải đi qua một khối mới có hàm truyền đạt chính bằng nghịch đảo của khối đó. 12/31/2009 Vũ Anh Đào - PTIT 22
  12. Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.3.4.1 Chuyển đổi tín hiệu ra • Từ trước ra sau một khối (hình 1.15): – Từ hình 1.15 (a): Y1 Y1 1W ⎧Y1 = U U W Y2 U W Y2 ⎨ ⎩Y2 = UW – Từ hình 1.15 (b): (a) (b) Hình 1.15 Chuyển tín hiệu ra từ trước ra sau một khối ⎪Y1 = UW (1 W ) = U ⎧ ⎨ ⎪Y2 = UW ⎩ – Vậy muốn chuyển tín hiệu ra từ trước ra sau một khối thì tín hiệu đó phải đi qua một khối mới có hàm truyền đạt chính bằng nghịch đảo của khối đó 12/31/2009 Vũ Anh Đào - PTIT 23 Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Từ sau ra trước một khối (hình 1.16): Y1 – Từ hình 1.16 (a): Y1 W ⎧Y1 = UW Y2 ⎨ U U W Y2 W ⎩Y2 = UW – Từ hình 1.16 (b): (a) (b) ⎧Y1 = UW ⎨ Hình 1.16 Chuyển tín hiệu ra từ sau ra trước một khối ⎩Y2 = UW – Vậy muốn chuyển tín hiệu ra từ sau ra trước một khối thì tín hiệu đó phải đi qua một khối mới có hàm truyền đạt chính bằng chính khối đó 1.3.4.3 Các bộ cộng liền nhau có thể đổi chỗ cho nhau (hình 1.17) Y Y U1 U1 U2 U3 Hình 1.17 U3 U2 (a) (b) 12/31/2009 Vũ Anh Đào - PTIT 24
  13. Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Ví dụ 1.1. Xác định hàm truyền đạt của hệ thống có sơ đồ như hình 1.18: – Cách 1: Chuyển A về B (chuyển tín hiệu ra từ sau ra trước khối W3), sau đó hoán đổi vị trí của A và B. – Cách 2: Chuyển B về A (chuyển tín hiệu ra từ trước ra sau khối W3), sau đó hoán đổi vị trí của A và B. W6 + U + B Y W1 W2 W3 W4 A W5 Hình 1.18 12/31/2009 Vũ Anh Đào - PTIT 25 Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Theo cách 1, hệ thống tương đương hình 1.19. W2 W236 = W6 W3 1 − W2 .W3 .W6 • Từ hình 1.20: + U + B Y W1 W2 W3 W4 W1.W236 A’ W12356 = 1 + W5.W1.W236 W5 • Hàm truyền đạt hở: Wh = W12356 .W3 .W4 Hình 1.19 U B Y • Hàm truyền đạt kín: W1 W236 W3 W4 Wh Wk = 1 + Wh W5 W12356 .W3 .W4 = 1 + W12356 .W3 .W4 12/31/2009 Vũ Anh Đào - PTIT Hình 1.20 26
  14. Chương 1. Mô tả toán học hệ thống ĐKTĐ... 1.4 Graph tín hiệu • Ở các nhánh của Graph đánh dấu mũi tên và hàm truyền tương ứng. Ở các nút của Graph đánh dấu mối liên hệ giữa các phần tử. • Graph được dùng để xác định hàm truyền đạt của hệ thống điều khiển tự động với các đặc điểm sau: – Graph là đồ hình gồm các nhánh và các nút. – Mỗi một nút của graph được biểu diễn bằng một điểm và ghi tên một đại lượng nào đó. Nút gốc là lượng vào, nút ngọn là lượng ra. – Một nhánh nối nút gốc và nút ngọn có mũi tên, trên đó ghi giá trị hàm truyền đạt tương ứng với một khâu nào đó (hình 1.21). Hàm truyền đạt của một nhánh bằng tỉ số giữa giá trị nút ngọn và giá trị nút gốc: yi aij yj aij = y j yi Hình 1.21 Các biểu hiện nhánh và nút của Graph 12/31/2009 Vũ Anh Đào - PTIT 27 Chương 1. Mô tả toán học hệ thống ĐKTĐ... • Các tính chất quan trọng của Graph tín hiệu: – Graph tín hiệu chỉ sử dụng cho các hệ thống tuyến tính. – Các phương trình dùng để vẽ Graph phải là các phương trình đại số. – Các nút được dùng để biểu thị các biến. Thông thường các nút được sắp xếp từ trái qua phải, từ đầu vào đến đầu ra. – Trong nhánh, các tín hiệu chỉ đi theo hướng mũi tên. – Nhánh hướng từ nút đến biểu diễn sự phụ thuộc của vào chứ không có chiều ngược lại. – Tín hiệu đi qua nhánh từ đến sẽ được nhân với hệ số khuếch đại của nhánh, . • Ví dụ 1.2. Dùng Graph biểu diễn hệ phương trình sau: ⎧ y2 = a12 y1 + a32 y3 ⎪ ⎪ y3 = a23 y2 + a43 y4 ⎨ ⎪ y4 = a24 y2 + a34 y3 + a44 y4 ⎪ y5 = a25 y2 + a45 y4 ⎩ 12/31/2009 Vũ Anh Đào - PTIT 28
  15. a32 a12 y1 y2 y3 y4 y5 a. y2 = a12 y1 + a32 y3 a32 a43 a12 a23 y1 y2 y3 y4 y5 y2 = a12 y1 + a32 y3 b. a44 y3 = a23 y2 + a43 y4 a32 a43 a12 a23 a34 y1 y2 y3 y4 y5 a24 y2 = a12 y1 + a32 y3 c. y3 = a23 y2 + a43 y4 y4 = a24 y2 + a34 y3 + a44 y4 a44 a32 a43 a12 a23 a34 a45 y1 y2 y3 y4 y5 a24 a25 y2 = a12 y1 + a32 y3 y3 = a23 y2 + a43 y4 d. y4 = a24 y2 + a34 y3 + a44 y4 12/31/2009 y5 = a25 y2 + a45 y4 Vũ Anh Đào - PTIT 29 ì Cá ớ â G í iệ í Chương 1. Mô tả toán học hệ thống ĐKTĐ... a2 a1 y1 y2 a1 + a2 + a3 a3 Hình 1.23. Graph của nhánh mắc song song y1 y2 y3 y4 y1 y4 a1 a2 a3 a1.a2 .a3 Hình 1.24 Graph của nhánh mắc nối tiếp a1 y1 y2 y1 y2 a1 1 + a1a2 − a2 Hình 1.25. Graph của nhánh mắc phản hồi 12/31/2009 Vũ Anh Đào - PTIT 30
  16. Chương 2. Các đặc tính của hệ liên tục 2.1 Giới thiệu chung • Có hai loại tín hiệu bên ngoài tác động và hệ thống, đó là tín hiệu đặt trước và nhiễu. Trong các HTĐK, tín hiệu đặt trước thường là một hằng số. • Nhiễu sẽ làm cho đầu ra của hệ thống bị lệch khỏi giá trị mong muốn. Nó có thể là những đột biến tăng (đường 1) hay giảm (đường 2), có thể theo một đường nhất định (tiền định) (đường 3) hay ngẫu nhiên (đường 4 – hình 2.1). • Dựa vào miền làm việc của tín hiệu thì HTĐKTĐ có hai đặc tính cơ bản là đặc tính thời gian và đặc tính tần số. Dựa vào đặc tính của hệ thống thì ta có đặc tính động (đặc trưng cho quá trình quá độ ) và đặc tính tĩnh (đặc trưng cho quá trình xác lập). x(t) 3 1 2 4 t Hình 2.1 12/31/2009 Vũ Anh Đào - PTIT 1 Chương 2. Các đặc tính của hệ liên tục… 2.2 Đặc tính thời gian của hệ thống • Khi phân tích một HT, ta thường dùng tín hiệu chuẩn làm tín hiệu vào, đặc tính của hệ thống được đánh giá bằng cách nghiên cứu đáp ứng của hệ thống trong miền thời gian. Việc đánh giá cuối cùng các đặc tính của HTĐK là dựa vào các đáp ứng thời gian. • Đáp ứng thời gian thường được chia thành hai phần là đáp ứng ở trạng thái quá độ và đáp ứng ở trạng thái xác lập. Ký hiệu y(t) là đáp ứng của một hệ thống liên tục thì ta có thể viết: y ( t ) = yqd ( t ) + y xl ( t ) trong đó yqd(t) là đáp ứng ở trạng thái quá độ và yxl(t) là đáp ứng ở trạng thái xác lập. • Đáp ứng quá độ là phần đáp ứng thời gian mà nó tiến tới 0 sau một khoảng thời gian rất lớn: lim y t = 0 qd () t →∞ • Đáp ứng xác lập là phần đáp ứng thời gian sau khi quá trình quá độ kết thúc. Đáp ứng xác lập vẫn có thể thay đổi trong những trường hợp cố định, ví dụ như khi đầu vào là sóng sin, hàm dốc tăng theo thời gian. 12/31/2009 Vũ Anh Đào - PTIT 2
  17. Chương 2. Các đặc tính của hệ liên tục… • Để đơn giản khi xét tính chất của một hệ thống, ta thường chia nhỏ nó thành các phần tử. Đặc tính thời gian của phần tử là sự thay đổi của phần tử theo thời gian khi tác động ở đầu vào là những tín hiệu chuẩn. Các đặc tính đó bao gồm hàm quá độ, đường quá độ, hàm quá độ xung và đường quá độ xung. Tín hiệu vào Tín hiệu ra Phần tử y x Hình 2.2 Mô hình biểu diễn phần tử • Các hàm thời gian này đều mô tả sự biến thiên của tín hiệu ra khi phần tử chuyển từ trạng thái cân bằng này sang trạng thái cân bằng khác do sự tác động của một trong các nhiễu chuẩn. Để đơn giản, ta xét trạng thái cân bằng ban đầu của các phần tử là không ( y(0)=0) 12/31/2009 Vũ Anh Đào - PTIT 3 Chương 2. Các đặc tính của hệ liên tục… 2.2.1 Tín hiệu tác động ở đầu vào • Tín hiệu bậc thang đơn vị 1(t): δ (t ) 1( t ) ⎧0 khi t ≤ 0 1( t ) = ⎨ 1 ⎩1 khi t > 0 • Tín hiệu xung đơn vị δ(t): 0 t 0 t d ⎧0 khi t ≠ 0 (a) (b) δ ( t ) = 1( t ) = ⎨ 1( t ) 1( t ) dt ⎩∞ khi t = 0 – Hàm δ(t) có tính chất: y ( t ) = atx ( t ) y ( t ) = at 2 x ( t ) ∞ ∫−∞ δ ( t ) = 1 0 t 0 t (c) (d) • Tín hiệu tuyến tính: Hình 2.3. (a). Đồ thị hàm 1( t ) ; (b). Đồ thị hàm δ ( t ) y ( t ) = atu ( t ) c. Hàm tuyến tính; d. Hàm parabol trong đó là hằng số thực. 12/31/2009 Vũ Anh Đào - PTIT 4
  18. Chương 2. Các đặc tính của hệ liên tục… • Hàm parabol: y ( t ) = at 2 x ( t ) trong đó là hằng số thực • Tín hiệu có dạng bất kỳ x(t): có thể được mô tả thông qua hàm 1(t) và δ(t): – Biểu diễn x(t) qua hàm 1(t): dựa vào tích phân Duyamen (khi α→0): dx (τ ) t x ( t ) = x (α ) .1( t ) + ∫ 0 dτ .1( t − τ ) dτ – Biểu diễn x(t) qua hàm δ(t): (khi α→0): t +α x (t ) = ∫α x (τ ) .δ ( t − τ ) dτ 12/31/2009 Vũ Anh Đào - PTIT 5 Chương 2. Các đặc tính của hệ liên tục… 2.2.2 Phản ứng của phần tử • Hàm quá độ h(t): là phản ứng của phần tử khi đầu vào là hàm 1(t). Nếu x ( t ) = 1( t ) thì L ⎡1( t ) ⎤ = 1 p ⎣ ⎦ Mối liên hệ giữa hàm truyền đạt và hàm quá độ của phần tử là: L ( h (t )) W ( p) W ( p) = = p.L ⎡ h ( t ) ⎤ ⇒ ⎣ ⎦ L ⎡h ( t )⎤ = ⎣ ⎦ L (1( t ) ) p • Đường quá độ: Được ký hiệu là H(t), là phản ứng của phần tử khi tín hiệu tác động ở đầu vào là nhiễu bậc thang có biên độ bằng A dạng A.1(t). Dựa vào nguyên lý xếp chồng của phần tử tuyến tính: AW ( p ) . H ( t ) = A.h ( t ) ⇒ L ( H ( t ) ) = p 12/31/2009 Vũ Anh Đào - PTIT 6
  19. Chương 2. Các đặc tính của hệ liên tục… • Hàm quá độ xung (hàm trọng lượng) k(t): là phản ứng của phần tử khi đầu vào là hàm δ(t). L ⎡δ ( t ) ⎤ = 1 ⇒ L ⎡ k ( t ) ⎤ = W ( p ) ⎣ ⎦ ⎣ ⎦ • Đường quá độ xung K(t):là phản ứng của phần tử khi đầu vào là hàm A.δ(t) Theo tính chất của δ(t) ta có thể viết: t t ∫0 x ( t ) = x ( t ) . δ ( t − τ ) .dτ = ∫0 x (τ )δ ( t − τ ).dτ Trong đó x(τ) là giá trị hàm x(t) tại thời điểm t= τ và δ(t-τ) là giá trị hàm δ(t) được phát tại thời điểm t= τ . Theo nguyên lý xếp chồng, ta có thể xác định đáp ứng y(t) của phần tử: t y (t ) = ∫0 x (τ ) k ( t − τ ) .dτ 12/31/2009 Vũ Anh Đào - PTIT 7 Chương 2. Các đặc tính của hệ liên tục… • Mối liên hệ giữa hàm quá độ h(t) và hàm trọng lượng k(t): W ( p) Ta nhận thấy L ⎡ h ( t ) ⎤ = ⎣ ⎦ và L ⎡ k ( t ) ⎤ = W ( p ) ⎣ ⎦ p Vì L ⎧ dh ⎫ ⎨ ⎬ = p.L {h ( t )} . ⎩ dt ⎭ Vậy: k (t ) = h '(t ) 12/31/2009 Vũ Anh Đào - PTIT 8
  20. Chương 2. Các đặc tính của hệ liên tục… 2.3 Đặc tính tần số của hệ thống • Đặc tính tần số của phần tử mô tả mối liên hệ giữa tín hiệu ra và tín hiệu vào của phần tử ở trạng thái xác lập khi thay đổi tần số dao động điều hòa tác động ở đầu vào của phần tử. • Muốn tìm các đặc tính tần số của hệ thống, trước hết ta phải tìm hàm truyền đạt tần số của hệ thống bằng cách thay p=jω vào hàm truyền đạt của nó m m−1 Ar jϕ(ω) b0.( jω) +b .( jω) +... +bm−1. jω+bm W( jω) A (ω ) = A A = = e 1 A r v a0.( jω)n +a1.( jω)n−1 +... + an−1. jω+ an v • Tách riêng phần thực, phần ảo của tử số và mẫu số trong (2.29) ta được: R (ω ) + jI1 (ω ) W ( jω ) = A (ω ) .e ( ) = 1 jϕ ω R2 (ω ) + jI 2 (ω ) Trong đó A (ω ) = Ar Av là đặc tính biên tần của phần tử; R1 (ω ) , R2 (ω ) là đặc tính phần thực của tử số và mẫu số; I1 (ω ) , I 2 (ω ) là đặc tính phần ảo của tử số và mẫu số 12/31/2009 Vũ Anh Đào - PTIT 9 Chương 2. Các đặc tính của hệ liên tục… • Tách phần thực và phần ảo của biểu thức trên ta được: R (ω ) .R2 (ω ) + I1 (ω ) .I 2 (ω ) R (ω ) .I1 (ω ) − R1 (ω ) .I 2 (ω ) A (ω ) .e ( ) = 1 jϕ ω +j 2 R2 (ω ) + I 2 (ω ) 2 2 R2 (ω ) + I 2 (ω ) 2 2 • Đặc tính phần thực của phần tử: R1 (ω ) .R2 (ω ) + I1 (ω ) .I 2 (ω ) R (ω ) = R2 (ω ) + I 2 (ω ) 2 2 • Đặc tính phần ảo của phần tử: R2 (ω ) .I1 (ω ) − R1 (ω ) .I 2 (ω ) I (ω ) = R2 (ω ) + I 2 (ω ) 2 2 • Ta nhận thấy R(ω) là hàm chẵn, nghĩa là R(ω) = R(-ω); còn I(ω) là hàm lẻ, nghĩa là I(ω) = -R(-ω) 12/31/2009 Vũ Anh Đào - PTIT 10
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí
65 tài liệu
2431 lượt tải
THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
2=>2