Bài giảng môn Kỹ thuật điện – Chương 3: Các phương pháp giải mạch điện

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:18

Thêm vào BST

Báo xấu

44
lượt xem 5
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng môn Kỹ thuật điện – Chương 3: Các phương pháp giải mạch điện gồm có những nội dung chính sau: Phương pháp dòng điện nhánh, phương pháp dòng điện vòng, phương pháp điện áp 2 nút, phương pháp biến đổi tổng trở tương đương. Mời các bạn cùng tham khảo.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng môn Kỹ thuật điện – Chương 3: Các phương pháp giải mạch điện

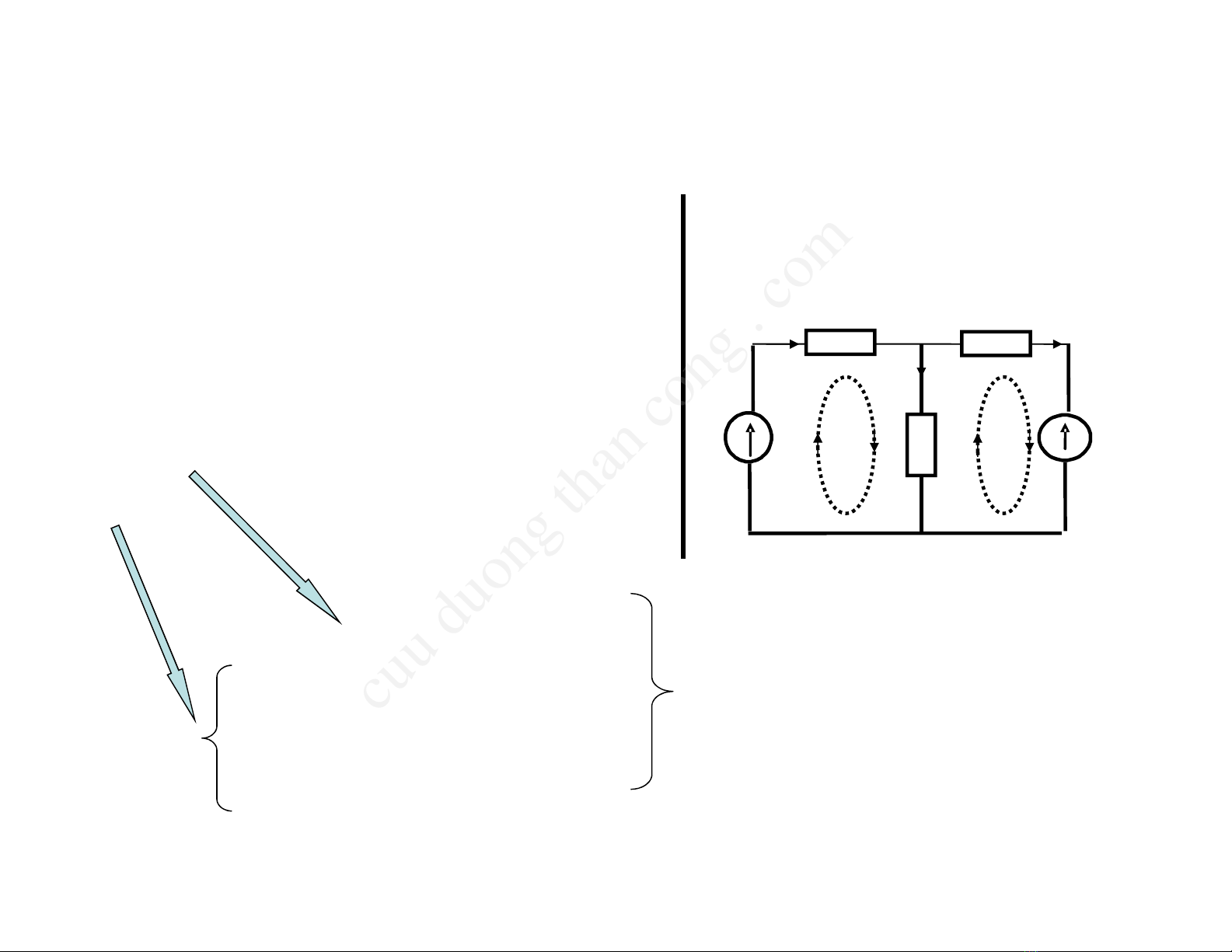
Chương III: CÁC PHƯƠNG PHÁP GIẢI MẠCH ĐIỆN 3.1 : Phương pháp dòng điện nhánh VD: om - Chọn dòng trong các nhánh làm ẩn .c I11 Z 1 Z3 I3 3 Mạch điện có m nhánh, n nút ng 2I2 => có m ẩn => Cần m PT co E1 V1 Z 2 V2 E3 Theo K1 : n - 1 pt an th Theo K2 : m-n+1 pt : ng o i i i I1− I 2 − I3 = 0 du i Biết Zk ,Ek u i i i cu V1 Z1 I1 + Z2 I2 = E1 giải hệ 3 PT i i i i i i V2 −Z2 I2 + Z3 I3 = − E3 => tìm I1 , I 2 , I 3 CuuDuongThanCong.com https://fb.com/tailieudientucntt
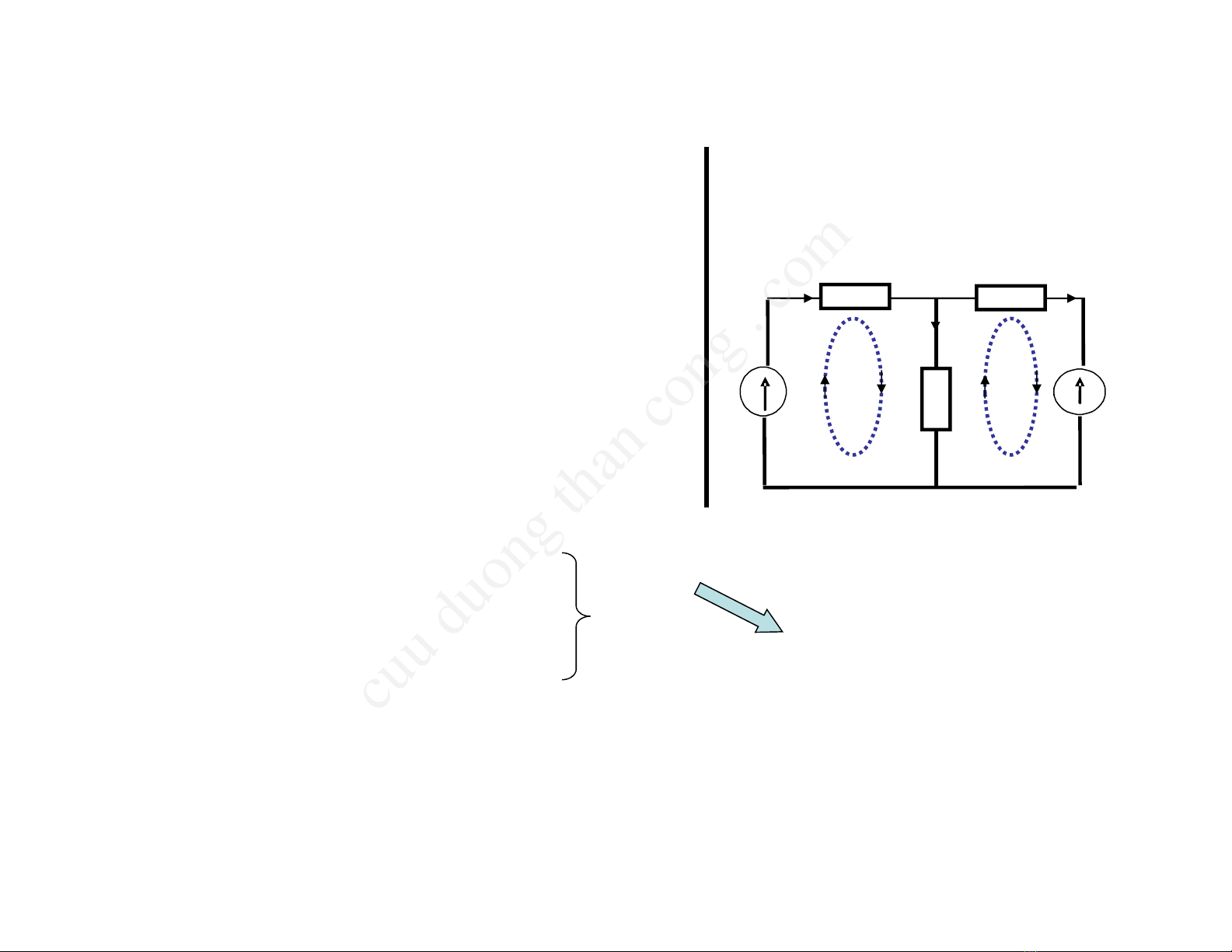
3.2 Phương pháp dòng điện vòng VD : - Chọn dòng trong các vòng độc lập làm ẩn om I11 Z 1 Z3 I3 3 - Viết hệ PT theo đ/l K2 .c 2I2 ng - Giải tìm nghiệm dưới dạng i vòng E1 Iv1 Z 2 Iv2 E3 co - i mỗi nhánh = tổng đại số các i vòng an khép qua nhánh đó th ng i i i (Z1 + Z2 ) I v1−Z2 I v2 = E1 i Biết Zk , E k o du i i i i i −Z2 Iv1 + (Z2 + Z3 ) Iv2 = − E3 Tìm được : I v1 , I v 2 u cu i i i i i => Dòng trong các nhánh : I1 = I v1 I 2 = I v1− I v2 i i I3 = I v2 CuuDuongThanCong.com https://fb.com/tailieudientucntt
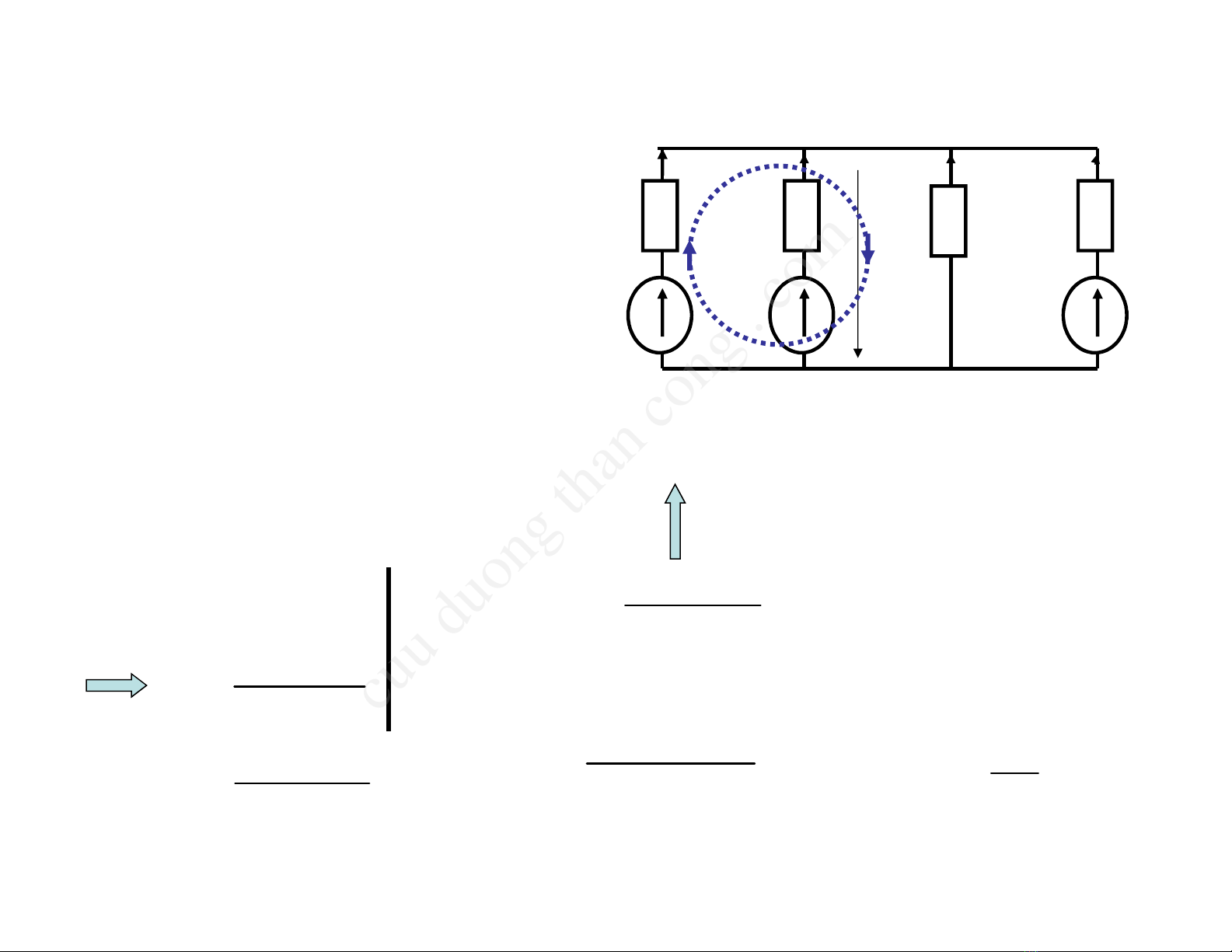
3.3 Phương pháp điện áp 2 nút A I1 I3 I4 - Chọn đ/a giữa 2 nút làm ẩn. I2 Z1 Z2 Z3 Z4 - Dựa vào đ/l K1,2 lập các om PT để tìm đ/a giữa 2 nút. UAB .c E1 E2 E4 - Tìm lại dòng trong các nhánh ng dựa vào U giữa 2 nút B co k = n (4) i ∑ an - Tại A, theo K1 có : Ik = 0 (1) th ng k =1 i i i i i Z1 I1 + U AB = E1 TQ Ik = E k − U AB i o (2) du i i Zk E1− U AB u i I1 = cu i i Z1 i k = n (4) i E k − U AB 1 TT: I2 = E 2 − U AB i ∑ Zk =0 Đặt Zk = Yk Z2 k =1 CuuDuongThanCong.com https://fb.com/tailieudientucntt
k = n (4) i i ∑k =1 Yk (E k − U AB ) = 0 i E k − U AB i i Ik = (2) Zk om k = n (4) k = n (4) .c i i ∑ (Yk E k ) = ∑ (Yk U AB ) ng k =1 k =1 co an i k = n (4) k = n (4) i U AB ∑ Yk = ∑ (Yk E k ) th ng k =1 k =1 o du k= n (4) i ∑ (E k Y ) u k cu i k=1 (3) U A B = k= n (4) ∑ k=1 Y k CuuDuongThanCong.com https://fb.com/tailieudientucntt
BT về nhà : Giải bài toán 3 nhánh biết : Z1 = 3 + j 4 = Z2 = Z3 om i i j90 E1 = 200e E3 = 200e j0 .c ng i co Tìm dòng I K và công suất P,Q,S toàn mạch theo 3 phương an pháp dòng nhánh, dòng vòng và điện áp 2 nút th o ng du u cu CuuDuongThanCong.com https://fb.com/tailieudientucntt
3.4 Phương pháp biến đổi tổng trở tương đương: 1. Tổng trở nối tiếp : Z1 Z2 Zn Znt om .c k =n k =n k =n Với : Znt = ∑Z = R nt + jX nt ng k = ∑ R k + j∑ X k co k =1 k =1 k =1 an th 2. Tổng trở song song : ng Với : Z1 Z2 Zn Z// o du u 1 Z// = = R // + jX // cu k =n 1 ∑ Z1Z2 k =1 Z k Z // = Z1 + Z2 Khi có 2 Tổng trở // CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ : Z1 = 3 + j 4 ; Z2 = 8 – j 6 Z1 Z2 - Cho Z1 nối tiếp Z2 om => Znt = 11 – j 2 = .c Znt ng -2 jartg 112 + 2 2 e = 11,18e − j10 18' co Znt = 11 an Z1 Z2 th - Cho Z1 // Z2 : ng Z1Z2 Z // = o Z1 + Z2 du Z// u cu (3 + j4)(8 − j6) 5e j53 8'10e − j36 52' Z // = = = 4, 47e j26 34' 11,18e − j10 18' 11,18e − j10 18' CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ 2 : Cho MĐ như hình bên: I biết U~ = 100 V; XL = XC = 10 Ω IL IC U XL XC om Tìm IL, IC , I ? .c * Dùng VT IC ng co an U th ng * Dùng TĐ IL o du Z = R + j(XL – XC) Z1Z2 u Z // = ZL = j XL cu Z1 + Z2 j10*(− j10) ZC = - j XC I = IL + IC = 0 Z// = =∞ j10 − j10 I=0 Cộng hưởng dòng điện CuuDuongThanCong.com https://fb.com/tailieudientucntt
∆) 3. Chuyển đổi sao (Y)– tam giác (∆ 1 1 om Z1 Z12 Z31 .c Z3 ng Z2 2 2 3 co 3 Z23 an th 1. Biết Z1, Z2, Z3 nối sao : ng Khi có Z1= Z2= Z3 = ZY Z1Z2 Sao đối xứng Z12 = Z1 + Z2 + o du Z3 Z 2 Z3 u Z23 = Z2 + Z3 + cu Z1 Z12= Z23= Z31 = Z∆ = 3 ZY Z3 Z1 Z31 = Z3 + Z1 + Z2 CuuDuongThanCong.com https://fb.com/tailieudientucntt
2. Biết Z12, Z23, Z31 nối tam giác : 1 1 om Z1 Z12 Z31 .c Z3 ng Z2 2 2 3 co 3 Z23 an Z12 Z13 Z1 = Z12 + Z23 + Z31 th ng Khi có Z12= Z23= Z31 = Z ∆ o Z23 Z21 Z2 = du Z12 + Z23 + Z31 Tam giác đối xứng u cu Z31Z32 Z3 = Z∆ Z12 + Z23 + Z31 Z1= Z2= Z3 = ZY= 3 CuuDuongThanCong.com https://fb.com/tailieudientucntt
3.5 Phương pháp xếp chồng *) Trong MĐ có nhiều nguồn kích thích, đáp ứng dòng, áp trên mỗi nhánh bằng tổng đại số của các dòng áp ứng với từng nguồn kích om thích riêng rẽ .c I33 I1 I11 ng I2 I3 I21 I31 co Z1 Z3 Z3 Z2 = Z1 Z2 + Z1 Z2 Z3 an E1 E3 E1 I13 I23 E3 th o ng i i i i i i i i i I3 = − I31 + I33 du I1 = I11− I13 I 2 = − I 21 − I 23 u cu Phương pháp xếp chồng chỉ ứng dụng với mạch tuyến tính CuuDuongThanCong.com https://fb.com/tailieudientucntt
*) Mạch điện có nguồn chu kỳ không sin e (t) u (t) 2 1 .5 om 1 0 .5 t 0 .c -0 .5 -1 ng -1 .5 -2 0 2 4 6 8 10 12 14 co VD : u(t) = U o + 2U1 sin(ωt + ψ1 ) + 2U 3 sin(3ωt + ψ 3 ) an th Cách giải: - Coi bài toán được cấp bởi nhiều nguồn ng - Lần lượt cho từng nguồn thành phần tác dụng . . o du - Áp dụng các phương pháp đã học để giải Ik , U k . . u - Đổi I k , U k về dạng tức thời cu - Xếp chồng các k =n . k =n thành phần dạng tức thời: i (t ) = i k ( t ) u (t ) = u k ( t ) k =0 ∑ ∑ k =0 CuuDuongThanCong.com https://fb.com/tailieudientucntt
*) Trị hiệu dụng của dòng chu kỳ không sin Công thức tổng quát: om T 1 I= ∫ dt i 2 .c T 0 ng Suy ra: co an T T 1 1 I= ∫∑ i = ∑ ∫ ik dt 2 2 th k dt T T ng 0 0 Ik2 o Vì vậy ta có trị hiệu dụng của hàm không sin: du u n cu n n ∑ Ik U= ∑U E= ∑E 2 2 I= 2 k k 0 0 0 CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ: Cho mạch điện như hình bên. Io Zo A Biết: I2 I1 Zo = 5 + j 5 Ω; Z1 = 3 + j 4 Ω; X1 X2 om UAB Z2 = 8 – j 6 Ω; UAB = 100 V U .c R1 R2 ng Tìm : I1, I2 , Io , U co B P, Q, S, cosϕ toàn mạch an th Giải TT: o ng 1. Tìm : I1, I2 , Io , U du U AB I2 = u U AB 100 Z2 cu I1 = = = 20 (A) Z1 32 + 42 = 100 = 10 (A) 82 + 6 2 CuuDuongThanCong.com https://fb.com/tailieudientucntt
Để tìm Io Io Zo A - Véc tơ I2 I1 có thể dùng - số phức X1 X2 om UAB - qua P,Q,S U .c R1 R2 ng C1. Dùng véc tơ co B an I1 chậm sau U AB 1 góc I2 th 4 ng 36o52’ I1 I2 ϕ1 = arctg = 53o8’ 3 U AB o du 53o8’ u I 2 vượt trước U AB 1 góc cu I0 6 I1 ϕ 2 = arctg = 36o52’ 8 Io = 202 +102 = 22,36 (A) CuuDuongThanCong.com https://fb.com/tailieudientucntt
C2. Dùng số phức i Io Zo A j0 j0 i U AB 100e 100e I1 = = = j53 8' I2 Z1 3 + j4 5e I1 X2 X1 om i UAB I1 = 20e− j53 8' U .c R1 R2 ng i i U AB 100e j0 100e j0 = = co I2 = B Z2 8 − j6 10e− j36 52' an th i I 2 = 10e j36 52' o ng i i i Io = I1 + I 2 = 20e − j53 8' +10e j36 52' = 12 − j16 +8 + j6 = 20 – j 10 du u cu i Io = 22,36e− j26 34' CuuDuongThanCong.com https://fb.com/tailieudientucntt
Io Zo A C3. Dùng qua P,Q, S I2 I1 X1 X2 om 2 PAB = R1I1 + R2I2 2 UAB U .c R1 R2 ng PAB = 3.202 + 8.102 = 2000 W co B an QAB = X1I12 - X2I22 = 4.202 - 6.102 = 1000 VAr th Cụm AB ng SAB = PAB + Q AB 2 2 = 20002 + 10002 o = 2236 VA du u cu SAB 2236 SAB = U AB Io Io = = = 22,36 A U AB 100 CuuDuongThanCong.com https://fb.com/tailieudientucntt
2. Tìm P, Q, S, cosϕ toàn mạch Io Zo A I2 2 P = RoIo + PAB I1 X1 X2 om UAB P = 5.22,362 + 2000 = 4500 W U .c R1 R2 ng Q = XoIo2 + QAB co B Q= 5.22,362 + 1000 = 3500 VAr an th = 45002 + 35002 Cụm AB S = P +Q = 5700 VA 2 2 o ng du S 5700 S = U Io U= = = 255 V u cu Io 22,36 P 4500 cosϕ = = = 0,79 S 5700 CuuDuongThanCong.com https://fb.com/tailieudientucntt