
B MÔN TOÁN NG D NG - ĐHBKỘ Ứ Ụ
-------------------------------------------------------------------------------------
PHƯƠNG PHÁP TÍNH
CHƯƠNG 4
TÍNH G N ĐÚNG Đ O HÀM & TÍCH PHÂNẦ Ạ
•TS. NGUY N QU C LÂN (11/2006)Ễ Ố

N I DUNGỘ
---------------------------------------------------------------------------------------------------------------------------------
A- TÍNH G N ĐÚNG Đ O HÀMẦ Ạ
1- Đ O HÀM C P 1: SAI PHÂN 2 ĐI M TI N – LÙI, 3 Ạ Ấ Ể Ế
ĐI M TI N – LÙI - HỂ Ế Ư NG TÂM Ớ
B- TÍNH G N ĐÚNG TÍCH PHÂNẦ
2 - TÍNH Đ O HÀM B C CAOẠ Ậ
1- H S NEWTON-COTESỆ Ố
2- CÔNG TH C HÌNH THANG & SIMPSONỨ
3- GI M SAI SẢ Ố

MINH HO Ý TẠ Ư NGỞ
--------------------------------------------------------------------------------------------------------------------------------
Tính x p x : a/ Đ o hàm f’ t i m c xấ ỉ ạ ạ ố 1: f’(0.4)
( )
∫
6.0
3.0
/dxxfb
Hàm y = f(x), ho c xác ặđ nh qua b ng giá tr , ho c bi u ị ả ị ặ ể
th c ph c t p (không d tìm f’ hay ứ ứ ạ ễ ∫) → Thay b ng b ngằ ả
Moác xk 0.3 0.4 0.6
Giaù Trò yk =
f(xk)
0.355 0.36 0.4
Xây d ng ựđa th c n i suy L(x) t b ng ứ ộ ừ ả {( xk, f(xk) )}, k = 0 … 2
( )
( ) ( )
==
++=
36.04.0,355.03.0
2
LL
cbxaxxL
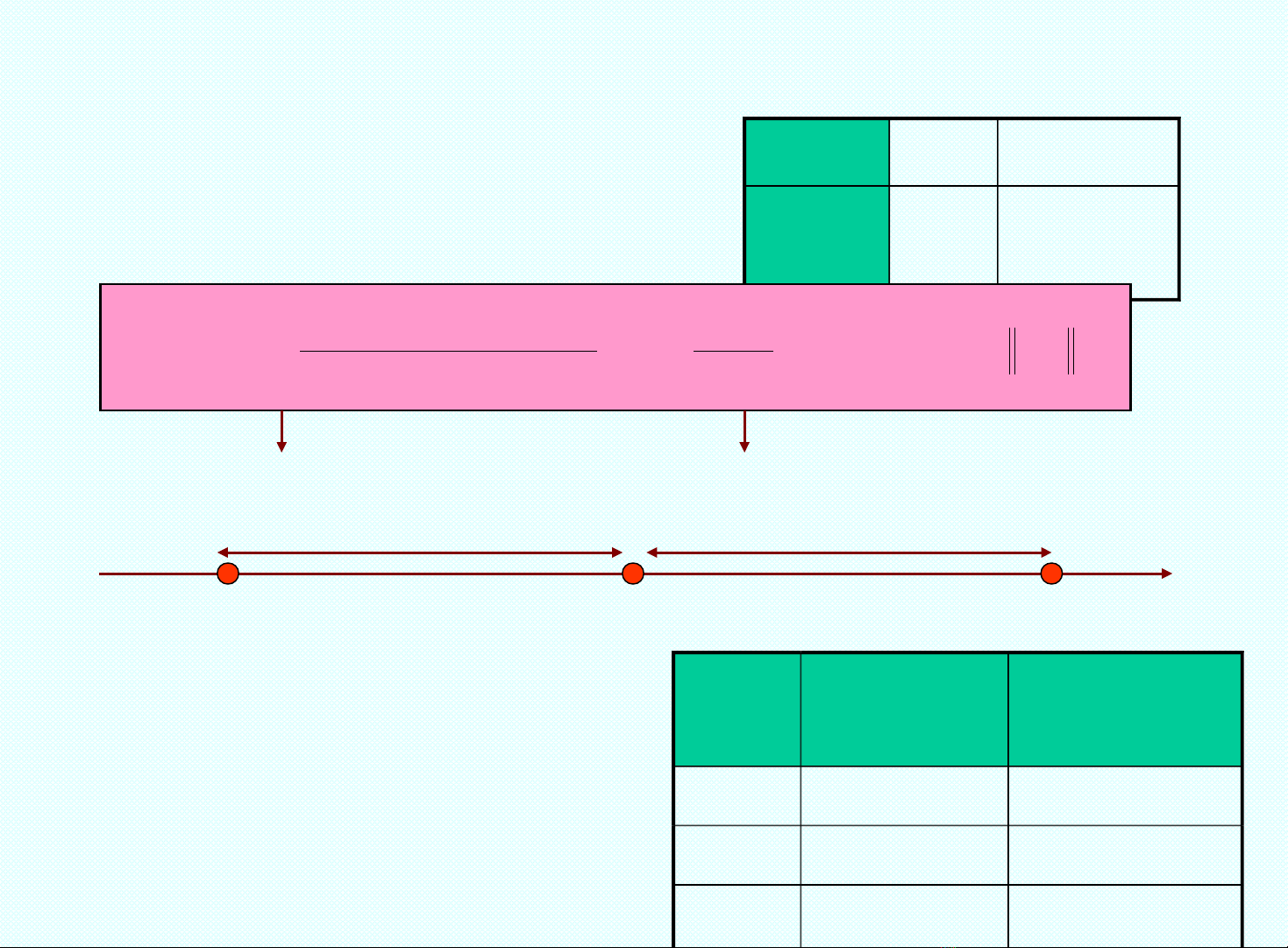
MINH HO CÔNG TH C Đ O HÀM 2 ĐI MẠ Ứ Ạ Ể
-------------------------------------------------------------------------------------------------------------------------------
2 đi m ể(x0, f(x0)) , (x0+h, f(x0+h)) Moác x0 x0 + h
Giaù
trò
f(x0) f(x0 +
h)
[ ]
''max,
2
,
)()(
)('
00
,
2
2
00
0
fM
hM
h
xfhxf
xf
hxx
+
==∆
−+
≈
Công th c x p xứ ấ ỉ Sai số
x0 – h x0x0 + h
h h
VD: X p x ấ ỉ f’(1.8) v i f(x) = ớ
lnx & h = 0.1 , 0.01 , 0.001
h Xaáp xæ C/xaùc
f’(x0)
0.1 0.5555556
0.01
0.00
1
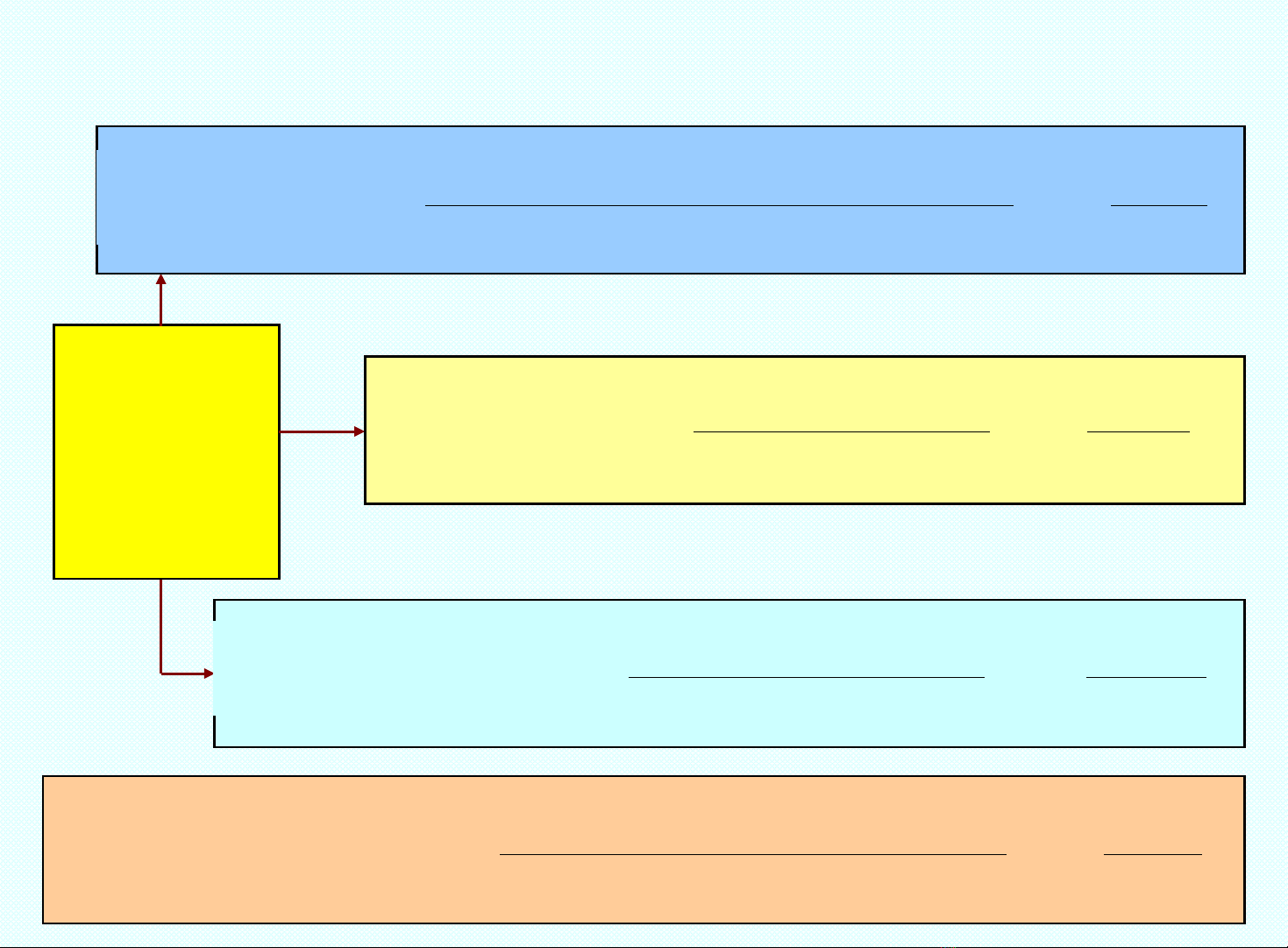
T NG K T X P X Đ O HÀMỔ Ế Ấ Ỉ Ạ
-------------------------------------------------------------------------------------------------------------------------------
X p x ấ ỉ
đ o hàm ạ
c p 1ấ
X p x f’’(xấ ỉ 0):
( ) ( ) ( ) ( )
12
,
2
''
2
4
2
000
0
hM
h
hxfxfhxf
xf
=∆
−+−+
≈
3 đi m:ể
3
,
2
)2()(4)(3
)('
2
3000
0
hM
h
hxfhxfxf
xf
=∆
+−++−
≈
2 đi m:ể
2
,
)()(
)('
2
00
0
hM
h
xfhxf
xf
⋅
=∆
−+
≈
Hưng tâm:ớ
6
,
2
)()(
)('
2
300
0
hM
h
hxfhxf
xf
⋅
=∆
−−+
≈


























