Môn họcMôn học
TÍN HIỆU VÀ HỆ THỐNGTÍN HIỆU VÀ HỆ THỐNG
Giảng viên: PGS. TS. Huỳnh Thái Hoàng
Khoa Điện – Điện Tử
Đại học Bách Khoa TPHCM
Email: hthoang@hcmut edu vn
Email:
hthoang@hcmut
.
edu
.
vn
Homepage: www4.hcmut.edu.vn/~hthoang/
1
Chương 4Chương 4
PHÂN TÍCH TÍN HIỆU LIÊN TỤC PHÂN TÍCH TÍN HIỆU LIÊN TỤC
DÙNG BIẾN ĐỔI DÙNG BIẾN ĐỔI FOURIERFOURIER
2
Biểdiễtí hiệkhô t ầhà bằtí h hâ F i
Nội dung chương 4Nội dung chương 4
Biể
u
diễ
n
tí
n
hiệ
u
khô
ng
t
u
ầ
n
h
o
à
n
bằ
ng
tí
c
h
p
hâ
n
F
our
i
e
r
Biến đổi Fourier của một số hàm thông dụng
Các tính chấtcủabiếnđổi Fourier
Các
tính
chất
của
biến
đổi
Fourier
Năng lượng tín hiệu
Tr
uyề
n
t
ín hi
ệu
qua
h
ệ
t
h
ố
n
g
LTI
C
uyềtệu qua ệtốgC
Các bộ lọc lý tưởng và thực tế
Ứng dụng trong viễn thông: điều chế AM
3
BIỄU DIỄN TÍN HIỆU KHÔNG TUẦN HOÀN BIỄU DIỄN TÍN HIỆU KHÔNG TUẦN HOÀN
BẰNG TÍCH PHÂN FOURIERBẰNG TÍCH PHÂN FOURIER
4
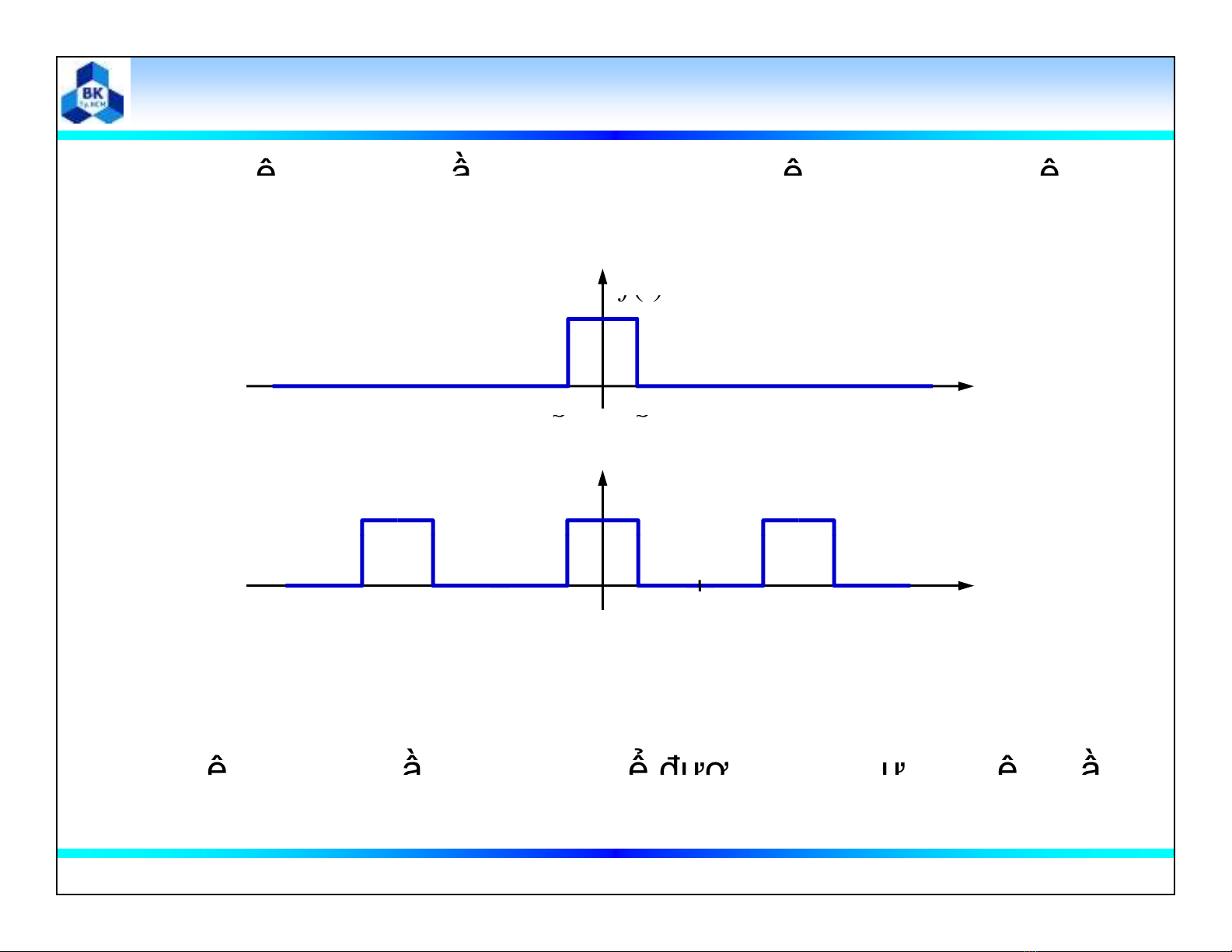
Tín hiệu không tuần hoànTín hiệu không tuần hoàn
Xét tín hiệu không tuần hoàn f(t) và tín hiệuf
(t) là tín hiệu
Xét
tín
hiệu
không
tuần
hoàn
f(t)
và
tín
hiệu
f
T0
(t)
là
tín
hiệu
tuần hoàn do sự lặp lại tín hiệu f(t) với chu kỳ T0:
f
t
)
f
)
t
S
S
S
S
)(
0tfT
t
S
ST0
Tín hiệu không tuần hoàn có thểđược xem nhưtín hiệutuần
Ta có quan hệ:)(lim)( 0
0
tftf T
T
5
Tín
hiệu
không
tuần
hoàn
có
thể
được
xem
như
tín
hiệu
tuần
hoàn có chu kỳ vô hạn.