Trường Đại học Công nghiệp thành phố Hồ Chí Minh
Khoa Công nghệ Cơ khí
CHƯƠNG 02:
TỐI ƯU HÀM MỘT BIẾN SỐ
Thời lượng: 3 tiết
2
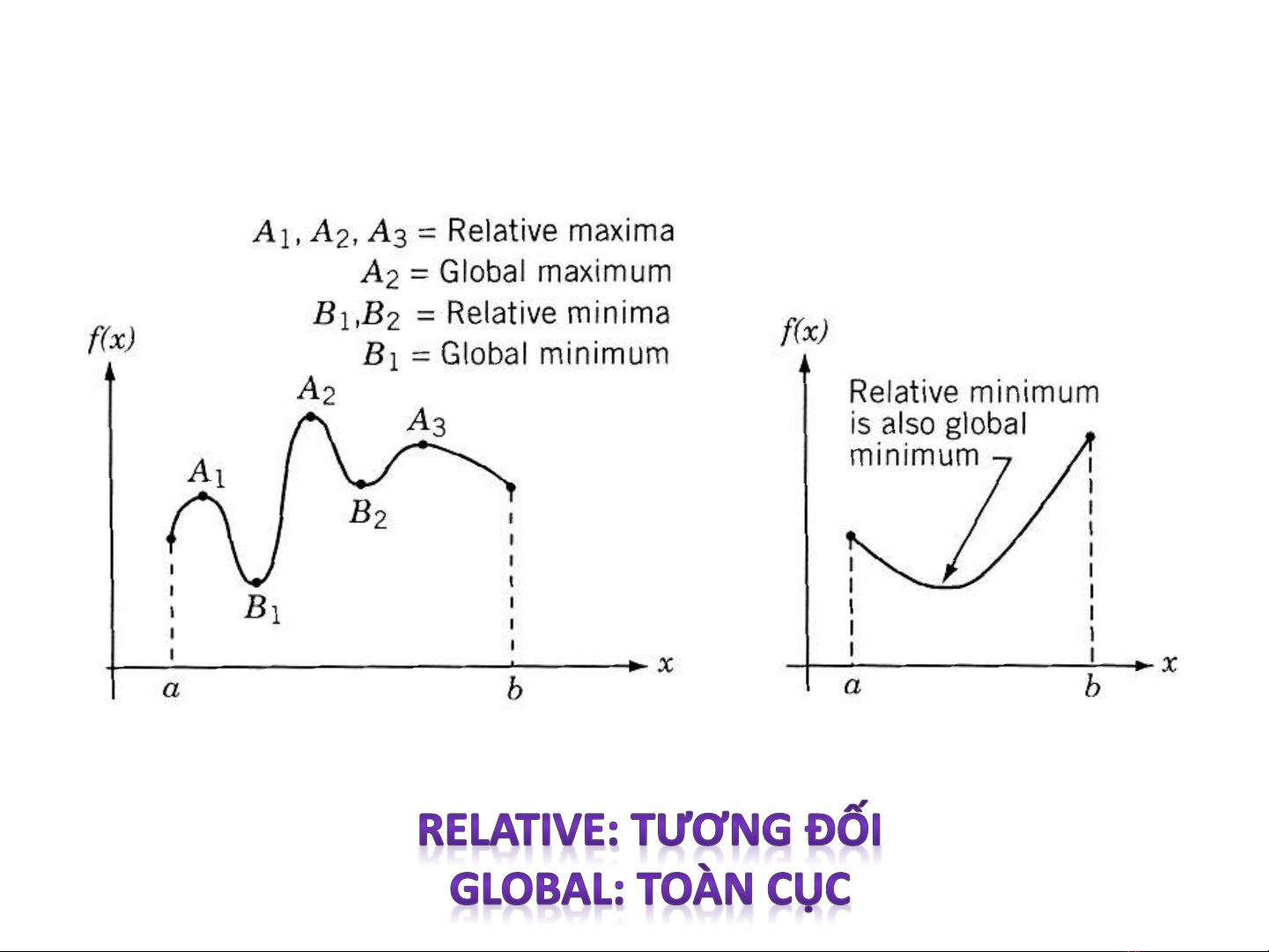
Cực trị địa phương (tương đối) và toàn cục
3
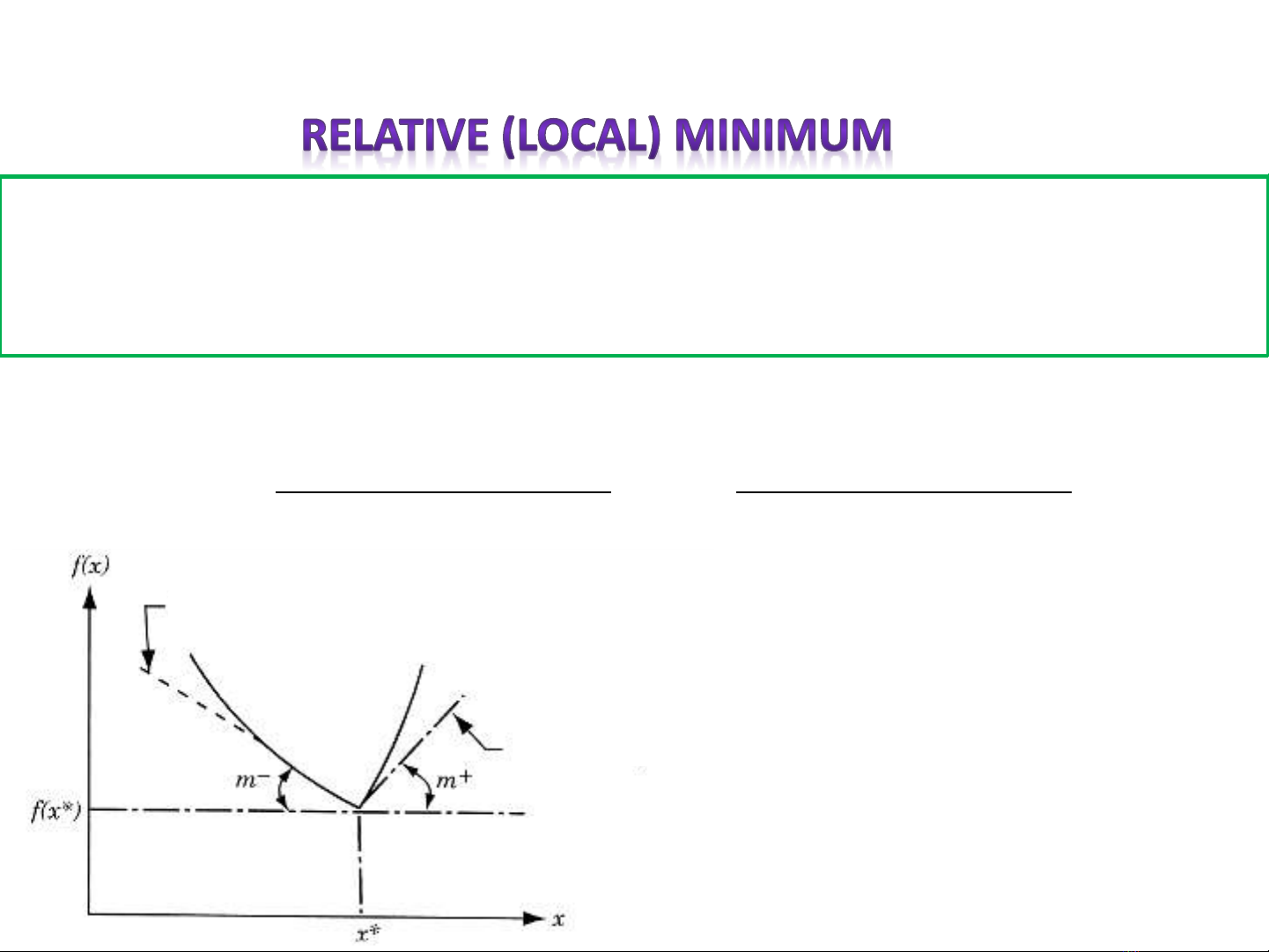
Điều kiện cần của cực trị địa phương
Nếu hàm số f(x) được xác định trên đoạn [a,b] và có cực trị địa
phương tại x=x* (a<x*<b) và nếu đạo hàm f’(x) tồn tại dưới dạng
một số hữu hạn tại x=x* thì f’(x*) = 0
Đạo hàm f’(x*) không tồn tại khi mà:
00
lim lim
hh
f x h f x f x h f x
mm
hh



Độ dốc m-
Độ dốc m+
Tại điểm đầu (x=a) và cuối
đoạn (x=b) giới hạn trên
chỉ tồn tại với h<0 hoặc
h>0, nên đạo hàm là
không xác định tại các
điểm đầu và cuối đoạn.
4
Điều kiện đủ của cực trị địa phương
10
nn
f x f x f x f x
n là số chẵn n là số lẻ
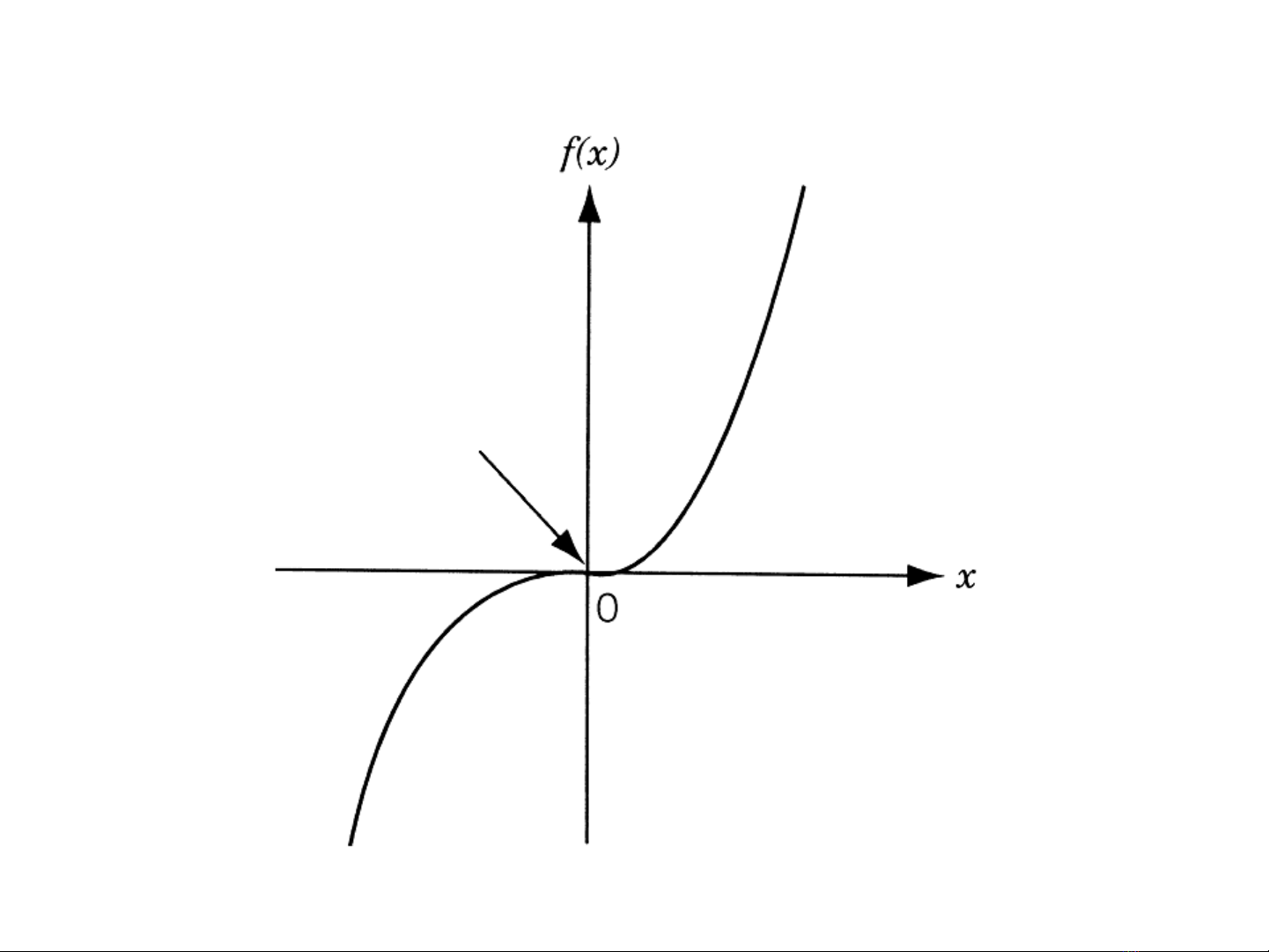
Điểm uốn
(Inflection Point)
0
n
fx
0
n
fx
Cực tiểu Cực đại
Điểm dừng
5
Điểm dừng (Stationary point)
Điểm dừng, f’(x)=0