
SƠ LƯỢC VỀ CHUỖI
FOURIER
Ta đã biết về việc một hàm số, dưới điều kiện nào đó, có thể được
khai triển thành một chuỗi lũy thừa, tức là chuỗi Taylor. Trong
chương này, chúng ta tìm hiểu một kiểu khai triển khác, khai triển
thành chuỗi các hàm sin và cos.

Số thực Chuỗi số Hàm số liên tục Đạo hàm Tích phân Chuỗi Fourier
Chuỗi Fourier
◮Định nghĩa chuỗi Fourier
◮Sự hội tụ của chuỗi Fourier
◮Khai triển chuỗi Fourier của hàm số xác định trên [0, π]
◮Khai triển chuỗi Fourier của hàm số xác định đoạn [a,b]
VI TÍCH PHÂN 1B 299/320
Số thực Chuỗi số Hàm số liên tục Đạo hàm Tích phân Chuỗi Fourier
Định nghĩa chuỗi Fourier
Định nghĩa chuỗi Fourier
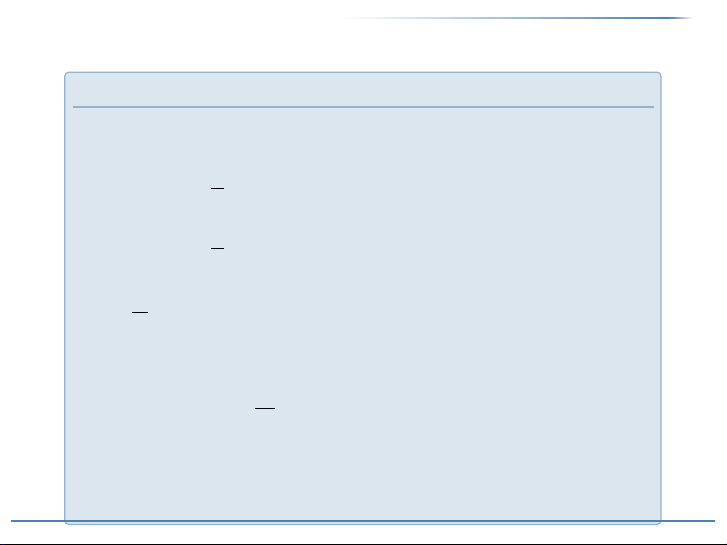
Xét flà hàm số khả tích trên đoạn [−π, π]. Đặt
ak=1
πZπ
−π
f(x)cos kx dx,k=0,1,2,3. . . (22)
bk=1
πZπ
−π
f(x)sin kx dx,k=1,2,3. . . (23)
Chuỗi a0
2+P∞
k=1(akcos kx +bksin kx )được gọi là chuỗi Fourier
(cũng được gọi là chuỗi lượng giác) của hàm số f, và ta viết
f(x)∼a0
2+
∞
X
k=1
(akcos kx +bksin kx )(24)
Các hệ số ak,bkđược tính theo công thức (22)–(23) được gọi
là các hệ số Fourier của hàm số f.
VI TÍCH PHÂN 1B 300/320

Số thực Chuỗi số Hàm số liên tục Đạo hàm Tích phân Chuỗi Fourier
Sự hội tụ của chuỗi Fourier
Cũng như chuỗi Taylor, quan hệ (24) không nói lên điều gì về sự
hội tụ của chuỗi Fourier. Hơn nữa, cho dù chuỗi Fourier của fcó
hội tụ thì tổng của chuỗi này cũng chưa hẳn đã bằng f(x).
Ta có kết quả sau
VI TÍCH PHÂN 1B 301/320
Số thực Chuỗi số Hàm số liên tục Đạo hàm Tích phân Chuỗi Fourier
Sự hội tụ của chuỗi Fourier
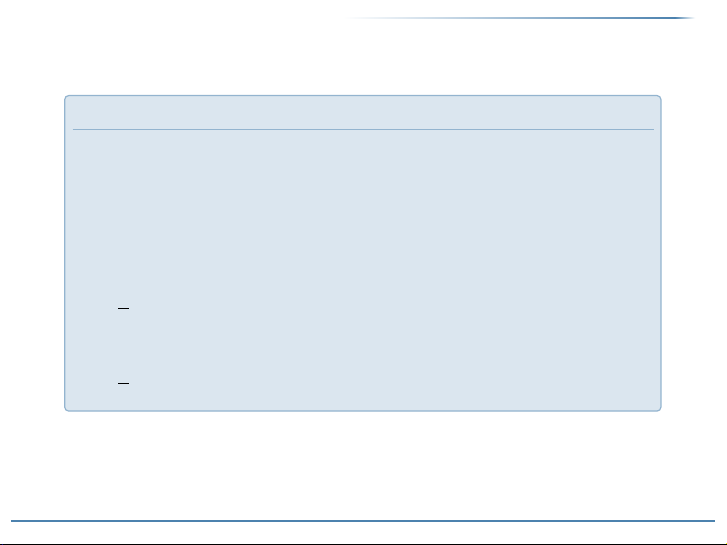
Định lý 1 (Dirichlet)
Nếu hàm số fđơn điệu từng khúc trên đoạn [−π, π], bị chặn
trên đoạn đó, nghĩa là ∀x∈[−π, π],|f(x)| ≤ M(Mlà hằng
số độc lập với x), thì chuỗi Fourier của fhội tụ tại từng điểm
x∈[−π, π]và tổng của chuỗi này bằng
(i) f(x)nếu fliên tục tại x,−π < x< π.
(ii) 1
2[f(x−) + f(x+)] nếu xlà điểm gián đoạn kiểu bước nhảy
của f,−π < x< π.
(iii) 1
2[f(−π+) + f(π−)], nếu x=±π.
Nhắc lại. xlà điểm gián đoạn kiểu bước nhảy nghĩa là tồn tại
f(x−)và f(x+)nhưng f(x−)6=f(x+).
VI TÍCH PHÂN 1B 302/320


























