BÀI TẬP HÀM NHIỀU BIẾN
Tìm miền xác định của hàm
1) u = 222 yxa −− . 2) u = arcsin 2
y
x. 3) u = ln(2z2 – 6x2 – 3y2 – 6)
Gi
ớ
i h
ạ
n của hàm nhiều biến
1) Chứng minh rằng đối với hàm f(x, y) = yx
yx
+
−
;
;
1),(limlim 00 =
⎟
⎠
⎞
⎜
⎝
⎛
→→ yxf
yx
(
)
1),(limlim 00
−
=
→→ yxf
xy . Trong khi đó không tồn tại. ),(lim
0
0yxf
y
x→
→
2) Chứng minh rằng đối với hàm f(x, y) = 222
22
)( yxyx
yx
−+ . Có =
⎟
⎠
⎞
⎜
⎝
⎛
→→ ),(limlim 00 yxf
yx
(
)
),(limlim 00 yxf
xy →→ = 0. Nhưng không tồn tại . ),(lim
0
0yxf
y
x→
→
3) Tìm các giới hạn kép sau đây:
a.) 22
lim yxyx
yx
y
x+−
+
∞→∞→ . b) x
xy
ay
x
sin
lim
0
→
→. c)
(
)
)(22
lim yx
y
xeyx +−
+∞→+∞→ +.
d)
(
)
22
22
0
0
lim yx
y
xyx +
→
→. e) yx
x
ay
xx
+
→∞→ ⎟
⎠
⎞
⎜
⎝
⎛+
2
1
1lim . f) 22
0
1
)ln(
lim yx
ex y
y
x+
+
→
→.
Xét s
ự
liên t
ụ
c của hàm nhiều biến
1) Chứng minh rằng hàm số:
⎪
⎩
⎪
⎨
⎧
+
=
0
2
),( 22 yx
xy
yxf nếu x2 + y2 ≠ 0
nếu x2 + y2 = 0
Liên tục theo mỗi biến x và y riêng biệt (với
giá trị cố định của biến kia), nhưng không liên tục
đồng thời theo cả hai biến đó.
2) Chứng minh rằng hàm số:
⎪
⎩
⎪
⎨
⎧
+
0
22
2
yx
yx nếu x2 + y2 ≠ 0
nếu x2 + y2 = 0
Liên tục tại điểm (0, 0).
Đạo hàm riêng của hàm nhiều biến
1) Cho hàm số: f(x, y) = x + (y – 1)arcsin y
x tìm f’x(x, 1).
2) Cho u = x2 – 3xy – 4y2 – x + 2y + 1. Tìm
x
u
∂
∂
và y
u
∂
∂
.
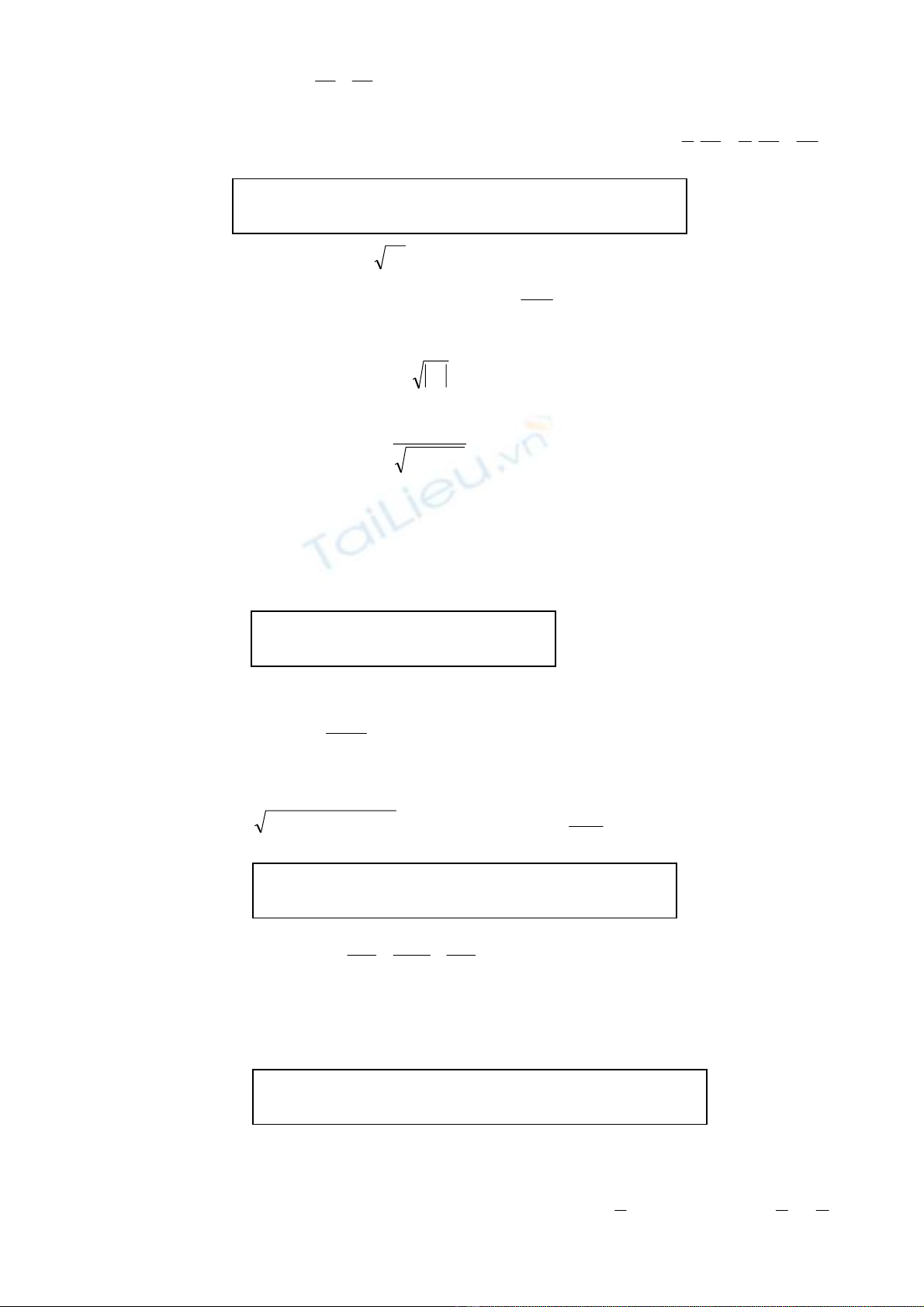
3) z = , tìm
22 yx
e+
x
z
∂
∂, y
z
∂
∂.
4) Chứng tỏ rằng, hàm z = yln(x2 – y2), thoả mãn phương trình:
x
1
x
z
∂
∂+y
1
y
z
∂
∂=2
y
z
Xét sự khả vi của hàm
1) Cho hàm u = f(x, y) = 3xy . Hàm số đó có khả vi tại điểm O(0, 0) hay không?
2) Khảo sát tính khả vi của hàm f(x, y) = 22
1
yx
e+
−
khi x2 + y2 > 0 và f(0, 0) = 0 tại điểm
O(0, 0).
3) Chứng minh rằng f(x, y) = xy liên tục tại O(0, 0), có cả hai đạo hàm riêng f’x(0,
0), f’y(0, 0) tại điểm đó, tuy nhiên hàm này không khả vi tại O(0, 0).
⎪
⎩
⎪
⎨
⎧
+
=
0
),( 22 yx
xy
yxf nếu x2 + y2 ≠ 0
nếu x2 + y2 = 0
4) Cho hàm
khi x ngoài đoạn [a, b]
Chứng minh rằng trong lân cận của điểm (0, 0), hàm liên tục và có các đạo hàm
riêng f’x(x, y), f’y(x, y) giới nội. Tuy nhiên hàm đó không khả vi tại điểm O(0, 0).
Tìm vi phân của hàm
1) Tìm du nếu:
a.) u = arctg yx
yx
−
+. b) u = .
zy
x2
2) Bằng cách thay số gia của hàm bởi vi phân, hãy tính gần đúng:
a.) 015,02 .855.1sin e+. b) arcrg 95,0
02,1 .
Đạo hàm riêng và vi phân cấp cao
1) Cho u = ylnx. Tìm 2
2
x
u
∂
∂, yx
u
∂∂
∂2
, 2
2
y
u
∂
∂.
2) Cho u = sinx.siny. Tìm d2u.
3) Cho u = x2y. Tìm d3u.
Tìm cực trị của hàm nhiều biến
1) Tìm cực trị của hàm
a.) u = x2 + xy + y2 – 3x – 6y. b) u = 2
1xy + (47 – x – y)( 3
x + 4
y).

c) u = x + x
y
4
2
+y
1+2. d) u = 1 - 22 yx +.
2) Tìm cực trị có điều kiện của hàm: u = xy với điều kiện x2 + y2 = 2a2.
3) Tìm cực trị của hàm f(x, y, z) = x +
x
y+y
z+z
1.
4) Tìm cực trị của hàm f(x, y) = x + y với điều kiện: 4
2
x+9
2
y= 1.
5) Tìm cực trị của hàm f(x, y, z, u) = x + y + z + u với điều kiện:
g(x, y, z, u) = 16 – xyzu = 0.


























