BÀI TẬP LỚN VÀ SỨC BỀN VẬT LIỆU

Chia sẻ: Bui Thanh Thien | Ngày: | Loại File: PDF | Số trang:22

Thêm vào BST

Báo xấu

176
lượt xem 31
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Sau khi xác định được 2 phản lực liên kết tại B, ta đi vẽ biểu đồ M, N, Q cho hệ tĩnh định tương đương ( hệ siêu tĩnh ). X1 và Y1 đều dương vậy chiều đúng với giả thiết. Để vẽ được các biểu đồ nội lực thì ta đặt các lực X1 và Y1 vào hệ cơ bản, xác định các giá trị nội lực tại A và C.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: BÀI TẬP LỚN VÀ SỨC BỀN VẬT LIỆU

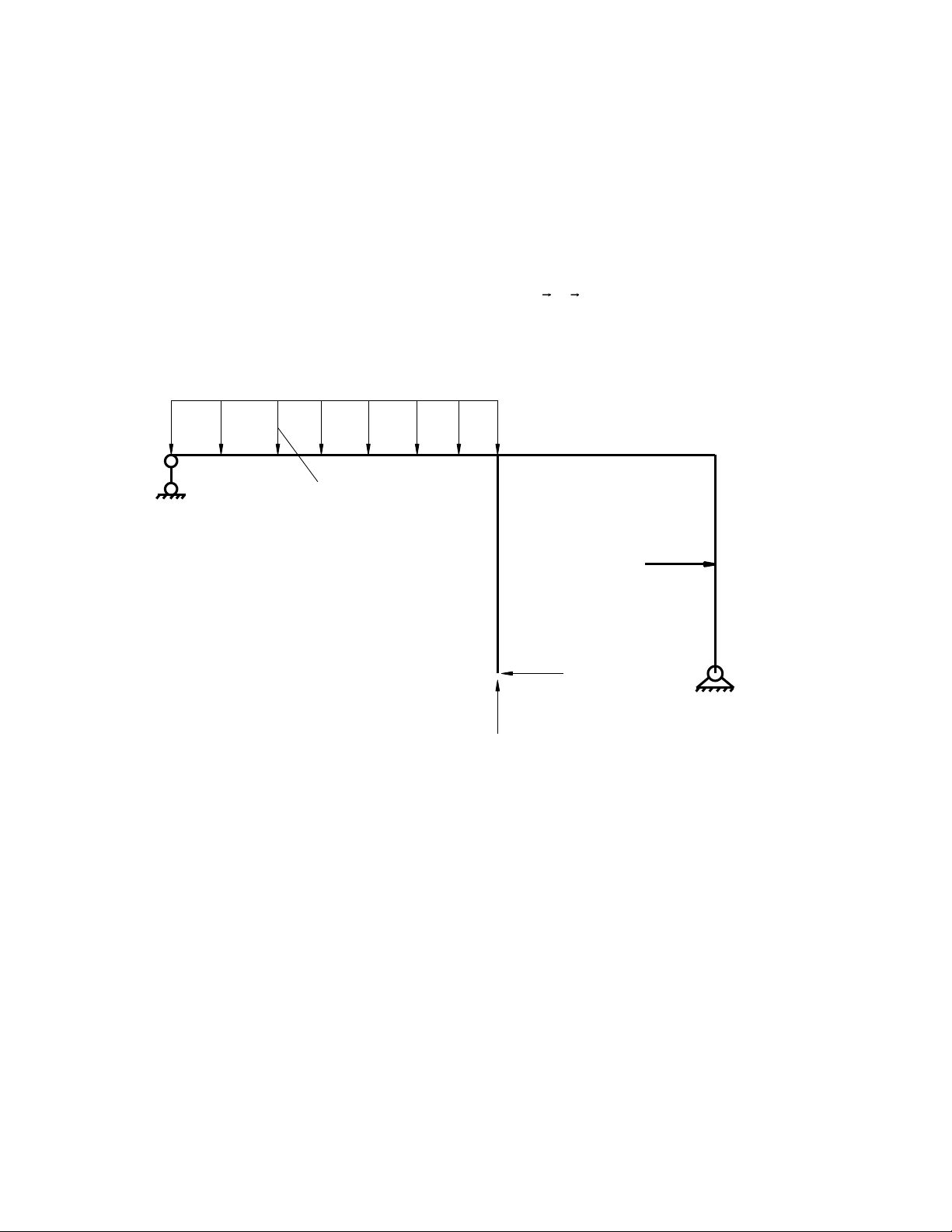
BÀI TẬP LỚN SỨC BỀN VẬT LIỆU BÀI TẬP A (Sơ đồ 8 - Số liệu 4) 3L 2L q L P=3qL 2L L Chọn hệ cơ bản: Bỏ hai liên kết tại B ta được hệ cơ bản như hình vẽ: C B A 1
Ta có hệ tĩnh định tương đương: Liên kết tại B có 2 thành phần phản lực theo 2 phương vuông góc. Do đó khi bỏ liên kết đó đi ta phải đặt vào các phản lực ( X 1 ; Y1 ) theo 2 phương để thay thế ( hình vẽ ) C q P=3qL B X1 A Y1 Vẽ Biểu Đồ Momen M1, M2,Mp : M1: Biểu đồ momen đơn vị do X1 = 1 gây nên. Đặt lực X1 = 1 vào hệ cơ bản như hình vẽ. Xác định các phản lực liên kết tại gối A và C 2
C YC B X1 XA A YA   x( P )  0  X i 1  X A  0  X A   X 1  1  m( B)  0  YC .3L  YA .2 L  0     YC  YA  0   y ( Pi )  0  YC  YA  0 Sau khi xác định được các phản lực liên kết ta vẽ được biểu đồ M1: 2L 2L C 2L X1=1 B A 3
M2: Biểu đồ momen đơn vị do Y1 = 1 gây nên. Đặt lực Y1 = 1 vào hệ cơ bản như hình vẽ. Xác định các phản lực liên kết tại gối A và C C YC B XA A Y1 YA  Ta có XA=0  2qL  m( A)  0  YC .5L  Y1.2 L  0 YC    5     y ( Pi )  0  YA  YC  Y1  0  YA  YC  1 Y  3qL   A  5 Sau khi xác định được các phản lực liên kết tại các gối, ta vẽ được biểu đồ M2: 1,2L C B A Y1=1 4
Mp: Biểu đồ momen do tải trọng đặt nên hệ cơ bản gây nên. Xác định các phản lực liên kết tại gối A và C. C q Yc P=3qL B XA A YA   x( P )  0  X i A  P  0  X A  3qL  y ( Pi )  0  YA  YC  3qL     YC  YA  1,5qL   m( A)  0  5L.YC  3qL.1  3qL.3,5L  0 Sau khi xác định được các phản lực liên kết ta vẽ được đồ thị Mp: 3qL2 C 1,12qL2 B A 5
3qL2 C 1,12qL2 B A 1,2L (Mp) C B A (M2) 2L 2L C 2L B A (M1) 6
Xác định phương trình chính tắc: 1 1 2  40 L 3 11  ( M1 )  ( M1 )    2 L  2 L   2 L   EJ  2 3  3EJ 1 1 2 1 2  12 L 3  22  (M 2 )  ( M 2 )   1, 2 L  3L  1, 2 L  1, 2 L  2 L  1, 2 L   EJ  2 3 2 3  5EJ 1  1  12 L 3 12   21  ( M1 )  ( M 2 )   2 L  2 L  1, 2 L   EJ  2  5EJ 1  1 3 1  25qL4 1 p  (M p )  (M1 )    3qL  2 L  2 L  3qL  L   2 L  3qL  L   2 L   2 2 2 EJ  2 4 3  2 EJ 1  2 1 1 2 1  18qL 4 2 p  (M p )  (M 2 )   1,12qL  3L  1, 2 L  3qL  2 L  1, 2 L   2 EJ  3 2 2 3  125EJ Ta có phương trình chính tắc: 11  X 1  12  Y1  1 p  0    21  X 1   22  Y1   2 p  0    40 12 25qL  3 X1  Y1  0  5 2   12 X  12 Y  18  0  5  1 5 1 125 7
Giải phương trình ta được:  X 1  1,16qL  Y1  1, 22qL Sau khi xác định được 2 phản lực liên kết tại B, ta đi vẽ biểu đồ M, N, Q cho hệ tĩnh định tương đương ( hệ siêu tĩnh ). X1 và Y1 đều dương vậy chiều đúng với giả thiết. Để vẽ được các biểu đồ nội lực thì ta đặt các lực X1 và Y1 vào hệ cơ bản, xác định các giá trị nội lực tại A và C. C q YC P=3qL B X1 XA A Y1 YA  x(P )  0  X  X  P  0  X  P  X  3qL 1,16qL  1,84qL i A 1 A 1  y ( P )  0  Y  Y  Y  3qL  0  Y  Y  3qL  1, 22qL  1, 78qL i A C 1 A C    3L   m( A)  0  YC .5L  Y1.2 L  P.L  3qL  2 L  0   2  YC  1, 01qL  YA  0, 77qL Sau khi xác định được các phản lực liên kết tại gối A và C, ta vẽ được biểu đồ M, Q, N cho hệ TDTD như hình sau : 8
1,16qL Nz 1,22qL 0,77qL 1,99qL 0,77qL 1,01qL 1,84qL 1,16qL 1,16qL 1,46qL2 Qy 2,32qL2 0,68qL2 0,51qL2 0,86qL2 1,84qL2 Mx 9
CÂN BẰNG NÚT: 3L 2L C D E q L P=3qL 2L L B A 1. Xét nút E:  x  0  m  0 p  Nút cân bằng 1,16qL 0,68qL2 E 1,16qL 0,68qL2 10
2. Xét nút D: 0,77qL 0,68qL2 D 1,16qL 1,99qL 0,68qL2 0,68qL2 1,16qL 1,22qL  x  0  m  0 p => Nút cân bằng 11
BÀI TẬP B (Sơ đồ 8 – số liệu 4) Phần I: Sơ đồ hóa I. Thiết lập bản vẽ tính toán. - Đặt lực tại vị trí ăn khớp. - Chuyển lực về đường trục. Z2 Z'2 Z1 A D B C ' P2 Z1 A2 t T2 T1 2t P1 2a a a a a P2 A2 Mx Ma2 T1 3t T2 My P1 Md Mz M2 M1 12
- Phân lực về các mặt phẳng: o Mặt phẳng thẳng đứng yOz o Mặt phẳng nằm ngang xOz o Mặt phẳng xOy II. Xác định giá trị các lực. 1. Tại vị trí bánh đai: - Momen gây xoắn: N ( Kw) 10 M D  9550 ( N .m)  9550  382( N .m) n(v / ph) 250 - Lực căng đai: 2M D 2.382 t   1528( N ) D 0,5 3t = 3.1528 = 4584 (N) 2. Tại vị trí bánh răng trụ răng thẳng Z1: - Momen gây xoắn: (Bỏ qua tổn thất do ma sát) MD M1   127,3( N .m) 3 - Lực tiếp tuyến: 2M1 2.127,3 P 1   2546( N ) D1 0,1 - Lực hướng kính: T1  0,364P  0,364.2546  926,7( N ) 1 3. Tại vị trí bánh răng nón Z2: - Momen gây xoắn: ( Bỏ qua tổn thất do ma sát) 2M D M2   254, 7( N .m) 3 - Lực tiếp tuyến: 2M 2 2.254, 7 P2    2830( N ) D2 0,18 - Lực hướng kính : T2  0,364.P2  0,364.2830  1030( N ) 13
- Lực dọc trục: A2  k.P2  0,14.2830  396, 2( N ) - Momen do lực dọc trục gây lên: A2 .D2 144, 2.0,18 M a2    35, 66( N .m) 2 2 2 PHẦN II: VẼ BIỂU ĐỒ MOMEN CHO DẦM SIÊU TĨNH I. Vẽ biểu đồ momen Mxst Cắt bỏ mút thừa và chuyển lực về gần gối lân cận, được một lực và một momen M2 Như vậy ra có dầm liên tục với bậc siêu tĩnh n = 1. 1. Hệ cơ bản hợp lí: Tưởng tượng cắt dời dầm tại vị trí các gối và nối chúng lại bằng một khớp, ta giải phóng được liên kết chống xoay. 2. Hệ tĩnh định tương đương. Đặt tải trọng và mô men liên kết tại khớp. Với điều kiện góc xoay tương đối giữa 2 mặt cắt sát khớp bằng không, ta được hệ tĩnh định tương đương. 3. Phương trình 3 mômen   .a  .b  l1.M o  2(l1  l2 ) M1  l2 .M 2  6  1 1  2 2   0  l1 l2  Trong đó: l1 = 4.70 = 280 mm l2 = 2.70=140mm Mo = 0 M2 = 0  1 1    .a  .b    0, 28 198,1 0,14  0,14  32, 43  0,07  6 1 1  2 2   6  2 2   90  l1 l2   0, 28 0,14    Thay vào phương trình 3 mô men và giải ra ta được: M1 = 107,14 N.m 4. Vẽ biểu đồ mô men: - Thay giá trị mô men M1 vào hệ tĩnh định tương đương. - Vẽ biều đồ mômen M1 - Vẽ biểu đồ mômen M2 - Áp dụng nguyên lí cộng tác dụng, vẽ biểu đồ Mxst 14
Biểu đồ Mxst: 2a 2a a a HCB P2 M0 M1 M1 M2 A2 HTDTD T1 198,10 32,43 MP 53,57 53,57 M1 144,53 107,14 MSt X 21,14 107,14 15
II. Vẽ biểu đồ mômen Myst: Cắt bỏ mút thừa và chuyển lực về gối lân cận, được 1 lực và 1 mômen M2. Như vậy ta có dầm liên tục với bậc siêu tĩnh n = 1. 1. Hệ cơ bản hợp lí: Tưởng tượng cắt dời dầm tại vị trí các gối và nối chúng lại bằng một khớp, ta giải phóng được liên kết chống xoay. 2. Hệ tĩnh định tương đương: Đặt tải trọng và mô men liên kết tại khớp. Với điều kiện góc xoay tương đối giữa 2 mặt cắt sát khớp bằng không, ta được hệ tĩnh định tương đương. 3. Phương trình 3 mômen:   .a  .b  l1.M o  2(l1  l2 ) M1  l2 .M 2  6  1 1  2 2   0  l1 l2  Trong đó: l1 = 280mm l2 = 140mm Mo = 0 M2 = 0 1 2   2  0,14  250,37  3  0,14  0,07  214,71 0,175      1    0,07  (267,8  214,71)  0,14   0,07  0,07  267,8  0, 23  1 2  1.a1 2 .b2   2      3  2 6   6   l1 l2   0, 28   1    0,14  89,11 0,07   2   0,14   128,18 Thay vào phương trình 3 mô men và giải ra ta được: M1 = -152,5(N.m) 4. Vẽ biểu đồ mô men: - Thay giá trị mô men M1 vào hệ tĩnh định tương đương. - Vẽ biều đồ mômen M1 - Vẽ biểu đồ mômen M2 - Áp dụng nguyên lí cộng tác dụng, vẽ biểu đồ Myst 16
Biểu đồ Myst: 2a a a a a HCB Ma2 3t M1 M1 M2 M0 T2 HTDTD P1 89,11 214,71 MP 267,8 250,37 114,37 152,5 76,25 76,25 M1 152,5 165,36 138,46 MSt Y 153,43 174,12 17
III. Vẽ biểu đồ mômen Mzst: Dựa vào sơ đồ lực, ta vẽ được biểu đồ Mzst trên hình vẽ: 2a a a a a Md M2 M1 HTDTD 254,7 MSt Z 127,3 127,3 18
Phần III: Xác Định Đường Kính Trục Siêu Tĩnh Dựa vào các biểu đồ mômen trên hình vẽ ta có: A E D B F C 144,53 18,64 MSt X 21,14 107,14 165,36 138,46 152,5 MSt Y 153,43 174,12 254,7 MSt Z 127,3 127,3 1. Xác định mặt cắt nguy hiểm: Theo thuyết bền thế năng biến đổi hình dạng cực đại, ta có: M td  M x  M y  0,75.M z2 2 2 Áp dụng công thức ta có: Tại A: Mtd = 0 19
M td ( Etrai )  144,532  174,122  226, 29 N .m Tại E: M td ( E phai )  144,532  174,122  0, 75.254, 7 2  316 N .m M td ( Dtrai )  18, 642  153, 432  0, 75.254, 7 2  269,3 N .m Tại D: M td ( Dphai )  18, 642  153, 432  0, 75.127,32  189,8 N .m Tại B: M td ( B)  107,14  152,5  0, 75.127,3  216,5 N .m 2 2 2 M td ( Ftrai )  21,142  165,362  0, 75.127,32  199,86 N .m Tại F: M td ( Fphai )  21,142  165,362  166, 7 N .m Tại C: Mtd = 0 Mặt cắt nguy hiểm là mặt cắt có Mtd lớn nhất. Theo kết quả tính trên, ta có mặt cắt nguy hiểm là mặt đi qua điểm Ephai có Mtd = 316(N.m) 2. Xác định đường kính: Theo điều kiện bền ta có: M td M td  td    [ ] Wx 0,1.d 3 Cho nên: max M td 316 d3 3  0, 0165(m)  16,5(mm) [ ] 70.106 20