
Bài tập Toán rời rạc
Đồ thị 1
1. Xét P(m, n)là câu ”Đồ thị đầy đủ nđỉnh Kncó đúng mcạnh”, ở đây miền giá trị của
cả hai biến là tập số nguyên dương. Xác định giá trị chân lý của các khẳng định sau:
(a) P(2,2) = T hay F
(b) P(3,3) = T hay F
(c) P(4,4) = T hay F
(d) ∃m∀n P (n, m) = T hay F
(e) ∀n∃m P (n, m) = T hay F
(f) ∃n P (n, 2n) = T hay F
2. Xét đồ thị G= (V, E). Ta nhắc lại rằng bậc của một đỉnh v∈V, ký hiệu deg(v), là số
cạnh liên thuộc với nó.
(a) Chứng minh rằng
2|E|=∑
v∈V
deg(v)
(b) Chứng minh rằng số đỉnh bậc lẻ của Gluôn là số chẵn.
(c) Giả sử Dvà dlà bậc lớn nhất và bậc nhỏ nhất của G. Chứng minh rằng
d≤2|E|
|V|≤D.
3. Nhắc lại rằng tô màu đồ thị là một cách gán màu cho mỗi đỉnh của đồ thị sao cho hai
đỉnh kề nhau có màu khác nhau.
Bổ đề (Sai).Xét Glà một đồ thị có bậc lớn nhất không lớn hơn k. Nếu Gcó một đỉnh
nhỏ hơn k, vậy Gcó thể tô bằng kmàu.
(a) Hãy đưa ra một phản ví dụ cho Bổ đề Sai khi k= 1.
(b) Hãy chỉ ra chính xác câu nào sai trong chứng minh sau đây của Bổ đề Sai:
Chứng minh. Chứng minh bằng quy nạp theo số đỉnh n.
Giả thiết quy nạp: P(n)là mệnh đề: Xét một đồ thị Gcó nđỉnh sao cho bậc lớn nhất
của nó không vượt quá k. Nếu Gcó một đỉnh có bậc nhỏ hơn k, thì Gtô được bằng k
màu.
Bước cơ sở: (n= 1) Gcó chỉ một đỉnh, vậy nó tô được bằng 1màu. Vậy P(1) đúng.
Bước quy nạp: Ta giả sử P(n)đúng, xét Gn+1 là đồ thị với n+ 1 đỉnh và bậc lớn
nhất không vượt quá k. Ta giả sử Gn+1 có một đỉnh vcó bậc nhỏ hơn k. Ta cần chứng
minh Gn+1 có thể tô bằng kmàu.
Để làm điều này, trước hết ta xét đồ thị Gnlà đồ thị tạo từ Gn+1 bằng cách xóa đỉnh v
và các cạnh liên quan. Việc xóa đỉnh vgiảm bậc của mọi đỉnh kề với vđi 1. Vậy trong
Gncác đỉnh này có bậc nhỏ hơn k. Và bậc lớn nhất của Gnvẫn không vượt quá k. Vậy
1
Gnthỏa mãn các điều kiện của giả thiết quy nạp P(n). Ta kết luận rằng Gncó thể tô
bằng kmàu.
Bây giờ, kmàu của đồ thị Gndùng để tô mọi đỉnh của đồ thị Gn+1 trừ đỉnh v. Vì vcó
bậc nhỏ hơn k, có ít hơn kmàu được gán cho các đỉnh kề với v. Vậy trong số kmàu có
thể, sẽ có một màu không được dùng cho các nút kề với v, và màu này có thể được gán
cho vđể tô Gn+1 bằng kmàu.
4. Một đồ thị có độ rộng mnếu các đỉnh có nó có thể được sắp xếp thành dãy
v1, v2,· · · , vn
sao cho mỗi đỉnh vicó cạnh nối với nhiều nhất là mđỉnh đứng trước nó (Đỉnh vjđứng
trước vinếu j < i.) Dùng quy nạp để chứng minh rằng mọi đồ thị với độ rộng nhỏ hơn
hoặc bằng mđều có thể tô bằng (m+ 1) màu.
5. Đồ thị phẳng là đồ thị có thể vẽ trên mặt phẳng sao cho các đường cong biểu diễn cạnh
hoặc không giao nhau hoặc chỉ giao nhau ở các đỉnh chung.
(a) Chỉ ra rằng đồ thị con của một đồ thị phẳng cũng là đồ thị phẳng.
(b) Ta biết rằng mọi đồ thị phẳng phải có một đỉnh có bậc không lớn hơn 5. Hãy chứng
minh bằng quy nạp rằng mọi đồ thị phẳng có thể tô không dùng quá 6màu.
6. Hai đồ thị gọi là đẳng cấu nếu chúng giống hệt nhau về cấu trúc nhưng chỉ khác nhau
nhãn của đỉnh. Nói một cách chính xác, hai đồ thị G= (V, E)và H= (W, F )đẳng cấu,
và viết G∼
=H, nếu có một song ánh f:V→Wsao cho:
{x, y} ∈ Enếu và chỉ nếu {f(x), f(y)} ∈ F
với mọi x, y ∈V.
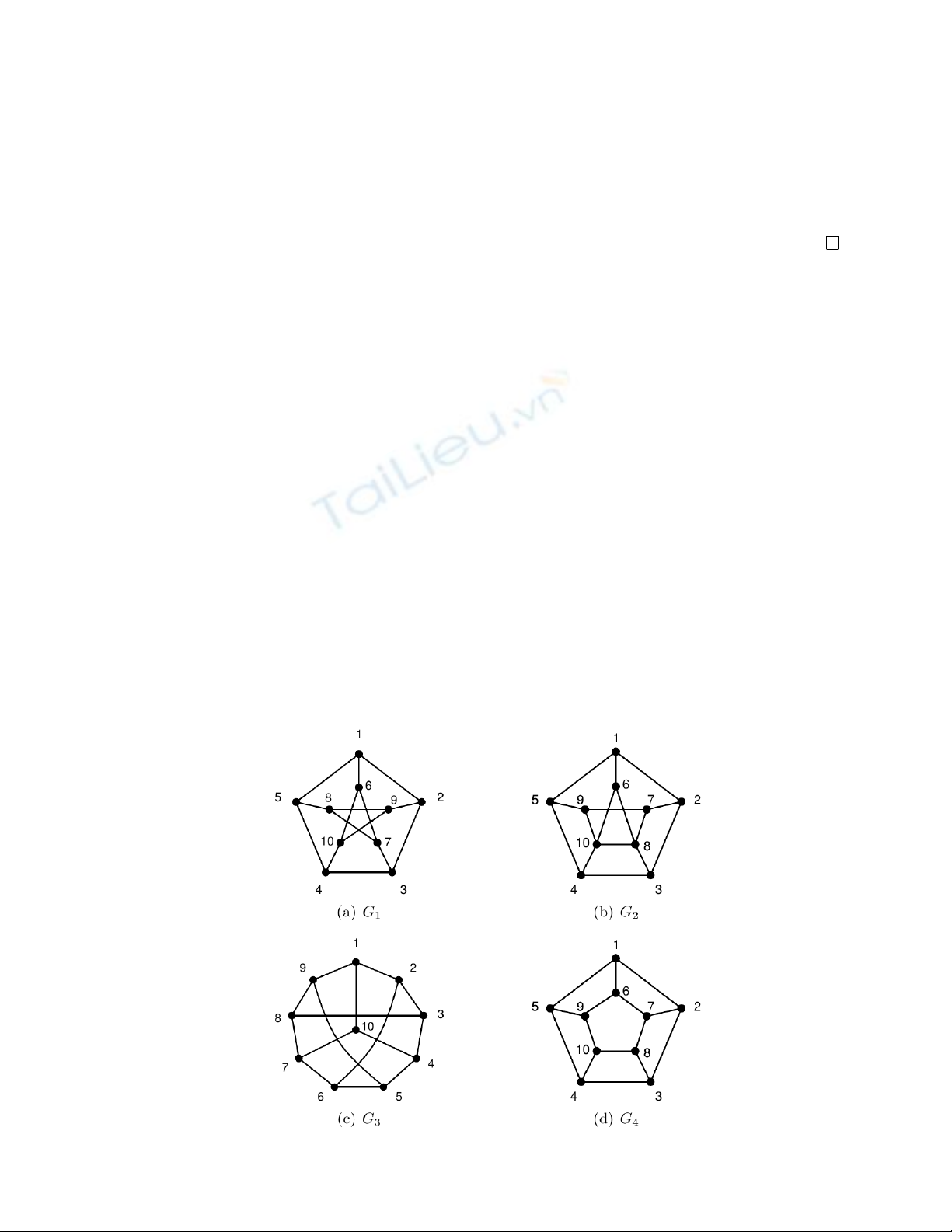
Những cặp đồ thị nào từ bốn đồ thị dưới đây đẳng cấu với nhau? Tại sao?
2
7. Để hiện đại hóa phương pháp giảng dạy, số giờ lên lớp của môn Toán rời rạc bị giảm đi,
thay vào đó mỗi sinh viên phải tham gia vào một số nhóm tự học. Mỗi nhóm tự học này
sẽ phải đề cử một sinh viên đại diện cho nhóm để trình bày một nội dung nghiên cứu
trước lớp. Yêu cầu bắt buộc là một sinh viên chỉ đại diện cho một nhóm. Làm thế nào
để chọn đại diện từ mỗi nhóm để đảm bảo yêu cầu này?
(a) Mô hình bài toán lựa chọn đại diện bằng ghép cặp.
(b) Danh sách đăng ký nhóm của sinh viên cho thấy rằng không có sinh viên nào là
thành viên của hơn 4nhóm và mỗi nhóm đều có ít nhất 4sinh viên. Điều này có
đảm bảo được rằng luôn có cách chọn đại diện thích hợp không? hãy giải thích.
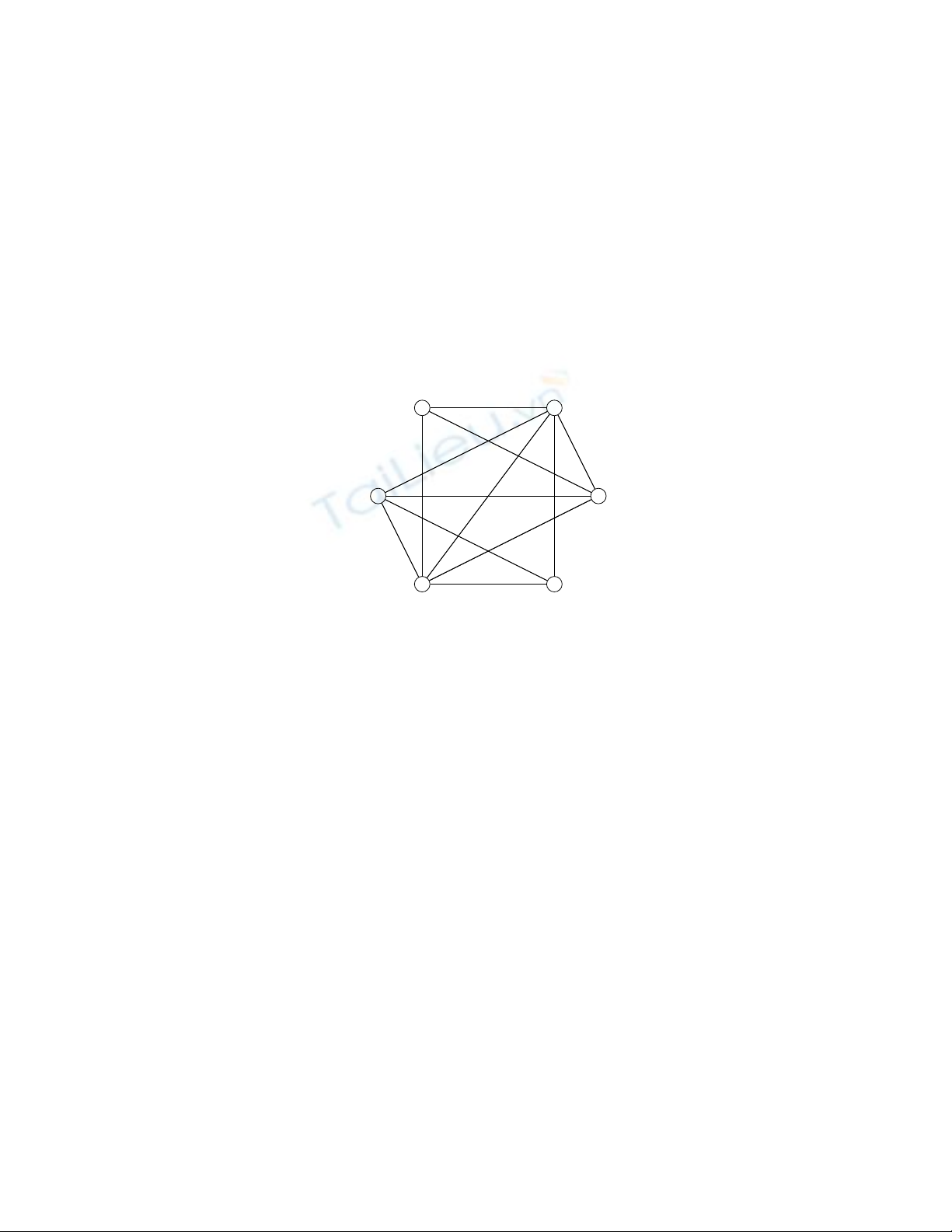
8. Xét đồ thị sau:
.......
(a) Đường kính của đồ thị này bằng bao nhiêu?
(b) Đồ thị này có phải đồ thị phẳng không? Giải thích câu trả lời của bạn.
(c) Số màu ít nhất cần thiết để tô đồ thị trên là bao nhiêu? Giải thích câu trả lời của
bạn.
9. Chứng minh hoặc bác bỏ rằng trong mọi đồ thị với n≥2đỉnh luôn có hai đỉnh cùng
bậc.
3


























