z
y
x
z
y
CH NG 6 : BÀI TOÁN PH NG TRONG T A Đ DESCARTESƯƠ Ẳ Ọ Ộ
6.1. HAI TR NG H P C A BÀI TOÁN PH NGƯỜ Ợ Ủ Ẳ
I. Khái ni m :ệ
Trong nhi u bài toán k thu t, v t th ch u l c ch gây nên bi nề ỹ ậ ậ ể ị ự ỉ ế
d ng hay ng su t trong 1 m t ph ng (M t ph ng này đ c qui c làạ ứ ấ ặ ẳ ặ ẳ ượ ướ
m t ph ng oxy). Các bài toán này đ c g i là các bài toán ph ng.ặ ẳ ượ ọ ẳ
Bài toán ph ng chia ra 2 lo i :ẳ ạ
1. Bài toán ng su t ph ng : N u ch t n t i ng su t trong m tứ ấ ẳ ế ỉ ồ ạ ứ ấ ặ
ph ng xoy.ẳ
2.Bài toán bi n d ng ph ng : N u ch t n t i bi n d ng trong m tế ạ ẳ ế ỉ ồ ạ ế ạ ặ
ph ng xoy.ẳ
Hai bài toán này khác nhau v m t v t lý song r t gi ng nhau về ặ ậ ấ ố ề
m t toán h c.ặ ọ
Gi i bài toán ph ng v m t toán h c đ c đ n gi n r t nhi u soả ẳ ề ặ ọ ượ ơ ả ấ ề
v i bài toán không gian.ớ
II. Bài toán ng su t ph ng :ứ ấ ẳ
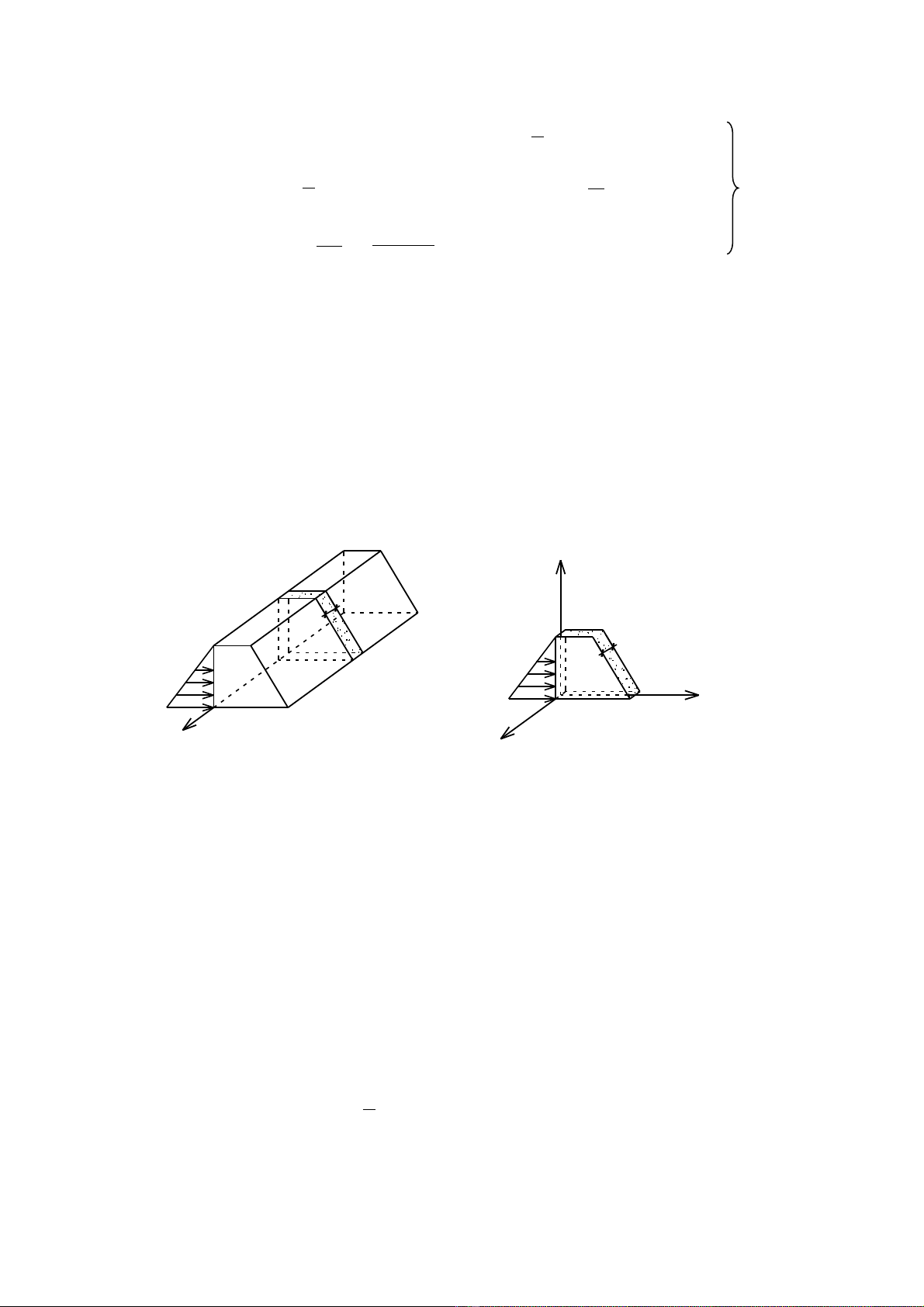
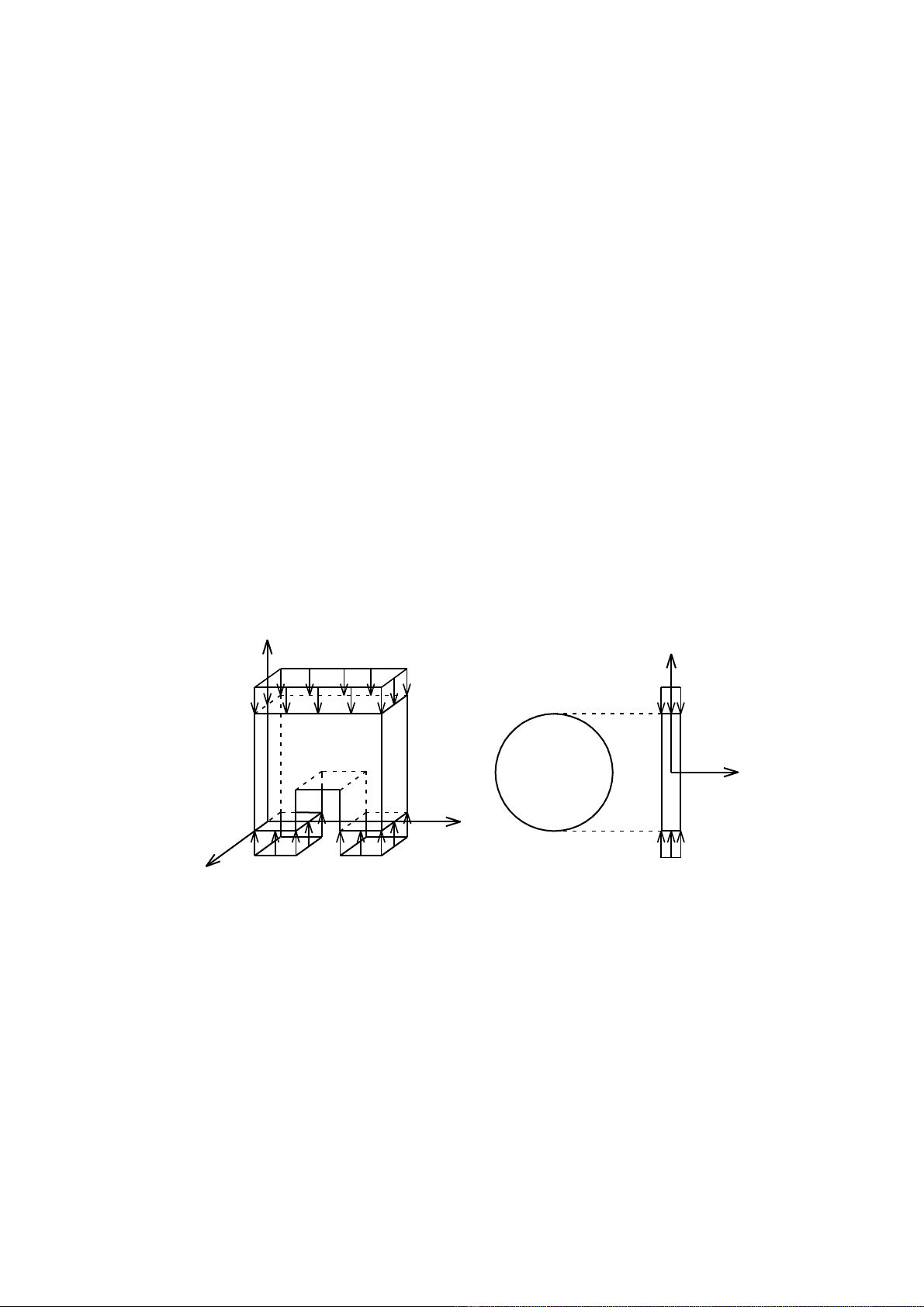
Xét nh ng m t ph ng, ví d t m t ng, đĩa m ng ch u l c phânữ ặ ẳ ụ ấ ườ ỏ ị ự
b đ u trên b dày t m và song song v i m t trung bình nh hình v .ố ề ề ấ ớ ặ ư ẽ
Ta nh n th y m t bên c a t m không có t i tr ng, ng su t làậ ấ ặ ủ ấ ả ọ ứ ấ
h ng theo b dày. Do đó đi u ki n c a bài toán s là :ằ ề ề ệ ủ ẽ
σz = Txz = Tyz = 0 (a)
M t khác, bi n d ng dài theo ph ng b dày là t do nên :ặ ế ạ ươ ề ự
εz ≠ 0 (b)
Các đi u ki n (a), (b) là đ nh nghĩa c a bài toán ng su t ph ng.ề ệ ị ủ ứ ấ ẳ
Ân s c a bài toán g m có:ố ủ ồ
Các ng su t : ứ ấ σx, σy, Txy.
Các bi n d ng : ế ạ εx, εy, γxy, εz ≠ 0.
Theo đ nh lu t Hooke, t (a) ta có :ị ậ ừ
42
z
1
y
z
x
1
γxz =γyz = 0 ; εy =
E
1
(σy - µσx)
εx =
E
1
(σx - µσy) ; εz =-
E
µ
(σx + σy) (c)
γxy =
G
Txy
=
E
)1(2
µ
+
Txy
T bi u th c (c) ta có các bi n d ng đ u tính theo 3 n s ng su t làừ ể ứ ế ạ ề ẩ ố ứ ấ
σx, σy, Txy v i E, ớµ là 2 h ng s đàn h i c a v t li u.ằ ố ồ ủ ậ ệ
III. Bài toán bi n d ng ph ng :ế ạ ẳ
Khi tính nh ng v t th hình lăng tr , có chi u dài l n ch u t iữ ậ ể ụ ề ớ ị ả
tr ng không đ i theo chi u dài, ví d đ p ch n, t ng ch u áp l c,ọ ổ ề ụ ậ ắ ườ ị ự
đ ng ng d n, v h m... ta th ng xét 1 đo n v t th có chi u dàiườ ố ẫ ỏ ầ ườ ạ ậ ể ề
b ng 1 đ n v .ằ ơ ị
Nh th , bài toán đ i v i v t th lăng tr tr thành bài toán t mư ế ố ớ ậ ể ụ ở ấ
ph ng nh bi u di n trên hình v sau :ẳ ư ể ễ ẽ
Nh n xét t m b k p gi a chi u dài c a v t th nên không th cóậ ấ ị ẹ ữ ề ủ ậ ể ể
bi n d ng dài theo ph ng b dày z, và m t bên c a t m s ch u nh ngế ạ ươ ề ặ ủ ấ ẽ ị ữ
áp l c pháp tuy n theo ph ng z. Do đó, đi u ki n c a bài toán đ i v iự ế ươ ề ệ ủ ố ớ
t m trong tr ng h p đang xét s là :ấ ườ ợ ẽ
εz = γxz = γyz = 0 (d)
và σz ≠ 0 (e)
Các đi u ki n (d), (e) là đ nh nghĩa c a bài toán bi n d ng ph ng. ề ệ ị ủ ế ạ ẳ
n s c a bài toán g m có:Ẩ ố ủ ồ
Các ng su t : ứ ấ σx, σy, Txy, σz≠0
Các bi n d ng : ế ạ εx, εy, γxy.
Theo đ nh lu t Hooke, t (d) ta có :ị ậ ừ
- Các ng su t ti p Txz = Tyz = 0ứ ấ ế
- Còn ng su t pháp ứ ấ σz s đ c tìm t bi u th c ẽ ượ ừ ể ứ εz = 0
εz =
[ ]
)(
1yxx
E
σσσ µ
+−
= 0
V y ậσy = µ(σx + σy).
Quan h gi a các ng su t và các bi n d ng còn s là :ệ ữ ứ ấ ế ạ ẽ
43
εx =
[ ]
)(
1zyx
E
σσσ µ
+−
=
[ ]
)(
1yxy
E
σσσ µ
+−
εx =
−
−
−)
1
12
yx
E
σσ µ
µµ
T ng t ươ ự εy =
−
−
−)
1
12
xy
E
σσ µ
µµ
(*)
γxy =
E
)1(2
µ
+
Txy
Đ t ặE1 =
; µ1 =
µ
µ
−1
(g)
(*)⇔ εx =
1
1
E
(σx - µ1σy) ;
εy =
1
1
E
(σy - µ1σx) ; (f)
γxy =
E
)1(2
µ
+
Txy =
1
1)1(2
E
µ
+
Txy
IV. So sánh và k t lu n chung :ế ậ
1. Trong c 2 bài toán ph ng, các n s chính v ng su t và vả ẳ ẩ ố ề ứ ấ ề
bi n d ng là nh nhau : ế ạ ư σx, σy, Txy, εx, εy, γxy.
→ Nh ng ng su t hay bi n d ng còn l i đ u có th bi u di nữ ứ ấ ế ạ ạ ề ể ể ễ
qua các n s chính.ẩ ố
2. Quan h gi a các ng su t hay bi n d ng theo (c) hay (f) làệ ữ ứ ấ ế ạ
hoàn toàn t ng t nh nhau, s khác nhau ch th hi n ch :ươ ự ư ự ỉ ể ệ ở ỗ
- Trong bài toán ng su t ph ng ta dùng các h ng s đàn h i E, ứ ấ ẳ ằ ố ồ µ
còn trong bài toán bi n d ng ph ng ta dùng các h ng s đàn h i Eế ạ ẳ ằ ố ồ 1, µ1
theo cách đ t (g).ặ
3. Do s gi ng nhau v m t toán h c nh v y nên phép gi i c a 2ự ố ề ặ ọ ư ậ ả ủ
bài toán hoàn toàn nh nhau.ư
6.2. CÁC PH NG TRÌNH C B N TRONG BÀI TOÁN PH NG ƯƠ Ơ Ả Ẳ
1. V m t tĩnh h c : Ph ng trình cân b ng Cauchy :ề ặ ọ ươ ằ
y
Tyx
x
x
∂
∂
+
∂
∂
σ
+ fx = 0
y
y
x
Txy
∂
∂
+
∂
∂
σ
+ fy = 0 (6.1)
2. V m t hình h c : Ph ng trình bi n d ng Cauchy :ề ặ ọ ươ ế ạ
εx =
x
u
∂
∂
;
εy =
y
v
∂
∂
; (6.2)
γxy =
x
u
∂
∂
+
y
v
∂
∂
.
44
Các bi n d ng ph i th a mãn đi u ki n liên t c c a bi n d ng,ế ạ ả ỏ ề ệ ụ ủ ế ạ
trong bài toán ph ng đi u ki n này ch còn 1 ph ng trình :ẳ ề ệ ỉ ươ
yx
xy
x
y
y
x
∂∂
∂
=
∂
∂
+
∂
∂
γ
ε
ε
2
2
2
2
2
(6.3)
3. V m t v t lý : Ph ng trình đ nh lu t Hooke.ề ặ ậ ươ ị ậ
a. Bi u th c bi n d ng qua ng su t :ể ứ ế ạ ứ ấ
εx =
E
1
(σx - µσy)
εy =
E
1
(σy - µσx) (6.4)
γxy =
E
)1(2
µ
+
Txy
b. Bi u th c ng su t qua bi n d ng :ể ứ ứ ấ ế ạ
σx =
(εx+ µεy)
σy =
(εy+ µεx) (6.5)
Txy =
)1(2
µ
+
E
γxy
N u gi i bài toán bi n d ng ph ng, ch c n thay E, ế ả ế ạ ẳ ỉ ầ µ b ng Eằ1, µ1.
H tám ph ng trình đ c l p trên, ch a 8 n s là ba ng su t, baệ ươ ộ ậ ứ ẩ ố ứ ấ
bi n d ng và hai chuy n v là m t h khép kín, cho phép ta gi i đ c bàiế ạ ể ị ộ ệ ả ượ
toán.
4. Các đi u ki n biên :ề ệ
a. Đi u ki n biên tĩnh h c :ề ệ ọ
σxl + Tyxm =
∗
x
f
Txyl + σym =
∗
y
f
(6.6)
b. Đi u ki n biên đ ng h c :ề ệ ộ ọ
Trên b m t S c a v t th cho tr c các chuy n v uề ặ ủ ậ ể ướ ể ị o , vo hay các
đ o hàm c a các chuy n v theo các bi n s t a đ . Nghi m chuy n vạ ủ ể ị ế ố ọ ộ ệ ể ị
c a bài toán ph i th a mãn đi u ki n : uủ ả ỏ ề ệ s = uo ; vs= vo .
6.3. PHÉP GI I BÀI TOÁN PH NG THEO NG SU T - HÀMẢ Ẳ Ứ Ấ
NG SU T AIRYỨ Ấ
I. Phép gi i theo ng su t :ả ứ ấ
- Ch n n s chính là các ng su t : ọ ẩ ố ứ ấ σx, σy, Txy.
Các ng su t này ph i th a mãn ph ng trình cân b ng (6.1) .ứ ấ ả ỏ ươ ằ
y
Tyx
x
x
∂
∂
+
∂
∂
σ
= - fx
45
y
y
x
Txy
∂
∂
+
∂
∂
σ
= - fy
Nghi m c a (6.1) s là t ng c a nghi m t ng quát ph ng trìnhệ ủ ẽ ổ ủ ệ ổ ươ
thu n nh t (6.8)ầ ấ
y
Tyx
x
x
∂
∂
+
∂
∂
σ
= 0
y
y
x
Txy
∂
∂
+
∂
∂
σ
= 0 (6.8)
và nghi m riêng c a ph ng trình (6.9)ệ ủ ươ
y
Tyx
x
x
∂
∂
+
∂
∂
σ
= - fx
y
y
x
Txy
∂
∂
+
∂
∂
σ
= - fy (6.9)
- Nghi m riêng c a ph ng trình (6.8) tìm đ c không khó khăn,ệ ủ ươ ượ
nó ph thu c vào d ng c th c a các l c th tích.ụ ộ ạ ụ ể ủ ự ể
Ví d nghi m riêng có th l y là :ụ ệ ể ấ
* σx = 0 ; σy = 0 ; Txy = -Px khi fx = 0 ; fy = P = h ng s .ằ ố
* σx =
2
2
ax
+ bx ; σy = Txy = 0 khi fx = ax + b ; fy = 0
* σx = 0 ; σy = -a
6
3
y
; Txy =
2
2
axy
khi fx = axy , fy = 0.
II. Hàm ng su t Airy :ứ ấ
Đ gi i h (6.1) ta đ a ra m t hàm n m i g i là hàm ng su tể ả ệ ư ộ ẩ ớ ọ ứ ấ
Airy.
Xét h ệph ng trình ph ng trình vi phân thu n nh t (6.8):ươ ươ ầ ấ
0
)8.6(0
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
y
y
x
Txy
y
Tyx
x
x
σ
σ
Đi u ki n c n và đ cho bi u th c p(x,y)dx + q(x,y)dy = du(x,y)ề ệ ầ ủ ể ứ
t c p(x,y)dx + q(x,y)dy là vi phân toàn ph n c a 1 hàm u(x,y) nào đó thìứ ầ ủ
gi a p và q ph i có quan h :ữ ả ệ
x
q
y
p
∂
∂
=
∂
∂
.
- Ph ng trình th (1) c a h (6.8) ươ ứ ủ ệ ⇔
y
Tyx
x
x
∂
∂
−=
∂
∂
σ
T c (ứσx.dy - Txy.dx) là vi phân toàn ph n c a 1 hàm A(x,y) nào đó.ầ ủ
Nên ta có quan h ệσx =
y
A
∂
∂
; Tyx = -
x
A
∂
∂
(a)
T ng t , ph ng trình th 2 : ươ ự ươ ứ
x
Txy
y
y
∂
∂
−=
∂
∂
σ
46