TRƯỜNG ĐẠI HỌC ĐÀ LẠT
KHOA SAU ĐẠI HỌC
.
BÁO CÁO TIỂU LUẬN
PHÂN RÃ HẠT NHÂN
Môn H
ọ
c
: C
Ấ
U TRÚC H
Ạ
T NHÂN
Giảng Viên: TS. PHÙ CHÍ HÒA
Thực Hiện: PHẠM VĂN ĐẠO
Lâm Đồng, tháng 6/2014
MỤC LỤC
CHƯƠNG I: PHÂN RÃ ALPHA ................................................................... 2
I.1 Khái niệm về phân rã alpha ................................................................... 2
I.2 Đặc trưng của phân rã alpha .................................................................. 2
I.2.1 Thời gian bán rã của hạt nhân trước phản ứng .................................... 2
I.2.2 Năng lượng trong phân rã alpha ......................................................... 3
I.2.3 Quãng chạy của hạt alpha ................................................................... 4
I.2.4 Phổ năng lượng .................................................................................. 4
I.3 Cơ chế phân rã alpha ............................................................................. 6
CHƯƠNG II: PHÂN RÃ BETA .................................................................... 8
II.1 Khái niệm về phân rã beta .................................................................... 8
II.2 Các loại phân rã beta ............................................................................ 8
II.3 Đặc trưng trong phân rã beta .............................................................. 11
II.3.1 Phổ năng lượng của beta ................................................................. 11
II.3.2 Các quy tắt chọn lọc trong phân rã beta........................................... 12
II.3 Các tính chất cơ bản của phân rã beta ................................................ 12
CHƯƠNG III: PHÂN RÃ GAMMA ............................................................ 14
III.1 Khái niệm về dịch chuyển gamma và bản chất bức xạ gamma .......... 14
III.2 Đặc trưng của dịch chuyển gamma ................................................... 14
III.2.1 Thời gian sống của hạt nhân phát gamma ...................................... 14
III.2.2 Năng lượng và phổ của bức xạ gamma .......................................... 15
III.2.3 Độ đa cực của lượng tử gamma ..................................................... 15
III.2.3 Các trạng thái isomer ..................................................................... 16
III.3 Quá trình biến hoán nội .................................................................... 16
III.4 Hiện tượng biến hoán tạo cặp ........................................................... 17
TÀI LIỆU THAM KHẢO ............................................................................ 18
1
MỞ ĐẦU
Hiện tượng phóng xạ là quá trình hạt nhân tự động phát ra những hạt để
trở thành hạt nhân khác hoặc thay đổi trạng thái của nó. Hạt nhân chịu sự phóng
xạ gọi là hạt nhân phóng xạ, các tia phát ra gọi là các tia phóng xạ. Hiện tượng
phóng xạ được quan sát đầu tiên bởi nhà khoa học Pháp, Henri Becquerel vào
năm 1896.
Một hạt nhân phóng xạ được đặc trưng bởi: Loại phóng xạ, năng lượng,
chu kỳ bán rã, spin. Một hạt nhân không phóng xạ gọi là hạt nhân bền. Các hạt
nhân phóng xạ tồn tại cùng với hạt nhân bền trong vỏ quả đất, hoặc do con
người tạo nên qua việc thực hiện các phản ứng hạt nhân, hoặc do các tia vũ trụ
bắn phá vào các hạt nhân bền trong khí quyển, hoặc do các vụ nổ nguyên tử…
Hiện tượng phóng xạ là một quá trình thống kê. Các hạt nhân như nhau
nhưng chúng sẽ phóng xạ tại những thời điểm khác nhau. Hiện tượng phóng xạ
xảy ra bên trong hạt nhân, không phụ thuộc vào tác nhân lý hóa bên ngoài.
Chuyên đề này được viết trên cơ sở tổng hợp các kiến thức cơ bản về các tia bức
xạ α, β, γ trong các sách và giáo trình vật lý hạt nhân liên quan.
2
CHƯƠNG I: PHÂN RÃ ALPHA
I.1 Khái niệm về phân rã alpha
Là hiện tượng hạt nhân (ZXA) tự động phát ra alpha (2He4) và trở thành hạt
nhân con (Z-2YA-4)
ZXA → 2He4 + Z-2YA-4 (1.1)
Điều kiện để X phân rã α
- Khối lượng MX > mα + MY
- Năng lượng liên kết Eb = [mα + MY – MX]c2 < 0
Năng lượng phân rã Eα = |Eb| = Kα + KY
I.2 Đặc trưng của phân rã alpha
I.2.1 Thời gian bán rã của hạt nhân trước phản ứng
Thời gian bán rã của các hạt nhân phân rã alpha thay đổi trong một dải rất
rộng. Chẳng hạn 82Pb204 T1/2 = 1,4.107năm, 86Rn125 T1/2 = 10-6s. Thời gian bán rã
T1/2 được xác định trực tiếp nhờ phép đo độ suy giảm hoạt độ theo thời gian hoặc
được xác định theo số phân rã trong một đơn vị thời gian hay từ quy luật cân
bằng thế kỉ.
Tính chất quan trọng nhất của các hạt nhân phân rã alpha là sự phụ thuộc
rất mạnh của thời gian bán rã vào năng lượng Eα bay ra. Sự phụ thuộc của T1/2
vào E tuân theo định luật Geiger – Nuttall như sau:
E
D
CT
2/1 (1.2)
Trong đó C và D là các hằng số không phụ thuộc vào số khối A mà chỉ phụ
thuộc vào điện tích Z.
Định luật Geiger – Nuttall còn được biểu diễn mối liên hệ giữa quãng
chạy R của hạt alpha và hằng số phân rã λ của hạt nhân phát alpha.
BAR
lg.lg (1.3)
3
Định luật Geiger – Nuttall áp dụng rất tốt cho các hạt nhân chẵn – chẵn.
I.2.2 Năng lượng trong phân rã alpha
Khi so sánh năng lượng phân rã alpha Eα giữa các đồng vị trong cùng một
nguyên tố thì thấy năng lượng Eα giảm khi A tăng. Hiện tượng này đúng khi A <
209 và A > 215. Với A ∊ (209, 215) thì ngược lại. Nhờ tính chất này ta có thể
tiên đoán được năng lượng phân rã alpha đối với các đồng vị chưa biết của cùng
một nguyên tố cho trước.
Năng lượng hạt alpha có thể xác định bằng phổ kế từ hay buồng ion hóa.
Bộ phận chính của phổ kế từ là nam châm điện tập trung các hạt alpha năng
lượng khác nhau ở các vị trí khác nhau. Một bản rất mỏng vật liệu hoạt tính
alpha là nguồn phát alpha còn detector ghi hạt alpha là các tấm phim ảnh hoặc
ống đếm alpha. Độ phân giải năng lượng của phổ kế từ rất cao, có thể đạt đến 5
keV.
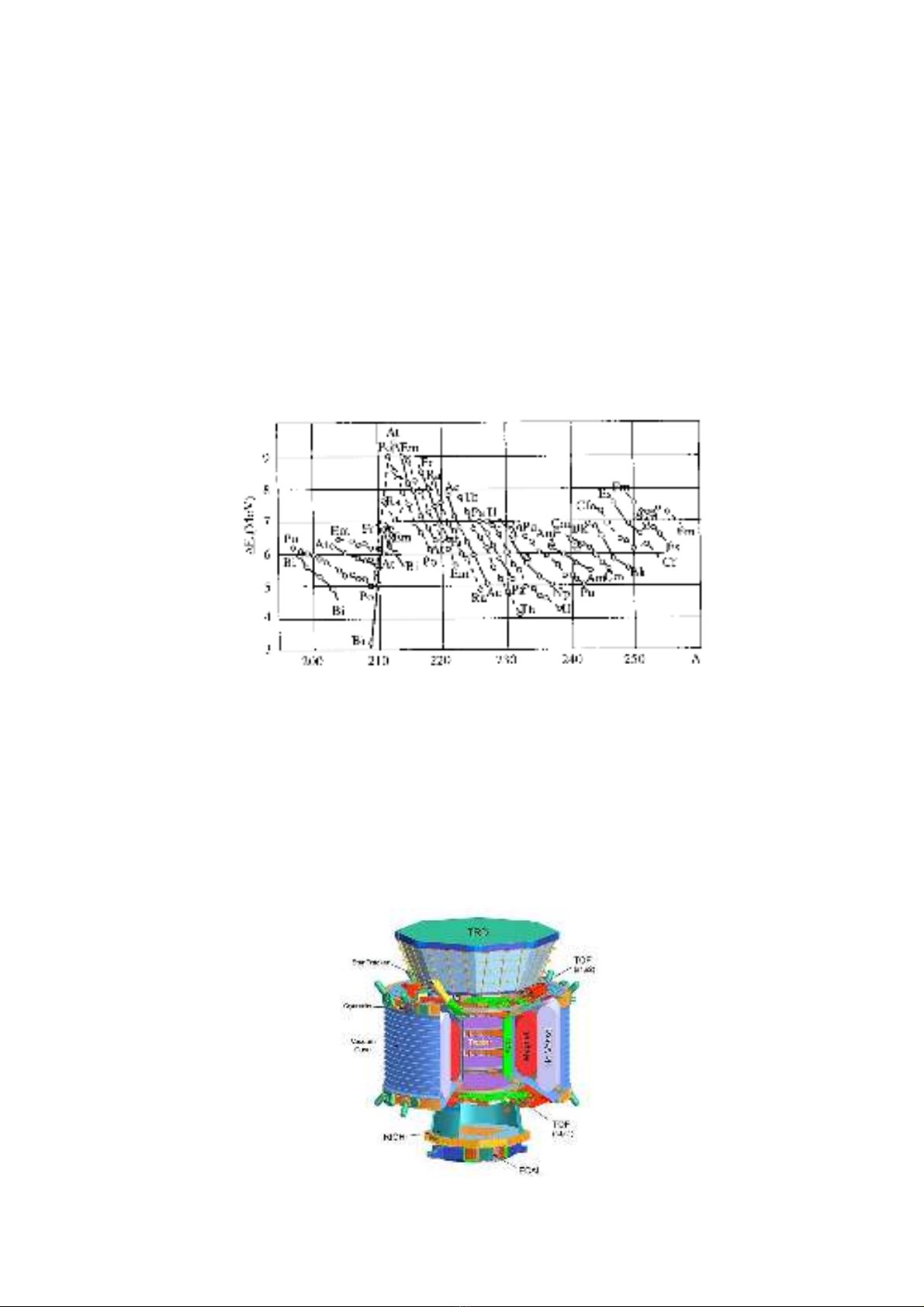
Hình 1.1: Năng lượng phân rã alpha phụ thuộc theo số khối A của các đồng vị
Hình 1.2: Phổ kế từ đo alpha