CÁC BÀI TOÁN CHỌN LỌC
LÊ VIẾT ÂN
(Email: levietan.spt@gmail.com)
1. Đề bài
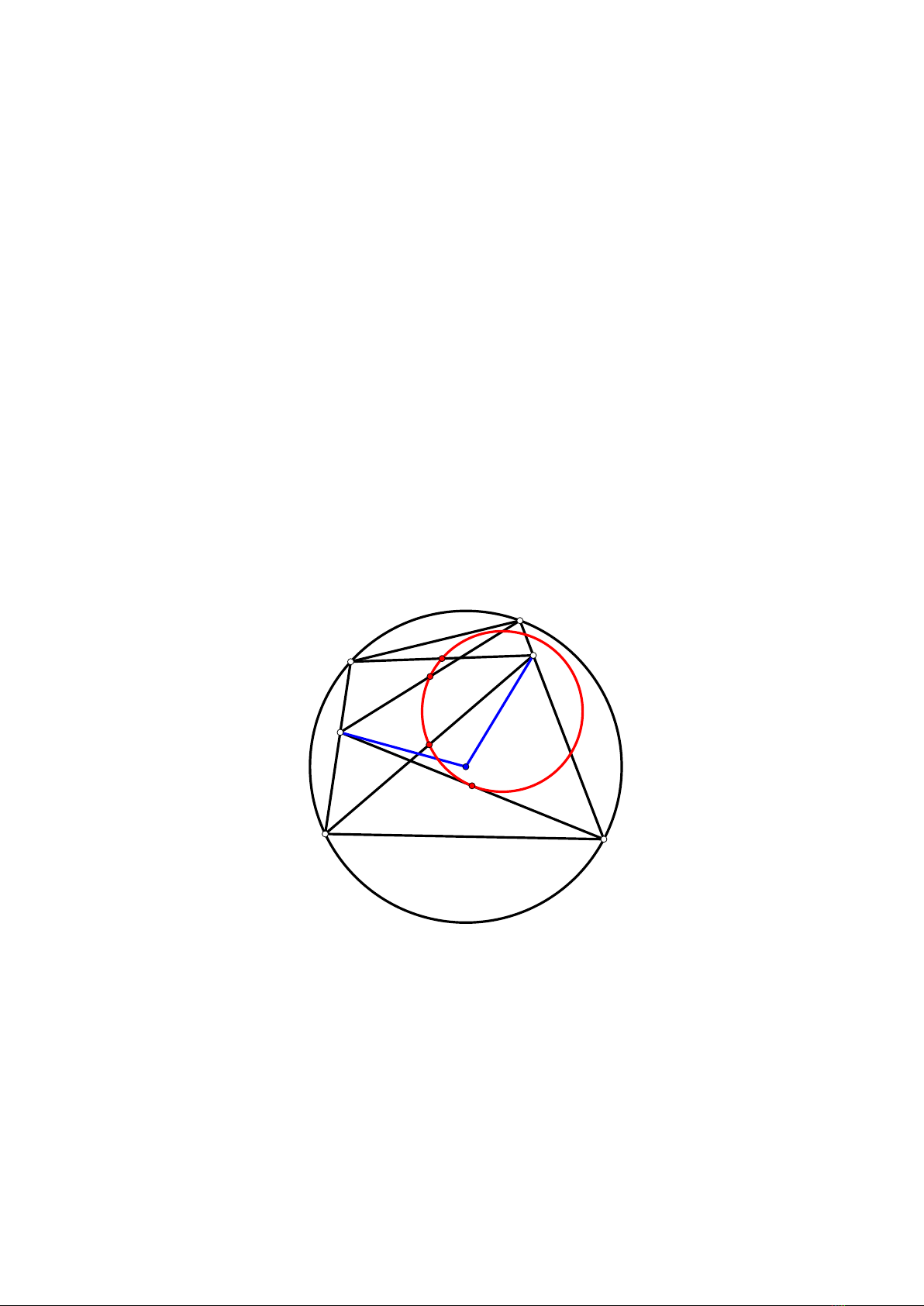
BÀI 1. Cho tứ giác ABCD nội tiếp đường tròn Γcó tâm O. Các điểm Pvà Qtheo thứ tự nằm
trên các cạnh BC, DA. Biết rằng trung điểm của các đoạn thẳng AP, BQ, CQ và DP cùng
nằm trên đường tròn k. Chứng minh rằng OP =OQ.
A
B
C
D
Q
P
O
Γ
k
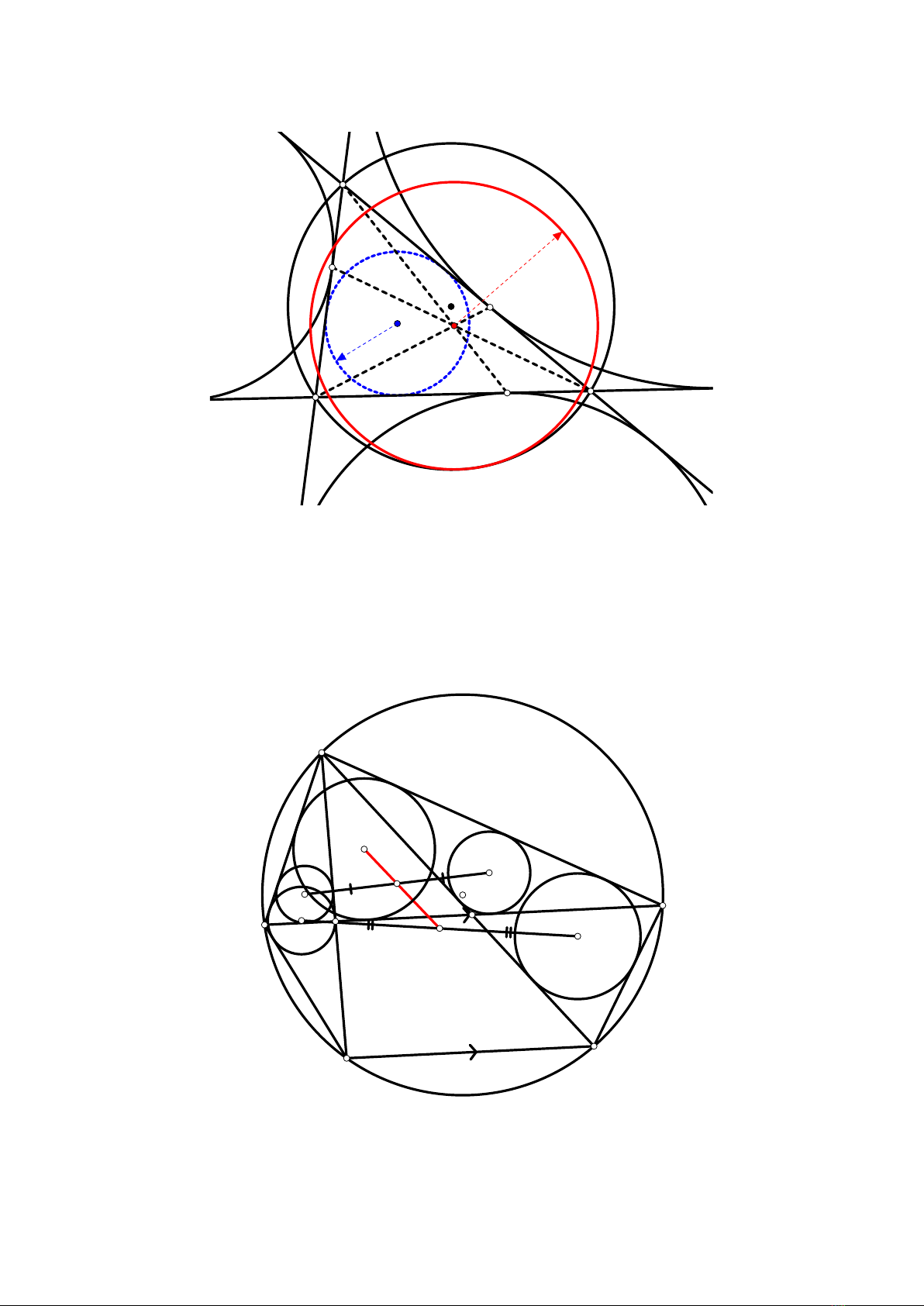
BÀI 2. Cho tam giác ABC nội tiếp đường tròn (O). Gọi rlà bán kính đường tròn nội tiếp và N
điểm Nagel của tam giác. Chứng minh rằng đường tròn tâm N, bán kính 2rtiếp xúc với (O).
2r
A
BC
rN
O
BÀI 3. Cho tam giác ABC nội tiếp đường tròn (O). Các điểm Mvà Nthuộc cung BC
không chứa Acủa (O)sao cho M N kBC. Các đường thẳng AM, AN cắt cạnh BC theo
thứ tự tại P, Q. Gọi I, I1, I2, I3, I4theo thứ tự là tâm đường tròn nội tiếp của các tam giác
ABC, ABP, ABM, ACQ, ACN . Chứng minh rằng đường nối trung điểm của hai đoạn thẳng
I1I3và I2I4đi qua I.
A
BC
M
N
P
Q
I
I1
I2
I3
I4
O
BÀI 4. Cho tam giác ABC và điểm Dkhông thuộc các đường thẳng CA, AB. Các đường tròn
ngoại tiếp các tam giác ABD, ACD theo thứ tự cắt CA, AB tại E, F khác A. Gọi M, N theo
thứ tự là trung điểm của BE, CF ; và gọi Glà điểm đối xứng với Dqua M N. Các đường thẳng
GM, GN theo thứ tự cắt CA, AB tại K, L. Chứng minh rằng đường thẳng nối trung điểm của
các đoạn thẳng BC, KL đi qua điểm G.
A
BC
D
E
FM
N
K
L
G
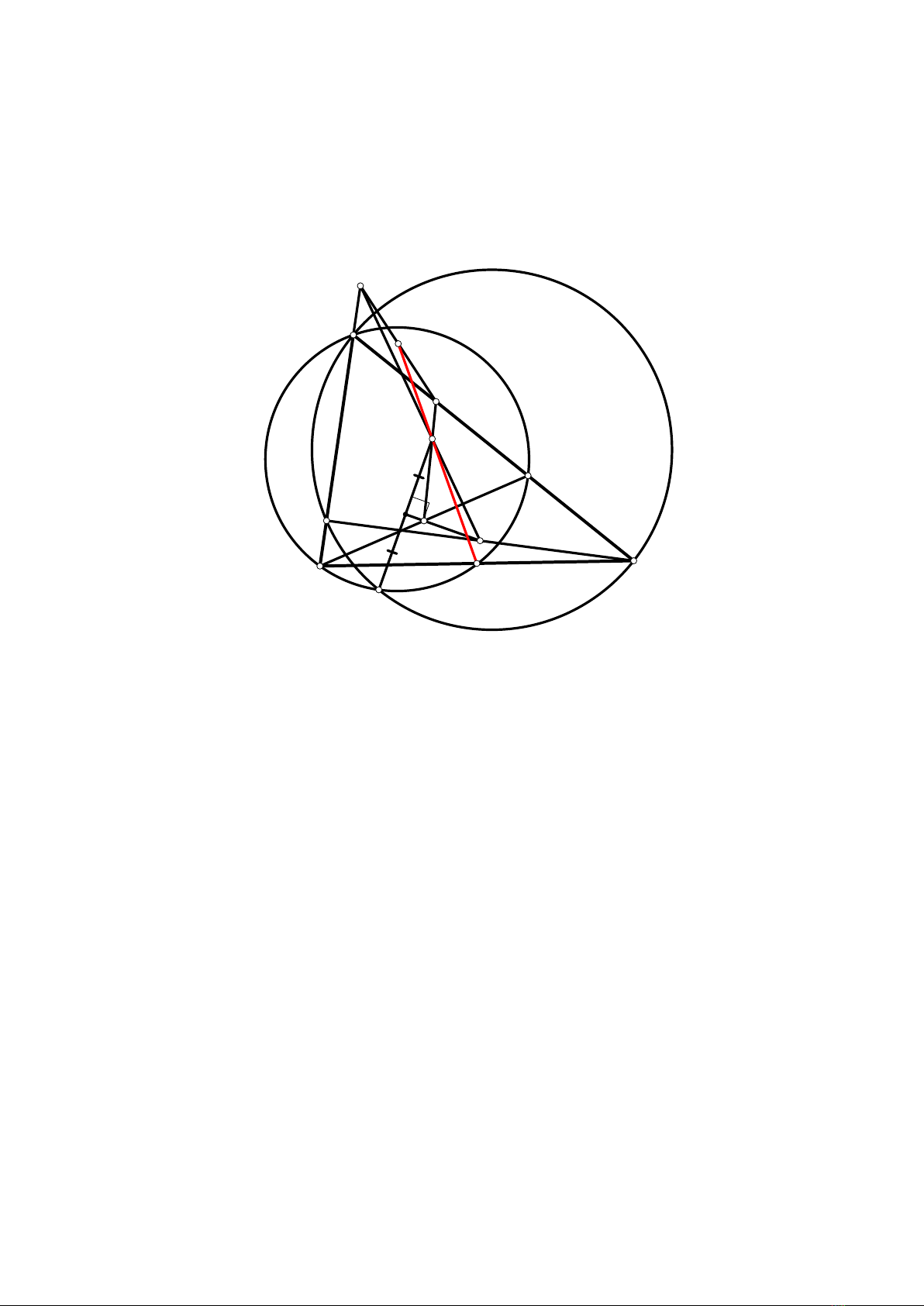
BÀI 5. Cho tam giác ABC, phân giác AD, trung tuyến AM . Điểm Pthuộc đường thẳng BC
(Pkhác B, C, M). (E),(F)là các đường tròn cùng đi qua Ptheo thứ tự tiếp xúc với AB, AC
tại B, C.Qlà giao điểm thứ hai của (E)và (F).AQ theo thứ tự cắt trung trực của AD và
(E),(F)tại Rvà S, T (S, T khác Q). DR cắt AM tại G. Lấy K, L thứ tự thuộc P S, P T sao
cho AK kCG và AL kBG. Chứng minh rằng P K =P L.
A
BC
D
M
P
G
E
F
Q
S
T
K
L
R
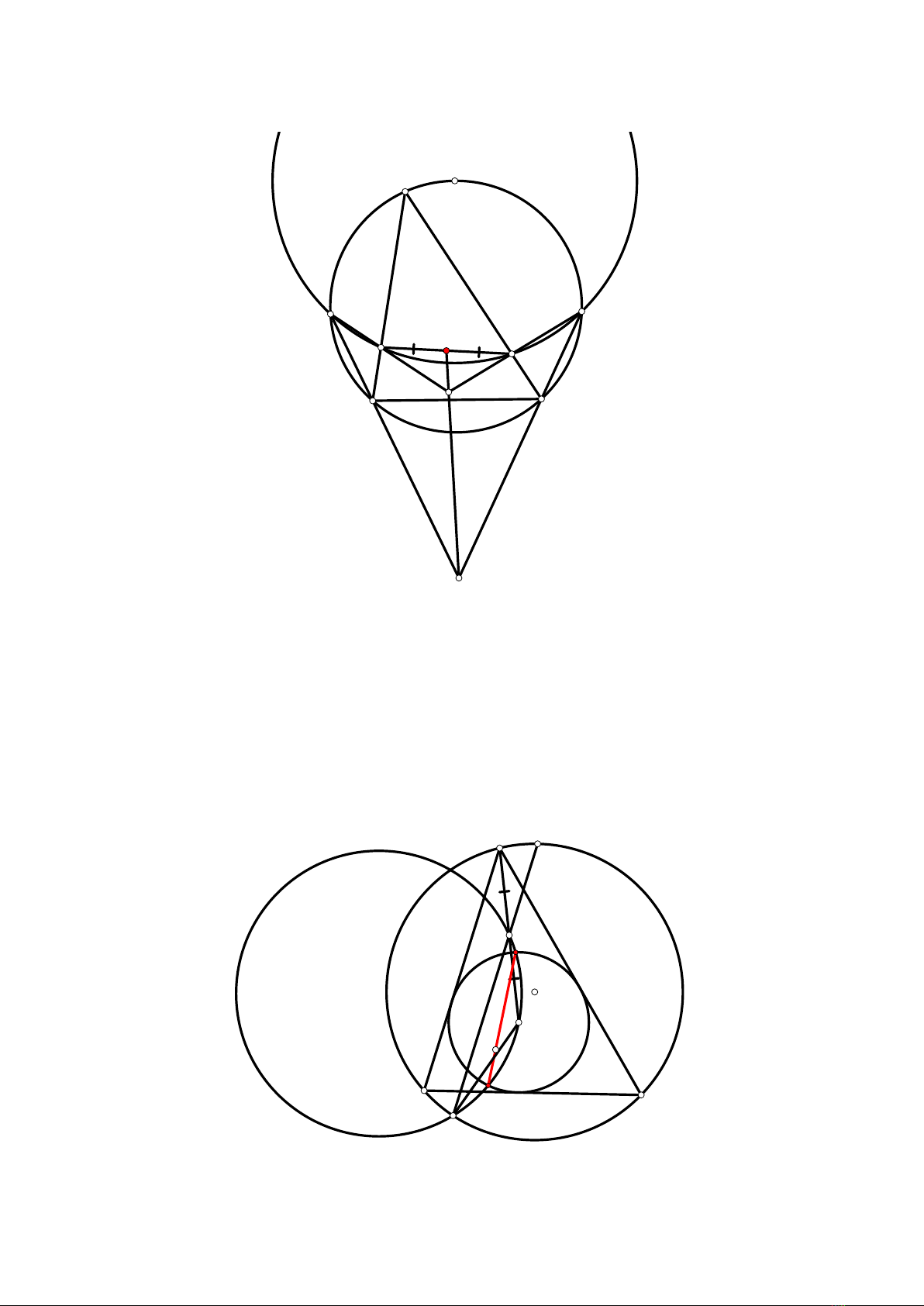
BÀI 6. Cho tam giác ABC nội tiếp đường tròn Ω. Gọi Xlà trung điểm cung BAC của Ω. Một
đường tròn Γvới tâm Xcắt các cạnh AB, AC theo thứ tự tại D, E. Gọi Fvà Glà các giao điểm
của của Ωvà Γsao cho các điểm A, F, B, C và Gnằm trên Ωtheo đúng thứ tự này. Giả sử các
đường thẳng BF và CG phân biệt và cắt nhau tại K; các đường thẳng DF và EG phân biệt và
cắt nhau tại L. Chứng minh rằng KL đi qua trung điểm của DE.
A
B C
X
Γ
Ω
DE
FG
K
L
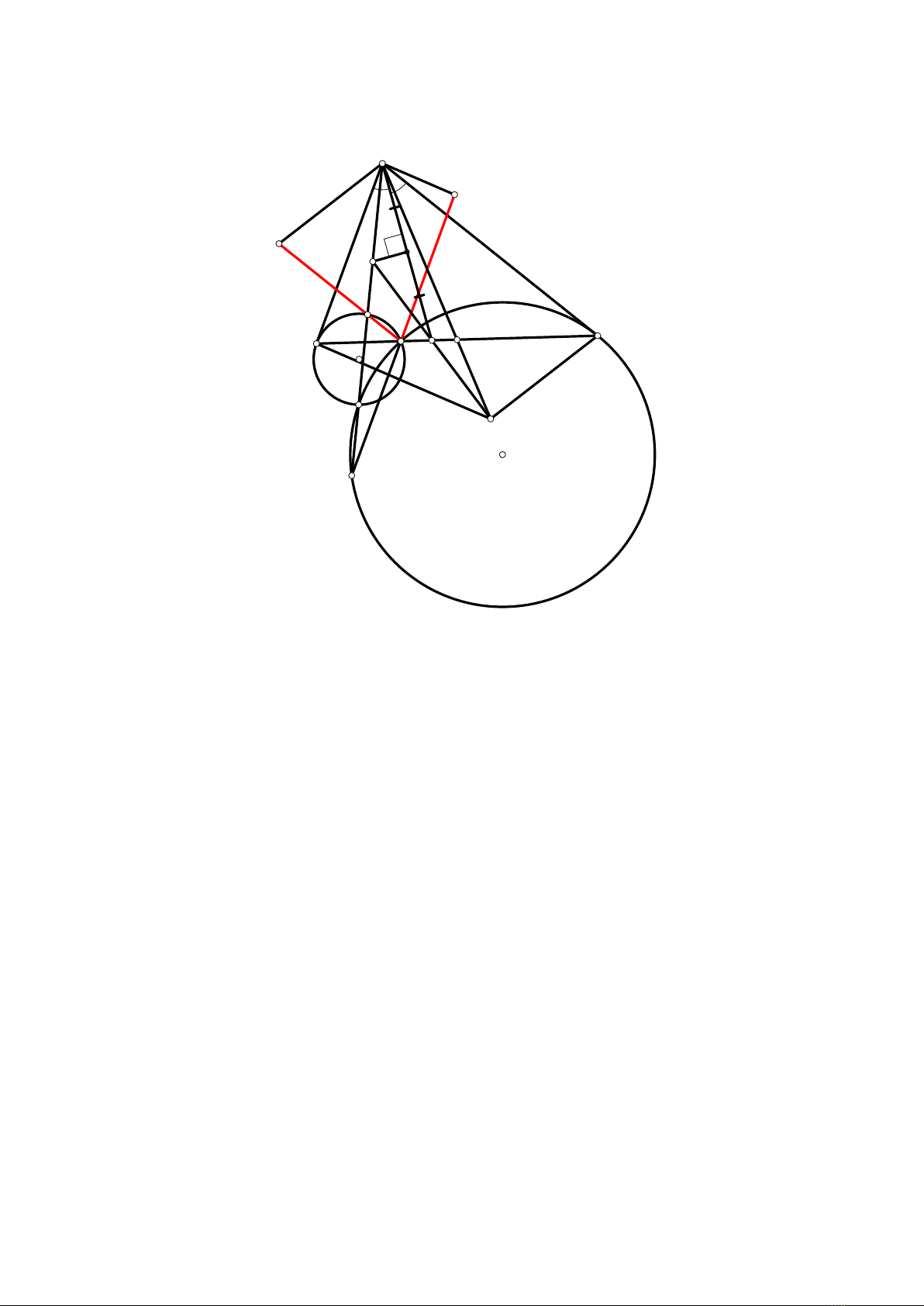
BÀI 7. Cho tam giác ABC với H, (O),(I)theo thứ tự là trực tâm, đường tròn ngoại tiếp và
đường tròn nội tiếp của tam giác. Gọi Plà trung điểm cung BAC của (O); gọi Mlà trung điểm
AI; và gọi Nlà giao điểm thứ hai của (O)và P M. Chứng minh rằng trục đẳng phương của
đường tròn ngoại tiếp tam giác IM N và (I)đi qua điểm H.
A
BC
P
M
O
I
H
N