729
MẶT TRÒN XOAY VÀ MỘT SỐ BÀI TOÁN TRONG THỰC TẾ
Trần Thanh Phong1
1. Khoa Sư phạm. phongtt.khtn@tdmu.edu.vn,
TÓM TẮT
Bài viết trình bày một số kiến thức mặt nón tròn xoay và mặt trụ tròn xoay. Tiếp theo
chúng tôi trình bày một số bài toán trong thực tế được giải quyết bằng cách sử dụng kiến thức
vừa nêu.
Từ khóa: Bài toán thực tế , mặt nón tròn xoay, mặt trụ tròn xoay.
1. GIỚI THIỆU
Trước đây, đa số học sinh tốt nghiệp trung học phổ thông chưa giải quyết được những bài
toán trong thực tế. Giải quyết các bài toán trong thực tế là chủ đề được quan tâm. Gần đây, các
em học sinh được tiếp cận bài toán thực tế và được giáo viên hướng dẫn tìm ra cách giải quyết
bài toán. Trong chương Hình học lớp 12, mặt tròn xoay được trình bày và lý thuyết này có nhiều
ứng dụng trong đời sống hằng ngày. Đặc biệt là lý thuyết mặt nón tròn xoay và mặt trụ tròn
xoay có thể tìm thấy nhiều ứng dụng. Trong bài viết này, chúng tôi tổng hợp lý thuyết toán học
cơ bản về mặt nón tròn xoay và mặt trụ tròn xoay, cùng một số bài toán thực tế được giải quyết
bằng cách sử dụng khéo léo các lý thuyết này.
2. KIẾN THỨC CHUẨN BỊ
Trong mục này, chúng tôi nhắc lại lý thuyết toán học cơ bản về mặt nón tròn xoay và mặt
trụ tròn xoay, lý thuyết này và hình ảnh minh họa có thể tìm thấy trong [2], [3] và [4].
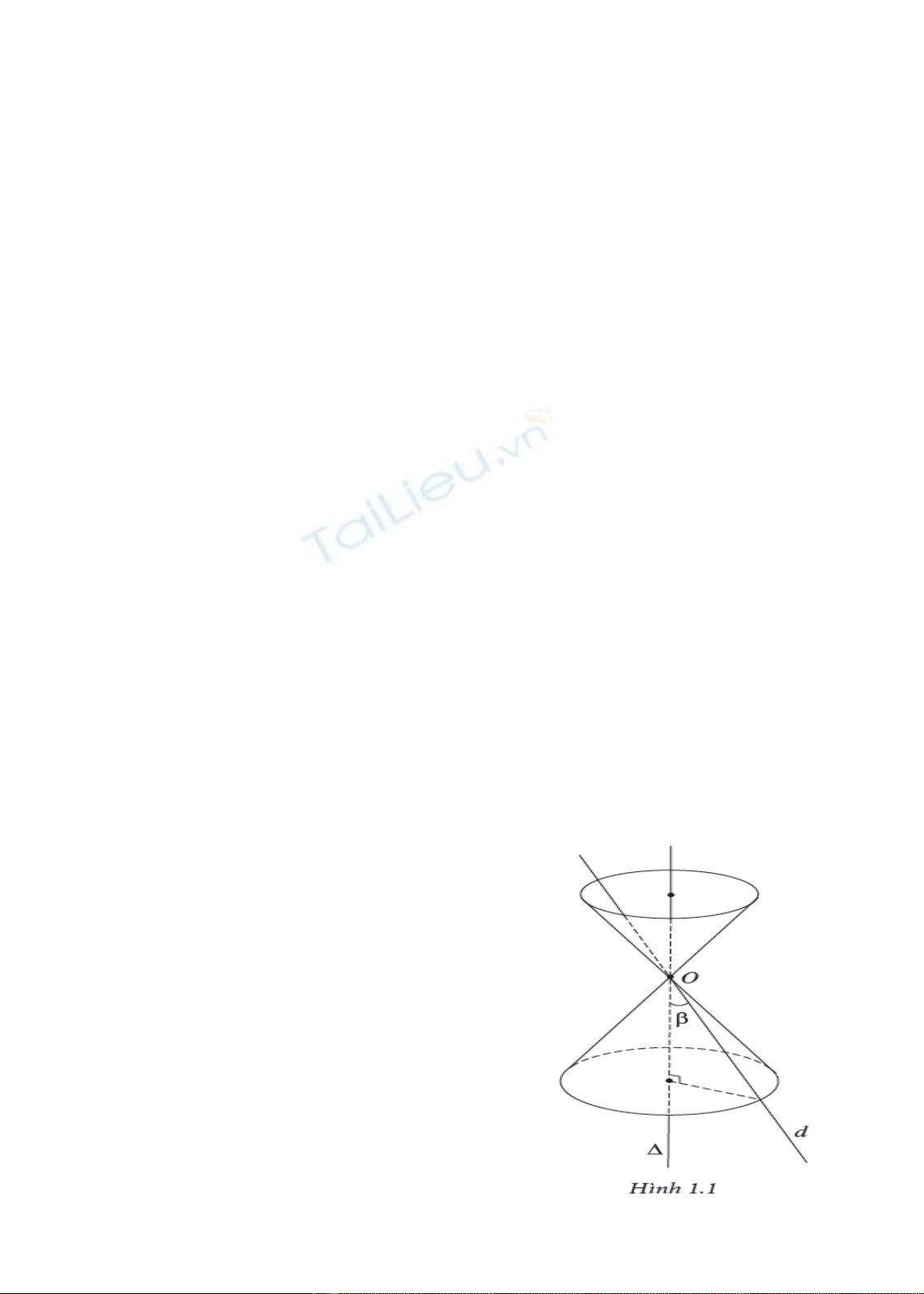
2.1. Định nghĩa mặt nón tròn xoay
Trong mặt phẳng
()P
cho hai đường thẳng
d
và
cắt nhau tại điểm
O
và tạo thành góc
với
00
0 90

. Khi mặt phẳng
quay xung quanh
thì đường thẳng
d
sinh ra một mặt tròn xoay được gọi
là mặt nón tròn xoay đỉnh
O
. Người ta thường gọi mặt
nón tròn xoay là mặt nón. Đường thẳng
gọi là trục,
đường thẳng
d
gọi là đường sinh và góc
2
gọi là góc
ở đỉnh của mặt nón đó (Hình 1.1).
730
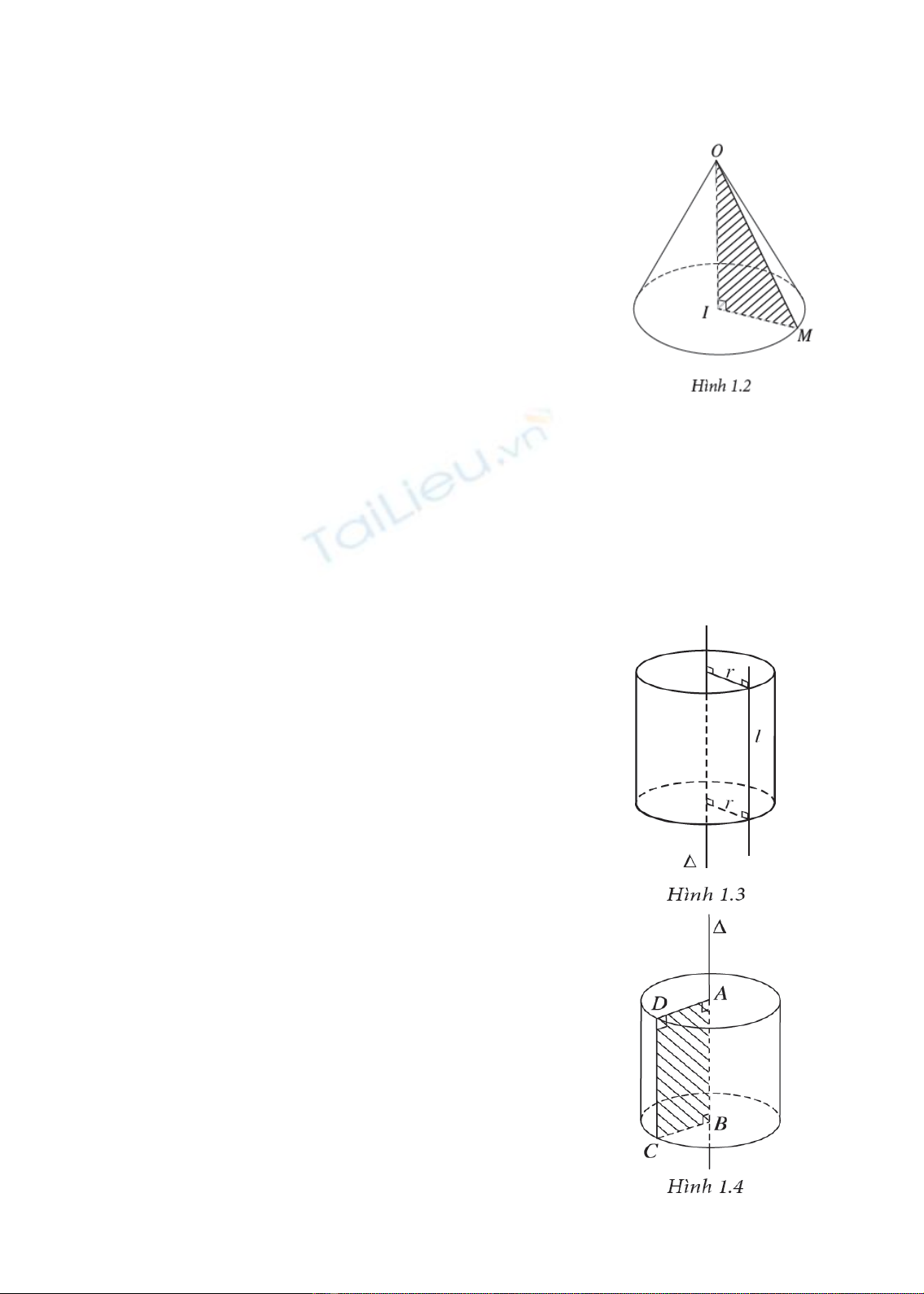
2.2. Hình nón tròn xoay và khối nón tròn xoay
Cho tam giác
OIM
vuông tại
I
(Hình 1.2). Khi quay tam
giác đó xung quanh cạnh góc vuông
OI
thì đường gấp khúc
OMI
tạo thành một hình được gọi là hình nón tròn xoay, gọi tắt
là hình nón.
Hình tròn tâm
I
sinh bởi các điểm thuộc cạnh
IM
khi
IM
quay quanh trục
OI
được gọi là mặt đáy của hình nón, điểm
O
gọi là đỉnh của hình nón. Độ dài đoạn
IO
gọi là chiều cao của
hình nón, đó cũng là khoảng cách từ
O
đến mặt phẳng đáy. Độ
dài
OM
gọi là độ dài đường sinh của hình nón. Phần mặt tròn
xoay được sinh ra bởi các điểm trên cạnh
OM
khi quay quanh
trục
OI
gọi là mặt xung quanh của hình nón đó.
Khối nón tròn xoay là phần không gian được giới hạn bởi một hình nón tròn xoay kế cả hình
nón đó. Người ta còn gọi khối tròn xoay là khối nón. Những điểm thuộc khối nón nhưng không
thuộc hình nón ứng với khối nón ấy được gọi là điểm trong khối nón. Ta gọi đỉnh, mặt đáy, đường
sinh của một hình nón theo thứ tự là đỉnh, mặt đáy, đường sinh của khối nón tương ứng.
Diện tích xung quanh của hình nón tròn xoay bằng nữa tích độ dài đường tròn đáy và độ
dài đường sinh.
Thể tích của khối nón bằng một phần ba diện tích đáy nhân với chiều cao.
2.3. Định nghĩa mặt trụ tròn xoay
Trong mặt phẳng
cho hai đường thẳng
và
l
song
song với nhau, cách nhau một khoảng bằng
r
. Khi quay mặt
phẳng
()P
xung quanh
thì đường thẳng
l
sinh ra một mặt tròn
xoay được gọi là mặt trụ tròn xoay. Người ta thường gọi tắt mặt
trụ tròn xoay là mặt trụ. Đường thẳng
gọi là trục, đường thẳng
l
là đường sinh và
r
là bán kính của mặt trụ đó.(Hình 1.3).
2.4. Hình trụ tròn xoay và khối trụ tròn xoay
Ta hãy xét hình chữ nhật
ABCD
. Khi quay hình chữ nhật
đó xung quanh đường thẳng chứa một cạnh, chẳng hạn cạnh
,
đường gấp khúc
ADCB
tạo thành một hình được gọi là hình trụ
tròn xoay hay còn gọi tắt là hình trụ (Hình 1.4).
Khi quay quanh
AB
, hai cạnh
AD
và
BC
sẽ vạch ra hai
hình tròn bằng nhau gọi là hai đáy của hình trụ, bán kính của chúng
gọi là bán kính của hình trụ. Độ dài đoạn
CD
gọi là độ dài đường
sinh của hình trụ, phần mặt tròn xoay được sinh ra bởi các điểm trên
cạnh
CD
khi quay quanh
gọi là mặt xung quanh của hình trụ.
Khoảng cách
giữa hai mặt phẳng song song chứa hai đáy là
chiều cao của hình trụ.
Khối trụ tròn xoay là phần không gian được giới hạn bởi một
731
hình trụ tròn xoay kể cả hình trụ đó. Khối trụ tròn xoay còn gọi là khối trụ. Những điểm không
thuộc khối trụ được gọi là những điểm ngoài của khối trụ. Những điểm thuộc khối trụ nhưng
không thuộc hình trụ gọi là những điểm trong của khối trụ. Ta gọi mặt đáy, chiều cao, đường
sinh, bán kính của một hình trụ theo thứ tự là mặt đáy, chiều cao, đường sinh, bán kính của khối
trụ tương ứng.
Diện tích xung quanh của hình trụ tròn xoay bằng tích của độ dài đường tròn đáy và độ
dài đường sinh.
Thể tích của khối trụ tròn xoay bằng tích diện tích đáy và chiều cao.
3. MỘT SỐ BÀI TOÁN TRẮC NGHIỆM ỨNG DỤNG THỰC TẾ
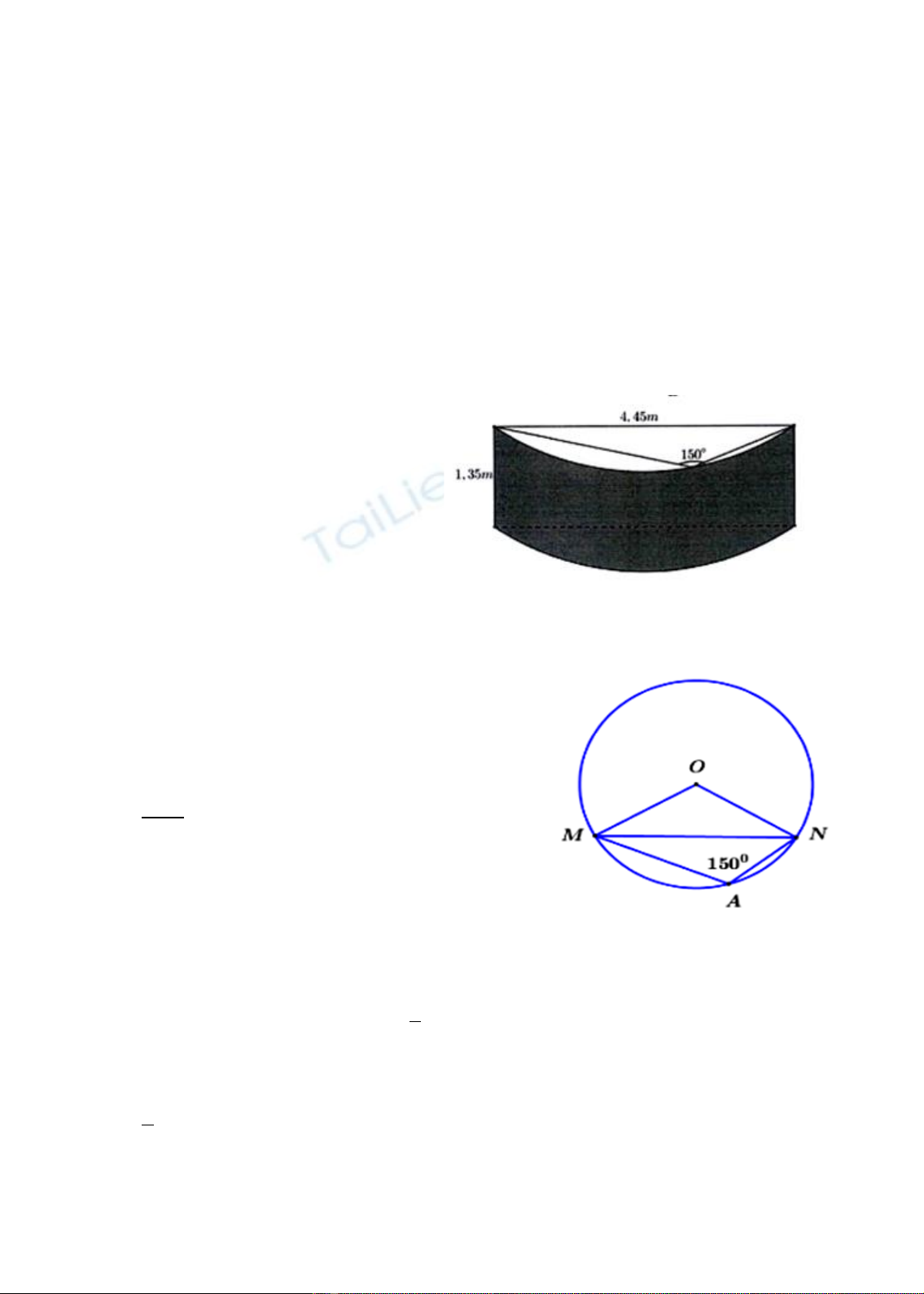
Bài toán 1. ([1] – Câu 44) Ông Bình
làm lan can ban công ngôi nhà của mình
bằng một tấm kính cường lực. Tấm kính đó
là một phần của mặt xung quanh của một
hình trụ như hình bên. Biết giá tiền của
2
1 m
kính như trên là
1.500.000
đồng.
Hỏi số tiền (làm tròn đến hàng nghìn) mà
ông Bình mua tấm kính trên là bao nhiêu?
A. 23.519.000 đồng. B. 36.173.000 đồng. C. 9.437.000 đồng. D. 4.718.000 đồng.
Giải
Giả sử
( )
,OR
là đường tròn đáy của hình trụ.
Áp dụng định lý
sin
trong tam giác
,AMN
với
( )
O
là đường tròn ngoại tiếp tam giác
.AMN
Ta có
2 4,45.
sin
MN RR
A= =
Suy ra diện tích xung quanh của hình trụ là:
( )
2
2 2 .4,45.1,35 12,015 .
xq
S Rh m
= = =
Vì
4,45OM ON MN= = =
nên
OMN
là tam giác đều nên
0
60 .MON =
Do đó diện tích tấm cường lực là:
( )
2
1.
6xq
Sm
Vậy số tiền ông Bình mua tấm kính trên là:
1.12,105 .1500000 9436558
6
(đồng).
Chọn C.
732
Bài toán 2. Một công ty sản xuất bồn đựng
nước hình trụ có thể tích thực
3
1m
với chiều cao
bằng
1m
. Biết bề mặt xung quanh bồn được sơn bởi
loại sơn màu xanh tô như hình vẽ và màu trắng là
phần còn lại của mặt xung quanh; với mỗi mét vuông
bề mặt lượng sơn tiêu hao
0.5
lít sơn. Công ty cần
sơn 10000 bồn thì dự kiến cần bao nhiêu lít sơn màu
xanh gần với số nào nhất, biết khi đo được dây cung
1 BF m=
.
A.
6150
. B.
6250
. C.
1230
D.
1250
Giải
Gọi
r
là bán kính đường tròn đáy
Ta có:
21
.V r h r
= =
.
Xét tam giác
O BF
ta có :
22
2
2
cos( ) 1 2
2
r BF
BO F r
−
= = −
.
Suy ra:
2,178271695BO F
(rad)
Vậy độ dài cung
BF
:
. 1,2289582lr
=
(m), với
BO F
=
(đơn vị đo là rad).
Tổng số lít sơn màu xanh cho mỗi bồn nước là:
. .0.5 0.6144791001T l h==
(lít).
Vậy tổng số sơn cần cho
10000
bồn
6145S
(lít)
Chọn A.
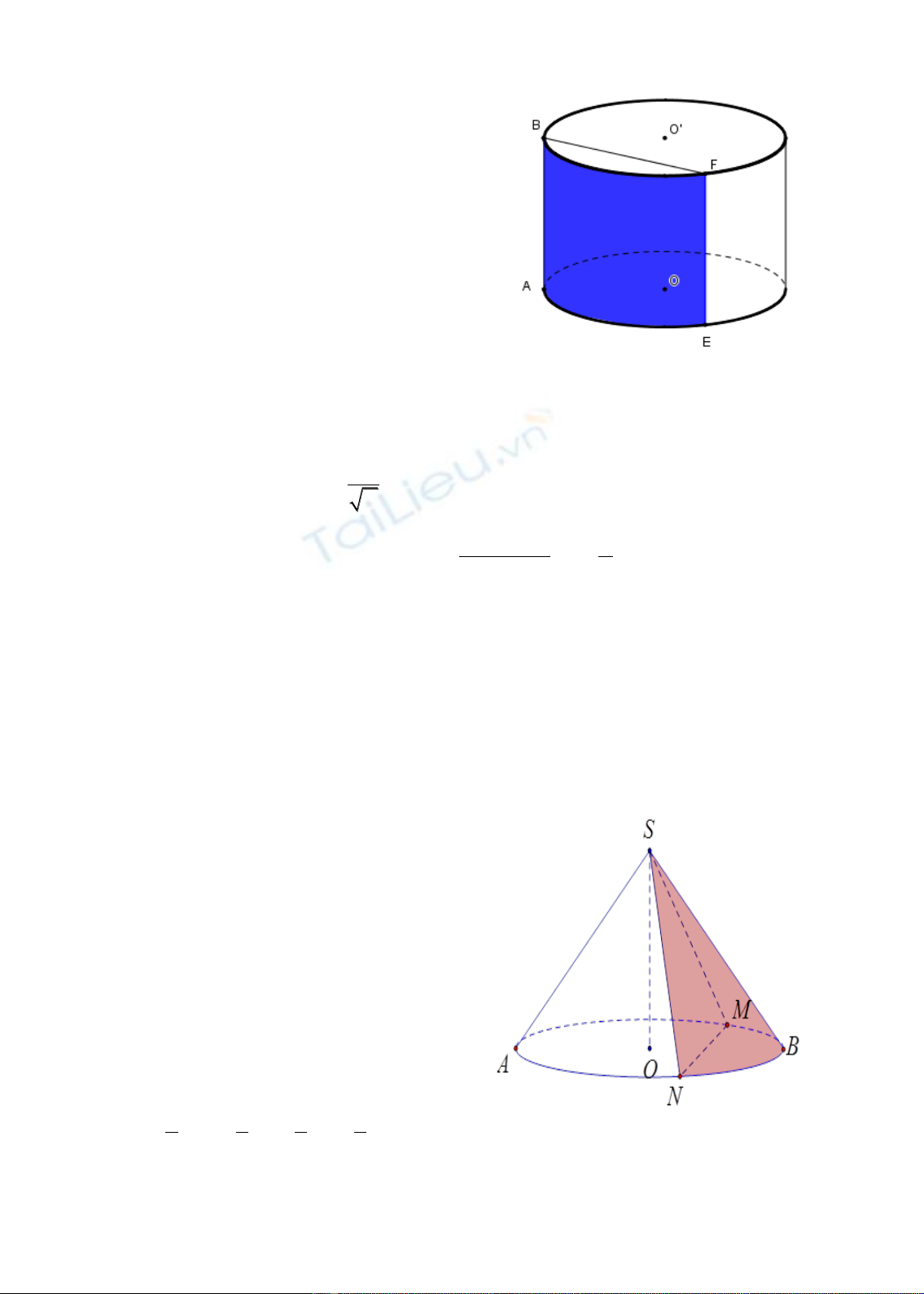
Bài toán 3. Cổ động viên bóng đá của đội
tuyển Indonesia muốn làm một chiếc mũ có dạng
hình nón sơn hai màu Trắng và Đỏ như trên quốc
kỳ. Giả thiết rằng thiết diện qua trục của hình nón
là tam giác vuông cân, S là đỉnh, AB là đường
kính đường tròn đáy và O là tâm đường tròn đáy.
Cổ động viên muốn sơn màu Đỏ ở bề mặt phần
hình nón có đáy là cung nhỏ
MBN
, phần còn lại
là của hình nón sơn màu Trắng. Tính tỉ số phần
diện tích hình nón được sơn màu Đỏ với phần
diện tích sơn màu Trắng.
A.
2
7
. B.
2
5
. C.
1
4
. D.
1
3
.
Giải
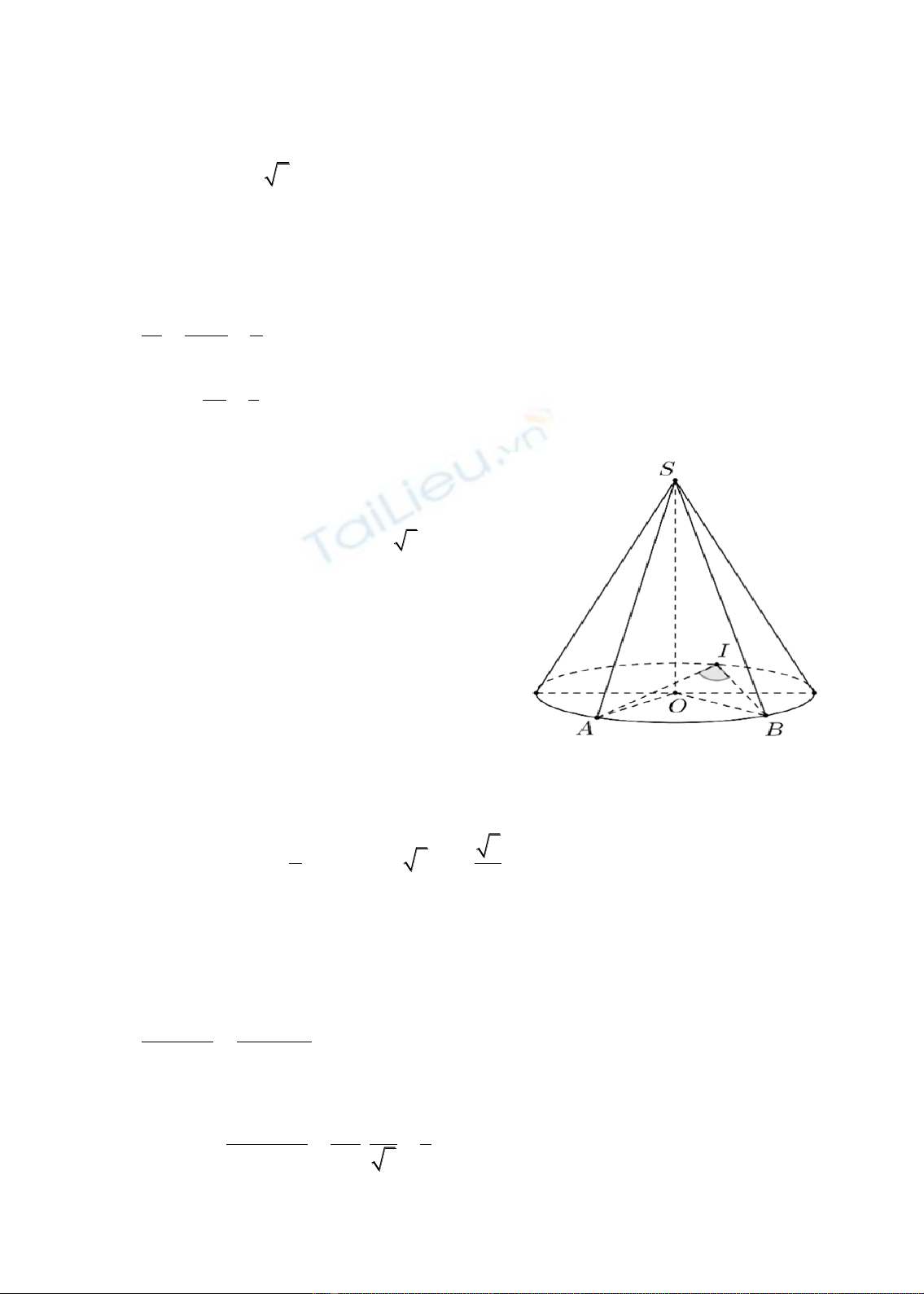
733
Do tam giác
SAB
vuông cân tại S nên
SO OA OB r= = =
(Với
r
là bán kính đường tròn đáy).
Suy ra:
2SM r MN==
.
Do dó tam giác
OMN
vuông cân tại
O
.
Gọi
S
là diện tích xung quanh của hình nón,
d
S
là diện tích xung quanh của phần hình
nón được sơn màu đỏ, ứng với góc
0
90MON =
nên
0
10
90 1
4
360
S
S==
.
Suy ra:
1.
3
d
t
S
S=
Chọn D.
Bài toán 4. Một thợ thủ công trang trí 100
chiếc nón lá có hình nón giống nhau như hình vẽ
bên. Biết
25SA =
cm,
20 3AB =
cm và
0
60AIB =
. Ở phần mặt trước của mỗi chiếc nón (từ
A
đến
B
không chứa điểm
I
) có sơn và vẽ hình
trang trí với giá tiền công là 50000 đồng
2
/m
, phần
còn lại của chiếc nón chỉ sơn với giá tiền công là
12000 đồng
2
/m
. Tổng số tiền (làm tròn đến hàng
nghìn) mà người thợ nhận được mỗi đợt trang trí
nón bằng
A.
387000
đồng. B.
257000
đồng. C.
410000
đồng. D.
262000
đồng.
Giải
Đổi
13
25cm m, 20 3cm m
45
SA AB= = = =
.
Do
0
60AIB =
nên
0
2 120 .AOB AIB==
Áp dụng định lí sin trong tam giác OAB ta có:
sin sin
OA AB
OBA AOB
=
.
Từ đó suy ra:
0
21
. (m)
25
3
2sin120
AB AB
R OA= = = =
, với R là bán kính đường tròn đáy.