
98
TẠP CHÍ KHOA HỌC TÀI CHÍNH KẾ TOÁN
GIỚI THIỆU MỘT SỐ KẾT QUẢ CƠ BẢN VỀ LÝ THUYẾT VIABILITY
CHO BAO HÀM THỨC VI PHÂN
INTRODUCTION OF SOME BASIC RESULTS ABOUT VIABILITY THEORY
FOR INCLUDING DIFFERENTIAL MODELS
ThS. Nguyễn Hoàng Trúc - ThS. Trần Thị Vân Anh
Trường Đại học Tài chính - Kế toán
TÓM TẮT
Bài báo giới thiệu một số kết quả cơ bản về lý thuyết viability cho bao hàm thức vi phân nhằm áp
dụng lý thuyết này vào các bài toán trong thực tế.
Từ khóa: Lý thuyết viability, bao hàm thức vi phân.
ABSTRACT
Ngy nhn bi : 23.5.2022
Ngy nhn kt qu phn bin : 28.8.2022
Ngy duyt đăng : 20.9.2022
TẠP CHÍ KHOA HỌC TÀI CHÍNH KẾ TOÁN
GIỚI THIỆU MỘT SỐ KẾT QUẢ CƠ BẢN VỀ LÝ THUYẾT VIABILITY
CHO BAO HÀM THỨC VI PHÂN
ThS. Nguyễn Hoàng Trúc - ThS. Trần Thị Vân Anh
Trường Đại học Tài chính - Kế toán
TÓM TẮT
Bài báo giới thiệu một số kết quả cơ bản về lý thuyết viability cho bao hàm thức vi phân nhằm áp
dụng lý thuyết này vào các bài toán trong thực tế.
Từ khóa: ý thuyết viability, bao hàm thức vi phân.
ABSTRACT
The article introduces some basic results on viability theory for differential equation inclusion
in order to apply this theory to real-life problems.
Keywords: viability theory, including differential equations.
1. Đặt vấn đề
Bao hm thức vi phân l một công cụ có hiu qu cho vic nghiên cứu bi toán điều khiển tối ưu:
chọn lựa các quỹ đạo để tối ưu một tiêu chí cho trước - một hm trên không gian tất c các quỹ đạo.
Điều ny đòi hỏi các yu tố:
- Có người ra quyt định để điều khiển h thống.
- Người ra quyt định phi có hiểu bit sâu rộng v dự đoán tốt về tương lai (bao gồm vic xác
định các tiêu chí tối ưu).
- Quyt định tối ưu được chọn một lần cho tất c các khong thời gian khác nhau.
Các đòi hỏi ny thường không được đáp ứng trong các h thống “vĩ mô” tuân theo lut tin hóa
Darwinnian. Các h thống như th dường như không có mục tiêu cũng như không mong muốn tối ưu
hóa một tiêu chí no đó. Chúng đòi hỏi một yêu cầu tối thiểu gọi l “viability” (vẫn “sống sót” theo
nghĩa thỏa mãn một số rng buộc).
Xét các bao hm thức vi phân
()
() , ()ut F tut∈
(*)
v
()
() () , ()ut Aut F tut∈+
(**)
v quan tâm đn vic tìm các điều kin cần hoặc điều kin cần v đủ để với mỗi
0
uK∈
, các bao
hm thức (*) hoặc (**) có ít nhất một nghim thỏa điều kin đầu
0
(0)uu=
. Ở đây K l một tp con
của không gian Banach X.
Người tiên phong trong vic nghiên cứu bi toán viability l nh toán học Nagumo, khi xét (*) trong
Ngy nhn bi : 23.5.2022
Ngy nhn kt qu phn bin : 28.8.2022
Ngy duyt đăng : 20.9.2022

99
ĐẠI HỌC TÀI CHÍNH - KẾ TOÁN
ĐẠI HỌC TÀI CHÍNH - KẾ TOÁN
trường hợp X l không gian hữu hạn chiều v F l hm đơn trị liên tục. Vic mở rộng các kt qu của
Nagumo từ phương trình vi phân thường sang bao hm thức vi phân được cho bởi [Bebernes-Schuur,
1970]. Cụ thể hơn, Bebernes-Schuur đã chứng minh rằng nu F l hm đa trị nữa liên tục trên, nhn
giá trị lồi, đóng, bị chặn v khác rỗng, trong khi K l tp đóng địa phương thì K sống được (viable)
tương ứng với F nu v chỉ nu
() ()
k
FJξ ∩ ξ ≠∅
(***)
với mỗi ξ ∈ K, với Jk l nón tip xúc của K tại ξ.
Khi X l không gian vô hạn chiều ta có thể dễ dng thu được một mở rộng của [Bebernes-Schuur,
1970] bằng cách gi sử rằng K l compact địa phương v F nhn giá trị lồi compact khác rỗng (xem
[Aubin-Cellina, 1984]). Năm 1997, Clarke, Ledyaev, v Radulescu đã xét trường hợp X l không
gian Hilbert vô hạn chiều v gim gi thit trên tp K từ compact địa phương thnh đóng địa phương
nhưng đồng thời tăng gi thit trên F bằng cách gi sử rằng:
(CH) tồn tại k > 0 sao cho với bất kỳ tp bị chặn D trong X, ta có
α(F(D)) ≤ kα(D),
trong đó α l độ đo phi compact loại Kuratowski. Ta lưu ý rằng điều kin (CH) kéo theo tính chất
compact của F.
Bằng cách gi sử rằng F có giá trị đóng, bị chặn thay vì compact, v K l compact địa phương
Carja v Monterio Marques (2002) đã thu được điều kin cần v đủ cho tính viability của K tương
ứng với F thỏa (***) với khái nim tp tip xúc yu hơn.
2. Lý thuyết Viability
2.1. Bao hàm thức vi phân
Lý thuyt Viability có vai trò quan trọng trong vic phân tích các h động lực không tất định, v
c các h động lực ngẫu nhiên - một thnh phần quan trọng khi nghiên cứu các vấn đề kinh t v môi
trường. Tính không tất định của h động lực được mô hình trong lý thuyt Viability chủ yu thông
qua các bao hm thức vi phân, có thể được xem như các phương trình vi phân có giá trị tp. Vic mô
t h động lực theo cách ny khác với vic sử dụng các phương trình vi phân ngẫu nhiên, vì không
có một phân bố xác suất no trên tp các trạng thái của h thống.
Ta ký hiu x(t) l trạng thái của một h thống tại thời điểm t > 0. Sự tin hóa của h thống có thể
được mô hình hóa bởi bao hm thức vi phân sau:
(1)
()
() ()xt F xt
•
∈
Có thể hiểu bao hm thức ny như sau: Trạng thái của h thống thay đổi theo thời gian với vn
tốc
()
xt
•
l một phần tử của tp
()
()
F xt
, trong đó F l một hm trạng thái. Tính không tất định của
F(x(t)) có thể đn từ bất kỳ nguồn no sau đây:
(i) H thống có thể được điều khiển bởi người ra quyt định. Trong trường hợp ny, chúng ta có
thể vit lại (1) dưới dạng
(2)
()
() (), ()xt f xt ut
•
=
(3)
() ( ())ut U xt∈
trong đó (2) l một phương trình vi phân tham số chuẩn v (3) l hm chọn u(t) thuộc tp trạng thái
tiềm năng, U(x(t)).
(ii) Có thể có sự không tất định của mô hình động lực cơ bn. Ví dụ, có thể có một số đề xuất

100
TẠP CHÍ KHOA HỌC TÀI CHÍNH KẾ TOÁN
TẠP CHÍ KHOA HỌC TÀI CHÍNH KẾ TOÁN
phương trình vi phân
{}
12
, ,...,
j
ff f
mô t sự tin hóa của h thống. Sau đó, một bao hm thức vi
phân có thể được xây dựng cho h thống như:
(4)
{ }
12
( ) ( ( )), ( ( )),..., ( ( ))
j
xt f xt f xt f xt
•
∈
Một bin thể của điều ny l trường hợp không tất định về các mô hình tham số; tức l
(5)
()
() ,xt f x
•
= γ
Trong đó
γ∈Γ
l một vectơ của các tham số được rút ra từ miền xác định của giá trị gi
thuyt.
(iii) H thống có thể thực sự không tất định, tức l không phi chịu sự xác định thường xuyên.
Điều ny có nghĩa l vic phân tích viễn cnh mọi sự tin hóa thỏa mãn (1) đều có kh năng như nhau.
(iv) Sự kt hợp bất kỳ của các điều trên.
Các bao hm thức vi phân cung cấp một sự trừu tượng hóa trên tất c các kh năng ny. Trong khi
gii pháp cho phương trình vi phân l đường đi của các điểm qua không gian h thống, khái nim gii
pháp về bao hm thức vi phân l tp hợp tất c các đường dẫn có thể nằm trong các rng buộc của
trạng thái “ống” v cũng thỏa mãn các rng buộc đầu cuối thông thường (nu thích hợp).
Điều quan trọng cần lưu ý l bất kỳ phương trình vi phân thông thường no cũng có thể được biểu
diễn dưới dạng bao hm thức vi phân có giá trị l một tp hợp chỉ có một thnh phần trong đó. Nói
cách khác, phương trình vi phân có thể được coi l trường hợp đặc bit của các bao hm thức vi phân,
có nghĩa l mặc dù lý thuyt viability được hướng tới các bao hm thức vi phân, các mô hình sử dụng
phương trình vi phân cũng có thể phân tích được.
2.2. Viability
Cho một bao hm thức vi phân F có giá trị trên X, chúng ta nói rằng
0
xKX∈⊂
l kh thi trong
K theo F nu, bắt đầu từ
0
(0)xx=
,
(6)
()
()
() (),
xt K
t
xt F xt
•
∈
∀ ∈Θ∈
trong đó
[]
0,Θ≡ ∞
. Nói cách khác,
0
x
kh thi trong K nu nó có thể sống sót trong K. K được gọi
l tp rng buộc. Nó l tp đóng, đại din cho các rng buộc viability được áp đặt cho h thống phát
triển theo F.
Công thức (6) cho phép chúng ta nói về tính bền vững của một h thống trạng thái riêng lẻ. Để
đi từ điều ny đn vic xem xét các khu vực viability, lý thuyt viability giới thiu chủ yu định lý
viability, thit lp mối quan h giữa bất kỳ tp hợp điểm D kh thi no theo F v hình nón ngẫu nhiên
tại x l quỹ đạo điểm bên trong tâm D của D, bắt đầu từ x. Định lý viability cho bit rằng bất cứ nơi
no các hướng định sẵn trong F(x) v các hướng trong hình nón ngẫu nhiên tại x giao nhau, thì x sẽ
kh thi. Mối quan h ny được định nghĩa chính thức trong [8], ở đây chúng tôi tái tạo định lí trong
[7] (định lí 2.3) thnh định lí 1 dưới đây. Các kt qu cốt lõi của lý thuyt viability không được biểu
thị dưới dạng không gian vectơ, m trong các không gian chung hơn; tuy nhiên, chúng tôi giới hạn
vic nghiên cứu ở đây cho các không gian vectơ để thun tin.
Định lý 1. Giả sử D là một tập đóng trong
n
,
:
nn
FU×→
liên tục, Lipschitz theo biến
đầu tiên; hơn nữa, với mỗi x chúng ta xác định một ánh xạ có giá trị
( ){ }
, ( , ),f xU f xu u U= ∈
,,
được cho là Lipschitz liên tục với giá trị lồi, compact, khác rỗng.
Hai nhn định sau l tương đương:

101
ĐẠI HỌC TÀI CHÍNH - KẾ TOÁN
TẠP CHÍ KHOA HỌC TÀI CHÍNH KẾ TOÁN
phương trình vi phân
{}
, ,...,ff f
mô t sự tin hóa của h thống. Sau đó, một bao hm thức vi
phân có thể được xây dựng cho h thống như:
(4)
{ }
( ) ( ( )), ( ( )),..., ( ( ))xt f xt f xt f xt
•∈
Một bin thể của điều ny l trường hợp không tất định về các mô hình tham số; tức l
(5)
()
() ,xt f x
•= γ
Trong đó
γ∈Γ
l một vectơ của các tham số được rút ra từ miền xác định của giá trị gi
thuyt.
(iii) H thống có thể thực sự không tất định, tức l không phi chịu sự xác định thường xuyên.
Điều ny có nghĩa l vic phân tích viễn cnh mọi sự tin hóa thỏa mãn (1) đều có kh năng như nhau.
(iv) Sự kt hợp bất kỳ của các điều trên.
Các bao hm thức vi phân cung cấp một sự trừu tượng hóa trên tất c các kh năng ny. Trong khi
gii pháp cho phương trình vi phân l đường đi của các điểm qua không gian h thống, khái nim gii
pháp về bao hm thức vi phân l tp hợp tất c các đường dẫn có thể nằm trong các rng buộc của
trạng thái “ống” v cũng thỏa mãn các rng buộc đầu cuối thông thường (nu thích hợp).
Điều quan trọng cần lưu ý l bất kỳ phương trình vi phân thông thường no cũng có thể được biểu
diễn dưới dạng bao hm thức vi phân có giá trị l một tp hợp chỉ có một thnh phần trong đó. Nói
cách khác, phương trình vi phân có thể được coi l trường hợp đặc bit của các bao hm thức vi phân,
có nghĩa l mặc dù lý thuyt viability được hướng tới các bao hm thức vi phân, các mô hình sử dụng
phương trình vi phân cũng có thể phân tích được.
2.2. Viability
Cho một bao hm thức vi phân F có giá trị trên , chúng ta nói rằng
xKX∈⊂
l kh thi trong
K theo F nu, bắt đầu từ
(0) =
,
(6)
()
()
() (),
xt K
t
xt F xt
•
∈
∀ ∈Θ∈
trong đó
[]
0,Θ≡ ∞
. Nói cách khác, kh thi trong K nu nó có thể sống sót trong K. K được gọi
l tp rng buộc. Nó l tp đóng, đại din cho các rng buộc viability được áp đặt cho h thống phát
triển theo F.
Công thức (6) cho phép chúng ta nói về tính bền vững của một h thống trạng thái riêng lẻ. Để
đi từ điều ny đn vic xem xét các khu vực viability, lý thuyt viability giới thiu chủ yu định lý
viability, thit lp mối quan h giữa bất kỳ tp hợp điểm D kh thi no theo F v hình nón ngẫu nhiên
tại l quỹ đạo điểm bên trong tâm D của D, bắt đầu từ . Định lý viability cho bit rằng bất cứ nơi
no các hướng định sẵn trong F( ) v các hướng trong hình nón ngẫu nhiên tại giao nhau, thì sẽ
kh thi. Mối quan h ny được định nghĩa chính thức trong [8], ở đây chúng tôi tái tạo định lí trong
[7] (định lí 2.3) thnh định lí 1 dưới đây. Các kt qu cốt lõi của lý thuyt viability không được biểu
thị dưới dạng không gian vectơ, m trong các không gian chung hơn; tuy nhiên, chúng tôi giới hạn
vic nghiên cứu ở đây cho các không gian vectơ để thun tin.
Định lý 1. Giả sử D là một tập đóng trong
n
,
nn
FU×→
liên tục, Lipschitz theo biến
đầu tiên; hơn nữa, với mỗi x chúng ta xác định một ánh xạ có giá trị
( ){ }
, ( , ),f xU f xu u U= ∈
,,
được cho là Lipschitz liên tục với giá trị lồi, compact, khác rỗng.
Hai nhn định sau l tương đương:
ĐẠI HỌC TÀI CHÍNH - KẾ TOÁN
(a)
(7)
xD∀∈
,
()p NP x∀∈
,
min ( , ), 0
uf xu p
≤
(tương ứng,
min ( , ), 0
u
f xu p ≤
)
(b) Tồn tại
[]
,tT
uU∈
để m
(tương ứng, cho mọi
[]
,tT
uU∈
)
(8) nghim của
()
() (), ()
()
xs f xs us
xt x
•
=
=
hầu khắp nơi với mọi s trong D
Chú ý rằng sự bình đẳng
min ( , ), 0
u
f xu p ≤
trong (7) nghĩa l tồn tại một điều khiển m h
thống có vn tốc
x
•
l “điểm trong” của D. Tương ứng,
max ( , ), 0
u
f xu p ≤
có nghĩa l h thống
có vn tốc
x
•
l “điểm trong” của D cho tất c các điều khiển từ U.
Khi a (hoặc b) đm bo, chúng ta nói rằng D l miền viability (hoặc D l miền bất bin) cho động
lực học F. Điều ny đưa ra khái nim cổ điển về miền viability (hoặc miền bất bin), trái ngược với
các miền viability trong các vấn đề với các mục tiêu, điều ny xác định rằng liu có thể (hoặc cần
thit, trong trường hợp ánh xạ bất bin) đưa ra được h động lực trong F cho một tp trạng thái các
điểm không gian của một số tp hợp trong D được duy trì một cách chắc chắn, nó đủ để cho thấy sự
tồn tại của các quỹ đạo hướng vo trong ranh giới của D.
Sự tồn tại của một miền viability có ý nghĩa khác nhau, tùy thuộc vo bn chất của F:
(I) Đối với một h điều khiển, tồn tại một miền viability trong D chỉ ra một khu vực tồn tại đủ
kiểm soát để duy trì h thống trong D từ bất kì điểm no trong D. Nghĩa l, đối với mỗi phần tử
0
x
trong D, cần tồn lại một hm (tức l một song ánh)
:gX Y→
tại một phần tử
xX∈
v tr về một
điều khiển u sao cho
(9)
()
, ( ()) ( ()) () (), ( ()) ()t gxt U xt xt f xt g xt xt D
•
∀ ∈Θ ∈ ∧ =
∧∈
trong đó x(t) l một nghim của (2), (3) với
0
(0)xx=
.
(II) Đối với các vấn đề liên quan đn tính không chắc chắn của mô hình hoặc h thống động lực
học không tất định, một miền viability cho thấy một khu vực có tiềm năng ổn định hoặc bền vững. Ở
đây, động lực học của F không loại trừ vic ổn định h thống trong D (tức l không bao giờ rời khỏi
D), nhưng chúng có thể không nhất thit đm bo điều đó. Đối với điều ny, một ánh xạ bất bin phi
được tìm kim.
(III) Khi hai khái nim trên nằm xen kẽ trong cùng một bao hm thức vi phân F, sự tồn tại của
miền viability có nghĩa l có đủ quyền kiểm soát để cung cấp cho h thống cơ hội tồn tại trong D,
nhưng điều đó có thể không nhất thit xy ra.
2.3. Hạt nhân viability - miền viability lớn nhất trong tập ràng buộc
Định nghĩa 2. Cho K là một tập đóng trong
n
. Lớp hạt nhân viability cho hệ động lực F, kí hiệu:
()
F
KV
, là miền viability lớn nhất có thể có trong F cũng là tập con của K.
Do đó hạt nhân viability sẽ l tp tất c các điểm kh thi trong K theo F. Thit lp hạt nhân viability
() 0
F
K≠V
gii quyt vấn đề viability. Đó l, những phần tử tốt
() ( )
F
xt K∈V
có thể tách rời khỏi
các
() ( )
F
xt K∉V
. Trong đó F đại din cho một h thống điều khiển, điều ny có ý nghĩa quan trọng
đối với vic hoạch định chính sách, trong đó nó có thể được sử dụng để xây dựng các quy tắc kiểm
soát duy trì tính bền vững của h thống, như sau: Để
W() ()x Ux⊂
l tp các giá trị điều khiển tại
102
TẠP CHÍ KHOA HỌC TÀI CHÍNH KẾ TOÁN
ĐẠI HỌC TÀI CHÍNH - KẾ TOÁN
Thay vo đó, chỉ cần xác định giới hạn của tp K a, một nhim vụ có kh năng đơn gin hơn nhiều,
với điều kin l các giới hạn đó (có thể l quy tắc hoặc phương thức) thường quan sát được. Hơn
nữa, vic bit hạt nhân viability l một gii pháp cho vấn đề viability, lm cho cơ quan qun lý nhn
thức được vị trí của các trạng thái m h thống động có thể tip tục tồn tại, đối với một điều khiển
có độ bền nhất định. Do đó, Viability l một sự khái quát của sự ổn định, hơn l sự tối ưu. Điều ny
l vì hạt nhân l một tp đóng v nó có thể được đặc trưng bởi một độ đo khong cách giữa hai trạng
thái không bao giờ vượt ra ngoi hạt nhân. Vì vy, một khi đã ở trong hạt nhân, các trạng thái không
phân kỳ. Quan trọng hơn đối với cơ quan qun lý, thông tin về hạt nhân l đủ để thực hin thỏa mãn
chính sách, trái ngược với chính sách tối ưu. Ngoi ra, cách tip cn khá thoi mái được ủng hộ bởi
chỉ thị (i.) phần 2.3, cung cấp cho cơ quan qun lý kh năng phấn đấu để đạt được các mục tiêu khác
(ví dụ: chính trị), khi có nhiều hơn một kiểm soát
W()ux∈
. Các mục tiêu ny có thể không được
sử dụng cho đặc t của bộ rng buộc K, chúng khó xác định theo toán học hoặc chúng phát sinh sau
khi hạt nhân viability được thit lp; chúng được coi đơn thuần chỉ l tốt đẹp để có được - tức l,
“muốn” hơn l “cần”.
TÀI LIỆU THAM KHẢO
1. J.-P. Aubin, Viability kernels and capture basins of sets under differential inclusions, SIAM J. Control
Optimization, 40 (2001), 853–881.
2. J.-P. Aubin and A. Cellina, Differential inclusions, Grundlehren der math, Wiss., no. 264, Springer-Verlag,
1984.
3. Jean-Pierre Aubin and Hélène Frankowska, Set-valued analysis, Birkhauser, Boston, 1990.
4. , Set valued numerical analysis for optimal control and differential games, Stochastic and differential
Games: Theory and Numerical Methods, Ann. Internat. Soc. Dynam. Games 4 (1999), 177–274.
5. M. Quincampoix and P. Saint-Pierre, An algorithm for viability kernels in h¨olderian case: Approximation
by discrete dynamical systems, Journal of Mathematical Systems, Estimation and Control 5 (1995), no.
1, 1–13.
6. M. Quincampoix and V. M. Veliov, Viability with a target: Theory and applications, Applications of
Mathematical Engineering, Cheshankov B. and Todorov M, eds, Heron Press, Sofia, pp.
7. H. A. Simon, A behavioral model of rational choice, Quarterly Journal of Economics 69 (1955), 99–118.
8. M. Quincampoix and V. M. Veliov, Viability with a target: Theory and applications, Applications of
Mathematical Engineering, Cheshankov B. and Todorov M., eds., Heron Press, Sofia, pp. 47 (1998), 47-58.
TẠP CHÍ KHOA HỌC TÀI CHÍNH KẾ TOÁN
mọi
()
F
xK∈V
. Vì
()
F
KK⊂V
l hạt nhân viability, nên phi tồn tại ít nhất một điều khiển trong
W( ( ))xt
giữ cho sự tin hóa của h thống bên trong
()
F
KV
; chúng tôi sẽ biểu thị bộ sưu tp các
điều khiển
W()x
V
ny. Từ đó, quy tắc chính sách chung sau đây có thể được xây dựng:
(10)
()
F
xK∀∈V
ứng với
W()ux∈
V
Trong đó
{
W() : (,)x u U f xu≡∈
V
thuộc hình nón tại
}
x
Vì vy, hướng của
(,)f xu
l hướng tip tuyn hoặc hướng vo
()
F
KV
tại x.
Quy tắc chung ny có thể được tách thnh hai chỉ thị cho một vấn đề viability nhất định:
(i) phần trong của hạt nhân viability
()\ ()
FF
K fr KVV
, có thể sử dụng cho bất kỳ điều khiển
no từ
W( )x
;
(ii) trên biên
()
F
fr KV
của hạt nhân, phi tuân theo một công cụ đặc bit hoặc một đường dẫn cụ thể.
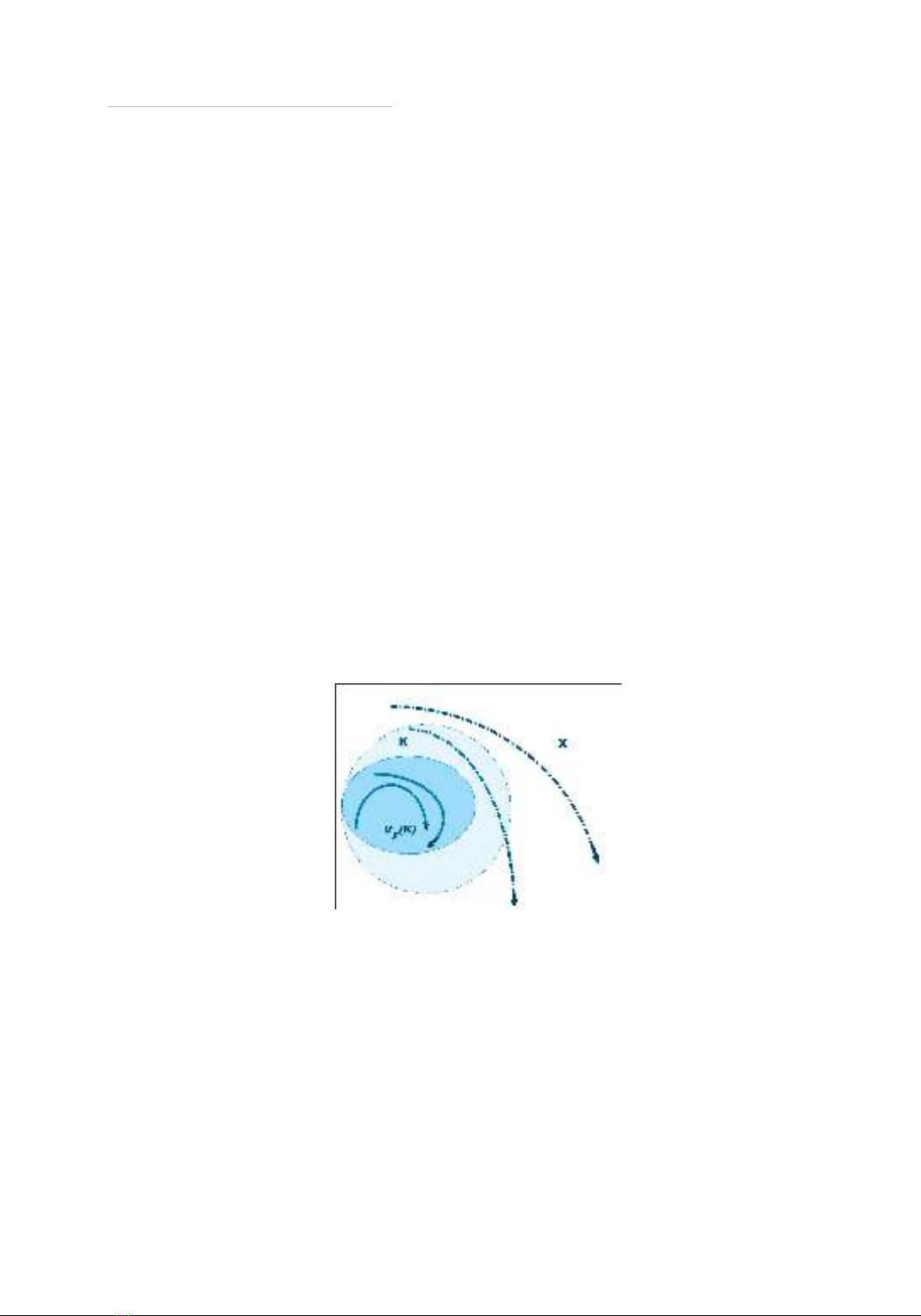
Hình 1 cung cấp một gii thích hình học của các khái nim được trình by ở trên cho một vấn đề
điều khiển với động lực xác định. Tp rng buộc trạng thái K được biểu thị bằng hình tròn mu vng
có trong không gian trạng thái (trong đó X biểu thị không gian trạng thái; ở đây,
2
x≡
). Hạt nhân
viability cho tp rng buộc K, các điều khiển từ tp U(x) v h thống động lực học F, l đường viền
tối mu nâu. Các đường liền nét tượng trưng cho sự tin hóa của h thống. Nu một sự tin hóa bắt
đầu bên trong hạt nhân viability
()
F
KV
thì chúng ta có đủ các điều khiển để giữ nó trong tp rng
buộc K khi
t∈Θ
. Sự tin hóa của h thống được đại din bởi các quỹ đạo bắt đầu bên trong hạt nhân
(đường liền nét) kh thi trong K tức l, chúng vẫn ở K. Đây không phi l thuộc tính của các quỹ
đạo khác (đường chấm chấm) bắt đầu bên ngoi hạt nhân. Chúng rời khỏi K trong thời gian vô hạn.
Hình 1. Các quỹ đạo khả thi và không khả thi.
2.4. Viability và tối ưu.
Không thể quá nhấn mạnh rằng nghiên cứu lý thuyt viability l một hướng nghiên cứu khác với
vic nghiên cứu lý thuyt tối ưu.
Một điểm khác bit quan trọng giữa hai cách tip cn ny l nghim trong các vấn đề của lý thuyt
viability xác định rõ rng tp hợp các trạng thái chấp nhn được trong K, trong khi phương pháp tối
ưu hóa, các rng buộc xác định trong K thường ẩn trong hm mất mát. Một kt qu dễ nhn thấy về
vấn đề ny l các vấn đề được mô hình hóa bằng cách sử dụng lý thuyt viability không cần xác định
các hm tin ích hoặc mất mát để xây dựng các quy tắc chính sách v do đó không cần phi hiu chỉnh
các chức năng đó, điều ny sẽ dẫn đn vic đánh giá chủ quan về những hạn ch no quan trọng hơn.






![Định lý hình học nổi tiếng: Tổng hợp [năm hiện tại]](https://cdn.tailieu.vn/images/document/thumbnail/2022/20221107/phuonghung205/135x160/6531667812167.jpg)


















![Quyển ghi Xác suất và Thống kê [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251030/anh26012006/135x160/68811762164229.jpg)
