MÔ HÌNH H I QUY Ồ
HAI BI N (ti p theo)Ế ế
Ch ng 2 ươ
I. Ki M Đ NH MÔ HÌNH H I QUYỂ Ị Ồ
1. Các đ i l ng ng u nhiênạ ượ ẫ
Gi s ả ử Ui ~ N(0,σ2)
Theo gi thi t c a ph ng pháp OLS, Uả ế ủ ươ i là đ i l ng ng u ạ ượ ẫ
nhiên có giá tr trung bình b ng 0 và ph ng sai không thay ị ằ ươ
đ i ổ
Khi đó σ2 đ c g i là ph ng sai c a t ng th , r t khó tính ượ ọ ươ ủ ổ ể ấ
đ c nên th ng đ c c l ng b ng ph ng sai m u ượ ườ ượ ướ ượ ằ ươ ẫ
22
)
ˆ
(
2
ˆ
22
2
−
=
−
−
=
−
=∑∑
n
RSS
n
YY
n
e
iii
σ
a. Đ i l ng ng u nhiên Uạ ượ ẫ
i
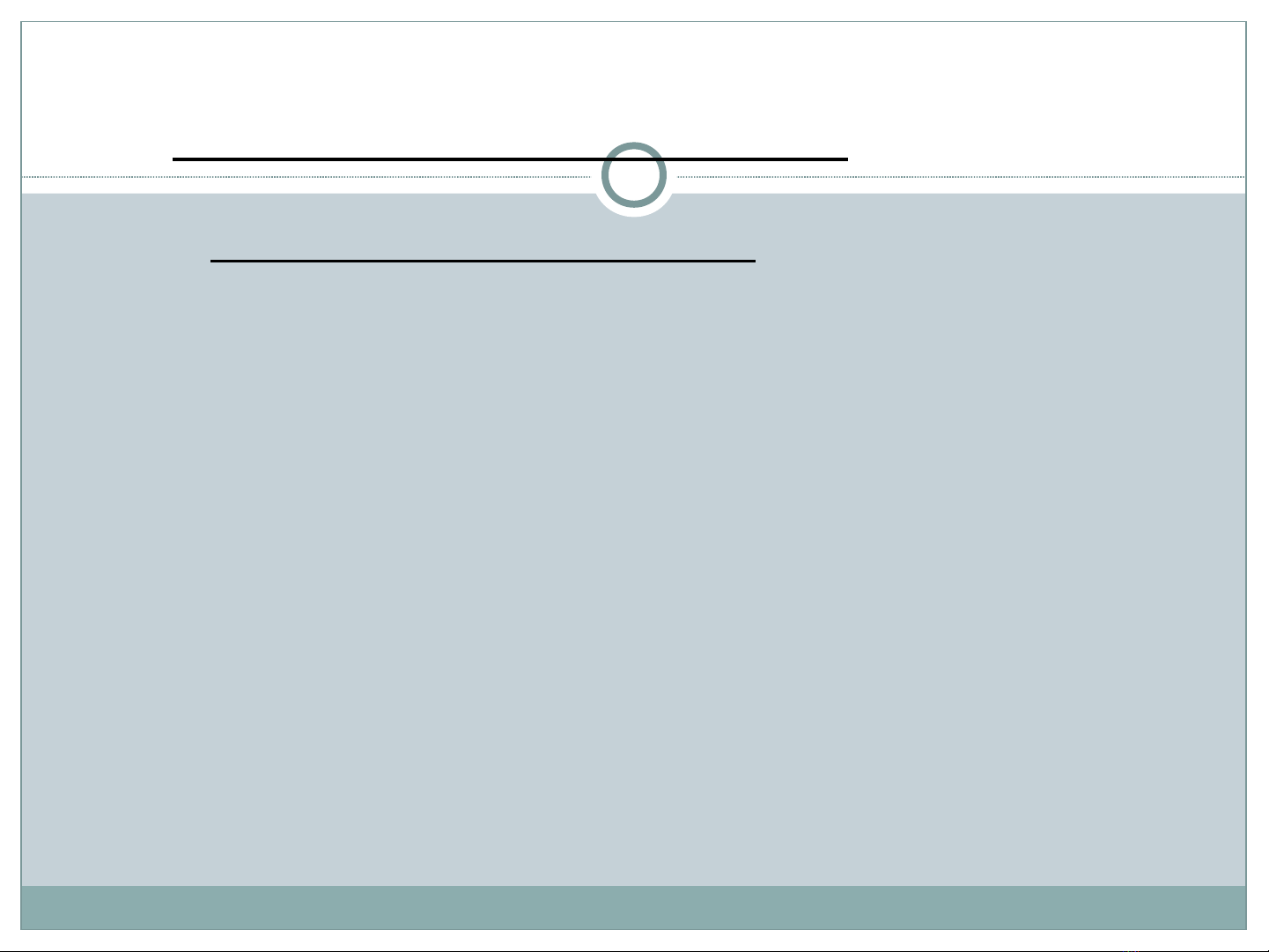
Vì Ui ~ N(0,σ2)
Nên Yi ~ N(β1+β2Xi,σ2)
iii
UXY ++=
21
ββ
Ta có
I. Ki M Đ NH MÔ HÌNH H I QUYỂ Ị Ồ
1. Các đ i l ng ng u nhiênạ ượ ẫ
a. Đ i l ng ng u nhiên Uạ ượ ẫ
i
I. Ki M Đ NH MÔ HÌNH H I QUYỂ Ị Ồ
1. Các đ i l ng ng u nhiênạ ượ ẫ
a
21
ˆ
,
ˆ
ββ
M i m u thì ch tính đ c duy nh t m t ỗ ẫ ỉ ượ ấ ộ
21
ˆ
,
ˆ
ββ
a. Đ i l ng ng u nhiênạ ượ ẫ
21
ˆ
,
ˆ
ββ
Nh ng t ng th có r t nhi u m u và cách ch n m u là ng u nhiên ư ổ ể ấ ề ẫ ọ ẫ ẫ
nên cũng ng u nhiênẫ
21 ˆ
,
ˆ
ββ
),(
ˆ
2
ˆ
11
1
β
σββ
N
≈
),(
ˆ
2
ˆ
22
2
β
σββ
N≈
Trong đó
2
ˆ
1
β
σ
là ph ng sai ươ
c a ủ
1
ˆ
β
2
ˆ
2
β
σ
là ph ng sai ươ
c a ủ
2
ˆ
β
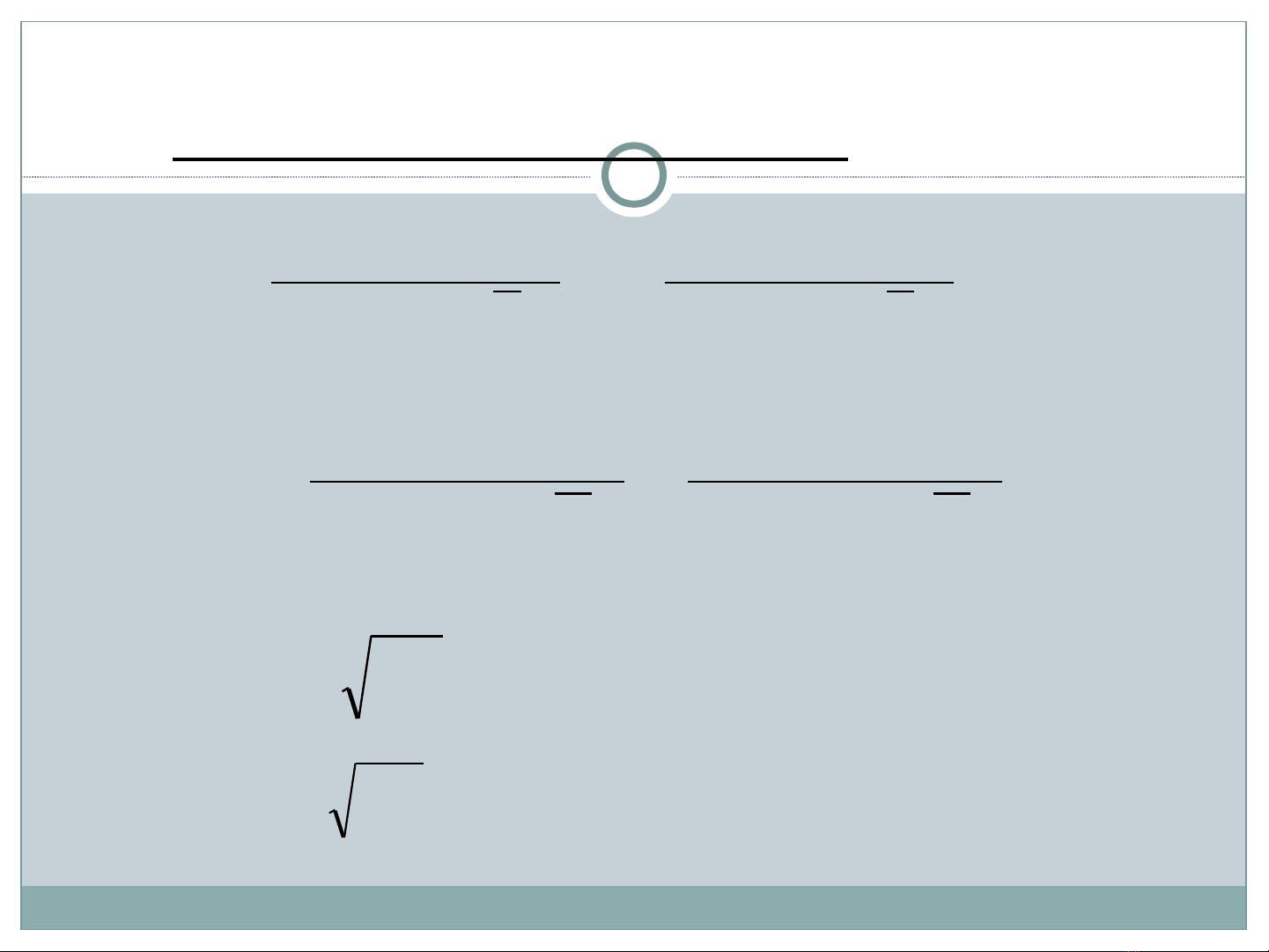
I. Ki M Đ NH MÔ HÌNH H I QUYỂ Ị Ồ
1. Các đ i l ng ng u nhiênạ ượ ẫ
V i ớ
2
22
2
2
22
2
2
ˆ
ˆ
)()(
1
σσσ
β
∑∑
∑∑
−
≈
−
=XnXn
X
XnXn
X
i
i
i
i
∑∑
−
≈
−
=
22
2
22
2
2
ˆ
ˆ
1
XnXXnX
ii
σσ
σ
β
2
ˆ
1
1
)
ˆ
(
β
σβ
=se
đ l ch chu n ộ ệ ẩ
c a ủ
1
ˆ
β
2
ˆ
2
2
)
ˆ
(
β
σβ
=se
đ l ch chu n ộ ệ ẩ
c a ủ
2
ˆ
β