
PHƯƠNG TRÌNH CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI
A. BÀI GIẢNG
1. NHẮC LẠI VỀ GIÁ TRỊ TUYỆT ĐỐI
Với số a, ta có:
nÕu 0
nÕu 0
a a
aa a
Tương tự như vậy, với đa thức ta cũng có:
( ) nÕu ( ) 0
( )
( ) nÕu ( ) 0
f x f x
f x f x f x
Ví dụ 1. Rút gọn các biểu thức:
. 3 7 4 0
a C x x khi x
. 5 4 6 6
b D x x khi x
Giải
a. Với
0
x
thì
3 0
x
nên ta nhận được:
3 7 4 4 4
C x x x
b. Với
6
x
thì
6 0
x
nên ta nhận được:
5 4 6 11 5
D x x x
.
2. GIẢI PHƯƠNG TRÌNH CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI
Trong phạm vi kiến thức lớp 8 chúng ta sẽ chỉ quan tâm tới ba dạng phương trình chứa dấu giá trị tuyệt
đối, bao gồm:
Dạng 1: Phương trình:
( )
f x k
, với k là hằng số không âm.
Dạng 2: Phương trình:
( ) ( )
f x g x
Dạng 3: Phương trình:
( ) ( )
f x g x
Ví dụ 2. Giải các phương trình:
. 5 3 1
a x x
. 5 2 21
b x x
Giải
a. Ta có thể trình bày theo các cách sau:
Cách 1: Ta có:
5 5
5
5 5
x khi x
xx khi x
.
Xét hai trường hợp:

Trường hợp 1: Nếu
5
x
phương trình có dạng:
5 3 1 3 5 1 2 4 2
x x x x x x
, thỏa mãn điều kiện.
Trường hợp 2: Nếu
5
x
phương trình có dạng:
3
5 3 1 3 5 1 4 6
2
x x x x x x
, không thỏa mãn điều kiện.
Vậy, phương trình có nghiệm
2
x
.
Cách 2: Với điều kiện:
1
3 1 0
3
x x
Khi đó, phương trình được biến đổi:
2
5 3 1 2 4 3
5 (3 1) 4
(lo¹ )
2
i
6
x
x x x
x x x x
Vậy, phương trình có nghiệm
2
x
.
b. Viết lại phương trình dưới dạng:
5 2 21
x x
Ta có thể trình bày theo các cách sau:
Cách 1: Ta có:
5x 0
5
5 0
khi x
xx khi x
.
Xét hai trường hợp:
Trường hợp 1: Nếu
0
x
phương trình có dạng:
5 2 21 3 21 7
x x x x , thỏa mãn điều kiện.
Trường hợp 2: Nếu
0
x
phương trình có dạng:
5 2 21 7 21 3
x x x x
, thỏa mãn điều kiện.
Vậy, phương trình có nghiệm
7
x
và
3
x
.
Cách 2: Với điều kiện:
21
2 21 0
2
x x
(*)
Khi đó, phương trình được biến đổi:
5 2 21 3 21 7
5 (2 21) 7 21 3
x x x x
x x x x
, thỏa mãn (*)
Vậy, phương trình có nghiệm
7
x
và
3
x
.
B. PHƯƠNG PHÁP GIẢI TOÁN
Dạng toán 1: PHÁ DẤU TRỊ TUYỆT ĐỐI
Ví dụ 1. Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức:

. 3 2 5
a A x x
trong hai trường hợp
0
x
và
0
x
.
. 4 2 12
b B x x
trong hai trường hợp
0
x
và
0
x
.
. 4 2 12
c C x x
khi
5
x
.
. 3 2 5
d D x x
Giải
a. Ta có:
5 0
5
5 0
x khi x
xx khi x
Do đó:
3 2 5 0 8 2 0
3 2 5 0 2 2 0
x x khi x x khi x
Ax x khi x x khi x
b. Ta có:
4 0
4
4 0
x khi x
xx khi x
Do đó:
4 2 12 0 6 12 0
4 2 12 0 2 12 0
x x khi x x khi x
Bx x khi x x khi x
c. Ta có:
4 4 5
x x khi x
Do đó:
4 2 12 8
C x x x
d. Ta có:
5 5
5
5 5
x khi x
xx khi x
Do đó:
3 2 5 5 4 7 5
3 2 5 5 2 3 5
x x khi x x khi x
Dx x khi x x khi x
Ví dụ 2. Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức:
. 2 3 2 2
a A x x khi x
. 3 3 2 8 3
b B x x x khi x
Giải
a. Với giả thiết
2
x
, ta suy ra:
2 0 2 2
x x x
Do đó, A được viết lại:
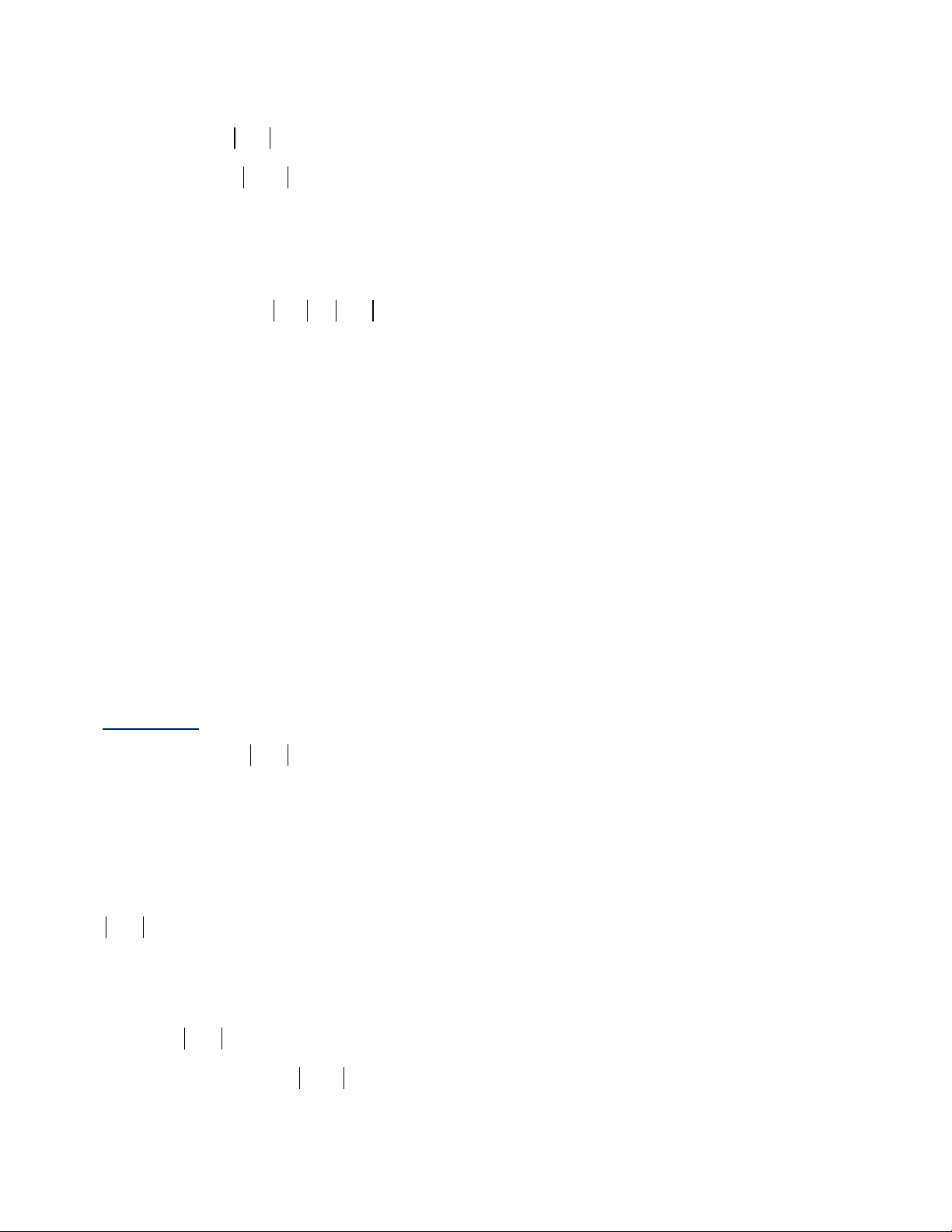
2 3 2 4 4
A x x x
b. Với giả thiết
3
x
, ta suy ra:
3 0 3 3
x x x
3 2 0 3 2 (3 2 )
x x x
Do đó, B được viết lại:
3 (3 2 ) 8 3 3 2 8 4 2
B x x x x x x x
Ví dụ 3. Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức:
1 2 2 3
C x x
Hướng dẫn: Tạo các khoảng chia tương ứng để xét dấu.
Giải
Nhận xét rằng:
1 0 1
x x
2 0 2
x x
Do đó, để bỏ được dấu giá trị tuyệt đối của C ta cần xét các trường hợp:
Trường hợp 1: Nếu
2
x
, ta được:
( 1) 2( 2) 3 3
C x x x
Trường hợp 2: Nếu
2 1
x
, ta được:
( 1) 2( 2) 3 8
C x x x
Trường hợp 3: Nếu
1
x
, ta được:
( 1) 2( 2) 3 3 6
C x x x
Dạng toán 2: GIẢI PHƯƠNG TRÌNH DẠNG
( )
f x k
, với k là hằng số không âm.
Phương pháp
Thực hiện theo các bước:
Bước 1: Đặt điều kiện để f(x) xác định (nếu cần).
Bước 2: Khi đó:
( )
( ) ( )
f x k
f x k
f x k
=> nghiệm x.
Bước 3: Kiểm tra điều kiện, từ đó đưa ra kết luận nghiệm cho phương trình:
Chú ý: Hệ hoặc trong bước 2 có được là nhờ kiến thức giải phương trình tích (chương III), cụ thể:
2 2
( ) ( ) ( ) ( ) 0
f x k f x k f x k f x k
Ví dụ 1. Giải phương trình
2 3 1
x
.
Giải
Biến đổi tương đương phương trình:

2 3 1 2 1 3 2
2 3 1
2 3 1 2 1 3 1
x x x
xx x x
.
Vậy, phương trình có hai nghiệm
2
x
và
1
x
.
Ví dụ 2. Giải phương trình:
2
1
2
x
x
.
Giải
Điều kiện xác định của phương trình là
2
x
.
Ta có thể lựa chọn một trong hai cách trình bày sau:
Cách 1: Biến đổi tương đương phương trình:
212 2
22
1 0
2 2 ( 2)
21
2
x
x x
xxx
x x x
x
x
Vậy, phương trình có nghiệm
0
x
.
Cách 2: Biến đổi tương đương phương trình:
2 2
2
1 2 2 0
2 ( 2)
2
x x
xx x x
x x
x
Vậy, phương trình có nghiệm
0
x
.
Dạng toán 3: GIẢI PHƯƠNG TRÌNH DẠNG
( ) ( )
f x g x
Phương pháp
Thực hiện theo các bước:
Bước 1: Đặt điều kiện để f(x) và g(x) xác định (nếu cần).
Bước 2: Khi đó:
( ) ( )
( ) ( )
( ) ( )
f x g x
f x g x
f x g x
=> nghiệm x.
Bước 3: Kiểm tra điều kiện, từ đó đưa ra kết luận nghiệm cho phương trình.
Ví dụ 1: Giải các phương trình sau:
. 2 3 3
a x x
22
. 0
1
x x
b x
x
Giải
a. Biến đổi tương đương phương trình:
2 3 3 2 3 3 6
2 3 3
2 3 ( 3) 2 3 3 0
x x x x x
x x x x x x x
Vậy, phương trình có hai nghiệm
6
x
và
0
x
.


























