1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊNĐỀTÍNHDIỆNTÍCHTAMGIÁC,DIỆNTÍCHTỨGIÁC
NHỜSỬDỤNGCÁCTỈSỐLƯỢNGGIÁC
A. KIẾNTHỨCCẦNNHỚ
.Tađãbiếtcáchtínhdiệntíchtamgiáctheomộtcôngthứcrấtquenthuộclà
1,
2
Sah
trongđóalàđộdàimột
cạnhcủatamgiác,hlàchiềucaoứngvớicạnhđó.
.Bâygiờtavậndụngcáctỉsốlượnggiác,cáchệthứcvềcạnhvàgóctrongtamgiácvuôngđểxâydựngthêmcác
côngthứctínhdiệntíchtamgiác,tứgiác.
B. BÀITẬPMINHHỌA
Vídụ1.Chứngminhrằngdiệntíchmộttamgiácbằngnửatíchhaicạnhnhânvớisincủagóc
nhọntạobởicácđườngthẳngchứahaicạnhấy.
Giải
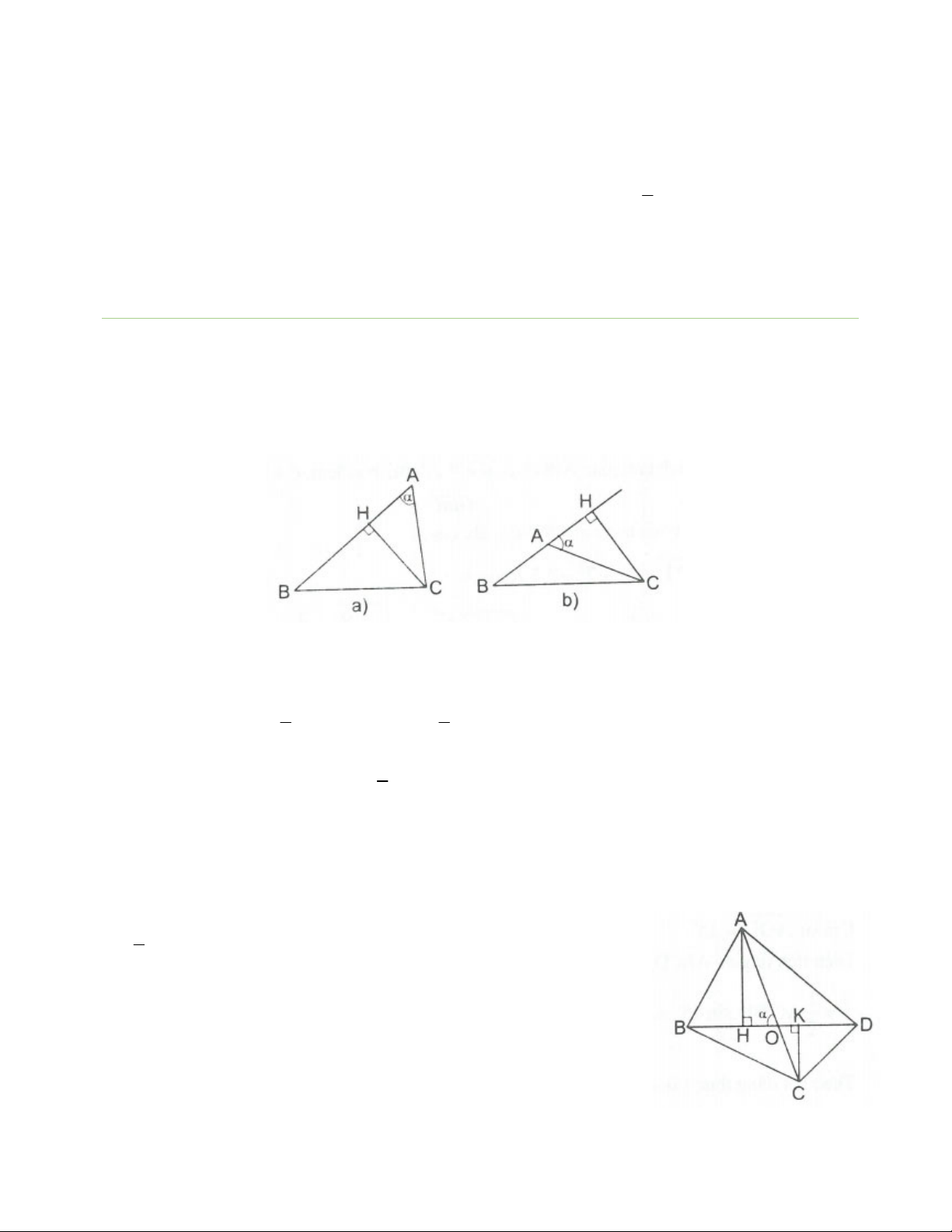
Gọi
làgócnhọntạobởihaiđườngthẳngchứahaicạnhAB,ACcủatamgiácABC.Vẽđường
caoCH.Xét
ACH
vuôngtạiHcó
.sinCH AC
Diệntích
ABC
là
1..
2
SABCH
Dodó
1..sin.
2
SABAC
Lưuý:Nếu
0
90 ,
tacóngay
1.
2
SABAC
Nhưvậy
0
90 1,sin điềunàysẽhọcởcáclớptrên.
Vídụ2.TứgiácABCDcó
, ,AC m BD n
gócnhọntạobởihaiđườngchéobằng
.
Chứngminhrằngdiệntíchcủatứgiácnàyđượctínhtheocôngthức
1sin .
2
Smn
Giải
GọiOlàgiaođiểmcủaACvàBD.Giảsử
.BOC
Vẽ
, .AH BD CK BD
Tacó
sin ;AH OA
sinCK OC
và
.OA OC AC

2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Diệntíchtứgiác
ABCD
là:
11
..
22
11
()(OAsinsin)
22
111
sin ( ) . sin sin
222
ABD CBD
SS S BDAH BDCK
BD AH CK BD OC
BD OA OC AC BD mn
Lưuý:
•Nếu
AC BD
tacóngay
11
.
22
AC BD mSn
•Phươngpháptínhdiệntíchcủatứgiáctrongvídụnàylàchiatứgiácthànhhaitamgiác
khôngcóđiểmtrongchung,rồitínhdiệntíchcủatừngtamgiác.
Vídụ3.ChotamgiácnhọnABC.GọiđộdàicáccạnhBC,CA,ABlầnlượtlàa,b,c.Tínhdiện
tíchtamgiácABCbiết
42 , 5 , 7 .acmbcmccm
Giải
Theođịnhlícôsintacó:
222
2cos.abc bc A
Dođó
222
4 2 5 7 2.5.7.cos A
Suyra
2
394
cos sin 1 cos 1
5255
AA A
VậydiệntíchtamgiácABClà:
2
114
sin .5.7. 14
225
SbcA cm
Nhậnxét:Trongcáchgiảitrêntađãtìm
cos A
rồisuyra
sin .A
Tacũngcóthểvậndụngđịnhlí
côsinđểtìm
cos B
rồisuyra
sin B
(hoặctìm
cosC
rồisuyra
sin )C
Vídụ4.TứgiácABCDcó
12 .AC BD cm
Gócnhọngiữahaiđườngchéolà
45 .
Tínhdiệntích
lớnnhấtcủatứgiácđó.
Giải
GọiOlàgiaođiểmcủaACvàBD.
Giảsử
45 .AOD
DiệntíchtứgiácABCDlà:
1122
..sin45 .. ..
2224
S ACBD ACBD ACBD
TheobấtđẳngthứcCô‐si,tacó:
2
.2
AC BD
AC BD

3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Dođó
2
22
22
.6 9 2
42 4
AC BD
Scm
Vậy
2
max 9 2Scm
khi
6.AC BD cm
Vídụ5.Chotamgiác
, 60 .ABC A
VẽđườngphângiácAD.
Chứngminhrằng:
11 3
AB AC AD
Giải
Tacó
0
111
..sin30 ..
222
ABD
SABAD ABAD
111
.. sin30 ...
222
ACD
S ACAD ACAD
113
..sin60 ..
222
ABC
S ABAC ABAC
Mặtkhác
ABD ACD ABC
SSS
nên
11111 3
.. .. ..
22222 2
AB AD AC AD AB AC
Dođó
.3AD AB AC AB AC
Suyra
AB AC 3 1 1 3
hay .
AB.AC AD AB AC AD
Nhậnxét:PhưongphápgiảitrongvídụnàydựatrênquanhệtổngdiệntíchcáctamgiácABD
vàtamgiácACDbằngdiệntíchtamgiácABC.
Vídụ6.TamgiácABCcómỗicạnhđềunhỏhơn4cm.Chứngminhrằngtamgiácnàycódiện
tíchnhỏhơn
2
7cm
Giải
Giảsử
,ABC
khiđó
60Avà
3
sin 2
A
DiệntíchtamgiácABClà:
2
113
. .sin .4.4. 4 3 6,92... 7 .
222
SABACA cm
Nhậnxét:DovaitròcácgócA,B,CcủatamgiácABClànhưnhaunêntacóthểgiảsử
,ABC
từđósuyra
60 ,A
dẫntới
3
sin 2
A

4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
C. BÀITẬPTỰLUYỆN
•Tínhdiệntích
Bài1.Chứngminhrằngdiệntíchcùahìnhbìnhhànhbằngdiệntíchcủahaicạnhkềnhânvới
sincủagócnhọntạobởihaiđườngthẳngchứahaicạnhấy.
Bài2.Chohìnhchữnhật
, ABCD AC a
và
045.BAC
Chứngminhrằngdiệntích
củahìnhchữnhậtABCDlà
2
1sin 2
2
Sa
Bài3.ChogócnhọnxOy.TrêntiaOxlấyđiểmAvàC,trêntiaOylấyđiểmBvàDsaocho
,.
OA OB
mn
OC OD
Chứngminhrằng
.
AOB
COD
Smn
S
Bài4.TamgiácnhọnABCcó
, , .BC a CA b AB c
GọidiệntíchtamgiácABClàS.Chứng
minhrằng
222
.
4cot
bca
SA
Ápdụngvới
39, 40, 41abc
và
45 .ATínhS.
Bài5.ChogócxOycósốđobằng
45 .
TrênhaicạnhOxvàOylầnlượtlấyhaiđiểmAvàBsao
cho
8.OA OB cm
TínhdiệntíchlớnnhấtcủatamgiácAOB.
Bài6.ChotamgiácnhọnABC.TrêncáccạnhAB,BC,CAlầnlượtlấycácđiểmM,N,Psaocho
1,
4
AM AB
11
, .
32
BN BC CP CA
ChứngminhrằngdiệntíchtamgiácMNPnhỏhơn
1
3
diện
tíchtamgiácABC.
Bài7.Chođoạnthẳng
5.AB cm
LấyđiểmOnằmgiữaAvàBsaocho
2.OA cm
Trênmộtnửa
mặtphẳngbờABvẽcáctiaAx,BycùngvuônggócvớiAB.MộtgócvuôngđỉnhOcóhaicạnh
cắtcáctiaAx,BylầnlượttạiDvàE.TínhdiệntíchnhỏnhấtcủatamgiácDOE.
Bài8.ChohìnhbìnhhànhABCD,gócBnhọn.GọiHvàKlầnlượtlàhìnhchiếucủaAtrêncác
đườngthẳngDCvàBC.
a)Chứngminhrằng
,KAH ABC
từđósuyra
.sin ;KH AC B
b)Cho
, AB a BC b
và
60 .BTínhdiệntích
AHK
vàtứgiácAKCH.
•Chứngminhcáchệthức
Bài9.Chotamgiác
(),60.ABC AB AC A
ĐườngphângiácngoàitạiđỉnhAcắtđườngthẳng
BCtạiN.Chứngminhrằng:
11 1
AB AC AN
Bài10.ChotamgiácABCvuôngtại
.AAB AC
Cácđườngphângiáctrongvàngoàitạiđỉnh
AcủatamgiáccắtđườngthẳngBCtạiMvàN.Chứngminhrằng:
a)
11 2
AM AN AB
b)
11 2
AM AN AC

5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài11.Chotamgiác
0
,90.ABC A
VẽđườngphângiácAD.Chứngminhrằng:
2cos
11 2
AB AC AD
Bài12.ChogócxOycósốđobằng
30 .
TrêntiaphângiáccủagócđólấyđiểmAsaocho
OA a
.
QuaAvẽmộtđườngthẳngcắtOxvàOytheothứtựtạiBvàC.
Tínhgiátrịcủatổng
11
OB OC
Bài13.ChohìnhbìnhhànhABCD,gócnhọngiữahaiđườngchéobằnggócnhọncủahìnhbình
hành.Chứngminhrằngđộdàihaiđườngchéotỉlệvớiđộdàihaicạnhkềcủahìnhbìnhhành.
•Tínhsốđogóc.Tínhđộdài
Bài14.TamgiácnhọnABCcó
4, 6 ; 5,5AB cm BC cm
vàcódiệntíchlà
2
9, 69 .cm Tínhsốđo
gócB(làmtrònđếnđộ).
Bài15.Chohìnhbìnhhành
, 90 .ABCD B
Biết
4, 3AB cm BC cm
vàdiệntíchcủahìnhbình
hànhlà
2
63 .cm Tínhsốđocácgóccủahìnhbìnhhành.
Bài16.ChotamgiácABCcódiệntích
2
50 , 90 .ScmA
TrênhaicạnhABvàAClầnlượt
lấycácđiểmDvàEsaocho
ADE
nhọn,códiệntíchlà
1
1.
2
SS
Chứngminhrằng
10 tan 2
DE cm
Bài17.ChotamgiácABC,đườngphângiácAD.Biết
4, 7 , 5,3
AB cm AC cm
và
72 .ATính
độdàiAD(làmtrònđếnhàngphầnmười).
Bài18.Chotamgiác
, 6 , 12 , 120 .ABC AB cm AC cm A
VẽđườngphângiácAD.Tínhđộdài
AD.
Bài19.Chotamgiác
, 5 , 7 , 8 .
ABC AB cm BC cm CA cm
VẽđườngphângiácAD.Tínhđộdài
AD.
Bài20.ChotamgiácABC,đườngphângiácAD.Biết
11 1
,
AB AC AD
tínhsốđogócBAC.
HƯỚNGDẪN
Bài1.Xéthìnhbìnhhành
, 90 .ABCD D
VẽđườngcaoAH.
XéttamgiácADHvuôngtạiH,tacó:
.sinAH AD


























