Đề án "Dùng phương pháp dãy số thời gian để phân tích sự biến động tổng doanh thu của công ty TNHH THIẾT BỊ GIẶT LÀ CÔNG NGHIỆP và dự báo năm 2004"

Đề án Lý thuyết thống kê

LỜI MỞ ĐẦU

Trong xu thế hội nhập và toàn cầu hoá nền kinh tế ngày càng phát triển và

mở rộng. Sự thông thương giao dịch giữa các nước cũng như các vùng trong một

quốc gia ngày càng được mở rộng. Điều đó sẽ tạo ra nhiều cơ hội cho phát triển

kinh tế, nhưng đồng thời cũng tạo ra nhiều thách thức mới cho các nước đang phát

triển. Muốn phát triển kinh tế phải mở rộng giao lưu buôn bán với nước ngoài cũng

như trong nước, nắm bắt được những cơ hội, phát huy lợi thế, tìm ra hướng đi phù

hợp và hạn chế được những khó khăn do xu thế toàn cầu hoá tạo ra.

Việt Nam là một nước đang phát triển, với dân số hơn 70 triệu. Thu nhập

của người dân ngày càng cao. Tạo ra mức sống ngày một khấm khá hơn, vì thế nhu

cầu về sinh hoạt, chăm sóc, bảo hiểm y tế càng phát triển mạnh. Điều đó dẫn đến

nhu cầu tiêu thụ về các mặt hàng phục vụ đời sống như máy giặt, máy sấy… được

dùng trong sinh hoạt gia đình ngày càng cao.

Đầu tư vào ngành buôn bán các thiết bị phục vụ gia đình sẽ tạo ra những cơ

hội thách thức lớn đối với các doanh nghiệp. Trong những năm gần đây sự đóng

góp của các doanh nghiệp tư nhân vào sự phát triển kinh tế, đã chiếm một tỷ trọng

lớn. Đứng trước những đóng góp của các doanh nghiệp tư nhân đối với phát triển

nền kinh tế quốc dân. Cho nên em chọn đề tài: "Dùng phương pháp dãy số thời

gian để phân tích sự biến động tổng doanh thu của công ty TNHH THIẾT BỊ

GIẶT LÀ CÔNG NGHIỆP và dự báo năm 2004"

Đề án không tránh khỏi những thiếu sót mong thầy cô và các bạn sinh viên

đóng góp thêm. Đề án được hoàn thành dưới sự giúp đỡ của Ths. Trần Phương

Lan.

Em xin chân thành cảm ơn !

Sinh viên

2

Nguyễn Văn Thiệu

Nguyễn Văn Thiệu

Đề án Lý thuyết thống kê

3

Nguyễn Văn Thiệu

Đề án Lý thuyết thống kê

CHƯƠNG 1

KHÁI NIỆM VỀ DÃY SỐ THỜI GIAN

1- Khái niệm về dãy số thời gian

Dãy số thời gian là dãy các trị số của chỉ tiêu thống kê được xắp xếp theo chỉ

tiêu thống kê.

Mặt lượng của hiện tượng thường xuyên biến động qua thời gian.trong thống kê,để

nghiên cứu sự biến động này, người ta thường dựa vàodãy sồ thời gian.

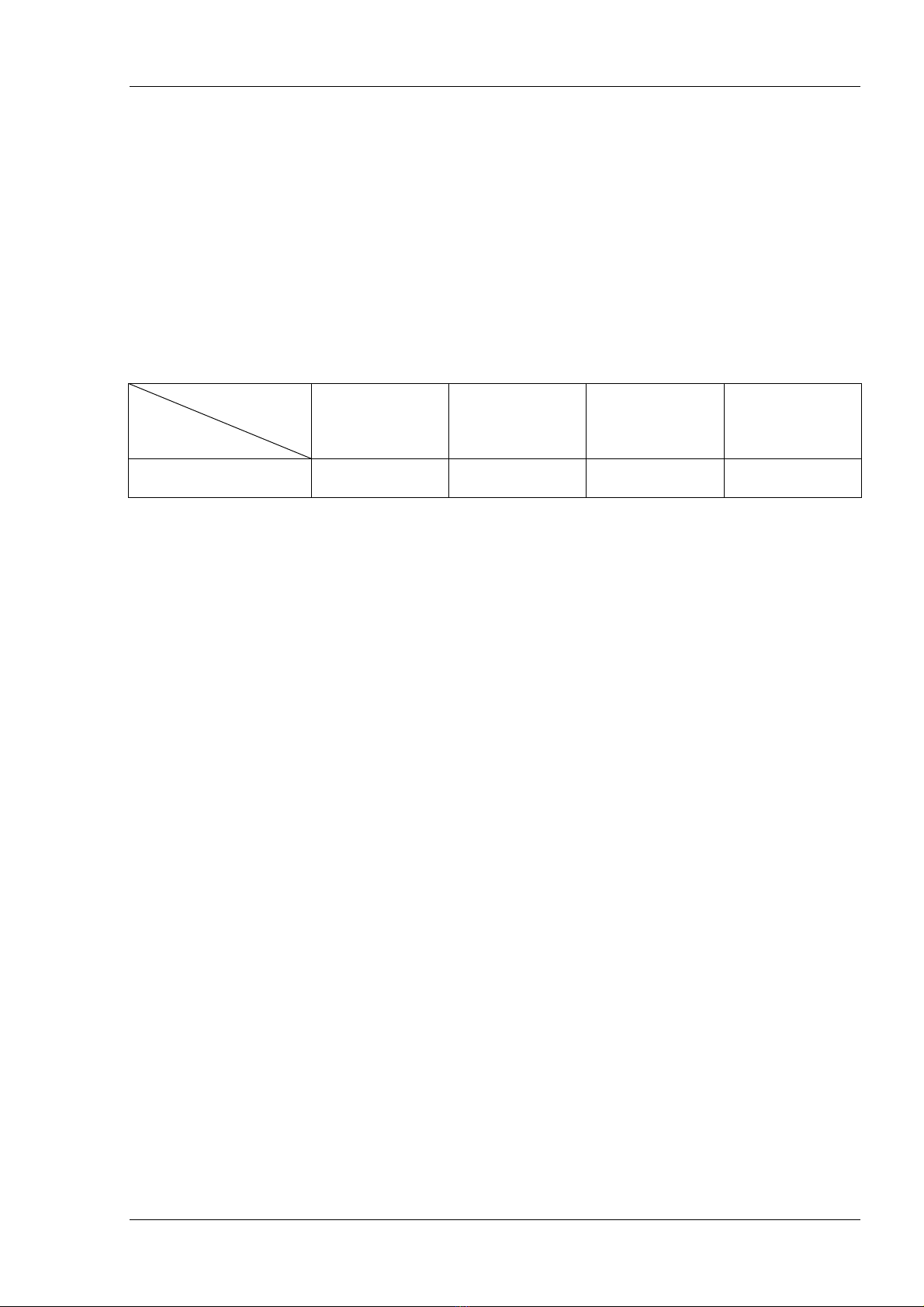
Năm 1999 2000 2001 2001

Chỉ tiêu

Gt sản xuất (tỷ đ) 10,0 10,5 11,2 12,0

Qua dãy số thời gian có thể nghiên cứu các đặc điểm về sự biến động của hiện

tượng,vạch dõ xu hường và tính quy luật của sự phát triển,đồng thời đề da dự đoán

các mức độ của hiện tượng trong tương lai.

Một dãy số thời gian được cấu tạo bởi hai thành phần là thời gian và chỉ tiêu về

hiện tượng nghiên cứu.thời gian có thể

là: Ngày, tuần, tháng, quý, năm…..độ dài giữa hai thời gian liền nhau được gọi là

khoảng cách thời gian.

Chỉ tiêu cề hiện tượng được nghiên cứu có thể là số tuyệt đối,số tương đối,số

bình quân.trị số của chỉ tiêu gọi là mức độ của dãy số.

Căn cứ vào đặc điểm của tồn tại về quy mô của hiện tượng qua thời gian có thể

phân biệt dãy số thời kì và dãy số thời điển.

Dãy số thời kỳ biểu hiện quy mô (khối lượng)của hiện tượng trong từng khoảng

thời gian nhất định .Trong dãy số thoàI kỳ các mức độ là những số tuyệt đối thời

kỳ,do đó độ dài của khoảng cách thời gian ảnh hưởng trực tiếp đến trị số của chỉ

tiêu và có thể cộng các trị số của chỉ tiêu để phản ánh quy mô của hiện tượng

4

Nguyễn Văn Thiệu

trong những khoảng thời gian dài hơn.

Đề án Lý thuyết thống kê

Dãy sồ thời đIểm biểu hiện quy mô(khối lượng ) của hiện tượng tại những thời

điểm nhất định. Mức độ của hiện tượng ở thời điểm sau thường bao gồm toàn bộ

hoặc một bộ phận mức độ của hiện tượng trước.vì vậy việc cộng các trị số của chỉ

tiêu không phản ánh quy mô của hiện tượng.

Yêu cầu cơ bản khi xây dựng một dãy số thời gian là phải đảm bảo tính chất có

thể so sánh được gữa các mức độ trong dãy số. Muốn vậy thí nội dung và

phương pháp tính toán chỉ tiêu qua thời gian phải thống nhất,phạn vi của hiện

tượng nghiên cứu trước sau phải nhát trị,các khoảng cách thời gian trong dãy số

nên bằng nhau(nhất là đối với dãy số thời kỳ).

Trong thực tế,do những nguyên nhân khác nhau,các yêu cầu trên cố thể bị vi

phạm,khi đó đòi hỏi phải có sự chỉnh lí thích hơp để tiến hành phân tích.để kết quả

thu được ,phân tích và nhận xét hiện tượng một cách chính xác và sát thực nhất.

2_Các chỉ tiêu phân tích dãy sồ thời gian

Để phản ánh đặc điểm biến động qua thời gian của hiện tượng được nghiên

cứu,người ta thường tính các chỉ tiêu sau đây:

2.1 mức độ trung bình theo thời gian

Chỉ tiêu này phản ánh mức độ đại biểu của các mức độ tuyệt đối trong dãy số

thời gian.tuỳ theo dãy số thời kỳ hoặc thời điểm mà có các công thức tính toán

khác nhau.

Đối với dãy số thời kỳ,mức độ trung bình theo thơi gian được tính theo công

n

y

......

+

+

+

i

y

y

y

n

1

2

y =

n

∑ i 1 == n

n ....3,2,1

)

=

thức sau:

iyi (

là các mức độ của dãy số thời kỳ. trong đó :

Đối với dãy số thời đIểm ó khoảng cách thời gian bằng nhau.ta tính theo công

n

1

.....

+

+

+

+

y

y

n

2

3

1 −

y 2

y 2

y

=

y n

1

−

5

Nguyễn Văn Thiệu

thức sau:

Đề án Lý thuyết thống kê

n ...3,2,1

)

=

iyi (

Trong đó là các mức độ của dãy sồ thời điểm có khoảng cách

thời gian bằng nhau.

Đối với dãy số thời điểm có khoảng cách thời gian không bằng nhau thì mức độ

n

i

∑

..........

+

+

ty

i

n

2

ty

ty

i

n

11

trung bình theo thời gian được tính bằng công thức sau đây.

1 = n

..........

+

+

n

1

2

+ t

ty 2 t +

..... t

i

∑

t

i

1 =

n ....3,2,1

)

y = =

it i = (

trong đó là độ dài thời gian có mức độ yi

2.2. Lượng tăng ( hoặc giảm) tuyệt đối

Chỉ tiêu này phản ánh sự thay đổi về mức độ tuyệt đối giữa hai thời gian

nghiên cứu,nếu mức độ của hiện tượng tăng lên thì trị số của chỉ tiêu mang dấu

dương(+) và ngược lại ,mang dấu âm(-).

Tuỳ theo mục đích nghien cứu,ta có các chỉ tiêu về lượng tăng (giảm) sau đây.

Lượng tăng (hoặc giảm)tuyệt đối liên hoàn(hay từng kỳ)là dấu hiệu giữa mức

)yi

1−i

)chỉ tiêu này phản ánh độ kỳ nghiên cứu ( và mức độ đứng liền trước nó( yi 1−

i ).

và thời gian mức tăng (hoặc giảm)tuyệt đối giữa hai kỳ liền nhau(thời gian

i

...3,2= n

Công thức tính như sau:

yy −

i

=δ

i

i

1−

( )

trong đó δi là lượng tăng (hoặc giảm)tuyệt đối liên hoàn.

Lượng tăng (hoặc giảm)tuyệt đối định gốc (hay tính dồn) là hiệu số giữa các

)và mức độ của một kỳ nào đó được chọn làm mức độ kỳ nghiên cứu( yi

n ...3,2

)

i =

)chỉ tiêu này phản ánh mức tăng gốc,thường là mức độ đầu tiên trong dãy số ( y1

i

=Δ

1

6

Nguyễn Văn Thiệu

( (hoậc giảm)tuyệt đối trong những khoảng thời gian dài.nếu ký hiệu Δi là các lượng tăng (hoặc giảm)tuyệt đối định gốc ta có: yyi −

Đề án Lý thuyết thống kê

n

3,2

,.....,

n

)

i =

i

i

∑ =

δ ( Δ

i

2

=

Dễ dàng nhận thấy rằng.

Tức là,tổng các lượng tăng (hoặc giảm) tuyệt đối liên hoàn bằng lượng tăng(hoặc

giảm)tuyệt đối định gốc :

Lượng tăng (hoặc giảm)tuyệt đối trung bình là mức trung bình của các lượng

tăng(hoặc giảm)tuyệt đối liên hoàn.nếu ký hiệu δ là lượng tăng (hoặc giảm)tuyệt

n

∑

−

i

1

δ

=

=

=

y n n

y 1

−

iδ 2 = 1 n −

Δ n n 1 −

đối trung bình,ta có:

2.3 Tốc độ phát triển

0 )phản ánh tốc độ và xu hướngbiến động của hiện tượng qua thời gian .tuỳ theo 0

Tốc độ phát triển là một số tương đối (thường được biểu hiện bằng lần hoặn

mục đích nghiên cứu,ta có các loại tốc độ phát triển sau đây.

Tốc độ phát triển liên hoàn phản ánh sự biến động của hiện tượng giữa hai

i

i (

3,2

....,

n

)

=

=

i

t

y y

i

1 −

1−i

thời gian liền nhau.công thức như sau:

:

1−i

Trong đó t i : tốc độ phát triển liên hoàn của thời gian i so vời thời gian

1yi −

mức độ của hiện tượng ở thời gian

: mức độ của hiện tưọng ở thời gian i yi

Tốc độ phát triểng định gốc phản ánh sự biến động của hiện tượng trong những

i (

n ,...3,2

)

=

i

=Τ

yi y

1

khoảng thời gian dài.công thức tính như sau:

7

Nguyễn Văn Thiệu

Trong đó :

Đề án Lý thuyết thống kê

tốc độ phát triển định gốc

:Τi yi

mức độ của hiện tượng ở thời gian i

:mức độ đầu tiên của dãy số y1

Giữa tốc độ phát triển liên hoàn và tố độ phát triển định gốc có các mồi liên

hệ sau đây:

Thứ nhất : tính các tốc độ phát triển liên hoàn bằng tốc dộ phát triển định gốc

....

n

2

3

tt .

nt

Τ=

i

....3,2= n

.tức là

i

it Τ=Π

( ) hay

Thứ hai : Thương của hai tốc độ phát triển định gốc liền nhau bằng tốc độ phát

triển liên hoàn giữa hai thời gian đó.

i

n ....3,2

)

=

=

it i (

i

1 −

Τ Τ

Tức là:

Tốc độ phát triển trung bình là trị số đại biểu của các tốc độ phát triển liên

hoàn.vì các tốc độ phát triển liên hoàn có quan hệ tích (như đã trinh bầy ở trên) nếu

để tính tốc độ phát triển bình quân,người ta sử dựng công thức số trung bình nhân.

n

1 −

t

..........

=

∏= n 1 −

2

3

n

i

tt .

t

t

n

n

n

nên

t

vì

=

−= n 1

n

i

= Τ∏ t

i

2

=

y y

y y

1

1

nếu ký hiệu t là tốc độ phát triển trung bình,thì công thức tính như sau

Từ công thức trên cho thấy :chỉ nên tính chỉ tiêu tốc độ phát triển trung bình

đối với nhữnh hiện tượng biến động theo một xu hướng nhất định

8

Nguyễn Văn Thiệu

2.4 Tốc độ (tăng) hoặc giảm

Đề án Lý thuyết thống kê

Chỉ tiêu này phản ánh mức độ của hiện tượng giữa hai thời gian đã tăng

(+)hoặc giảm(-)bao nhiêu lần (hoặc bao nhiêu phần trăm).Tương ứng với các tốc

độ phát triển,ta có các tốc độ tăng (hoặc giảm)sau đây.

)

n ...3,2

i =

Tốc độ tăng (hoặc giảm)liên hoan (hay từng ky)là tỉ số giữa lượng tăng(hoặc

( là tốc giảm) liên hoàn với mức độ kỳ gố liên hoàn : nếu ký hiệu ai

i

)

n ...3,2

i =

i

a

= δ ( y

i

1−

độ tăng (hoặc giảm) liên hoàn thì.

i

i

i

i

1 −

1 −

=

=

−

i

a

yy − y

y y

y y

i

i

i

1 −

1 −

1 −

1−

i

i

= ta

hay

(%)

(%)

100

−

i

i

a

= t

Nếu t i tính bằng phần trăm(%) thì

3,2

n ......

)

Tốc độ tăng (hoặc giảm)định gốc là tỷ số giữa lượng tăng (hoặc giảm )định

ii =Α (

là cá tốc độ tăng (hoặc gốc với mức độ kỳ gốc cố định.nếu ký hiệu

i

3,2

n ......

)

i =

giảm) định gốc thì.

i

Α =

Δ y

1

1−

(

i

i

= ΤΑ

(%)

(%)

100

−

hay

i

i

Α

= Τ

hoặc

tốc độ tăng (hoặc giảm)trung bình là chỉ tiêu phản ánh tốc độ tăng (hoặc

giảm)đại biểu trong xuốt thời gian nghiên cứu .

9

Nguyễn Văn Thiệu

Nếu ký hiệu ( a ) là tốc độ tăng (hoặc giảm) trung bình thì

Đề án Lý thuyết thống kê

a

1−= t

a

(%)

(%)

100

= t

−

hoặc

2.5. Giá trị tuyệt đối của 1(%) tăng (hoặc giảm)

Chỉ tiêu này phản ánh cứ 1(%) tăng (hoặc giảm) của tốc độ tăng (hoặc giảm)

3,2

n ........

)

i =

liên hoàn thì tương ứng với mmột trị số tuyệt đối là bao nhiêu. nếu ký hiệu

g i

( là giá tri tuyệt đối của 1(%)

i

3,2

n .......

)

i =

tăng (hoặc giảm) thì:

g

i

i

δ= (%)a

i

(

i

1 −

=

=

g

i

y i 1 − 100

i

= δ i a (%)

i

i

1 −

100.

yy − i yy − y

i

1 −

Việc tính toán chỉ tiêu này sẽ đơn giản hơn nếu ta biến đổi công thức trên :

Chú ý : chỉ tiêu này chỉ tính cho tốc độ tăng (hoặc giảm) liên hoàn, đối với tốc độ

tăng (hoặc giảm) định gốc thì không tính vì luôn là một số không đổi và bằng 1y 100

3-Một số phương pháp biểu hiện xu hướng biến đông cơ bản của hiện tượng

.

Sự biến động của hiện tượng qua thời gian chịu sự tác động của nhiều nhân

tố.Ngoài các nhân tố chủ yếu, cơ bản quyết định xu hướng biến động của hiện

tượng, còn có những nhân tố ngẫu nhiên gây ra những sai lệch khỏi xu hướng.xu

hướng thường được biểu hiện là chiều hướng tiến triển chung nào đó, một sự tiến

triển kéo dài theo thời gian, xác định tính quy lụât biến động của hiện tượng theo

thời gian. Việc xác định xu hướng biến động cơ bản cuỉa hiện tương có ý nghĩa

quan trọng trong nghiên cứu thống kê.vì vậy cần sử dụng những phương pháp

thích hợp ,trong một chừng mực nhất định, loại bỏ tác động của những nhân tố

10

Nguyễn Văn Thiệu

ngẫu nhiên để nêu nên xu hướng và tính quy luật về sự biến động của hiện tượng.

Đề án Lý thuyết thống kê

Sau đây sẽ trình bầy một số phương pháp thường được sử dụng để biểu hiện xu

hướng biến động cơ bản của hiện tượng

3.1 Phương pháp mở rộng khoảng cách thời gian

Phương pháp này được sử dung khi một dãy số thời kỳ có khoảng cách thời gian

tương đối ngắn và có nhiều mức độ mà qua đó chưa phản ánh được su hướng biến

động của hiện tượng.

Người ta có thể mở rộng khoảng cách thời gian tư tháng sang quý …do khoảng

cách thời gian được mở rộng nên trong mỗi mức độ của dãy số mới thì sự tác động

của các nhân tố ngẫu nhiên (với chiều hướng khác nhau) phần nào đã được bù trừ

(triệt tiêu) và do đó cho ta thấy xu hướng biến động cơ bản của hiện tượng.

3.2. Phương pháp số trung bình trượt (di động )

Số trung bình trượt (còn gọi là số trung bình di động )là só trung bình cộng của

một nhóm nhất định các mức độ của dãy số được tính bằng cách lấy lần lượt loại

dần các mức độ đầu, đồng thời thêm vào các mức độ tiếp theo,sao cho tổng số

,......

,

lượng cấc mức độ tham gia tính số trung bình không thay đổi.

yy ,

y

y

1

2

n

n

1 −

Giả sử có dãy số thời gian: nếu tính trung bình trượt cho nhóm

+

+

y

y

1

3

ba mức độ ,ta sẽ có :

y 2 3

+

+

y

y

2

4

3

= y 2

y 3

= y3

+

+

y

y

n

2

n

n

−

1 −

……

y 3

= y n 1−

Từ đó ta có một dãy số mới gồm các số trung bình trượt

11

Nguyễn Văn Thiệu

y 2 , y3 ,……. y n 1−

Đề án Lý thuyết thống kê

việc lựa trọn nhóm bao nhiêu mức độ để tính trung bình trượt đòi hỏi phải dựa

vào đặc điểm biến động của hiện tượng và số lượng các mức độ của dãy số thời

gian.

Nếu sự biến động của hiện tượng tương đối đều đặn và số lượng mức độ của dãy

số không nhiều thì có thể tính trung bìng trượt từ ba mức độ.

Nếu sự biến động của hiện tượng lớn và dãy số có nhiều mức độ thì có thể tính

trung bình trượt từ năm hoặc bẩy mức độ. Trung bình trượt càng được tính từ

nhiều mức độ thì càng có tác dụng san bằng ảnh hưởng của các nhân tố ngẫu

nhiên.nhưng mặt khác lại làm giảm số lượng các mức độ của dãy trung bình trượt.

Nếu số lưọng mức độ của dãy số trung bình trượt quá ít,thì ảnh hưởng đền

nghiên cứu xu hướng cơ bản

3.3. Phương pháp hồi quy

Trên cơ sở dãy số thời gian,người ta tìm một hàm sồ(gọi là phương trình hồi

quy) phản anh sư biến động của hiện tượng qua thời gian có dạng tổng quát như

,

,.........

)

t

sau:

n

0

1

aa ,

a

= f( yt

,

........

: mức độ lý thuyết trong đó: yt

n

0

1

2

aaa ,

a

: các tham số

t : thứ tự thời gian

Để lựa chọn đúng đắn dạng của phương trình hồi qui đồi hỏi phải dựa vào sự

phân tích đặc điểm , biến động của hiện tượng quá thời ,đồng thời kết hợp với một

(giảm) tuyệt đối , dựa vào tốc độ phát triển …)

2,1

.......,

)

n

=

số phương pháp đơn giản khác (như dựa vào đồ thị , dựa vào sự tăng

iai (

∑(

−

thường được xác định bằng phương pháp bình phương các tham số

y

y

t

t

nhỏ nhất , tứclà : ) =min

12

Nguyễn Văn Thiệu

Sau đây là một vài dạng phương trình hồi qui đơn giản thường được sử dụng :

Đề án Lý thuyết thống kê

Phương trình đường thẳng:

0

1

taa +

= yt

Phương trìng đường thẳng được sử dụng khi các lượng tăng ( hoặc giảm)

(hay còn gội là sai phân bậc một ) xấp xỉ bằng nhau . tuyệt đối liên hoàn δi

Áp dụng phương pháp bình phương nhỏ nhất sẽ có hệ phương trình sau đây

n

t

y =∑

∑+ 1

0

aa

2

ty =∑

1

0

a t

ta ∑+∑

để xác định giá trị của tham số a0 và a1 :

Phương trình parabol bậc hai :

Phương trình parabol bậc hai được sử dụng khi các sai phân bậc hai (tức là các

,.......,

sai phân của sai phân bậc 1) xấp xỉ nhau

n

0

1

aa ,

a

2

n

y =∑

1

0

2

aa

ta t ∑+∑+

2

3

ty =∑

2

1

0

a t

tata ∑+∑+∑

2

3

2

4

∑

=

2

1

0

t y

tatata ∑+∑+∑

Các tham số được xác định bởi hệ phương trình sau đây:

0

1

Phương trình hàm mũ :

= aa t yt

Phương trình hàm mũ được sử dụng khi các tốc độ phát triển xấp xỉ bằng

nhau

0

1

aa ,

lg

lg

lg

y

n

t

∑

=

+

∑

0

1

a

a

2

t

lg

y

lg

lg

∑

=

+∑

0

1

a t

ta ∑

Các tham số được xác định bơỉ hệ phương trình sau đây :

o

Ta thấy rằng : biến t là biến thứ tự thời gian , tacó thể thay t bằng t’ (nhưng

t =∑ /

vẫn đảm bảo thứ tự ) sao cho thì việc tính toán sẽ đơn giản hơn

13

Nguyễn Văn Thiệu

Có hai trường hợp :

Đề án Lý thuyết thống kê

Thứ nhất: nếu thứ tự thời gian là một số lẻ thì lấy thời gian ở giữa bằng 0 , các

thời gian đứng đằng trước là -1,-2 –3 ,,,và các thời gian đứng sau lần lượt là

1,2,3,….

Thứ hai : Nếu thứ tự thời gian là một số chẵn thì lấy hai thời gian đứng ở giữa là -

1 và 1, cácthời gian đứng trước lần lượt là -3, -5,…

o

Và đứng sau lần lượt là 3,5 …

t =∑ /

/

/

n

y

y =∑

=

0

ao

a =⇒

y ∑ n

/

∑

/

/

/

y

∑

2 =⇒∑=

y 2

1

1

t

ta

a

t t ∑

/

/

/

1

taa 0 +

Với tổng thì hệ phương trình trên sẽ là :

14

Nguyễn Văn Thiệu

khi đó: yt / =

Đề án Lý thuyết thống kê

3.4. Phương pháp biểu hiện biến động thời vụ

Sự biến động của một số hiện tượng kinh tế xã hội thường có tính thời vụ

nghĩa là hằng năm trong thời gian nhất định , sự biến động được lặp đi lặp lại .

Ví dụ : các sản phẩm của ngành nông nghiệp phụ thuộc vào từng thời vụ . Trong

các ngành khác như công nghiệp , xây dựng , giao thông vận tải , dịch vụ , …đều

ít nhiều có biến đọng thời vụ . Nguyên nhân gây ra biến động thời vụ là do ảnh

hưởng của các điều kiện tự nhiên ( thời tiết , khí hậu ) và do phong tục tập quán

sinh hoạt của dân cư .

Biến động thời vụ làm cho hoạt động của một số ngành , khẩn trương ; lúc thì

nhàn rỗi bị thu hẹp lại

Nghiên cứu biến động thời vụ nhằm đề ra những chủ trương , biện pháp phù

hợp, kịp thời , hạn chế những ảnh hưởng của biến dộng thời vụ đến sản xuất và

sinh hoạt của xã hội

Nhiệm vụ của nghiên cứu thống kê là dựa vào số liệu của nhiều năm (ít nhất

là 3 năm ) để xác đinnhj tính chất và mức độ của biến động thời vụ . Phương pháp

thường được sử dụng là tính các chỉ số thời vụ .

Trường hợp biến động qua những thời gian của các năm tương đối ổn định ,

không có hiện tượng tăng( giảm) rõ rệt thì chỉ số thời vụ được tính theo công thức

.

100

100

i =Ι

i =Ι

yi 0y

yi 0y

sau đây :

Trong đó :

Ιi Ιi : chỉ số thời vụ của thời gian t.

y

: số trung bình các mức độ của các thời gian cùng tên i. yi yi

y0

0

15

Nguyễn Văn Thiệu

: số trung bình của tất cả các mức độ trong dãy số .

Đề án Lý thuyết thống kê

Trường hợp biến động thời vụ qua những thời gian nhất định của các tham số thì

n

y

∑

Þ

i

1 =

100

=

i

Ι

y ih n

chỉ số thời vụ được tính theo công thức sau đây :

Trong đó :

: mức độ thực tế ở thời gian I năm thứ j y Þ

: .mức độ tính toán (có thể là số trung bình trượt hoặc dựa vào phương yij

trình hồi qui ở thời gian i của năm j )

n: số năm nghiên cứu .

4. Dự đoán thống kê .

4.1. Khái niệm về dự đoán thống kê

4.1.1 Dự đoán thống kê ngắn hạn: là dự đoán quá trình tiếp theo của hiện tượng

của những khoảng thời gian tương tương đối ngắn , nối tiếp với hiện tại bằng việc

sử dụng những thông tin thống kê và áp dụng những phương pháp thích hợp .

4.1.2 Các loại dư báo , tầm dự báo (thời gian dự báo )

Có baloại:

- Dự báo ngắn hạn : dưới 3 năm .

- Dự báo trung hạn : từ 3 đến 7 năm .

-Dự báo dài hạn : trên 10 năm .

Thường thì tầm dự báo càng xa , mức độ chính xác càng kém .

4.1.3 Các phương pháp dự đoán

Phương pháp chuyên gia : xin ý kiến các chuyên gia về lĩnh vực đó . Trên cơ

sở đó sử lý ý kiến và đưa ra dự đoán

(

,.......,

)

f

~ y =

Phương pháp hồi qui ( phương pháp kinh tế lượng ) xác định mô hình hồi qui

1

2

n

xx ,

x

nhiều biến

16

Nguyễn Văn Thiệu

Phương pháp mô hình hoá dãy số thời gian :

Đề án Lý thuyết thống kê

f

)(t

=

yt

17

Nguyễn Văn Thiệu

Đề án Lý thuyết thống kê

4.1.4 Dự đoán thống kê

Thống kê đơn vị nghiên cứu thông kê khônh những biêt điều phải xảy ra ,

mà còn phải biết những điều tương lai của hiện tượng

Dự đoán thống kê là phần rất quan trọng của nghiên cứu thống kê

Làm dự đoán thống kê có khả năng thực hiện được các loại dự đoán . Chú

trọng nhất là dự đoán thống kê ngắn hạn .

Dự đoán thống kê cần phải có tài liệu để tiến hanh dự đoân thống kê . . Dãy số

thời gian sử dụng phương pháp phù hợp để đưa ra những dự đoán có cơ sở khoa

học chính xác và các mức độ có thể có thể so sánh được trong dãy số thời gian

Độ dài của các dãy số thời gian , số lượng dãy số thời gian càng dài càng tốt chí

một số ít các mức cuối dãy

Từ đó phân tích đặc điểm biến động của hiện tượng qua thời gian , tầm dự doán

dưới 1/3 độ dài thời gian của cá hiện tượng .

4.2 Một số phương pháp đơn giản để dự đoán thống kê ngắn hạn

4.2.1Dự đoán dựa vào lượng tăng (giảm ) tuyệt đối bình quân

Phương pháp dự đoán này có thể được sử dụng khi các lượng tăng (giảm) tuyệt

đối liên hoàn xấp xỉ nhau.

−

1

Ta đã biết lượng tăng giảm tuyệt đối bình quân được tính theo công thức:

y n n

y 1

−

δ=

=

δ+

từ đó ta có mô hình dự đoán:

y

hnˆ y

n

+

h (h=1,2,3…n)

:y n

mức độ cuối cùng của dãy số thời gian. Trong đó

4.2.2 Dự đoán dựa vào tốc độ phát triển trung bình.

Phương pháp dự đoán này được áp dụng khi các tốc độ phát triển liên hoàn

xấp xỉ nhau

18

Nguyễn Văn Thiệu

Ta đã biết tốc độ phát triển trung bình được tính theo công thức:

Đề án Lý thuyết thống kê

n

y y

1

t = 1 −n

Trong đó:

: mức độ đầu tiên của dãy số thời gian y1

: mức độ cuối cùng của dãy số thời gian y n

từ mô hình trên ta có thể dự đoán theo.

=

( )h ty

n

y hnˆ +

4.2.3 Dự đoán dựa vào phương trình hồi quy

,.........

...,

Ta đã có phương trình hồi quy theo thời gian

0

1

n )

aa ,

a

=f(t, yt

,

,........

)

f

t (

h

=

+

có thể dự đoán bằng cách ngoại suy phương trình hồi quy:

ˆ y

0

1

n

aa ,

a

ht +

,.........

...

2,1=h

trong đó :

t + ) h

mức độ dự đoán ở thời gian( y htˆ +

f +

4.2.4

t

s

t

)

h

=

+

+

4.2.4.1 Dạng cộng Dự đoán dựa vào hàm xu thế và biến động thời vụ =ˆ y

ˆ y

0

j

bb t (1 +

c

ht +

Từ đó ta có mô hình dự đoán

Để lập được phương trình hàm xu thế và biến động thời vụ ta tiến hành phân tích

(

−

) Τ

=

1

b

s m

1 n + 2 m

)1

−

1

=

0

1

b

mn + 2

m

m

1

1

j

)

j

j

)

(

(

−

−

−

=

y −−

−

y

j

1

1

c

b

b

j

+ 2

12 2 mn n ( Τ mn b − = Τ n

Τ nm

+ 2

19

Nguyễn Văn Thiệu

các thành phần theo dạng cộng.

Đề án Lý thuyết thống kê

j

,.........

m

2,1=

20

Nguyễn Văn Thiệu

Đề án Lý thuyết thống kê

*

ˆ = y

f

t

s

t

t

4.2.4.2 Dạng nhân

Mô hình dự đoán:

*

=

y

f

t

t

zs x

t

t

Phân tích các thành phần kết hợp nhân

.thường xây dựng trên dãy số trung bình trượt(thường Xác định hàm xu thế f t

trượt bốn mức dộ với tài liệu quý,trượt 12tháng với tài liệu tháng ).

t

=

t

t

zs *

y f

t

Xác định các thành phần thời vụ .

t )

Tính trung bình xén(trung bình xén được tính bằng cách loại bỏ giá trị lớn

y f

t

nhất và nhỏ nhất của tỷ số

Tính hệ số điều chỉnh:

H = Error!

Chỉ số thời vụ đIều trỉnh của thời gian j = trung bình xén j *H

4.3 Dự đoán bằng phương pháp san bằng mũ.

không có biến động thời vụ 4.3.1 Mô hình giản đơn Mô hình này được sử dụng khi dãy số thời gian yt

α

)ˆ α

1( −+

=

và xu thế(hay biến động và xu thế không rõ ràng).

y

y

t

t

t

+

=

(1) Ta có:

y

y βα + t

t

t

ˆ 1 y +ˆ 1 y

1

≤ βα

, ≤

(2) đặt 1-α= βta có

là các tham số san bằng và 0 βα,

và mức là trung bình cộng gia quyền của các mức độ thực tế yt Như vậy ytˆ 1+

β

=

độ dự đoán ytˆ

ˆ y

t

1

−y α + t

ytˆ 1−

21

Nguyễn Văn Thiệu

Tương tự ta có: (3)

Đề án Lý thuyết thống kê

βαα

+

=

−+

y

β2

tˆ 1 y

t

+

1ˆ −yt

ytˆ 1−

n

i

i

1 +

Thay (3) vao(2)ta có: (4)

y ββα

ytˆ 1−

t

t

i

1ˆ y + ∑=

−

0

i

=

∞

1

Ο→

βα = <1 nên i → ∞ thì

(5) ……ta có

+β 1i

iβα →∑

0

=i

∞

i

và vì 1-

y

t

t

1ˆ y + ∑= βα

1 −

i

0

=

)

( α

=

+

−

khi đó

ˆ y

y

ˆ y

ˆ 1 y

t

t

t

t

+

từ (1) ta có

α

) α

=

1( −+

ˆ y

y

ˆ y

t

1

t

t

+

(

t

=

)( t

α

α

=

1( −+

4.3.2 Mô hình xu thế tuyến tính không biến động thời vụ (Holt)

0

y

ˆ) y

0

a

a

ˆ y t

1

+

t

t

t )(

=

) với

0

1

a

1ˆ yt

+

t (

t )(

t (

α

=

1( −+

)1 +−

−

])1

y

0

0

1

t a )( + [ a ) α

a

a

t

t )(

t )(

t (

)1

t (

)1

) ϕ

=

−

−

1( −+

−

]

1

0

0

1

a

[ a ϕ

a

a

1

, ≤

≤ ϕα

Mô hình của H

)0(

=

là các tham số san bằng o ϕα,

y

0

a

1

chọn điều kiện ban đầu

)0(1a

là lượng tăng giảm tuyệt đối trung bình

4.4 Dự đoán dựa vào mô hình tuyến tính ngẫu nhiên(phương pháp Box-

Jenkins)

4.4.1 Một số mô hình dừng

Để mô tả các mô hình ta sử dụng một số toán tử sau đây : toán tử chuyển

=

dịch về phía trước(B)

y

y

t

t

1−

m

y

y =Β

t

mt −

∇

=

−

B

y

y

y

t

t

t

1−

d

d

1 −

d

1(

=

) β−

y

y

y

∇

∇= ∇

t

t

t

22

Nguyễn Văn Thiệu

Toán tử sai phân

Đề án Lý thuyết thống kê

Mô hình tự hồi quy bậc (p)-ký hiệu AR(P)

..........

=

+

+

+

+

t

t

t

p

1

2

2

1 −

−

pt −

t

a

z

z

z

z

Φ

Φ

Φ

,.....

,

Mô hình tổng quát:

2

1

p

ΦΦΦ

Trong đó: là các tham số

] 0 =

t

kt

a

t

−aa ,

] 0=at

p

2

..........

)

−

−

] s 2= Biểu diễn toan tử B: (1-

p

2

1

t

ay =

ΒΦΦ −Β

ΒΦ

t

at là một quá trình đặc biệt đơn giản thường gọi là nhiễu,với: ;Cov[ E[ :Var[ a

t

ay =

Φ ) ( p B

t

........

+

+

+

Hay

ρ

ρ

1

2

p

ρρ Φ =

Φ

Φ

k

k

k

2

1 −

−

pk −

0

=

Hàm tự tương quan

Φ ρk B ) (

Hay

..........

−

−

−

t

t

1

2

2

t

t

q

1 −

−

qt =

a

a

a θθ

θ −

= az

2

q

1(

..........

.....

)

=

−

t

2

q

t

a

θθ −Β− 1

θ −

z

Β

Β

,

..........

....

Mô hình trung bình trượt bậc q-ký hiệu MA(q)

2

1

3

q

θθθ ,

θ

với là các tham số

....

−

+

k

qk +

hàm tự tương quan

ρk

1

....

1 +

+

+ θθ q 2 θ q

+ θθθ k 1 + 2 θ 1

= với k = 1…n

0 với k ≥ q + 1

Mô hình hỗn hợp bậc p,q ký hiệu ARMA(p,q)

Là sự kết hợp giữa mô hình tự hồi quy bậc p và mô hình trung bình trượt bậc q

Zt = Φ1Zt-1 + ……. + Φp Zt-p + at - Φ1at-1 - … Φqat - q

= Zt - Φ1Zt-1 - …. - Φp Zt-p = at - Φ1at-1 - …. - Φqat-q

23

Nguyễn Văn Thiệu

Φ (B)Zt = Φ(B)at

Đề án Lý thuyết thống kê

4.42 Phương pháp luận Box-Jenkins

Được tiến hành qua các bước sau

Bước 1: Chọn mô hình tốt nhất,là mô hình cố SEmin

Bước 2:Ước lượng các tham số của mô hình đã chọn .phương pháp sử dụng

như:phương pháp bình phương nhỏ nhất,hợp lí tối đa…..

t

Τ= ,1

Bước 3:Kiểm tra các giá trị của mô hình đã được xác định

)(ˆ hyt

h

+Τ

E

,

.......... .

=

=

Bước 4:Dự đoán: Gọi với là dự đoán của y ht +

Ta có

[

]

)(ˆ y h

y

y

y

Τ

ht +

1 −Τ

y y

Τ

⎤ ⎥ ⎥ 1 ⎦

⎡ ⎢ ⎢ ⎣

1(

−

=

1

∇ΒΦ )

yt

1

= 1(

+

+

1-

t

1

a

t

yt

yt 1 −Φ 1)

1

1

1(

+

=

-

1

1

y ht

2

1

+

1

1(

=

+

=

+

-

]−

)ˆ y ht −+Φ ]

-

[

)(ˆ y h

y

h

+Τ

ˆ ˆ −θ - a ht - at 1 −+θ ˆ +a ht + - a ht −+θ ] [ a

1

h 2

1

h

+Τ

Τ

Ví dụ dự đoán một mô hình ARIMA(1,1,1) )ˆ Βθ at 1ˆ y +Φ 2 1ˆ y ht −+Φ ] [ )ˆ y ht −+Φ

[ 1ˆ y −+ΤΦ

] [ 1ˆ a h 1 −+ΤΦ

24

Nguyễn Văn Thiệu

Đề án Lý thuyết thống kê

CHƯƠNG II

VẬN DỤNG LÝ THUYẾT DÃY SỐ THỜI GIAN ĐỂ PHÂN TÍCH BIẾN

ĐỘNG TỔNG DOANH THU CỦA CÔNG TY TNHH THIẾT BỊ GIẶT LÀ

CÔNG NGHIỆP (TỪ NĂM 1996-2003 VÀ DỰ BÁO 2004)

I- THỰC TRẠNG CỦA CÔNG TY

1 - Thực trạng

Ngày nay ,với xu thế hội nhập và mở cửa .kinh tế việt nam trong những năm

gần đây phát triển rõ dệt, đời sống của người dân ngày càng cao. Nhu cầu về sinh

hoạt cũng như chăm sóc, bảo hiểm, y tế ,càng phát triển ,đIều đó dẫn đến nhu cầu

về các thiết bị máy móc: như máy giặt là, máy sấy …đựơc dùng trong sinh hoạt

hàng ngày trong gia đìng và đặc biệt ở trong các cơ sở y tế ( bệnh viện ,phòng

ngiên cứu ..) ngày càng lớn .Đầu tư vào lĩnh vực buôn bán thiết bị giặt là thực sự

mới mẻ ,song nó cũng đáp ứng do nhu cầu tạo ra.

Với số dân hơn 80 triệu người ;mức sống dân cư dần được nâng cao .Cho nên

đầu tư vào lĩnh vưc này cũng sẻ tạo ra cho chúng ta nhiều cơ hội mới, tuy nhiên

do nền kinh tế thị trừơng ,xu hứng hội nhập và toàn cầu hoá hiện nay ,việc buôn

bán mặt hàng này gặp phải không ít khó khăn như: ro đời sống chưa thực sự tốt

,nhu cầu về mặt hàng nay thực sự chư nhiều ,đồng thời gặp phảI sự cạnh tranh của

các đối thủ cạnh tranh khác .Vốn và các mối làm ăn của ta, cũng như kỹ thuật thiết

bị sẽ phải gặp các đối thủ canh tranh rát mạnh cùng xâm nhập trong thị trường nội

địa. Các sản phẩm của Công ty chưa thực sự có khả năng canh tranh cao về kỹ

năng tính dụng cũng như là về giá cả.

Điều khó khăn đặc biệt là sự cạnh tranh giá cả hiện nay, tính năng đa dạng,

gọn nhẹ và tiện nghi hợp thời trang, xong phảI phù hợp với giá cả thị hiếu và đứng

vững trên thị trường.

Tuy nhiên với những thách thức còn nhiều. Song công ty luôn tìm cách khắc

25

Nguyễn Văn Thiệu

phục, hoàn thành các chỉ tiêu đề ra. Liên tục mức tổng doanh thu hàng quý trong

Đề án Lý thuyết thống kê

giai đoạn gần đây. Mức tăng trung bình 239,2844triệu VND đảm bảo sự phát triển

và tăng trưởng của công ty cả về quy mô, vốn cũng như là lợi nhuận. Trung bình

hàng quý tốc độ phát triển trung bình 107,26% vượt kế hoạch 7,26%.

Như vậy, tình hình kinh doanh của công ty là có khả quan và pphát triển theo chiều

hướng tốt tạo nhiều cơ hội mới trong kinh doanh.

2. Xu hướng phát triển của tổng doanh thu.

Những năm gần đây, hoạt động kinh doanh của công ty đã có sự tăng

trưởng vượt bậc. Mặc dù công ty được thành lập không lâu. Mới được 8 năm, song

sự tăng về mức doanh thu cũng như lợi nhuận của công ty liên tục đạt kế hoạch,

làm ăn có lãI ngày một nhiều. Qui mô cơ sở ngày càng khang trang, đồng thời

quy mô tàI sản, vốn của công ty tăng nhanh 8%/quý. Về mức độ tăng doanh thu

tuyệt đối 16,87triệu VND/quý.

Sự kinh doanh của công ty tập trung phần lớn là hợp đồng ký kết với các cơ

sở, bệnh viện, trạm y tế trong nước. Đây là phần thu lớn cảu hoạt động kinh doanh

của công ty. Bên cạnh đó làm nhà phân phối chính cho các đạI lý ở các thành phố

lớn cũng như tỉnh lỵ đã đáp ứng nhu cầu của tầng lớp dân cư thành thị có mức thu

nhập cao cũng chiếm một tỷ trọng lớn.

Với xu thế phát triền hội nhập hiện nay, tình hình kinh tế liên tục phát triển

đời sống thu nhập của dân cư ngày càng được nâng cao. Cho nên đầu tư vào lĩnh

vực phục vụ thị hiễu sinh hoạt của tầng lớp dân cư có mức thu nhập cao ngày càng

được đề cập đến. Nhu cầu của khách hàng sẽ cao và tăng nhanh trong những năm

gần đây đIều đó khẳng định chiều hướng kinh doanh của công ty trong những năm

tới sẽ ngày càng phát triển mở rông, ngày càng tăng nhanh quy mô cũng như môI

mặt của hoạt động kinh doanh. Tổng doanh thu ngày càng tăng bình quân khoảng

26

Nguyễn Văn Thiệu

8%/quý.

Đề án Lý thuyết thống kê

II. VẬN DỤNG LÝ THUYẾT VÀO THỰC TẾ

Tài liệu về tổng doanh thu bán hàng của Công ty TNHH

THIẾT BỊ GIẶT LÀ CÔNG NGHIỆP 1996 - 2003 như sau:

Đơn vị: triệu VNĐ

Quý Quý I Quý II Quý III Quý IV Năm

1996 60 120 118 123,5

1997 70 126,5 128,5 171,4

1998 80 162,5 171,1 159,5

1999 103 203,5 207 145

2000 108 227 206 232,6

2001 163 201 404 407

2002 275 457 464 354

2003 258 487 573 582

1117 2025 2268,1 2237 ∑

(Số liệu trên được lấy từ Phòng Tài vụ của Công ty tại trụ sở

Số 17, ái Mộ Nguyễn Ngọc Lâm, Long Biên, Hà Nội)

1. Phân tích biến động qua thời gian của tổng doanh thu từ 1996 - 2003

1.1. Phân tích các chỉ tiêu dãy số thời gian

7648,1 1.1.1. Mức độ trung bình theo thời gian 32 ∑yi i=1 y = = = 239,003125 (triệu VNĐ) 32 32

1.1.2. Lượng tăng (giảm) tuyệt đối

• Lượng tăng (giảm) tuyệt đối từng quý (kỳ) (δi)

δ2 = y2 - y1 = 120 - 60 = 60 (triệu VNĐ)

δ3 = y3 - y2 = 118 - 120 = - 2 (triệu VNĐ)

δ4 = y4 - y3 = 123,5 - 118 = 5,5 (triệu VNĐ)

27

Nguyễn Văn Thiệu

• Lượng tăng (giảm) tuyệt đối định gốc (Δi)

Đề án Lý thuyết thống kê

Δ2 = y2 - y1 = 120 - 60 = 60 (triệu VNĐ)

Δ3 = y3 - y1 = 118 - 60 = 58 (triệu VNĐ)

Δ4 = y4 - y1 = 123,5 - 60 = 63,5 (triệu VNĐ)

• Lượng tăng giảm tuyệt đối trung bình:

32 ∑ δi i=1

582 - 60 522 y32 - y1 Δ32

= 16,8387 = = = = δ = 32 - 1 32 - 1 32 - 1 32 - 1 31 (triệu VNĐ)

1.1.3. Tốc độ phát triển

• Tốc độ phát triển liên hoàn

t2 = Error! = Error! = 2 (lần) = 200(%)

• Tốc độ phát triển định gốc:

T2 = Error! = Error! = 2 (lần) = 200 (%)

T3 = Error! = Error! = 1,9666 (lần) = 196,66 (%)

• Tốc độ phát triển trung bình:

n-1;Π ti = Error! = Error! = Error! = 1,0726 (lần) = 107,26 (%)

t =

1.1.4. Tốc độ tăng (hoặc giảm)

• Tốc độ tăng (hoặc giảm) liên hoàn (từng kỳ) (ai)

ai = Error! => a2 = t2 - 1 = 2 - 1 = 1 (lần) = 100%

• Tốc độ tăng (hoặc giảm) định gốc (Ai)

Ai = Error! -> A2 = T2 - 1 = 2 - 1 = 1 (lần) = 100(%)

A3 = T3 - 1 = 1,9666 - 1 = 0,9666 (lần) = 96,6(%)

• Tốc độ tăng (hoặc giảm) trung bình: ( a )

a = t - 1 -> a = 1,0726 - 1 = 0,0726 = 7,26 (%)

1.1.5. Giá trị tuyệt đối của 1% tăng (hoặc giảm) (gi)

gi = Error! = Error! => g2 = Error! = Error! = 0,6 (triệu VNĐ)

tương tự

g3 = Error! = Error! = 1,2 (triệu VNĐ)

28

Nguyễn Văn Thiệu

g4 = Error! = Error! = 1,18 (triệu VNĐ)

Đề án Lý thuyết thống kê

29

Nguyễn Văn Thiệu

…………

Đề án Lý thuyết thống kê

Các chỉ tiêu tính toán ở trên sẽ được cho ở bảng sau:

t

yt

ti (%)

Ti (%)

ai (%) Ai (%)

δi

Δi

gi (triệu VNĐ) -

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

60,00 120,0 118,0 123,50 70,00 126,50 128,50 171,40 80,00 162,50 171,10 159,50 103,00 145,00 203,50 207,00 108,00 227,00 206,00 232,60 163,00 301,00 404,00 407,00 275,00 257,00 464,00 354,00 258,00 487,00 573,00 582,00

- 60,00 -2,00 5,50 -53,50 56,50 2,00 42,90 -91,40 82,50 8,60 -11,60 -56,50 42,00 58,50 3,50 -99,50 119,00 -21,00 26,60 -69,60 138,00 103,00 3,00 -132,00 182,00 7,00 -110,00 -96,00 229,00 86,00 9,00

- 60,00 58,00 63,50 10,00 66,50 68,50 114,40 20,00 102,50 111,10 99,50 43,00 85,00 143,50 147,00 48,00 167,00 146,00 172,60 103,00 241,00 344,00 347,00 215,00 397,00 404,00 294,00 198,00 427,00 513,00 522,00

- 200,00 98,33 104,66 56,68 180,71 101,58 133,38 46,67 203,12 105,29 93,22 64,57 140,77 140,34 101,72 52,17 210,18 90,75 112,91 70,07 184,66 134,22 100,74 67,56 166,18 101,53 76,29 72,88 188,76 117,66 101,57

- 200,00 196,66 205,83 116,66 210,83 214,17 285,67 133,33 270,83 285,17 265,83 171,67 241,67 339,17 345,00 180,00 378,33 343,33 387,67 271,67 501,67 673,33 678,33 458,33 761,67 773,33 590,00 430,00 811,67 955,00 970,00

- 100,00 1,67 4,66 -43,32 80,71 1,58 33,38 -53,33 103,12 5,29 -6,78 -35,43 40,77 40,34 1,72 -47,83 110,18 -9,25 12,91 -29,93 84,66 34,22 0,74 -32,44 66,18 1,53 -23,71 -27,12 88,76 17,66 1,57

- 100,00 96,66 105,83 16,66 110,83 114,17 185,67 33,33 170,83 185,17 165,83 71,67 141,67 239,17 245,00 80,00 278,33 243,33 287,67 171,67 401,67 573,33 578,33 358,33 661,67 673,33 490,00 330,00 711,67 855,00 870,00

1,200 1,180 1,235 1,700 1,265 1,285 1,714 0,800 1,625 1,711 1,595 1,030 1,450 2,035 2,070 1,080 2,270 2,260 2,326 1,630 3,010 4,040 4,070 2,750 4,750 4,640 3,540 2,580 4,870 5,730 5,820

(Bảng 1)

Nhận xét: Qua phân tích các dãy số thời gian ở trên. Cũng như kết quả được

tính ở (bảng 1) cho chúng ta thấy:

Mức độ tổng doanh thu trung bình hàng quý trong giai đoạn (1996-2003) là

239,2844 (triệu VNĐ).

Tổng doanh thu trung bình hàng quý trong 8 năm: 16,8387 (triệu VNĐ).

30

Nguyễn Văn Thiệu

Trung bình hàng quý trong giai đoạn (1996-2003) tốc độ phát triển trung

Đề án Lý thuyết thống kê

bình 107,26%.

Giá trị tổng doanh thu tăng trung bình hàng quý 7,26%.

Như vậy, tình hình kinh doanh của Công ty TNHH Thiết bị Giặt là Đông Á

là khả quan, và phát triển theo chiều hướng tốt.

1.2. Hồi quy theo thời gian

Sự biến động của hiện tượng theo thời gian chịu tác động của nhiều nhân tố.

Các nhân tố tác động vào hiện tượng và xác lập xu hướng phát triển cơ bản. Có

nhiều cách để xác định xu hướng phát triển của hiện tượng.

Sau đây là phương pháp: Hồi quy theo thời gian.

Biểu diễn các mức độ tổng doanh thu của dãy số thời gian bằng một mô hình

hồi quy theo thời gian.

Để xác định giá trị cụ thể của các tham số trong mô hình người ta thường

dùng phương pháp bình phương nhỏ nhất.

Có nhiều mô hình hồi quy theo thời gian, để biểu diễn các mức độ tổng

doanh thu theo thời gian như: hàm bậc nhất, hàm xu thế bậc hai, hàm xu thế bậc

ba, hàm xu thế mũ...

Do đó ta phải lựa chọn một mô hình biểu diễn tốt nhất xác định xu hướng

phát triển cơ bản của tổng doanh thu qua các năm từ 1996 đến 2003 của Công ty

TNHH Thiết bị Giặt là Đông Á.

Mô hình hồi quy theo thời gian tốt nhất là mô hình có SEmin.

31

Nguyễn Văn Thiệu

Qua số liệu tính toán ở (bảng 2). Ta xây dựng các mô hình tuyến tính.

Đề án Lý thuyết thống kê

1.2.1. Mô hình tuyến tính

t4

t3

t*yt

yt 60,00 120,00 118,00 123,50 70,00 126,50 128,00 171,40 80,00

t2 T 1 1 2 4 3 9 4 16 5 25 6 36 7 49 8 64 9 81 10 162,50 100 11 171,10 121 12 159,50 144 13 103,00 169 14 145,00 19 15 203,50 225 16 207,00 256 17 108,00 289 18 227,00 324 19 206,00 361 20 232,60 400 21 163,00 441 22 301,00 484 23 404,00 529 24 407,00 576 25 275,00 625 26 457,00 676 27 464,00 729 28 354,00 784 29 258,00 841 30 487,00 900 31 573,00 961 582,00 1024 32 528 7648,10 11440

lg(y) T*lgy 1,7781 1,7781 2,0791 4,1582 2,0718 6,2154 2,0916 8,3664 1,4851 9,2255 2,1021 12,6126 2,1089 14,7623 2,234 17,8720 1,9031 17,1279 2,2108 22,108 2,2332 24,5652 2,2027 26,4324 2,0128 26,1664 2,1643 3,02582 2,3085 34,6275 2,3159 37,0544 2,0034 34,5678 2,356 42,408 2,3138 43,9622 2,3666 47,332 2,2121 46,4541 2,4785 54,527 2,6063 59,9449 2,6095 62,628 2,4393 60,9825 2,6599 69,1574 2,6665 71,9955 2,509 71,372 2,4116 69,9364 2,6875 80,625 2,7581 85,5011 88,4768 2,7649 73,572 1283,201

t2*yt 60,00 60,00 1 1 240,0 480,00 16 8 354,00 1062,00 81 27 494,00 1976,00 256 64 350,00 1750,00 625 125 759,00 4554,00 1296 216 899,50 6296,50 2401 343 1371,20 10969,60 4096 512 720,00 6480,00 6561 729 1625,00 16250,00 10000 1000 1882,10 20703,10 14641 1331 1914,00 22968,00 20736 1728 1339,00 17407,00 28561 2197 2030,00 28420,00 38416 1744 3052,50 45787,50 50625 3375 3312,00 52992,00 65536 4096 1836,00 31212,00 83521 4913 4086,00 73548,00 10476 5832 3914,00 74366,00 130321 6859 4652,00 93040,00 160000 8000 3423,00 194481 71883,00 9261 6622,00 234256 145684,00 10648 9292,00 279841 213716,00 12167 9768,00 331776 134432,00 13824 6425,00 390625 171875,00 15625 11882,00 456976 308932,00 17576 12528,00 532441 338256,00 19683 9912,00 614656 277536,00 21952 7482,00 707281 216978,00 24389 1460,00 810000 438300,00 27000 17763,00 29791 923521 550653,00 32768 1048576 540672,00 18624,00 163221,30 278874 7246096 4019238,70 (Bảng 2)

ŷt = a + bt

Ta có:

7648,1 = 32.a + 528.b

163221,3 = 528a + 11440.b ∑yt = n.a + b∑t ∑t.yt = a∑t + b∑t2

Giải hệ phương trình ta được:

32

Nguyễn Văn Thiệu

a = 15,0474 b = 13,5731

Đề án Lý thuyết thống kê

Do đó: ŷt = 15,0474 + 13,5731.t

Thay t vào mô hình, ta tính được ŷt; yt - ŷt ; SSE1

(tính ở bảng 3)

1.2.2. Mô hình Parabol bậc 2 ŷt = a + bt + ct2

7648,1 = 528b + 32a + 1140c

163221,3 = 528a + 11440b + 278784c

Ta có: ∑yt = na + b∑t + c∑t2 ∑t.yt = a∑t + b∑t2 + c∑t3 ∑t2yt = a ∑t2 + b ∑t3 + c ∑t4 4019238,7 = 11440a + 278784b + 7246096c

Giải hệ phương trình ta được: b = 2,3432

a = 78,6819

c = 0,3403

ŷt = 78,6818 + 2,3432t + 0,3403 t2 Do đó: Thay tt vào mô hình, ta tính ŷt ; yt - ŷt ; SE2

(tính ở bảng 3)

1.2.3. Mô hình hàm mũ

ŷt = abt

Ta có:

73,527 = 32lga + 528 lgb

1283,2012 = 528lga + 11440 lgb ∑ lg yt = n lga + lgb ∑t ∑t lgyt = lga ∑t + lgb ∑t2

Giải hệ ta được: a = 74,868 . 1,0608t

33

Nguyễn Văn Thiệu

Thay t vào mô hình, ta tính ŷt ; yt - ŷt ; SE3

Đề án Lý thuyết thống kê

t

yt

ŷt

(yt - ŷt)2

P/trình đường thẳng (yt - ŷt)2

P/trình hàm mũ ŷt

(yt - ŷt)2

P/trình Parabol ŷt 81,3653 984,6730 88,7741 6053,8358 93,4994 3872,9836 98,9053 2933,3272 104,9918 166,7429 84,7294 900,8401 14,7584 340,0667 119,2075 2281,7627 3272,4463 127,3349 137,3959 136,1438 145,6333 155,8034 166,6541 190,3973 190,3973 319,4680 216,8629 231,1166 246,0509 261,6478 277,9613 294,9374 312,5941 330,9314 349,9493 369,6478 390,0269 411,0866 432,8269 455,2478 478,3493 502,1314

60,00 28,6205 120,00 42,1936 118,00 55,7667 123,50 69,3398 70,00 82,9128 126,50 96,4860 128,50 110,0591 171,40 123,6322 80,00 137,2053 162,50 150,7784 45,5422 171,10 164,3515 339,4658 159,50 177,9246 7831,8429 103,00 191,4977 3608,5010 145,00 205,0708 229,3377 203,50 218,6439 207,00 232,2170 635,8970 108,00 245,7901 18986,1116 1047,3767 227,00 259,3632 4480,4682 206,00 272,9363 232,60 286,5094 2906,2234 163,00 300,0825 18791,6118 160,1642 301,00 313,6556 5893,8325 404,00 327,2287 4382,2016 407,00 340,8018 6300,3747 275,00 354,3749 7930,2587 457,00 367,9480 6802,7689 464,00 381,5240 354,00 259,3632 8956,1239 258,00 408,6673 22700,6352 487,00 422,2404 4193,8057 573,00 435,8135 18820,1357 582,00 449,3866 17586,3138 183572,9674

611,5453 975,0568 600,2794 604,8992 1224,4260 456,4760 280,2644 2724,0570 2240,5927 694,6492 648,5528 13,6648 4051,8444 2060,9148 171,6807 12647,8813 11851,1310 16,9463 1604,0745 843,7746 13216,1005 36,7551 8355,0385 5786,4319 5617,3957 7630,4068 5472,1195 3258,8799 30564,4449 1008,2022 8958,7550 6378,9932 140886,2551

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 528 7648,10

377,1354 79,4199 1278,1548 84,2487 1488,2620 79,4222 836,6947 94,5743 934,4588 100,5689 392,6932 106,6835 235,0129 113,1698 2636,7613 120,0505 2212,7702 127,0400 751,1692 135,0925 772,4976 143,3061 55,9627 152,0191 3394,4534 161,2619 679,4709 171,0666 485,4302 181,4675 210,2284 192,5000 7140,3754 192,5007 107,7352 216,6204 566,0098 229,7909 124,5958 243,7622 9136,1092 258,5829 274,3048 712,6314 290,9825 12772,9378 9667,9397 308,6743 327,4417 2750,1336 347,3501 12023,0846 9126,1598 368,4690 390,8719 1359,5430 414,6369 24535,1494 439,8469 2223,4121 466,5896 11323,1686 7576,2626 494,9582 127886,4037

(bảng 3)

Lúc này để lựa chọn mô hình chính xác nhất ta so sánh SE. Dựa vào bảng 3,

32

ta có:

i=

SE = Error! với SSE = ∑ (yt - ŷt)2

34

Nguyễn Văn Thiệu

183572 Ta được: SE1 = 9674;32 - 2 = 78,2246

Đề án Lý thuyết thống kê

140886 SE2 = 2551;32 - 3 = 69,7004

127886 SE1 = 4037;32 - 2 = 65,2907

Như vậy trong ba mô hình hồi quy trên thì mô hình 3 là mô hình có SE nhỏ

nhất. Vì vậy ta sẽ chọn mô hình 3.

Vậy có MH xu thế : ŷt = 74,868 . 1,0606t

1.3. Phân tích các thành phần của dãy số thời gian

Có 3 thành phần: (ft) xu thế , (St) thời vụ , (zt) ngẫu nhiên

(ft): xu thế: nói lên xu hướng phát triển của hiện tượng kéo dài theo thời

gian t

(St): thời vụ: biến động mang tính chất lặp đi lặp lại trong một thời gian nhất

định (thường là một năm)

(zt): ngẫu nhiên.

1.3.1. Phân tích các thành phần kết hợp cộng (Bảng Buys-Ballof B-B)

t ≡ Sj

(t = 1, 2, ... nxm) yt = ft + St + zt ŷt = b0 + b1t + S0

Từ tài liệu đã có, ta tính các tham số (bảng 4)

Quý (j)

Quý I

Quý II Quý III Quý IV

Ti

iTi

Năm i

1996

1

60

120

118

123,5

421,5

421,5

1997

2

70

126,5

128,5

171,4

496,4

992,8

1998

3

80

162,5

171,1

159,5

573,1

1719,3

1999

4

103

145

203,5

207

658,5

2634

2000

5

108

227

206

232,6

773,6

3868

2001

6

163

301

404

407

1275

7650

2002

7

275

457

464

354

1550

10850

2003

8

258

487

573

582

1900

15200

1117

2026

2268,1

2237

T = 7648,10

S = 43335,60

Tj

139,625

253,250

283,512 279,625 y = 239,003

yj

35

Nguyễn Văn Thiệu

Đề án Lý thuyết thống kê

(Bảng 4)

Kết quả tính toán từ bảng 4, ta có:

= Error!. Error! - Error!. 7648,1 b1 = Error! Error! - Error!* T

= 13,2725 (triệu VNĐ/tháng)

b0 = Error! - b1 Error! = Error! - 13,2725 . Error!= 20,0068 (triệu VNĐ)

Sj = yj - y - b1 (j - Error!)

S1 = yj - y - b1 (j - Error!) = 139,625 - 239,003 - 13,2725 (1 - Error!) = -79,4692

S2 = 253,250 - 239,003 - 13,2725 (2 - Error!) = 20,88325 (triệu VNĐ)

S3 = 283,512 - 239,003 - 13,2725 (3 - Error!) = 37,87275 (triệu VNĐ)

S4 = 279,625 - 239,003 - 13,2725 (4 - Error!) = 20,71325 (triệu VNĐ)

S1 = -79,4692 (triệu VNĐ)

Suy ra: ŷt = 20,0068 + 13,2725t + Si S2 = 20,88325 (triệu VNĐ)

S3 = 37,87275 (triệu VNĐ)

S4 = 20,71325 (triệu VNĐ)

Nhận xét: S1 < 0 , (S2; S3; S4) > 0

Như vậy, tổng doanh thu quý I nhìn chung giảm. Còn các quý khác (quý II,

quý III, quý IV) tổng doanh thu đều tăng.

1.3.2. Phân tích các thành phần kết hợp nhân

yt = f(t) . S(t) . Z(t)

Theo trên ta đã tìm được hàm xu thế: f(t) = 20,0068 + 13,2725t. (Xác định

hàm xu thế f(t). Thường xây dựng trên dãy số trung bình trượt. Trượt 4 mức độ với

tài liệu quý, trượt 12 mức độ với tài liệu tháng).

Xác định thành phần thời vụ: St . Zt = Error!

Đi tính trung bình xén: Được tính bằng cách loại bỏ giá trị Max và Min của

tỷ số Error!

Tính hệ số điều chỉnh:

H = Error!

Chỉ số thời vụ điều chỉnh của thời gian j bằng trung bình xén j x H

36

Nguyễn Văn Thiệu

Xác định Zt : Zt = Error! . St

Đề án Lý thuyết thống kê

(Các kết quả được thể hiện ở bảng 5 và bảng 6)

S(t)

y(t) 60,00 120,00 118,00 123,50 70,00 126,50

t 1 2 3 4 5 6

f(t) 33,2793 46,5518 59,8243 73,0968 86,3693 99,6418

Error! 1,8029 0,6525 2,5777 1,1083 1,9724 1,1582 1,6895 1,0806 0,8104 0,6525 1,2695 1,1083

S(t) 2,7630 2,3258 1,7029 1,5634 1,2419 1,1454

128,50

7

112,9143

1,1380 1,1582

0,9825

171,40 80,00 162,50 171,10 159,50 103,00 145,00 203,50 207,00 108,00 227,00 206,00 232,00 163,00 301,00 404,00 407,00 275,00 457,00 464,00 354,00 258,00 487,00 573,00 582,00

8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

126,1868 139,4593 152,7318 166,0043 179,2768 192,5493 205,8218 219,0943 232,3668 245,6393 258,9118 272,1843 285,4568 2987293 312,0018 325,2743 338,5468 351,8193 365,0918 378,3643 391,6368 404,9093 418,1818 431,4543 444,7268

1,3583 1,0806 0,5736 0,6525 1,0639 1,1083 1,0306 1,1582 0,8896 1,0806 0,5349 0,6525 0,7044 1,1083 0,9288 1,1582 0,8908 1,0806 0,4369 0,6525 0,8767 1,1083 0,7568 1,1582 0,8127 1,0806 0,5465 0,6525 0,9647 1,1083 1,2420 1,1582 1,2021 1,0806 0,7816 0,6525 1,2517 1,1083 1,2263 1,1582 0,9038 1,0806 0,6371 0,6525 1,1645 1,1083 1,1581 1,328 1,1872 1,0806

1,2569 0,879 0,9599 0,8898 0,8232 0,8197 0,6355 0,8019 0,8243 0,6737 0,791 0,7151 0,752 0,8375 0,8704 1,0723 1,1124 1,1978 1,1293 1,0587 0,8363 0,9763 1,0507 1,1466 1,0986

37

Nguyễn Văn Thiệu

(bảng 5)

Đề án Lý thuyết thống kê

Quý

Quý I

Quý II

Quý III Quý IV

Năm

1,8029

2,5777

1,9724

1,6895

1996

0,8104

1,2695

1,1380

1,3583

1997

0,5736

1,0693

1,0306

0,8896

1998

0,5349

0,7044

0,9288

0,8908

1999

0,4396

0,8767

0,7568

0,8127

2000

0,5465

0,9647

1,2420

1,2021

2001

0,7816

1,2517

1,2263

0,9038

2002

0,6371

1,1645

1,3280

1,1872

2003

TB xén

0,64735

1,09940

1,14895

1,07196

(bảng 6)

Từ bảng 6 ta tính được hệ số điều chỉnh

H = Error! = Error! = 1,0081

Tính chỉ số thời vụ: Sj = TB xén j . H

S1 = 0,64735 * 1,0081 = 0,65259

S2 = 1,09940 * 1,0081 = 1,10830

S3 = 1,14895 * 1,0081 = 1,15825

S4 = 1,07196 * 1,0081 = 1,08064

Nhận xét: Ta thấy S1 = 0,65259 < 0, còn các (S2, S3, S4) > 0 nên cho ta kết

luận: Quý I tổng doanh thu nhìn chung là giảm. Còn các quý II, quý III, quý IV đều

có tổng doanh thu tăng.

2. Dự báo các quý năm 2004

Như phần lý thuyết đã trình bày để dự báo các quý của nămt ới ta có thể dựa

vào các phương pháp sau:

- Dự báo dựa vào lượng tăng (giảm) tuyệt đối trung bình. Song điều kiện để

áp dụng MH này là các lượng tăng (giảm) tuyệt đối liên hòan xấp xỉ bằng nhau.

38

Nguyễn Văn Thiệu

Dựa vào (bảng 1), ta thấy không nên áp dụng mô hình này.

Đề án Lý thuyết thống kê

Dự báo dựa vào tốc độ phát triển trung bình. Điều kiện áp dụng phương

pháp này là các tốc độ phát triển liên hoàn xấp xỉ nhau. Dựa vào (bảng 1) ta thấy

cũng không nên áp dụng phương pháp này.

Như vậy ta nên áp dụng phương pháp hàm xu thế.

2.1. Dự báo dựa vào hàm xu thế

Theo phần trên, ta đã tìm được MH hàm xu thế tốt nhất

ŷt = 74,868 . 1,0608t

Mô hình dự báo sẽ là:

Quý I t = 33 :

Quý II t = 34 :

Quý III t = 35 :

Quý IV t = 36 : ŷ33 = 74,868 . (1,0608)33 = 525,0517 ŷ34 = 74,868 . (1,0608)34 = 556,9748 ŷ35 = 74,868 . (1,0608)35 = 590,8389 ŷ36 = 74,868 . (1,0608)36 = 626,7619

2.2. Dự báo dựa vào hàm xu thế và biến động thời vụ

2.2.1. Dự báo dựa vào bảng B.B (kết hợp cộng)

Mô hình: ŷt = ft + Sj

S1 = -79,4692

ŷt = 20,0068 + 13,2725t + Sj S2 = 20,8832

S3 = 37,8727

S4 = 20,7132

Quý I: t = 33 - ŷ33 = 20,0068 + 13,2725 . 33 - 79,4692 = 378,5301 (triệu VNĐ)

Quý II: t = 34- ŷ34 = 20,0068 + 13,2725 . 34 + 20,8832 = 492,1550 (triệu VNĐ)

Quý III: t = 35-ŷ35 = 20,0068 + 13,2725 . 35 + 37,8727 = 522,4170 (triệu VNĐ)

Quý IV:t = 36- ŷ36 = 20,0068 + 13,2725 . 36 + 20,7132 = 528,5300 (triệu VNĐ)

2.2.2. Dự báo dựa vào xu thế kết hợp nhân

Mô hình: ŷt = ft . St

0,6525

Ta có: ŷt = (20,0068 + 13,2725t)*St 1,1083

1,1582

39

Nguyễn Văn Thiệu

1,0806

Đề án Lý thuyết thống kê

Quý I: t = 33: ŷ33 = (20,0068 + 13,2725*33)*0,6525 = 298,8445 (triệu VNĐ)

Quý II: t = 34: ŷ34 = (20,0068 + 13,2725*34)*1,1083 = 522,3105 (triệu VNĐ)

Quý III: t = 35: ŷ35 = (20,0068 + 13,2725*35)*1,1582 = 561,199 (triệu VNĐ)

Quý IV: t = 36: ŷ36 = (20,0068 + 13,2725*36)*1,0806 = 537,9408 (triệu VNĐ)

Mô hình 1

Mô hình 2

yt

-46,1899 67,4350 97,6970 93,8100 6,9001 120,5250 143,7870 146,9000 59,9901 173,6150 203,8770 199,9900 113,0801 226,7050 256,9670 253,0800 166,1701 279,7950 310,0570 306,1700 219,2601 332,8850 363,1470 359,2600 272,3501 385,9750 416,2370 412,3500 325,4401 439,0650 469,3270 465,4400

ŷt

t 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

60,00 120,00 118,00 123,00 70,00 126,50 128,50 171,40 80,00 162,50 171,10 159,50 103,00 145,00 203,50 207,00 108,00 227,00 206,00 232,60 163,00 301,00 404,00 407,00 275,00 457,00 464,00 354,00 258,00 487,00 573,00 582,00

(yt - ŷt)2 ŷt 21,7147 1465,7640 51,5933 4679,4766 69,2885 2372,8102 78,9884 1937,0209 186,1614 56,3559 258,1484 110,4330 130,7773 5,1860 136,3790 1226,4704 120,9362 90,9971 45,8681 169,2726 192,2661 448,0037 193,7265 1171,4533 125,6384 512,4971 228,1123 6907,6544 253,7550 2525,5650 251,0955 1944,4131 160,2796 2733,1565 286,9519 3594,2303 315,2438 11934,2078 308,4646 5755,4375 194,9208 1018,9374 345,7915 2006,2784 376,7326 743,5111 365,8336 1694,6724 229,5620 2064,6118 404,6312 2742,4912 438,2215 664,5310 423,2027 4789,0136 38,4809 264,2033 463,4708 553,6232 499,7103 5371,3801 480,5717 10287,7000 81799,6911

(yt - ŷt)2 11276,2948 2763,0792 412,2118 852,0561 3981,5973 35,7006 233,6923 600,2500 400,3960 123,5432 1074,3317 1639,4401 101,6084 6675,7070 2858,7200 2123,3664 3383,7605 2787,3120 10827,8592 5412,5445 3165,1988 1016,6532 1668,9676 2279,1076 7,0219 5044,5506 2281,3041 3404,7225 4548,1670 2297,7642 10748,0909 13586,2336 107341,2552 (Bảng 7)

Trong 2 phương pháp dự đoán ta có:

40

Nguyễn Văn Thiệu

Mô hình cộng có: SE1 = Error!= Error! = 60,8393

Đề án Lý thuyết thống kê

Mô hình nhân có: SE2 = Error! = Error! = 53,1100

Như vậy trong các mô hình, mô hình dự báo kết hợp nhân là chính xác nhất

vì mô hình có SE nhỏ nhất.

Nhận xét: Có được kết quả trên là do công ty đã tận dụng tốt mọi lợi thế so

sánh để phát triển công cuộc tiêu thụ sản phẩm, đa dạng hóa sản phẩm, liên tục

nâng cao kỹ năng các sản phẩm để đáp ứng thị hiếu của khách hàng. Đồng thời quá

trình quảng bá sản phẩm của công ty là đúng đối tượng, nắm bắt được nhu cầu của

khách hàng. Bên cạnh đó nghiên cứu về giá cả của công ty là rất hợp lý. Làm cho

sức cạnh tranh sản phẩm của công ty đáng kể so với lúc mới thành lập công ty.

Công ty đã tích cực đầu tư, nâng cấp điều kiện phục vụ khách hàng, áp dụng

tốt các quy trình kinh doanh.

Trong năm 2003, trước những khó khăn thách thức mới công ty đã không

ngừng cải tổ phương thức kinh doanh và nâng cao chiến dịch quảng bá sản phẩm

của công ty. Như hàng năm công ty chi hàng tỷ đồng đẻ mở rộng các cơ sở, đại lý

của hàng của công ty toàn bộ các tỉnh miền Bắc. Ngoài ra công ty còn liên tục hợp

tác lưu thông nhập các linh kiện, phụ tùng của các nước có thiết bị hiện đại như

Mỹ, Trung Quốc, Nhật Bản...

Tuy nhiên hiện nay, công ty vẫn gặp phải nhiều khó khăn. Để đẩy mạnh việc

tăng doanh thu, nhằm đạt tới mục tiêu 298,845 triệu VNĐ/quý I; 522,3105 triệu

VNĐ vào quý II; 561,199 triệu VNĐ vào quý III và 537,9408 triệu VNĐ vào quý

IV vào năm 2003 và tăng hơn nữa vào các quý trong những năm tiếp theo. Công ty

cần phải chú trọng vào các vấn đề như: liên tục phải nâng cao tính năng, mẫu mã

sản phẩm. Đa dạng hóa chủng loại máy móc. Giá cả phải hợp lý. Công ty cần phải

chủ động quy hoạch và phát triển thị trường, chú trọng đề ra chiến lược Marketing

phù hợp. Các thị trường trọng yếu này phải cân nhắc và xem xét kỹ khi đưa ra các

41

Nguyễn Văn Thiệu

quyết định kinh doanh.

Đề án Lý thuyết thống kê

42

Nguyễn Văn Thiệu