SỞ GIÁO DỤC & ĐÀO TẠO
HÀ TĨNH
ĐỀ CHÍNH THỨC
KỲ THI CHỌN HỌC SINH GIỎI TỈNH CẤP THPT
NĂM HỌC 2011-2012
MÔN TOÁN LỚP 10
Thời gian làm bài 150 phút
( Đề thi có 01 trang, gồm 4 câu)
Câu 1. a) Giải phương trình: 2
7 10 2 2
x x x
.
b) Giải hệ phương trình:
2 2
2
2 2 3
2 2 4
x y x y
y xy x
.
Câu 2. Tam giác ABC có độ dài các cạnh là a, b, c và có diện tích bằng 1.
Chứng minh rằng: 2 2 2
2012 2010 1005 4 2010
a b c .
Câu 3. a) Xác định hình dạng tam giác ABC biết các góc A, B, C của tam giác
đó thỏa mãn hệ thức: sin
2
cos
C
SinA B
.
b) Cho hình thoi ABCD, biết đường thẳng AB, AC lần lượt có phương
trình 2x – y + 7 = 0, 3x – y + 8 = 0 và đường thẳng BC đi qua điểm
M(-4;
13
2
). Lập phương trình đường thẳng CD.
Câu 4. Các số thực x, y, z dương thỏa mãn điều kiện: x + y + z =
3
2
. Tìm giá trị
nhỏ nhất của biểu thức: M = 2 2 2 2
2 2
4 1 4 1 4 1
x xy y y yz z
z zx x
yz zx xy
.
------------------------------------------Hết--------------------------------------------------
- Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
- Giám thị không được giải thích gì thêm.
Họ và tên thí sinh: ……………………………………………………………
Số báo danh :………………………………………………………………….
SỞ GD & ĐT HÀ TĨNH ĐỀ THI CHỌN HỌC SINH GIỎI TỈNH
LỚP 10 THPT NĂM 2011
ĐỀ CHÍNH THỨC Môn: Vật lý
Thời gian làm bài: 150 phút
Bài 1: Quả cầu nhỏ ( được xem là chất điểm) có khối lượng m = 500 gam được treo vào điểm cố
định 0 bằng dây treo mảnh, nhẹ, có chiều dài L = 1,0 m. Kéo quả cầu tới vị trí dây treo tạo với
phương thẳng đứng góc
rồi buông nhẹ. Lấy g = 10m/s2. Bỏ qua mọi ma sát
1) Cho
= 900. Hãy xác định lực căng dây, vận tốc và gia tốc của quả cầu khi nó đi qua vị trí mà
dây treo tạo với phương thẳng đứng góc
= 300.
2) Khi quả cầu qua vị trí cân bằng, dây treo vướng đinh ở điểm I cách 0 một khoảng b = 0,7m.
Xác định góc
để quả cầu thực hiện được chuyển động tròn trong mặt phẳng thẳng đứng quanh I
Bài 2:
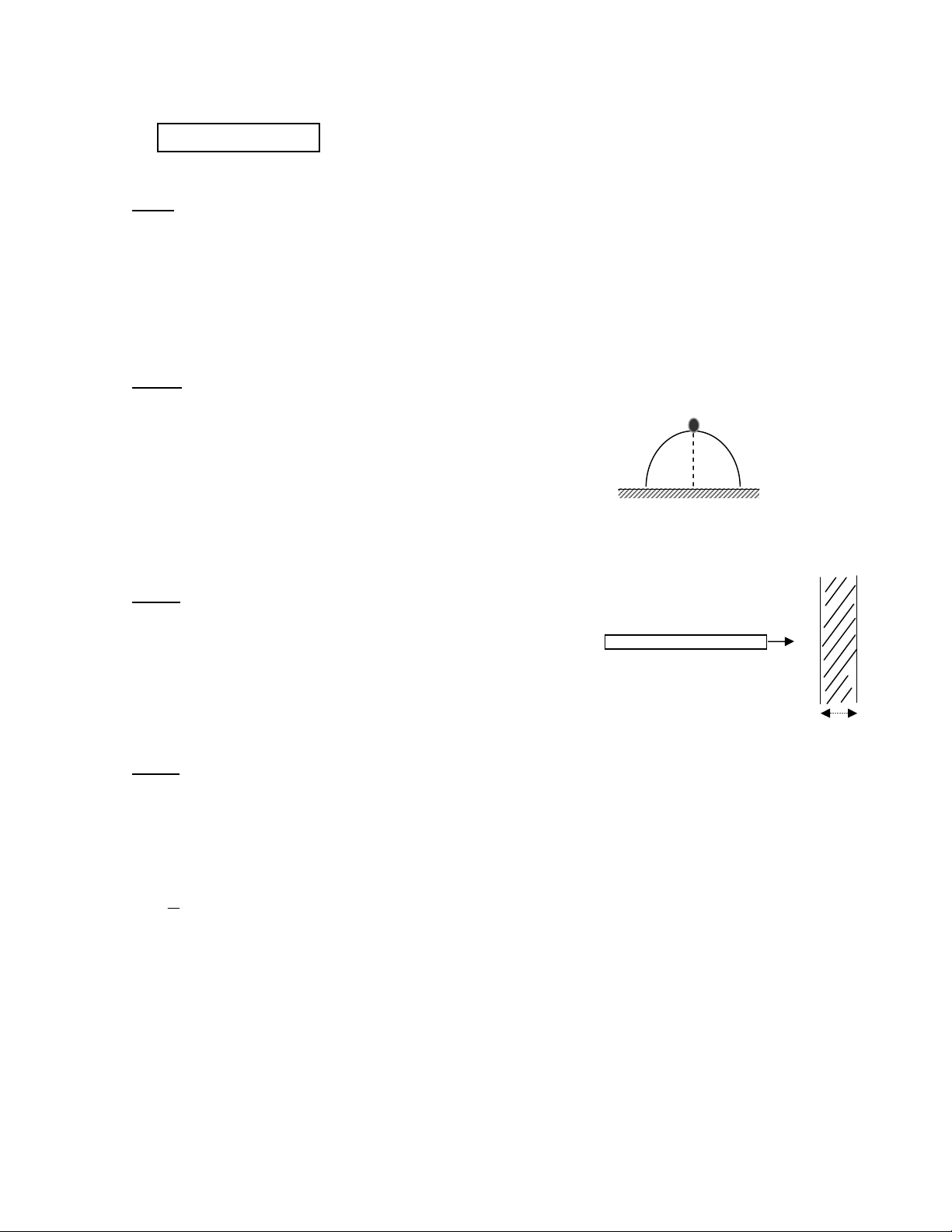
Một vật dạng bán cầu
,
bán kính R
được đặt trên
mặt phẳng nằm ngang. Trên đỉnh bán cầu có đặt một vật
nhỏ khối lượng m (xem hình 1).Vật m bắt đầu trượt xuống
với vận tốc ban đầu không đáng kể. Bỏ qua ma sát giữa
vật m và bán cầu. Tìm vị trí vật m bắt đầu rời khỏi bán cầu
trong hai trường hợp:
1) Bán cầu được giữ cố định.
2) Bán cầu có khối lượng M = m và có thể trượt không
ma sát trên mặt phẳng nằm ngang.
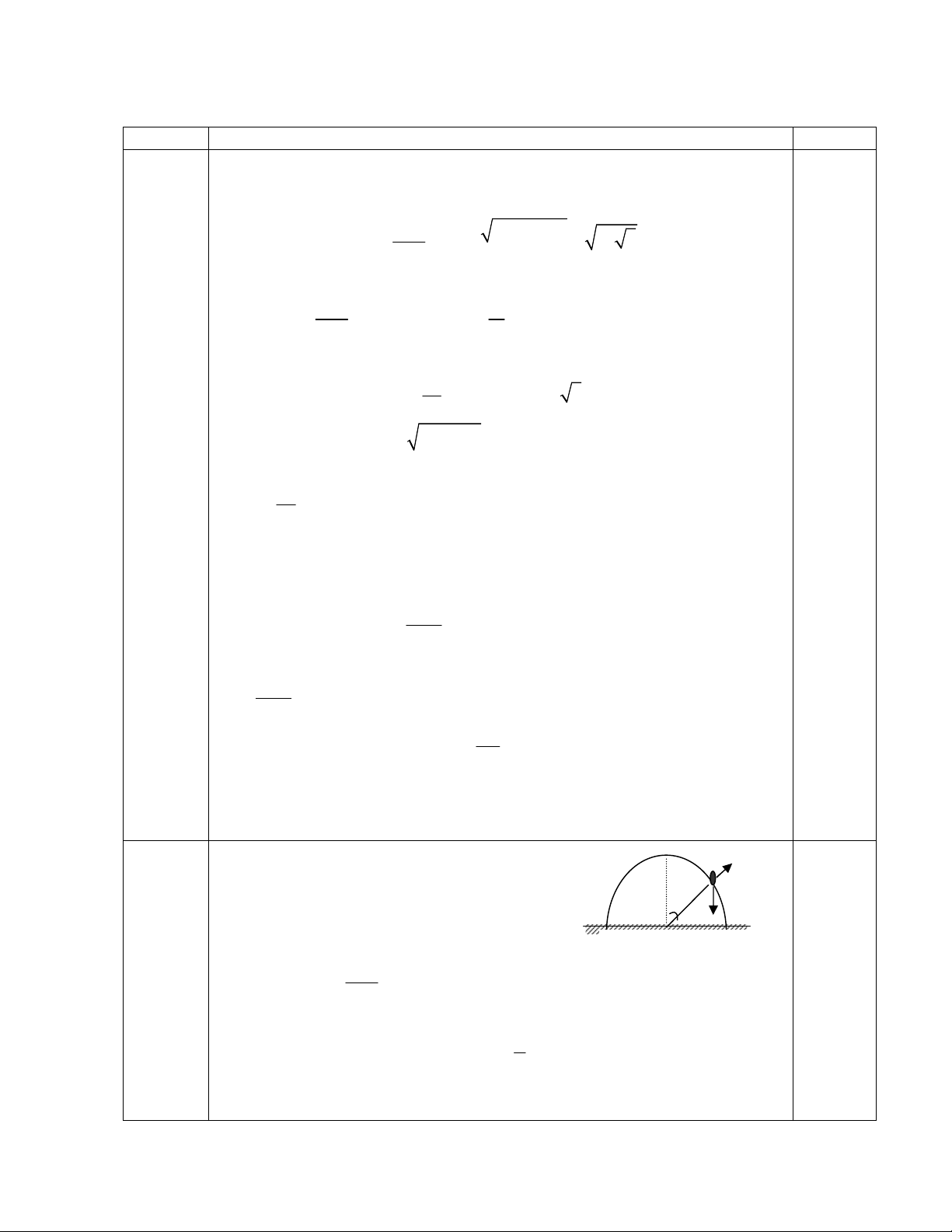
Bài 3: Một ván trượt dài L = 4m, khối lượng phân bố đều
theo chiều dài, đang chuyển động với vận tốc v0 = 5m/s
trên mặt băng nằm ngang thì gặp một dải đường nhám có
chiều rộng l = 2m vuông góc với phương chuyển động
(xem hình 2). Sau khi vượt qua dải nhám ván có vận tốc v
= 3m/s. Lấy g = 10m/s2. Tính hệ số ma sát trượt giữa ván
trượt với dải đường nhám.
Bài 4: Một ống hình trụ thẳng đứng có thể tích V. Ở phía dưới pít tông khối lượng m, diện tích S,
có một lượng khí lý tưởng đơn nguyên tử ở nhiệt độ T0. Pít tông ở vị trí cân bằng chia ống thành
hai nửa bằng nhau. Người ta đun nóng khí từ từ đến khi nhiệt độ khí là 4T0. Ở phía trên có làm hai
vấu để pít tông không bật ra khỏi ống.Hỏi khí trong ống đã nhận được một nhiệt lượng là bao
nhiêu? Bỏ qua bề dày pít tông và ma sát giữa pít tông và thành ống. Cho áp suất khí quyển bên
ngoài là P0 và nội năng của một mol khí lý tưởng đơng nguyên tử được tính theo công thức
3
2
U RT
..............Hết..................
Hình 1
m
R
0
v
Hình 2
l
N
KỲ THI CHỌN HỌC SINH GIỎI TỈNH THPT NĂM 2011
HƯỚNG DẪN CHẤM MÔN VẬT LÝ LỚP 10
Bài Đáp án Điểm
Bài 1
5 điểm
1) 3.0 điểm
- Bảo toàn cơ năng với gốc thế năng ở VTCB:
mgL - mgL(1-cos
) =
2
2
mv
2 cos
v gL
=
10 3 4,16 /
m s
- Áp dụng định luật II Niu tơn:
T-mgcos
=
2
cos 2 cos 3 cos 13
mv m
T mg gl mg N
l l
- Gia tốc tiếp tuyến : at =gsin
= 5m/s2
- Gia tốc pháp tuyến:
2
2
2 cos 10 3 /
n
v
a g m s
l
- Gia tốc toàn phần:
2 2 2
18 /
t n
a a a m s
- Hướng của
:
a a
tạo với bán kính nối vật với tâm 0 một góc
với
tan 0, 29
t
n
a
a
2) 2.0 điểm
- Gọi v1 là vận tốc quả cầu ở vị trí cao nhất của quỹ đạo tròn tâm I,bán
kính R,ta có
mgl(1- cos
)
- mg2R =
22
11
2 (1 os ) 4
2
mv
v gl c gR
(1)
- Điều kiện để quả cầu quay được quanh I trong mặt phẳng thẳng đứng là:
T =
2
1
0
mv mg
R
(2)
- Từ (1) và (2) suy ra : cos
5
1 0,25
2
R
l
0
75,5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
Bài 2
5 điểm
1) 2.0 điểm
- áp dụng định lý động năng:
Vận tốc tại M: 2
2 (1 os )
v gR c
(1)
- Định luật II Niu tơn :
mgcos
2
mv
N
R
(2)
- Từ (1) và (2) suy ra : N =mg(3cos
-2)
- vật bắt đầu trượt khi N = 0
2
os
3
c
0.5
0.5
0.5
0.5
P
x
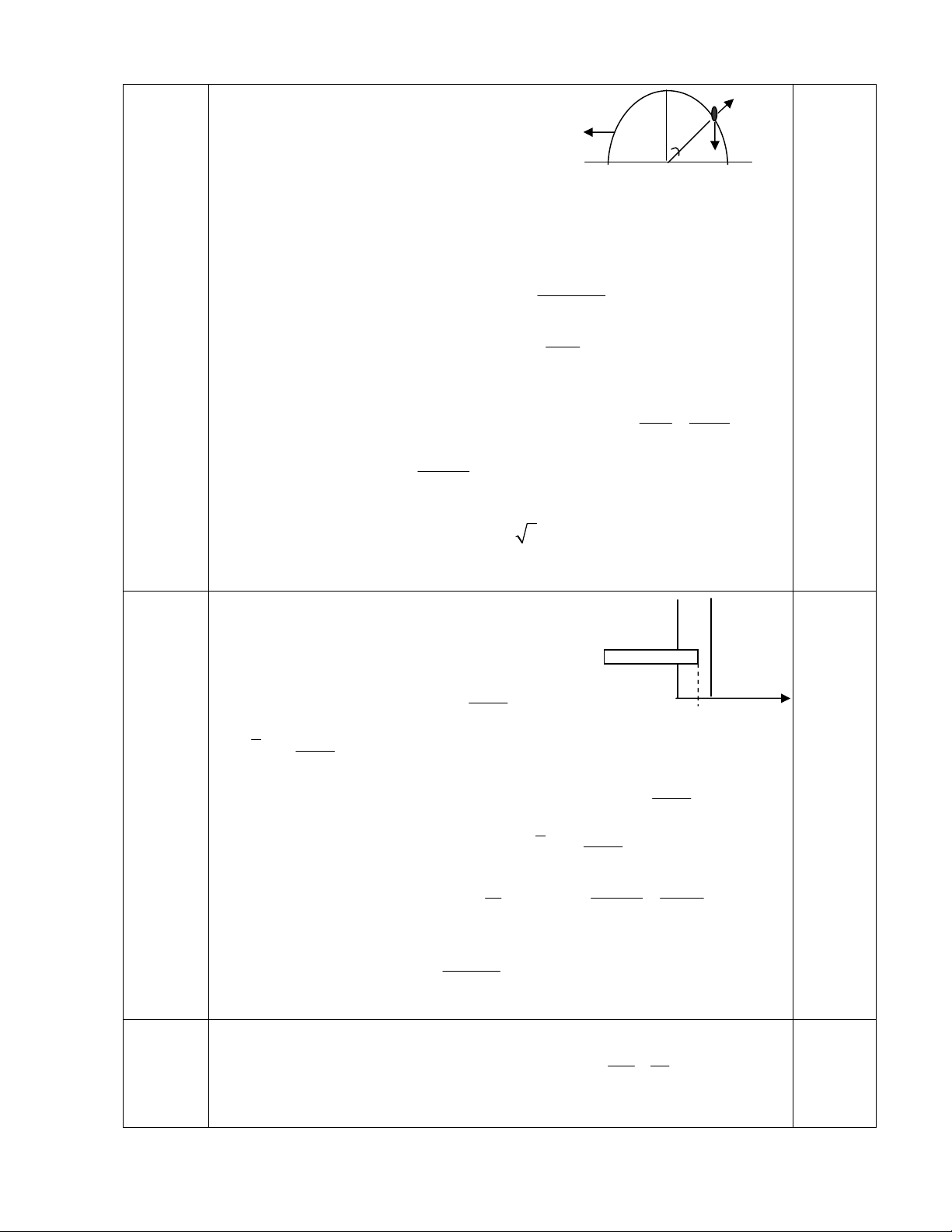
2) 3.0 điểm M m
V
- Gọi
V
là vận tốc bán cầu,
u
là vận tốc của
M so với bán cầu. Vận tốc của m so với đất là :
v u V
- Theo phương ngang động lượng bảo oàn nên :
cos
( cos )
x
mu
mv MV m u V MV V
M m
(1)
- Khi m bắt đầu rời khỏi M thì :
2
cos
mu
mg
R
2
cos (2)
u gR
- Mặt khác ; 2 2 2
2 cos
v V u uV
(3)
- Ap dụng định luật bảo toàn cơ năng :
2 2
(1 os )
2 2
mv MV
mgR c
(4)
- Từ (1),(2),(3),(4) suy ra: 3
os 3cos 2 0
mc
M m
- Với M=m ,ta có : 3
os 6cos 4
c o
- Giải phương trình này ta được cos
=
3 1
0.5
0.5
0.5
0.5
0.5
0.5
Bài 3
5
điểm
- Chọ hệ tọa độ 0x như hình
- Khi đầu tấm ván có tọa độ : 0
x l
,lực ma sát
tác dụng lên xe có độ lớn: Fms1 =
mg
x
L
1
2
ms
mg
F l
L
- Khi
l x L
: lực ma sát không đổi và có độ lớn 2ms
mg
F l
L
- Khi đuôi của ván có tọa độ : 0
x l
: 3ms
F
2
mg
l
L
- áp dụng định lý đông năng,ta có :
2
2 2
0
( ) ( )
2
m mgl mgl
v v L l
L L
-
2 2
0
0,4
2
v v
gl
1.0
1.0
1.0
1.0
1.0
- Khi pít tông ở VTCB, Các thông số khí : P1= P0 +
mg
s
;
0
2
V
; T0
P
0
x
Bài 4
5 điểm
Số mol khí 1 0
1 1
1 0
2
PV
PV
n mol
RT RT
- Trong giai đoạn đầu,pít tông chưa chạm vấu khí biến đổi đẳng áp, khi bắt
đầu chạm vấu khí có nhiệt độ T2
Áp dung: 1 2
2 0 0
1 2
2
2
V V V
T T T
T T V
- Nhiệt lượng truyền cho khí trong quá trình này :
1 1
1 1 2 1 0
0
3 3
( )
2 2 2 2 2
PV PVV
Q A U P n R T T RT
RT
=
1
5
4
PV
- Sau khi pít tông chạm vấu, thể tích không đổi,dây là quá trình đẳng tích
Khí nhận nhiệt lượng chỉ làm tăng n
ội năng:
1
2 0 0 1
0
3 3 3
2 2
2 2 2 2
PV
Q n R T R T PV
RT
Tổng nhiệt lượng mà khí đã nhận :
1 2 1 0
11 11
( )
4 4
mg
Q Q Q PV P V
s
1.0
1.0
1.0
1.0
1.0