CHƯƠNG III:ĐỊNH GIÁ DOANH
CHƯƠNG
III:ĐỊNH
GIÁ
DOANH
NGHIỆP VÀ THẨM ĐỊNH DỰ ÁN
Ầ Ư
Đ
Ầ
U T
Ư
Nội Dung Chương III
Giá trị thời gian của tiền tệ
Định giá dòng tiền
Định
giá
dòng
tiền
Định giá trái phiếu
Đị h
iá
ổ
hiế
Đị
n
h
g
iá
c
ổ
phiế
u
Các tiểuchuẩnđánh giá dựán đầutư
Quyếtđịnh đầutưvốn
Phân tích và đánh
g
iá d
ự
án
g
ự
Giá TrịThờiGianCủaTiềnTệ
Tiềntê có gia trịtheo thời gian:Mộtđồng chúng
ta nhậnđược hôm nay có gia trịhơnmộtđồng
chúng ta nhậnđư
ợ
c trong tương lai
b
ở
i vì:
•Tiềnđem đầutưphảisinhlợi
ắ
ắ
•Tương lai là không ch
ắ
cch
ắ
nnênmộtđộng
trong tương lai sẽkhác mộtđồng trong hiệntại
Ti
ề
ê
bị
ấ
ứ
đi
ề
ki
ệ
l
•
Ti
ề
nt
ê
bị
m
ấ
ts
ứ
c mua trong
đi
ề
u
ki
ệ
n
l
ạm
phát
Giá TrịThờiGianCủaTiềnTệ
Giá trịtương lai củamộtkhoảntiền
•Giá tr
ị
tươn
g
lai
(
future value
)
:là
g
iá tr
ị
củam
ộ
tkhoảnđầu
ị
g
(
)
g
ị
ộ
tưsau một hay nhiềukỳđầutư.
•Lái suất kép (compound interest) là lãi suấtthuđượctừviệc
đầ
kh ả
iề
ố
b
đầ
à
lãi
ấ
ái
đầ
đầ
utư
kh
o
ả
nt
iề
ng
ố
c
b
an
đầ
uv
à
lãi
su
ấ
tt
ái
đầ
utư.
•Lãi của lãi (interest on interest) là lãi suấtthuđượctừviệctái
đầu
tư
các
khoản
lãi
trước
đây
đầu
tư
các
khoản
lãi
trước
đây
.
•Lãi suấtđơn (simple interest) là lãi suấtthuđượctừkhoản
tiềngốcđầutưban đầu.
•Lũykế(compounding): là quá trình lũykếlãi suấtcủamột
khoảnđầutưtheo thờigianđêcóthêmlãisuất
Giá TrịThờiGianCủaTiềnTệ
Giá trịtương lai củamộtkhoảntiền
Ví dụ 1: Chúng ta đầutư100 USD vớilãisuất 10% mộtnăm trong 5
ề
ầ
năm. Gia
s
ư
ti
ề
nlãiđượctáiđ
ầ
ut
ư
:
Sô tiềnnhậnđượctrongcácnăm:
Nă
1
100
+
100
*
10
%
100
*(
1
+
10
%)
110
$
•
Nă
m
1
:
100
+
100
*
10
%
=
100
*(
1
+
10
%)
=
110
$
•Năm2:100*(1+10%)+100*(1+10%)*10%=100*(1+10%)^2=121$
•
Năm
3
:
•
Năm
3
:
100*(1+10%)^2+100*(1+10%)^2*10%=100(1+10%)^3=133,1$
•
N
ăm 4: 100
(
1+10%
)
^4=146
,
41
(
)
,
•Năm 5: 100(1+10%)^5=161,05
Giá TrịThờiGianCủaTiềnTệ
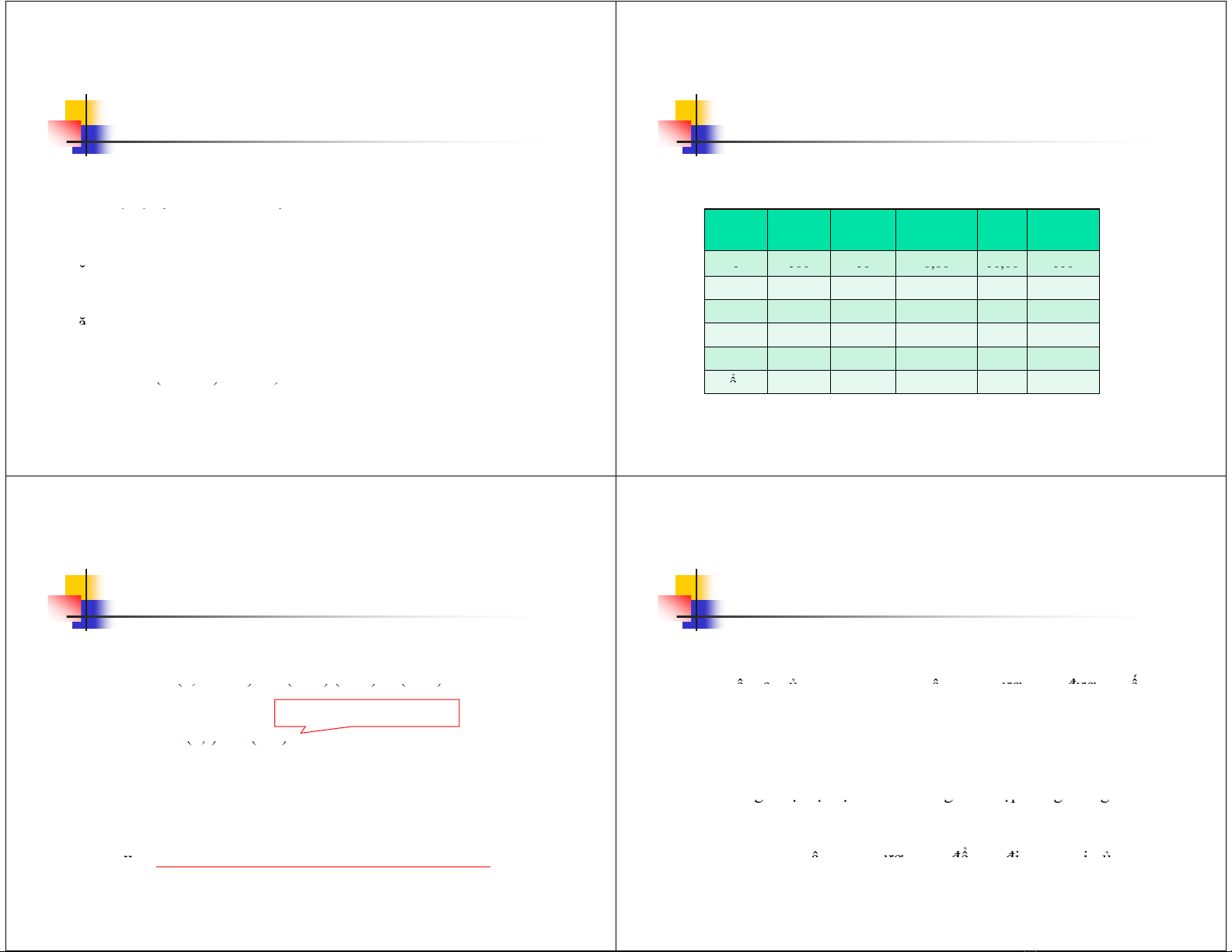
Giá trịtương lai của khoảnđầutư100 USD, lãi suất 10%, trong 5 năm
NămGiátrị
đầukỳ
Lãi đơnLãicủalãi Lãi
kép
Giá trị
cuốikỳ
1
100
10
0,00
10,00
110
1
100
10
0,00
10,00
110
2 110 10 1,00 11,00 121
3 121 10 2,10 12,10 133,10
4 133,1 10 3,31 13,10 146,41
5 146,41 10 4,64 14,64 16105
Tổng
50
11 05
61 05
Tổng
50
11
,
05
61
,
05
Giá TrịThờiGianCủaTiềnTệ
Giá trịtương lai củamộtkhoảntiền
FV
(
n
,
r
1
r
2
r
n
)
=PV
(
1+r
1
)
(
1+r
2
)
…
(
1+r
n
)
(,
1
,
2
…
n
)(
1
)(
2
)(
n
)
Nếur
1=r2=rn
FV(
n,r
)
=
PV(1
+
r)
n
Thừasốlũykế
FV(
n,r
)PV(1r)
FV: Gia trị tương lai củamột khoảntiền
n: Sô năm
r: Lãi suấtnăm(%)
PV: Gia trị hiệntại
Ví
dụ
2
:
\
\
Spreedsheet
\
gia
tri
tien
te
cua
thoi
gian xls
Ví
dụ
2
:
..
\
..
\
Spreedsheet
\
gia
tri
tien
te
cua
thoi
gian
.
xls
Giá TrịThờiGianCủaTiềnTệ
Giá trịhiệntạicủamộtkhoảntiền:
•Giá trịhiệntại (present value) : là giá trịtạithờiđiểm
hiện
tại
của
các
dòng
thu
nhập
trong
tương
lai
được
chiết
hiện
tại
của
các
dòng
thu
nhập
trong
tương
lai
được
chiết
khấuvớitỉlệchiếtkhấu phù hợp
•Chiếtkhấu (discount) là việc tính toán giá trịhiệntạicủa
các khoản thu nhập trong tương lai
•Lãi suấtchiếtkhấu (discount rate) là lãi suất dùng để
tính
g
iá tr
ị
hi
ệ
nt
ạ
icủa các dòn
g
thu nh
ập
tron
g
tươn
g
lai.
g
ị
ệ
ạ
g
ập
g
g
•Định giá bằng dòng tiềnchiếtkhấu (discounted cash
flow valuation) là việc tính toán giá trịhiệntạicủamột
dòng
thu
nhập
trong
tương
lai
để
xác
định
giá
trị
của
nó
dòng
thu
nhập
trong
tương
lai
để
xác
định
giá
trị
của
nó
vào ngày hôm nay.
Giá TrịThờiGianCủaTiềnTệ
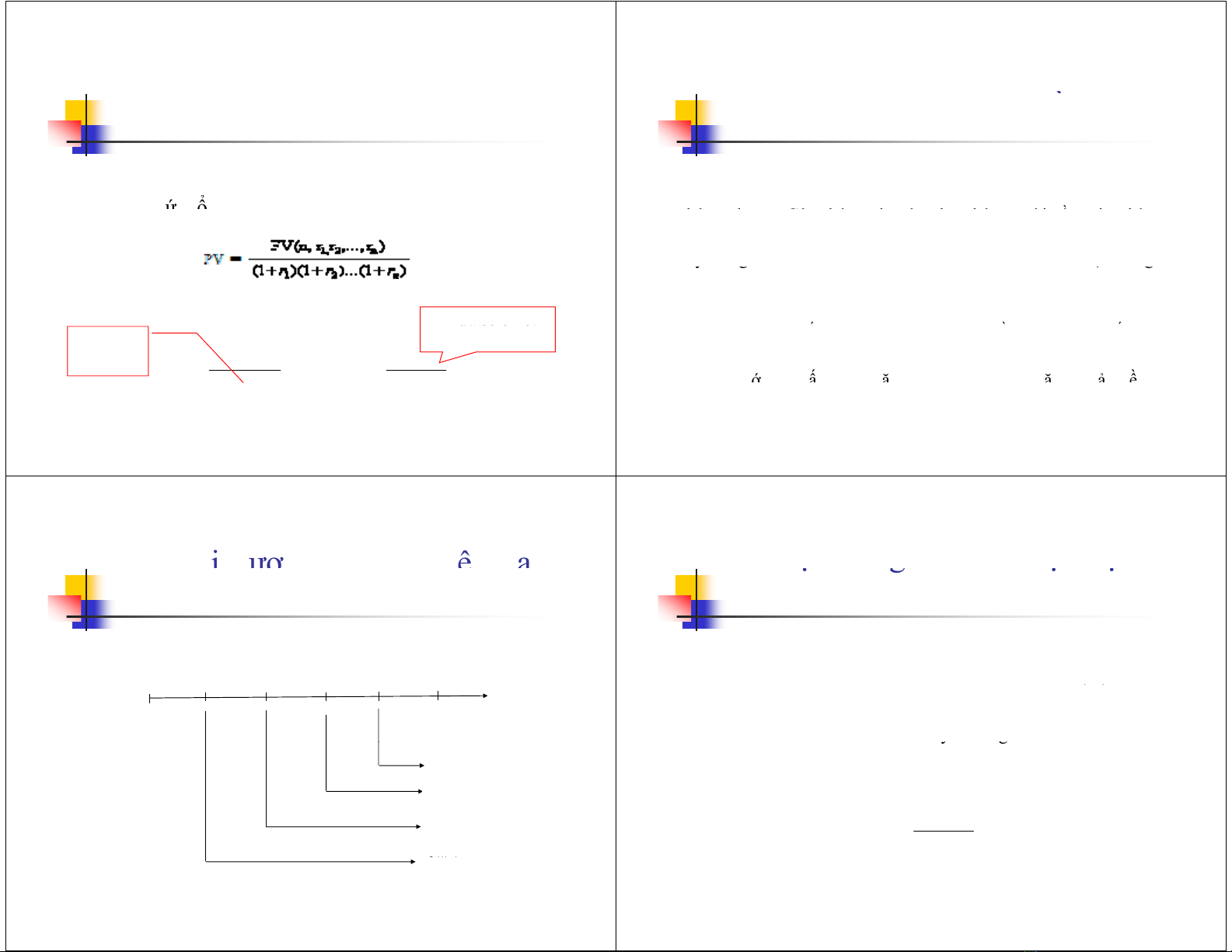
Giá trịhiệntạicủamột khoảntiền trong tương lai
•
Công
thức
tổng
quát
:
•
Công
thức
tổng
quát
:
Nếur
1=r2=rn
Thừa
số
chiết
nn
r
rnFV
r
rnFV
PV
)
1
(
1
),(
)
1
(
),(
+
×=
+
=
Thừa
số
chiết
khấu
Lãi suất
chiếtkhấu
r
r
)
1
(
)
1
(
+
+
ề
Giá TrịThờiGianCủaTi
ề
nTệ
Ví dụ3: Năm 1995, công ty ABC cầnvaymột khoản1tỷUSD
trong 25 năm. Để vay khoảntiềnnày,côngtyđã phát hành các
hứ
h
Cá
hứ
h
à
h
hé
ời
ầ
i
hậ
c
hứ
ng c
h
ỉnợ.
Cá
cc
hứ
ng c
h
ỉn
à
yc
h
o
phé
pngư
ời
c
ầ
mg
iữ
n
hậ
n
được $1000 sau 25 năm. Nếulàbạn, bạnsẽmua chứng chỉnợ
nà
y
với
g
iá bao nhiê
u
n
ế
ubi
ế
tlãisu
ấ
tchi
ế
tkh
ấ
utrênth
ị
trườn
g
y
g
ị
g
là 8%?
Ví dụ4: Một nhà đầutưcó khoảnđầutưban đầu là $100. Hỏi
ấ
ề
ấ
a) Vớilãisu
ấ
t là bao nhiêu thì khoảnti
ề
nnàysẽtăng g
ấ
p
đôi sau 8 năm?
b)
Với
lãi
suất
là
8%/
năm
thì
sau
bao
nhiêu
năm
khoản
tiền
b)
Với
lãi
suất
là
8%/
năm
thì
sau
bao
nhiêu
năm
khoản
tiền
này sẽtăng gấpđôi?
Giá
Trị
Tương
Lai
Và
Hiện
Tại
Giá
Trị
Tương
Lai
Và
Hiện
Tại
Của Dòng Tiên
Giá trịtương lai củamộtdòngtiền(FVA)bằng tổng giá trị
tương lai của các khoản thu nhập thành phần.
2
n
3
1
2
n
01
3
n-
1
c1c2c3
Cn*(1+r)0
Cn-1 cn
(1+r)(n-3)
C3*(1+r)(n-3)
(1+r)1
Cn-1*(1+r)1
C
*(
1)
(
1)
(1+r)(n-1)
C2*(1+r)(n-2)
(1+r)(n-2)
C
1
*(
1
+r
)
(
n-
1)
Giá Tr
ị
Tươn
g
Lai Và Hi
ệ
nT
ạ
i
ị
g
ệ
ạ
Của Dòng Tiền
Công thứctổng quát
FVA(
nr
)
=
C
(1+r)
0
+
C
(1+r)
1
+
C
(1+r)
2
+
C
(1+r
)
(
n-1
)
FVA(
n
,
r
)
C
n
(1+r)
+
C
n-1
(1+r)
+
C
n-2
(1+r)
+
….
C
1
(1+r
)
(
)
Nế
uC
0
= C
1
==
C
n
đâ
y
là dòn
g
ti
ề
nđ
ề
uvà
0
1
…
n
,
y
g
FVA(n,r)=C[(1+r)0 + (1+r)1+(1+r)2+…..+(1+r)(n-1)]
⎥
⎦
⎥
⎢
⎣
⎢−+
=r
r
CrnFVA
n1)1(
).(
G
i
á
Tr
ị
T
ươ
n
g
L
a
i
Và
Hi
ệ
nT
ạ
i
Của
Giá
Trị
Tương
Lai
Và
Hiện
Tại
Của
Dòng Tiền
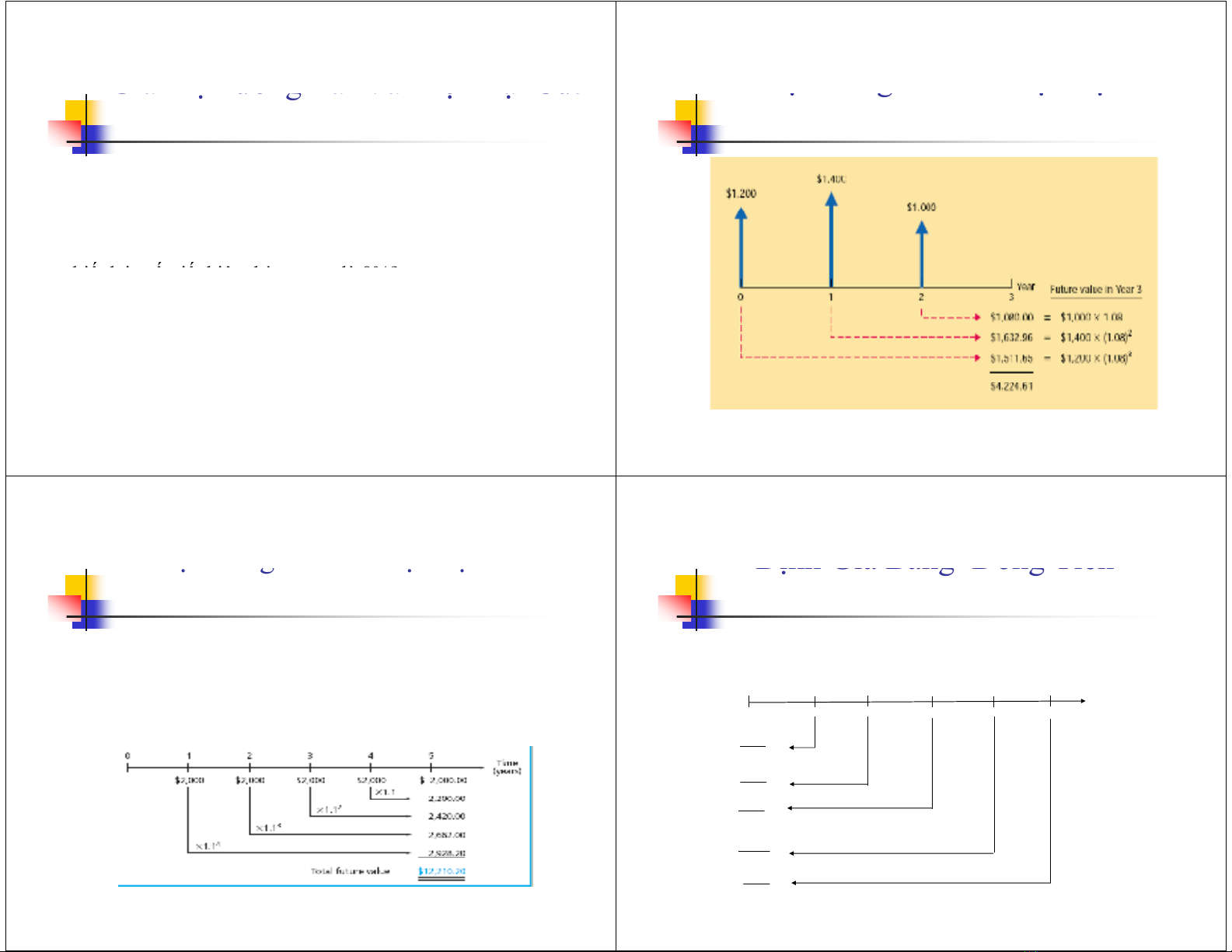
Ví dụ5: Một sinh viên hiệntại có $1200 trong tài
khoản, sau 1 nămanhta
b
ỏthêm $1400 vào tài khoản
vàsau2nămanhtalạibỏtiếp $1000 vào tài khoản. Hỏi
sau 3 nămanhtasẽcó bao nhiêu tiền trong tài khoản
biế
li
ấ
iế
kiệ
hà
là
8
%
?
biế
t
l
ã
i
su
ấ
tt
iế
t
kiệ
m
hà
ng năm
là
8
%
?
.
Giá Tr
ị
Tươn
g
Lai Và Hi
ệ
nT
ạ
i
ị
g
ệ
ạ
Của Dòng Tiền
G
iá Tr
ị
Tươn
g
Lai
V
àHi
ệ
nT
ạ
i
C
ủa
G
ị
g
V
ệ
ạ
C
Dòng Tiền
Ví dụ6: Mộtnhàđầutưquyếtđịnh gửitiếtkiệmmột
khoảntiền là 2.000 USD vào cuốinăm trong vòng 5
năm. Nếulãisuấttiếtkiệm là 10% thì sau 5 năm nhà
đầutưcó bao nhiêu tiền?
Định
Giá
Bằng
Dòng
Tiền
Định
Giá
Bằng
Dòng
Tiền
ChiếtKhấu
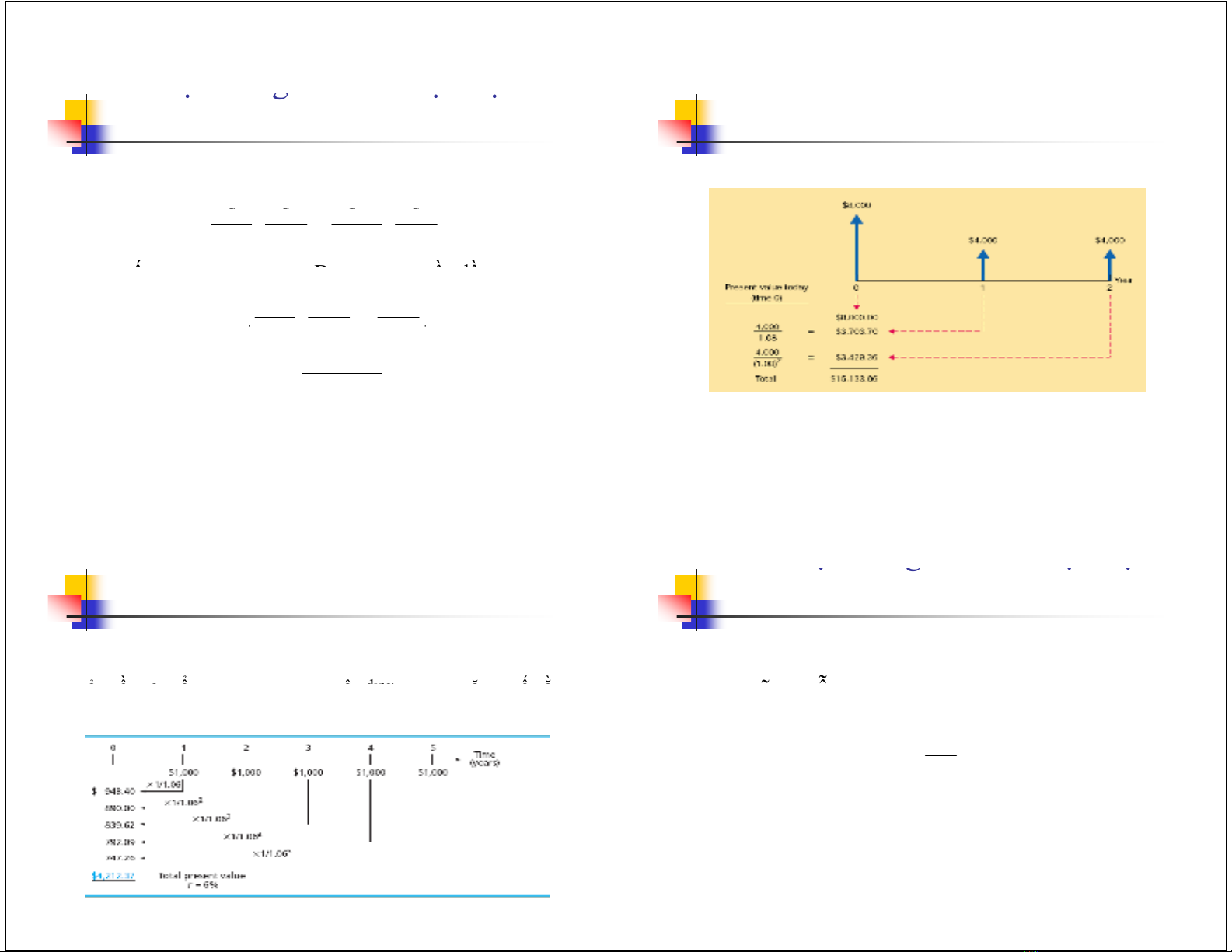
Giá trịhiệntạicủa dòng tiền(PVA) bằng tổng giá trịhiệntạicủa
các khoản thu nhập trong tương lai
12 3n-1
n
C1C2C3Cn-1 Cn
0
1
C
1
1
)1( r
C
+
2
2
)1( r
C
+
3
3
)1( r
C
+
1
1
)
1
(
−
−
+
n
n
r
C
)
1
(
+
r
n
n
r
C
)1( +
Giá Tr
ị
Tươn
g
Lai Và Hi
ệ
nT
ạ
i
ị
g
ệ
ạ
Của Dòng Tiền
C
C
C
C
Công thứctổng quát:
n
n
n
n
r
C
r
C
r
C
r
C
rnPVA )1()1(
...
)1()1(
),( 1
1
2
2
1
1
+
+
+
+
+
+
+
=−
−
Nế
C
C
C
Æ
Đâ
là
dò
tiề
đề
à
⎥
⎦
⎤
⎢
⎣
⎡++
=
n
C
rn
P
VA
)
1
(
1
....
)
1
(
1
)
1
(
1
)
,
(
2
1
Nế
u
C
1=
C
2=…
C
n
Æ
Đâ
y
là
dò
ng
tiề
n
đề
uv
à
:
⎥
⎦
⎢
⎣
+++
n
rrr
)
1
(
)
1
(
)
1
(
)
(
2
1
}
)1/(1[1
{),(
r
r
CrnPVA
n
+−
=
r
Giá TrịTương Lai Và HiệnTại
Của Dòng Tiền
Để so sánh 2 phương thức thanh toán ta phải quy đổi giá trảgóp vềhiệntại
Vậyvớimứclãisuất8%/nămbạn nên chọnphương thức thanh toán trảgóp
Giá TrịTương Lai Và HiệnTại
Của Dòng Tiền
Ví dụ:Giảsửsinh viên A trong vòng 5 năm,mỗinămnhậnđược
1000 USD tiềnhọcbổng vào cuốinăm. Hãy tính giá trịhiệntạicủa
khoản
tiền
học
bổng
mà
sinh
viên
A
nhận
được
trong
5
năm
biết
rằng
khoản
tiền
học
bổng
mà
sinh
viên
A
nhận
được
trong
5
năm
,
biết
rằng
lãi suấtchiếtkhấulà6%/năm.
Giá Tr
ị
Tươn
g
Lai Và Hi
ệ
nT
ạ
i
ị
g
ệ
ạ
Của Dòng Tiền
Giá trịhiệntạicủamột niên kim-dòng tiềnđềuvà
ké
dài
ĩh
iễ
ké
o
dài
v
ĩ
n
h
v
iễ
n
C
r
C
PV
=


























