F
E
D C
BA
EF
C
D
A
Chuyên đề 5 (6tiết):
ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC, CỦA HÌNH THANG
*) Kiến thức cơ bản :
1. a) Đường thẳng đi qua trung điểm một cạnh của tam giác và
song song với cạnh thứ hai thì nó đi qua trung điểm của cạnh thứ ba.
b) Đường thẳng đi qua trung điểm một cạnh bên của hình thang
và song song với hai đáy thì đi qua trung điểm của cạnh bên thứ hai.
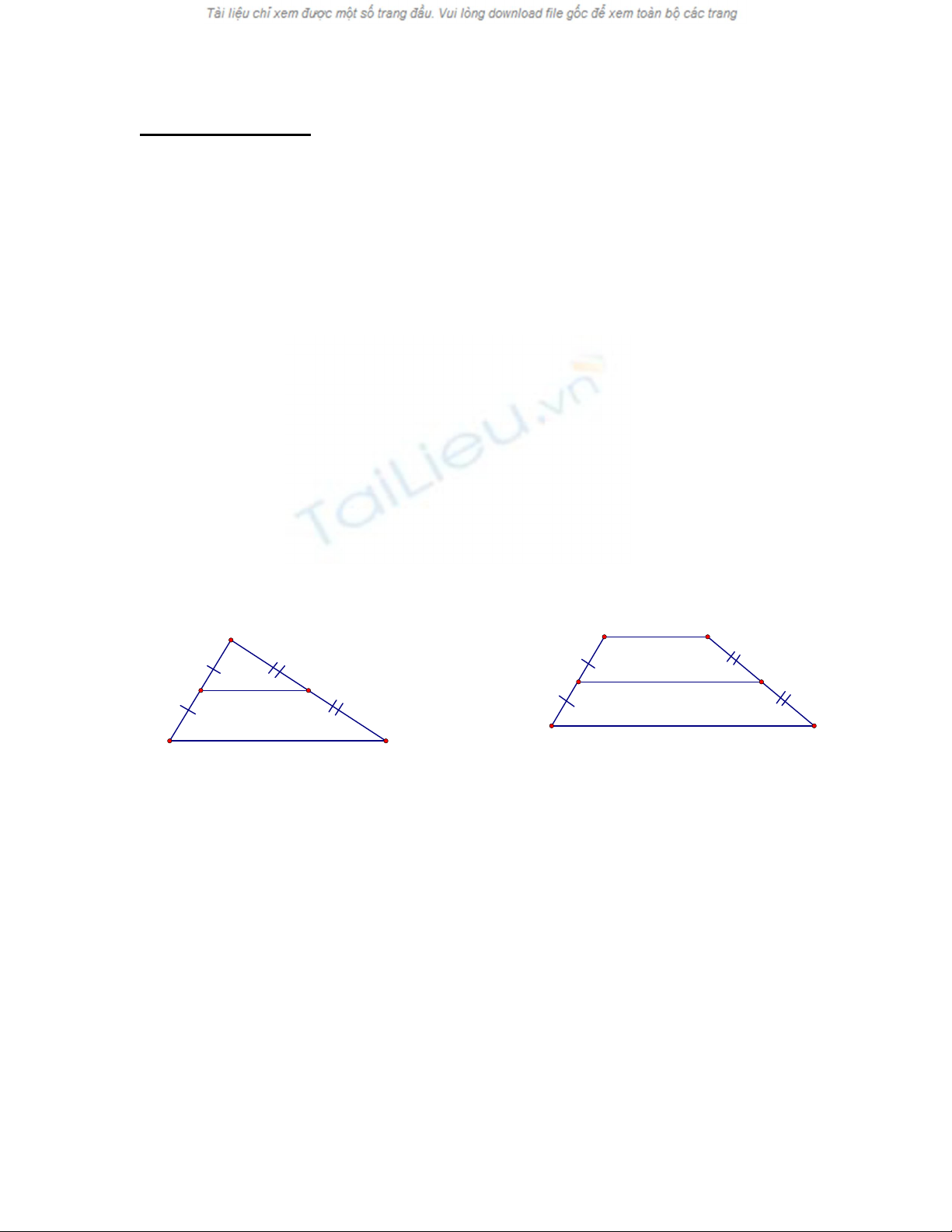
2. a) Đường trung bình của tam giác là đoạn thẳng nối trung điểm
hai cạnh của tam giác. (h.8)
b) Đường trung bình của hình thang là đoạn nối trung điểm hai
cạnh bên của
hình thang.(h.9)
h.8 h.9

NM
D C
BA
3.a) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng
nửa cạnh đấy.
b) Đường trung bình của hình thang thì song song với hai đáy
và bằng nửa tổng hai đáy.
Bổ sung :
Trong hình thang có hai cạnh bên không song song, đoạn thẳng
nối trung điểm hai đường chéo thì song song với hai đáy và
bằng nửa hiệu hai đáy.
Trong h.10 :
MN // AB // CD
CD AB
MN
2
.
CÁC VÍ DỤ MINH HỌA
*) Ví dụ 1:
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD và BC.
Chứng minh rằng nếu
AB CD
MN
2
thì tứ giác ABCD là hình thang.
ON
M
DC
B
A
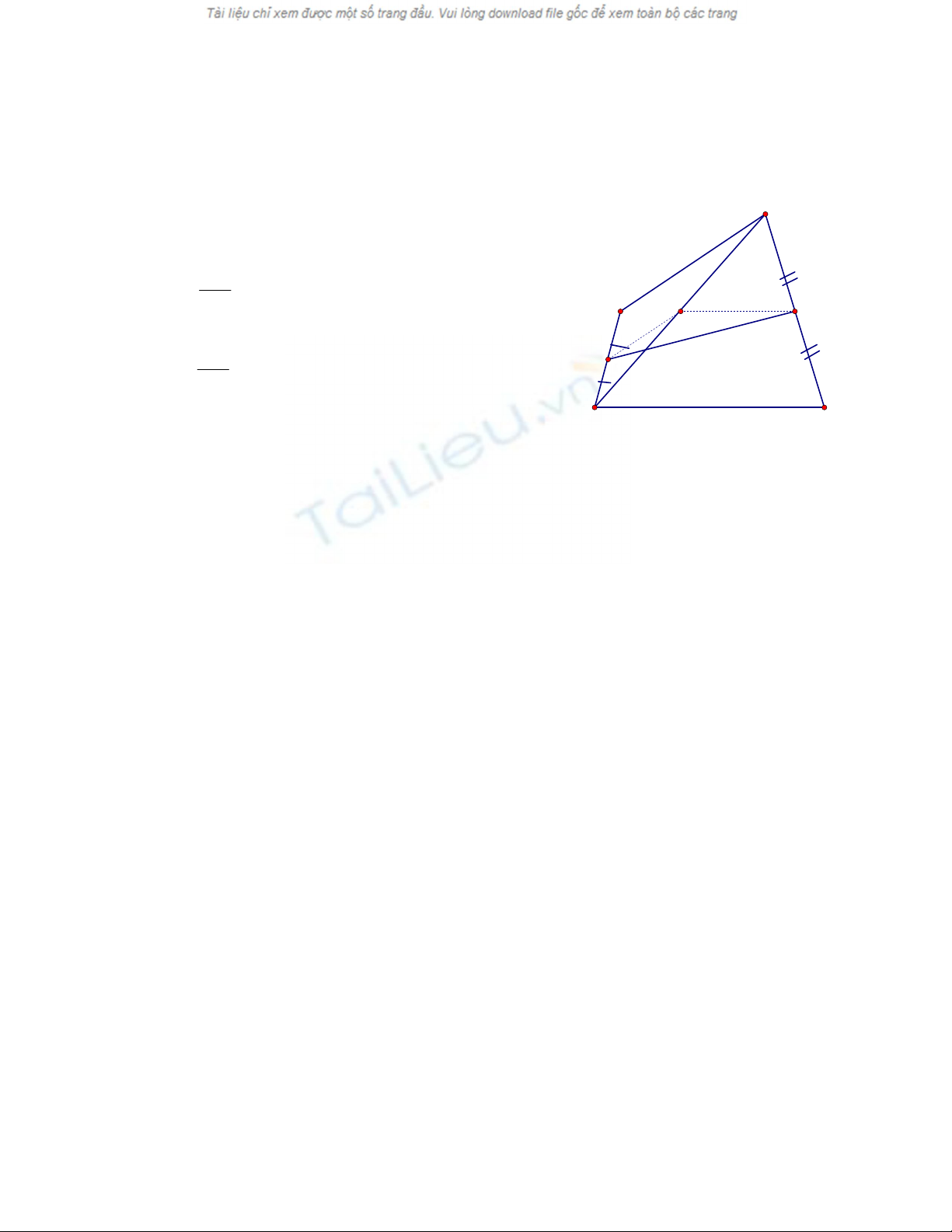
Giải :
Gọi O là trung điểm của BD. Các đoạn thẳng OM, ON lần lượt là
đường trung bình của
ABD
và
BCD
nên
AB
OM
2
và OM // AB ; (1)
ON =
CD
2
và ON // CD ; (2)
Suy ra O nằm giữa M và N. Vậy ba điểm
M, O, N thẳng hàng (3).
Từ (1), (2), (3) suy ra AB // CD do đó tứ giác ABCD là hình thang.
+) Nhận xét :
Trong giả thiết của bài toán có trung điểm hai cạnh đối của tứ giác,
nối hai điểm này ta chưa được đường trung bình của tam giác nào cả. Vì thế
ta đã vẽ thêm trung điểm của đường chéo BD ( hoặc AC ) và vận dụng được
định lí đường trung bình của tam giác để chứng minh.
Việc vẽ thêm trung điểm của một đoạn thẳng để vận dụng đường
trung bình của tam giác là việc vẽ đường phụ thường gặp khi giải bài toán
hình học.
*) Ví dụ 2 :
PQN
M
D C
BA
Cho hình thang ABCD ( đáy AB nhỏ hơn đáy CD ). Tìm điều kiện
của hình thang này để hai đường chéo của nó chia đường trung bình thành
ba phần bằng nhau.
Giải :
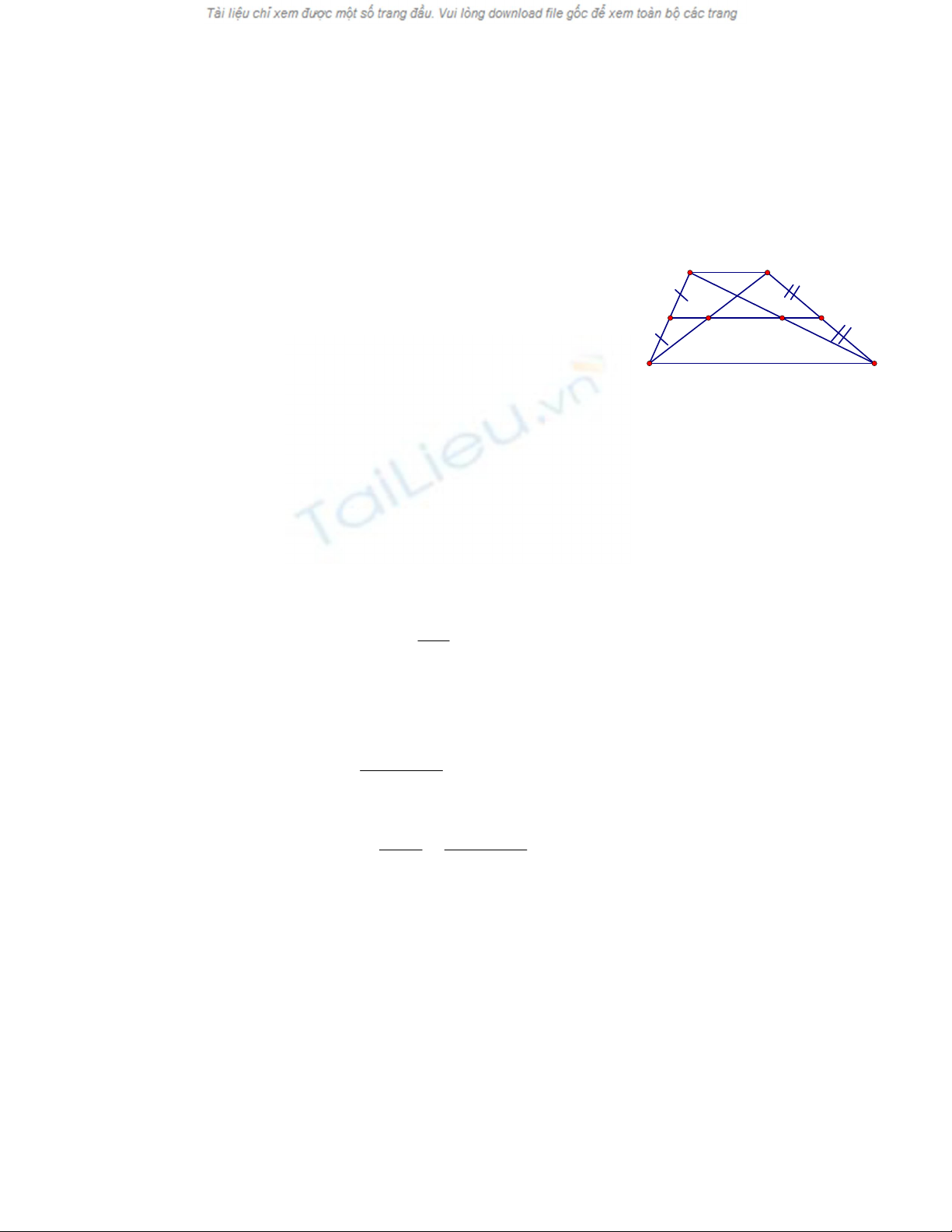
Gọi M, N lần lượt là trung điểm của AD và BC ;
MN cắt BD tại P, cắt AC tại Q ; MN là đường trung
bình của hình thang nên MN // AB // CD.
Xét
ABD
có MA = MD ; MP // AB nên PB = PD
Xét
ADC
có MA = MD ; MQ // CD nên QA = QC.
MP và NQ lần lượt là đường trung bình của
ABD
và
ABC
nên
AB
MP NQ
2
.
PQ là đoạn nối trung điểm hai đường chéo của hình thang ABCD nên
CD AB
PQ
2
.
Ta có : MP = +Q = QN
AB2 CD AB
2 2
AB CD AB
CD 2.AB
+) Nhận xét :

FO
D
M
B
H N I G PK
C
E
A
Nếu không có điều kiện đáy AB nhỏ hơn đáy CD thì khi AB = 2.CD ,
chứng minh tương tự như trên ta vẫn có hai đường chéo chia đường trung
bình thành ba phần bằng nhau.
Tóm lại, nếu hình thang có một đáy gấp đôi đáy kia thì hai đường chéo của
nó chia đường trung bình làm ba phần bằng nhau.
*) Ví dụ 3 :
Từ ba đỉnh của một tam giác, hạ các đường vuông góc xuống một
đường thẳng d không cắt cạnh nào của tam giác đó. Chứng minh rằng tổng
độ dài ba đường vuông góc đó gấp ba lần độ dài đoạn thẳng vuông góc hạ từ
trọng tâm tam giác xuống đường thẳng d.
Giải :
Giả sử
ABC
có ba đường trung tuyến AD, BE, CF cắt nhau tại O;
các đoạn thẳng AG, BH, OI, CK đều vuông góc với đường thẳng d. Ta phải
chứng minh: AG + BH + CK = 3OI


























