www.MATHVN.com
GIÁO ÁN
HÌNH HỌC LỚP 8
Biên soạn theo chương trình chuẩn

www.MATHVN.com
TUẦN I
Chương I : TỨ GIÁC
Tiết 1: §1. Tứ giác
*****
I/ MỤC TIÊU :
HS nắm vững các định nghĩa về tứ giác, tứ giác lồi, tổng các góc của tứ giác lồi.
HS biết vẽ, biết gọi tên các yếu tố, biết tính số đo các góc của một tứ giác lồi. Biết
vận dụng các kiến thức trong bài vào các tình huống thực tiển đơn giản.
Suy luận ra được tổng bốn góc ngoài của tứ giác bằng 360o.
II/ CHUẨN BỊ :
- GV : Compa, eke, thước thẳng, bảng phụ vẽ hình sẳn (H1, H5 sgk)
- HS : Ôn định lí “tổng số đo các góc trong tam giác”.
III/ PHƯƠNG PHÁP:
Đàm thoại, qui nạp, hoạt động nhóm.
III/ HOẠT ĐỘNG DẠY- HỌC :
NỘI DUNG HOẠT ĐỘNG CỦA GV
HOẠT ĐỘNG CỦA HS
Hoạt động 1 : Kiểm ra (5’)
Kiểm tra đ
ồ dùng học tập
của HS, nhắc nhở HS ch
ưa có
đủ …
HS cùng bàn ki
ểm tra lẫn
nhau và báo cáo…
Hoạt động 2 : Giới thiệu bài mới (1’)
§1. TỨ GIÁC Gi
ới thiệu tổng quát kiến
thức lớp 8, chương I, bài mới
HS nghe và ghi tên
chương, bài vào vở.
Hoạt động 3 : Định nghĩa (20’)
1.Định nghĩa:
A
B
D
C
+Tứ giác ABCD
là hình
gồm 4 đoạn thẳng
AB, BC,
CD, DA, trong đó b
ất kỳ 2
đoạn thẳng nào cũng
không
cùng nằm trên 1 đư
ờng
thẳng
T
ứ giác ABCD (hay ADCB,
BCDA, …)
Treo hình 1,2 (sgk) : Mỗi
hình trên đều gồm 4 đoạn
thẳng AB, BA, CD, DA.
Hình nào có hai đoạn thẳng
cùng thuộc một đư
ờng thẳng?
Các hình 1a,b,c đều được
gọi là tứ giác, hình 2 không
được gọi là tứ giác. Vậy theo
em, thế nào là tứ giác ?
GV chốt lại (định nghĩa nh
ư
SGK) và ghi bảng
GV giải thích rõ nội dung
định nghĩa bốn đoạn thẳng
liên tiếp, khép kín, không
cùng trên một đường thẳng
Giới thiệu các yếu tố, cách
gọi tên tứ giác.
HS quan sát và trả lời
(Hình 2 có hai đoạn thẳng
BC và CD cùng nằm trên
một đoạn thẳng)
HS suy nghĩ – trả lời
HS1: (trả lời)…
HS2: (trả lời)…
HS nh
ắc lại (vài lần) và ghi
vào vở
HS chú ý nghe và quan sát
hình vẽ để khắc sâu kiến
thức
Vẽ hình và ghi chú vào vở
www.MATHVN.com
Các đỉnh: A, B, C, D
Các c
ạnh: AB, BC, CD,
DA.
+Tứ giác lồi là tứ giác
luôn
nằm trong 1 n
ửa mặt phẳng
có bờ là đư
ờng thẳng chứa
bất kỳ cạnh nào của t
ứ giác
?2
A
B
D C
M
P
N
Q
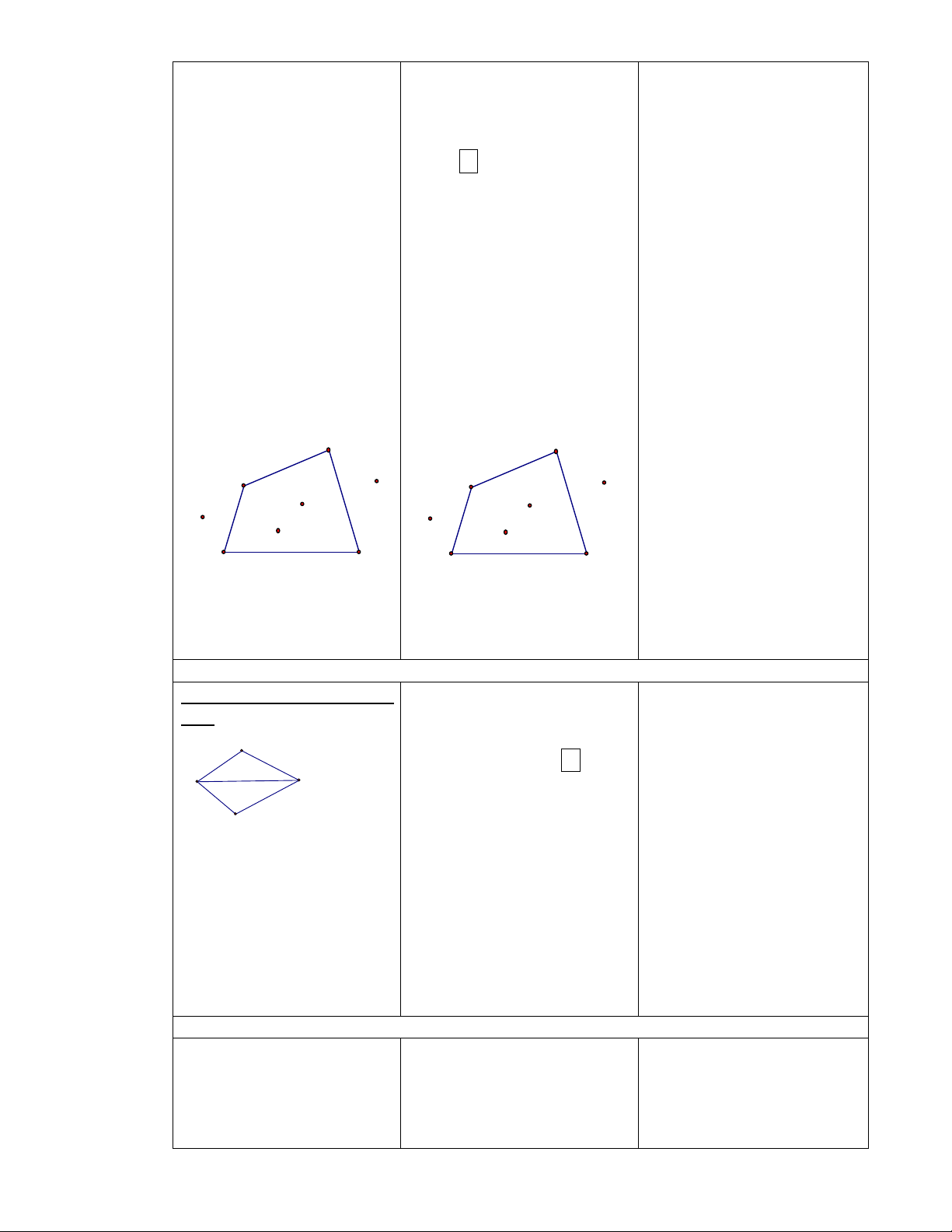
Thực hiện ?1 : đặt mép
thước kẻ lên mỗi cạnh của tứ
giác ở hình a, b, c rồi y/c HS
trả lời ?1
GV chốt lại vấn đề và nêu
định nghĩa tứ giác lồi
GV nêu và giải thích chú ý
(sgk)
Treo bảng phụ hình 3. yêu
cầu HS chia nhóm làm ?2
GV quan sát nhắc nhở HS
không tập trung
Đại diện nhóm trình bày
A
B
D C
M
P
N
Q
Trả lời: hình a
HS nghe hiểu và nhắc lại
định nghĩa tứ giác lồi
HS nghe hiểu
HS chia 4 nhóm làm trên
bảng phụ
Thời gian 5’
a)* Đỉnh kề: A và B, B và
C, C và D, D và A
* Đỉnh đối nhau: B và D,
A và C
b) Đường chéo: BD, AC
c) Cạnh kề: AB và BC, BC
và CD,CD và DA, DA và
AB
d) Góc: A, B, C, D
Góc đối nhau: A và C, B và
D
e) Điểm nằm trong: M, P
Điểm nằm ngoài: N, Q
Hoạt động 4 : Tồng các góc của một tứ giác (7’)
2. Tồng các góc của một tứ
giác
1
2
2
1
A
B
D
C
Kẻ đường chéo AC, ta có :
A1 + B + C1 = 180o,
A2 + D + C2 = 180o
(A1+A2)+B+(C1+C2)+D =
360o
vậy A + B + C + D = 360o
Định lí : (Sgk)
Vẽ tứ giác ABCD :Dự đoán
xem tổng số đo bốn góc của
tứ giác bằng bao nhiêu?
Cho HS thực hiện ?3 theo
nhóm nhỏ
Theo dõi, giúp các nhóm
làm bài
Cho đại diện vài nhóm báo
cáo
GV chốt lại vấn đề (nêu
phương hướng và cách làm,
rồi trình bày cụ thể)
HS suy ngh
ĩ (không cần trả
lời ngay)
HS thảo luận nhóm
theo
yêu cầu của GV
Đ
ại diện một vài nhóm nêu
rõ cách làm và cho bi
ết kết
qu
ả, còn lại nhận xét bổ
sung, góp ý …
HS theo dõi ghi chép
Nêu kết luận (đ
ịnh lí) , HS
khác lặp lại vài lần.
Hoạt động 5 : Củng cố (7’)
Bài 1 trang 66 Sgk
a) x=500 (hình 5)
b) x=900
c) x=1150
d) x=750
Treo tranh vẽ 6 tứ giác nh
ư
hình 5, 6 (sgk) y/c HS nh
ẩm
tính
và trả lời kết quả.
HS tính nhẩm số đo góc x
a) x=500 (hình 5)
b) x=900
c) x=1150
d) x=750
www.MATHVN.com
a) x=1000 (hình 6)
a) x=360 a) x=1000 (hình 6)
a) x=360
Hoạt động 6 : Dặn dò (5’)
BTVN.
Bài tập 2 trang 66 Sgk
Bài tập 3 trang 67 Sgk
Bài tập 4 trang 67 Sgk
Bài tập 5 trang 67 Sgk
Học bài: Nắm sự khác nhau
giữa tứ giác và tứ giác lồi; tự
chứng minh định lí tồng các
góc trong tứ giác
Bài tập 2 trang 66 Sgk
! Sử dụng tổng các góc 1 tứ
giác
Bài tập 3 trang 67 Sgk
! Tương tự bài 2
Bài tập 4 trang 67 Sgk
! Sử dụng cách vẽ tam giác
Bài tập 5 trang 67 Sgk
! Sử dụng toạ độ để tìm
HS nghe dặn và ghi chú
vào vở
Tiết 2: §2. Hình thang
*****
I/ MỤC TIÊU :
HS nắm được định nghiã hình thang, hình thang vuông, các yếu tố của hình thang. Biết
cách chứng minh một tứ giác là hình thang, là hình thang vuông.
HS biết vẽ hình thang, hình thang vuông; tính số đo các góc của hình thang, hình thang
vuông. Biết sử dụng dụng cụ để kiểm tra một tứ giác là hình thang.
Biết linh hoạt khi nhận dạng hình thang ở những vị trí khác nhau và ở các dạng đặc
biệt (hai cạnh song song, hai đáy bằng nhau)
II/ CHUẨN BỊ :
GV : Thước thẳng, êke, bảng phụ ( ghi câu hỏi ktra, vẽ sẳn hình 13), phấn màu
HS : Học và làm bài ở nhà; vở ghi, sgk, thước, êke…
III/ PHƯƠNG PHÁP:
Đàm thoại, qui nạp, hợp tác nhóm
IV/ HOẠT ĐỘNG DẠY- HỌC :
NỘI DUNG HOẠT ĐỘNG CỦA GV HOẠT ĐỘNG CỦA HS
Hoạt động 1 : Kiểm ra bài cũ (8’)
Đ
ịnh nghĩa tứ giác
ABCD?
Đlí v
ề tổng các góc cuả
một tứ giác?
Cho tứ giác ABCD,biết
ˆ
A
= 65o,
ˆ
B
= 117o,
ˆ
C
= 71o
+ Tính góc D?
+ Số đo góc ngoài tại D?
Treo bảng phụ ghi câu hỏi
kiểm tra; gọi một HS lên
bảng.
Kiểm tra vở btvn vài HS
Thu 2 bài làm của HS
Đánh giá, cho điểm
Chốt lại các nội dung chính
Một HS lên bảng trả lời và
làm bài lên b
ảng. Cả lớp làm
bài vào vở .
117
75
65
B
D
C
A
ˆ
D
= 36006501170710=
1070
Góc ngoài tại D bằng 730
Nhận xét bài làm ở bảng .
www.MATHVN.com
(định nghĩa,
đlí, cách tính góc
ngoài)
HS nghe và ghi nhớ
Hoạt động 2 : Giới thiệu bài mới (1’)
§2. HÌNH THANG
Chúng ta đã biết về tứ giác
và tính chất chung của nó. Từ
tiết học này, chúng ta sẽ
nghiên cứu về các tứ giác đặc
biệt với những tính chất của
nó. Tứ giác đầu tiên là hình
thang.
HS nghe giới thiệu
Ghi tựa bài vào vở
Hoạt động 3 : Hình thành định nghĩa (18’)
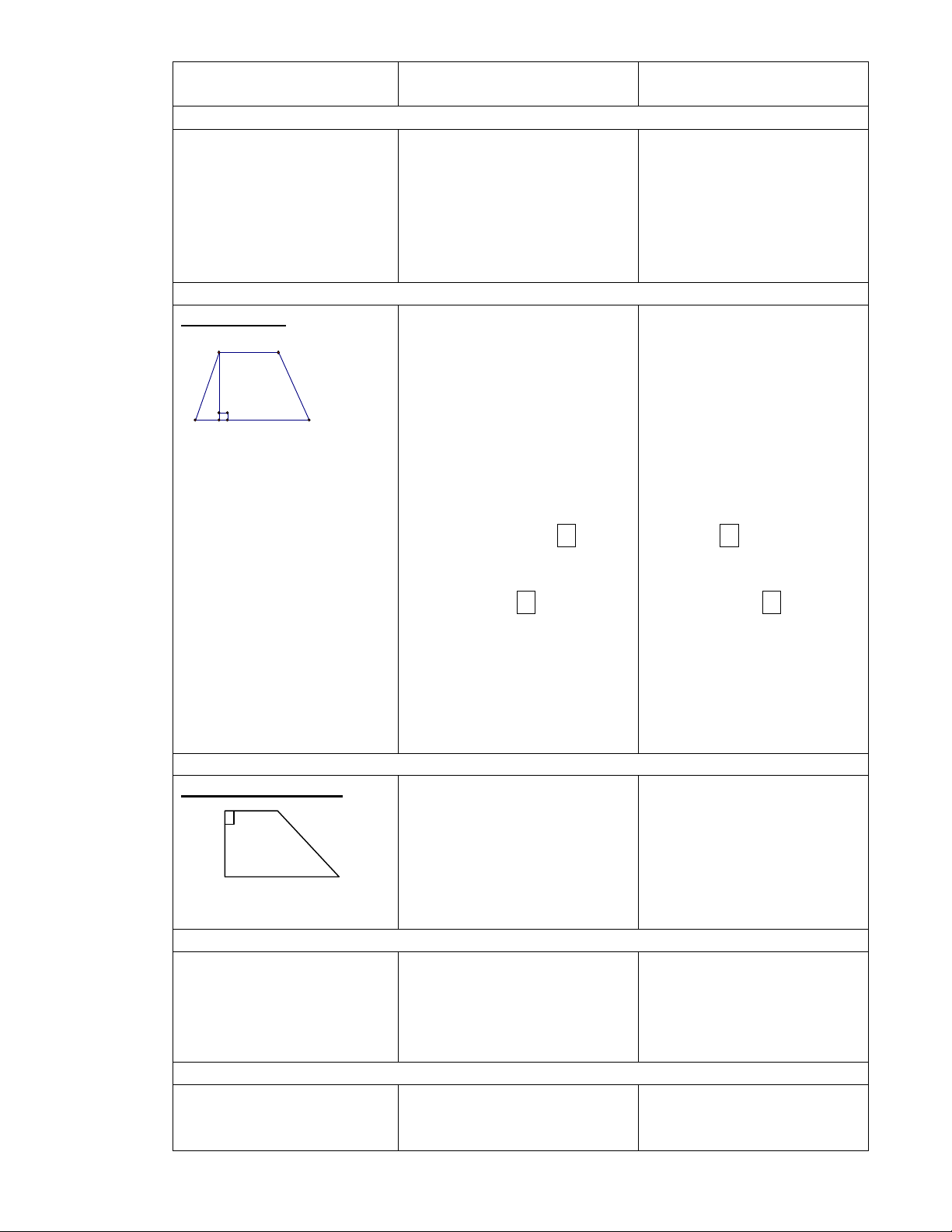
1.Định nghĩa: (Sgk)
H
AB
D C
Hình thang ABCD
(AB//CD)
AB, CD : cạnh đáy
AD, BC : cạnh bên
AH : đường cao
* Hai góc k
ề một cạnh bên
của hình thang thì bù nhau.
* Nhận xét: (sgk trang 70)
Treo bảng phụ vẽ hình 13:
Hai cạnh đối AB và CD có gì
đặc biệt?
Ta gọi tứ giác này là hình
thang. Vậy hình thang là hình
như thế nào?
GV nêu lại định nghiã hình
thang và tên gọi các cạnh.
Treo bảng phụ vẽ hình 15,
cho HS làm bài tập ?1
Nhận xét chung và chốt lại
vđề
Cho HS làm ?2 (vẽ sẳn các
hình 16, 17 sgk)
Cho HS nhận xét ở bảng
Từ b.tập trên hãy nêu kết
luận?
GV chốt lại và ghi bảng
HS quan sát hình , nêu
nhận xét AB//CD
HS nêu định nghĩa hình
thang
HS nh
ắc lại, vẽ hình và ghi
vào vở
HS làm ?1 t
ại chỗ từng câu
HS khác nhận xét bổ sung
Ghi nhận xét vào vở
HS thực hiện ?2 trên phiếu
học tập hai HS làm ở bảng
HS khác nhận xét bài
HS nêu kết luận
HS ghi bài
Hoạt động 4: Hình thang vuông (8’)
2.Hình thang vuông:
A B
D C
Hình thang vuông là hình
thang có 1 goc vuông
Cho HS quan sát hình 18, tính
D
ˆ?
Nói: ABCD là hình thang
vuông. Vậy thế nào là hình
thang vuông?
HS quan sát hình – tính
D
ˆ
D
ˆ= 900
HS nêu định nghĩa hình
thang vuông, vẽ hình vào vở
Hoạt động 5: Củng cố (5’)
Bài 7 trang 71
a) x = 100o ; y = 140o
b) x = 70o ; y = 50o
c) x = 90o ; y = 115o
Treo bảng phụ hình vẽ 21
(Sgk)
Gọi HS trả lời tại chỗ từng
trường hợp
HS kiểm tra bằng trực
quan, bằng ê ke và trả lời
HS trả lời miệng tại chỗ
bài tập 7
Hoạt động 6: Dặn dò (5’)
Bài tập 6 trang 70 Sgk
Học bài: thuộc định nghĩa
hình thang, hình thang
vuông.
HS nghe dặn và ghi chú


























