B¸o c¸o tèt nghiÖp Lª M¹nh Hïng
Líp tù ®éng ho¸ 46 Khoa c¬ ®iÖn – Tr−êng DHNNI - HN
12
víi phÐp tÝnh And, t−¬ng øng biÕn lu«n cã gi¸ trÞ 0 lµ phÇn tö ®¬n vÞ cña phÐp tÝnh
Or. Nªn ta cã:
x^1 = 1^x = x. Víi mäi x thuéc B.
xV 0 = 0Vx = x. Víi mäi x thuéc B.
§Þnh nghÜa: Kh«ng giíi h¹n quy ®Þnh cña b¶ng ch©n lý vÒ c¸c phÐp tÝnh And,
Or, Not nÕu trªn (B) ta x¸c ®Þnh ®−îc 3 phÐp tÝnh And, Or, Not tho¶ m·n.
1) xVy = yVx.
2) xV(y^z) = (xVy)^z.
3) (x^y)V(xVy) = x.
Mäi x, y, z thuéc B th× tËp B cïng 3 phÐp tÝnh ®ã sÏ ®−îc gäi lµ ®¹i sè Boole.
2.TÝnh chÊt:
Mét ®¹i sè Boole B víi 3 phÐp tÝnh And, Or, Not cã c¸c tÝnh chÊt sau:
TÝnh chÊt 1:
X
= X.
B
X
∈
∀.
TÝnh chÊt 2: X = X.X = X^X.
B
X
∈
∀
.
TÝnh chÊt 3:
X
.X = 0.
B
X
∈
∀
.
TÝnh chÊt 4:1VX = 1.
B
X
∈
∀.
TÝnh chÊt 5: 0VX = X.
TÝnh chÊt 6:
X
VX = 1.
TÝnh chÊt 7: X.Y = yxx +
1.2.4. C¸c phÇn tö l«gic c¬ b¶n.
Trong kÜ thuËt sè còng nh− trong viÖc ®iÒu khiÓn b»ng PLC th× ng−êi ta
th−êng dïng c¸c phÐp tÝnh c¬ b¶n lµ AND (
∧
), OR (∨), NOT , NAND, NOR. Ta
cã c¸c quan hÖ l«gic lµ:
• PhÇn tö AND.
Lµ phÇn tö cã nhiÒu ®Çu vµo vµ mét ®Çu ra, ®Çu ra cã gi¸ trÞ l«gic b»ng 1 khi
tÊt c¶ c¸c ®Çu vµo b»ng 1.
B¸o c¸o tèt nghiÖp Lª M¹nh Hïng
Líp tù ®éng ho¸ 46 Khoa c¬ ®iÖn – Tr−êng DHNNI - HN
13
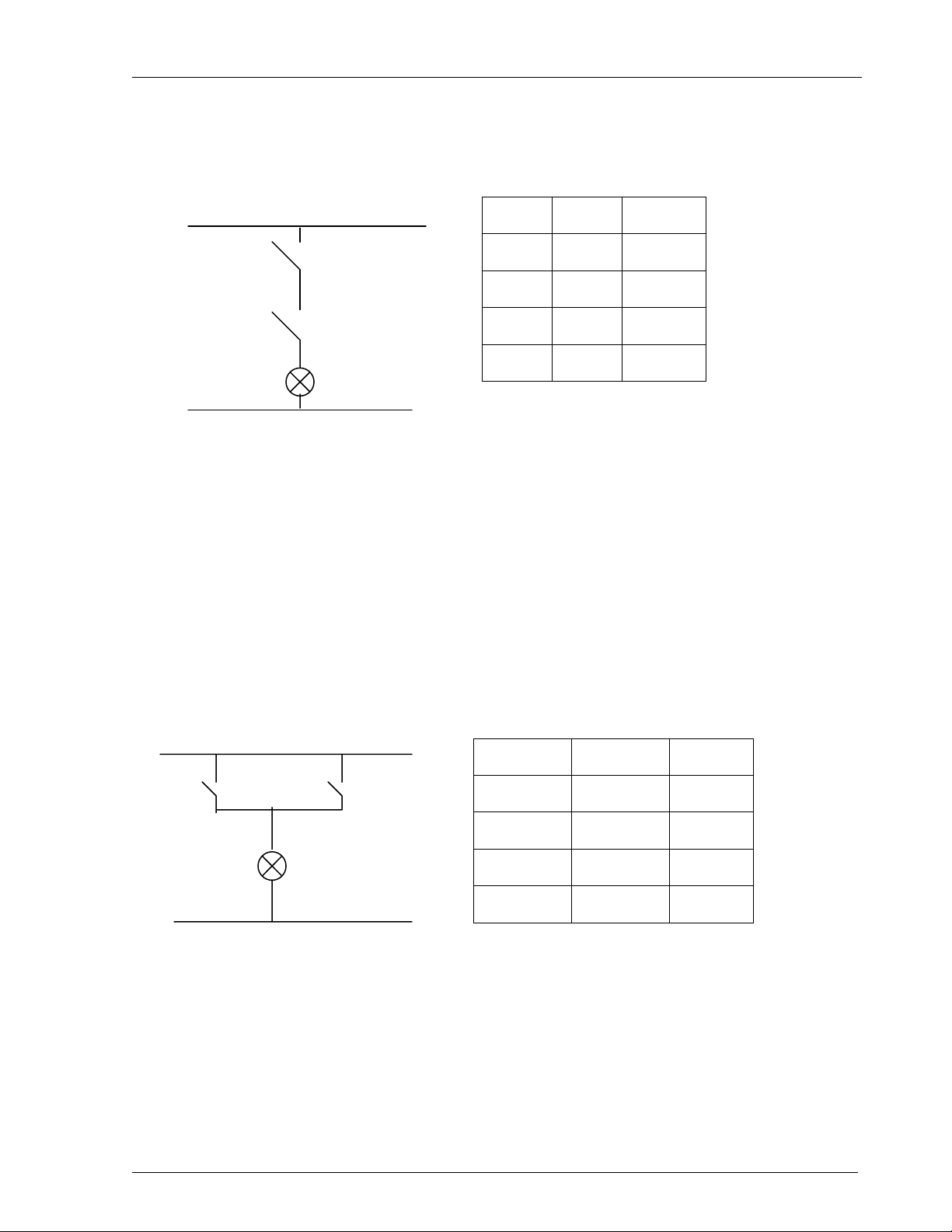
Gi¶ sö xÐt phÇn tö AND hai ®Çu vµo.(KÝ hiÖu hai ®Çu vµo lµ S1 vµ S2, ®Çu ra lµ
H1)
24V
S2
S1
H1
0V
B¶ng ch©n lý
H×nh 1.1: M¹ch ®iÖn l«gic and
VËy NÕu c¶ hai kho¸ S1 vµ S2 ®Òu ®ãng m¹ch th× ®Ìn míi s¸ng. VËy s¬ ®å
®iÖn trªn thÓ hiÖn quan hÖ l«gic AND.
H
1 = S1∧S2
H
1 = S1.S2
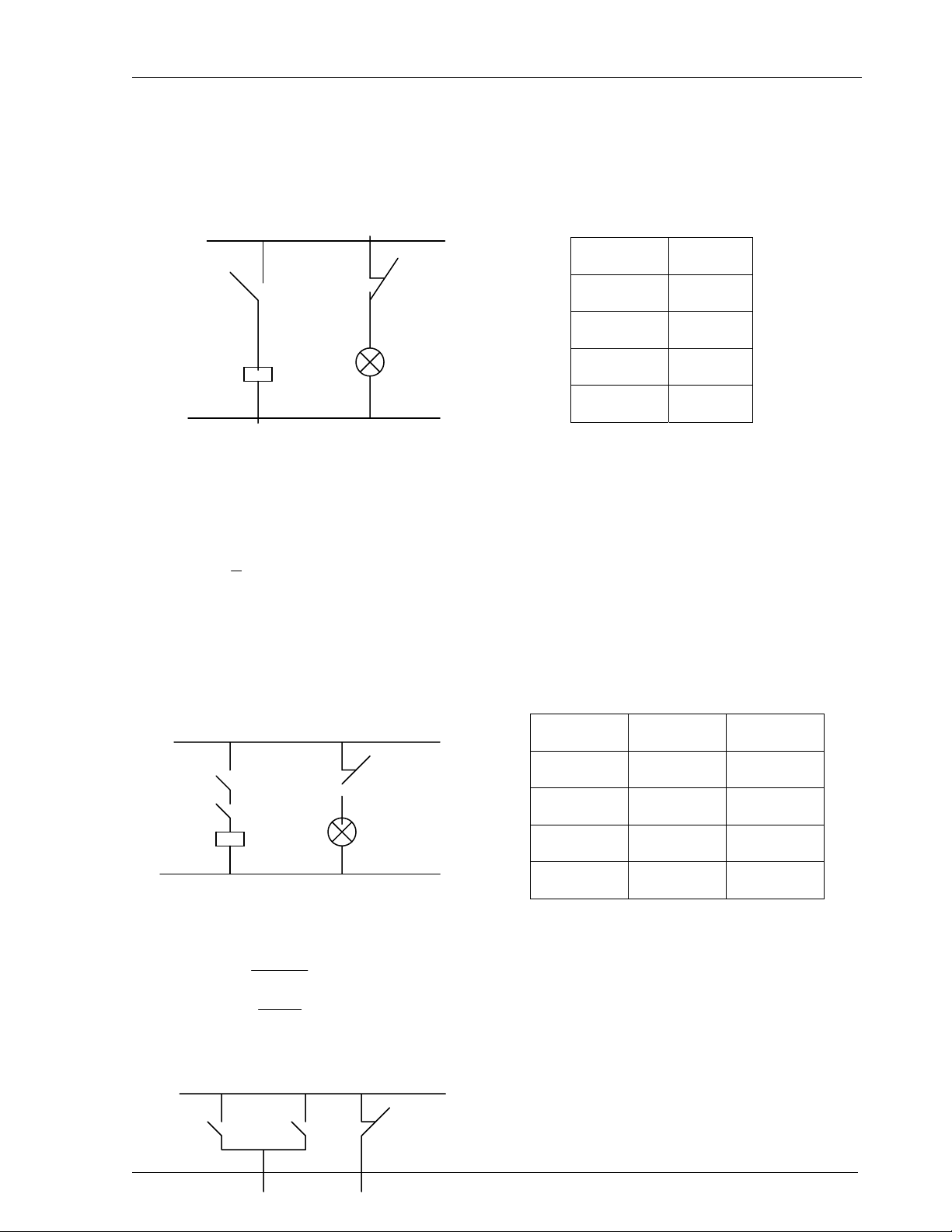
PhÇn tö OR: Lµ phÇn tö cã nhiÒu ®Çu vµo vµ mét ®Çu ra. Cã gi¸ trÞ b»ng 1 khi
Ýt nhÊt mét trong c¸c ®Çu vµo b»ng 1.
24V
S1 S2
H1
0V
B¶ng ch©n lý.
H×nh1.2: M¹ch ®iÖn logic OR
Trong ®ã nÕu S1 hoÆc S2, hoÆc c¶ S1, S2 ®Òu ®ãng th× ®Òu lµm ®Ìn H1 s¸ng nh−
nhau. Sù ®ãng m¹ch cña c«ng t¾c S1, S2 lµm ®Ìn s¸ng lµ quan hÖ l«gÝc OR.
H1= S1+ S2
S1 S
2 H
1
0 0 0
0 1 0
1 0 0
1 1 1
S1 S
2 H1
0 0 0
0 1 1
1 0 1
1 1 1
B¸o c¸o tèt nghiÖp Lª M¹nh Hïng
Líp tù ®éng ho¸ 46 Khoa c¬ ®iÖn – Tr−êng DHNNI - HN
14
H1=S1+ S2
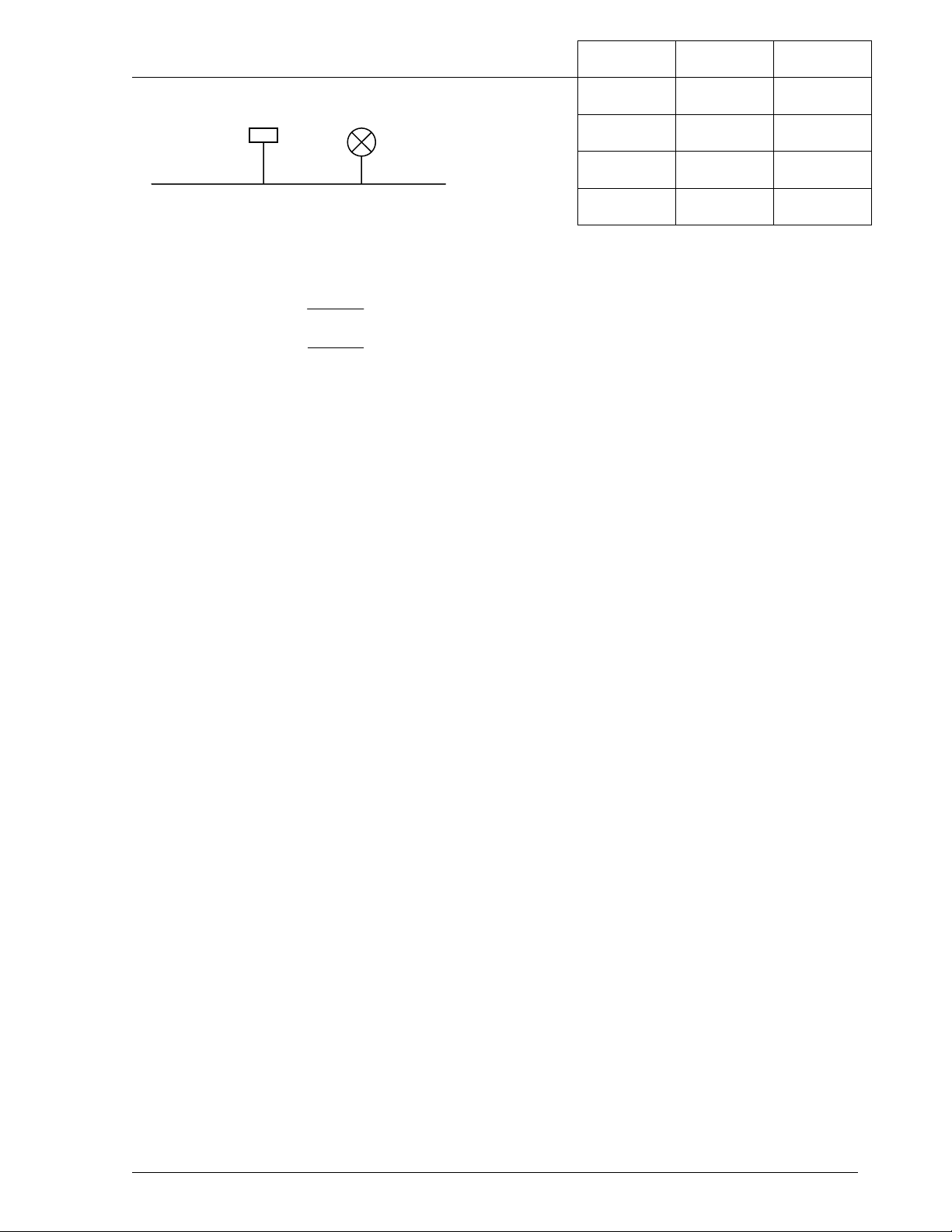
PhÇn tö NOT: Lµ phÇn tö cã 1 ®Çu vµo vµ mét ®Çu ra, tÝn hiÖu ra lµ phñ ®Þnh
tÝn hiÖu vµo.
24V
S1 K1
K1 H1
0V
B¶ng ch©n lý.
H×nh1.3: M¹ch ®iÖn logic NOT
Kho¸ S1 më m¹ch th× ®Ìn s¸ng. Cßn S1 më th× ®Ìn s¸ng.
H1= S1
PhÇn tö NAND vµ phÇn tö NOR: §©y lµ hai phÇn tö AND phñ ®Þnh( AND
Not) vµ OR phñ ®Þnh(OR Not).
24V NAND
S1 K1
S2
K1 H1
0V
H×nh 1.4: M¹ch ®iÖn logic NAND
Ta cã: H1= 21 SS ∧.
H1= 2.1 SS .
NOR
24V
S1 S2 K1
S1 H
1
0 1
0 1
1 0
1 0
S1 S
2 H
1
0 0 1
0 1 1
1 0 1
1 1 0
B¸o c¸o tèt nghiÖp Lª M¹nh Hïng
Líp tù ®éng ho¸ 46 Khoa c¬ ®iÖn – Tr−êng DHNNI - HN
15
K1 H1
0V
B¶ng ch©n lý
H×nh 1.5: M¹ch ®iÖn logic NOR
Ta cã: H1= 21 SS ∨.
H
1= 21 SS +.
1.3. C¸c b−íc thiÕt kÕ hÖ thèng ®iÒu khiÓn l«gic.
ViÖc lËp tr×nh cho c¸c hÖ thèng ®iÒu khiÓn b»ng PLC ngµy cµng ®−îc sö
dông réng r·i. Cã rÊt nhiÒu ph−¬ng ¸n ®Ó thiÕt kÕ, nh−ng ®Ó thuËn tiÖn cho häc viªn
th× ng−êi ta ®· ®−a ra c¸c b−íc chung thiÕt kÕ hÖ thèng ®iÒu khiÓn l«gÝc.
1.3.1. X¸c ®Þnh tÝn hiÖu vµo vµ ra.
B−íc thø hai lµ ph¶i x¸c ®Þnh vÞ trÝ kÕt nèi gi÷a c¸c thiÕt bÞ vµo ra víi PLC.
TÝn hiÖu vµo cã thÓ lµ tiÕp ®iÓm, c¶m biÕn thiÕt bÞ ra cã thÓ lµ r¬le ®iÖn tõ, m«t¬,
®Ìn b¸o. Mçi vÞ trÝ kÕt nèi ®−îc ®¸nh sè t−¬ng tù øng víi PLC sö dông c¸c thiÕt bÞ
vµo/ra cã chøc n¨ng riªng biÖt nhau ta cÇn lùa chän sao cho c¸c bé c¶m biÕn vµ c¸c
bé chÊp hµnh cã thÓ ®−îc nèi trùc tiÕp víi chóng mµ kh«ng cÇn thªm c¸c thiÕt bÞ
phô trî.
1.3.2.ViÕt ph−¬ng tr×nh ®iÒu khiÓn.
C¸c PLC hiÖn cã trªn thÞ tr−êng hÇu hÕt ®ang sö dông 3 c¸ch viÕt th«ng
th−êng ®ã lµ LAD, STL vµ FBD. Tuú theo yªu cÇu cña c«ng nghÖ mµ ta viÕt ch−¬ng
tr×nh ®iÒu khiÓn cho phï hîp.
1.3.3.N¹p ch−¬ng tr×nh vµo bé nhí.
CÊp nguån cho PLC, cµi ®Æt cÊu h×nh khèi giao tiÕp vµo ra nÕu cÇn. Sau ®ã
n¹p ch−¬ng tr×nh so¹n th¶o tõ c¸c thiÕt bÞ lËp tr×nh vµo bé nhí cña PLC. Sau khi
hoµn tÊt nªn kiÓm tra lçi b»ng chøc n¨ng tù chuÈn ®o¸n vµ nÕu cã thÓ th× ch¹y
ch−¬ng tr×nh m« pháng ho¹t ®éng hÖ thèng.
S1 S
2 H
1
0 0 1
0 1 0
1 0 0
1 1 0
B¸o c¸o tèt nghiÖp Lª M¹nh Hïng
Líp tù ®éng ho¸ 46 Khoa c¬ ®iÖn – Tr−êng DHNNI - HN
16
1.3.4.Ch¹y ch−¬ng tr×nh .
Tr−íc khi khëi ®éng hÖ thèng cÇn ph¶i ch¾c ch¾n d©y nèi tõ PLC ®Õn c¸c
thiÕt bi ngo¹i vi lµ ®óng, trong qu¸ tr×nh ch¹y kiÓm tra cã thÓ cÇn thiÕt ph¶i thùc
hiÖn c¸c b−íc tinh chØnh hÖ thèng nh»m ®¶m b¶o an toµn khi ®−a vµo ho¹t ®éng
thùc tÕ.
Tõ c¸c b−íc thiÕt kÕ hÖ thèng trªn ®Ó ®¬n gi¶n vµ dÔ hiÓu, quy tr×nh ®iÒu
khiÓn cã thÓ m« t¶ theo l−u ®å .