KỈ YẾU HỘI NGHỊ SINH VIÊN NGHIÊN CỨU KHOA HỌC NĂM HỌC 2013-2014
7
GIẢI SỐ PHƢƠNG TRÌNH TRUYỀN NHIỆT 2D
Nguyễn Thị Trà My, Lớp K60E, Khoa Toán – Tin
GVHD: TS. Nguyễn Hùng Chính
Tóm tắt: Mô phỏng toán học là một ngành đã và đang phát triển hết sức mạnh mẽ trên thế giới và có
vai trò quan trọng trong hầu hết các lĩnh vực của đời sống xã hội. Cùng với sự phát triển của công
nghệ thông tin nói chung và công nghệ tính toán nói riêng, những mô hình toán học phức tạp (xuất
phát từ các khoa học và thực tiễn) đã được số hóa thành công nghệ và đem lại hiệu quả kinh tế cao.
Báo cáo này trình bày nghiên cứu về phương pháp giải số để giải phương trình truyền nhiệt hai chiều,
một trong những phương trình toán học có nhiều ứng dụng, và đề xuất kĩ thuật đưa thuật toán vào
máy tính để xây dựng chương trình mô phỏng quá trình truyền nhiệt theo thời gian.
Từ khóa: Phương pháp xấp xỉ sai phân, lược đồ tường minh, sự ổn định của lược đồ, phương trình
truyền nhiệt, điều kiện biên Dirichlet.
I. MỞ ĐẦU
Tại sao phải giải số (xấp xỉ nghiệm) của một phƣơng trình toán học? Nhƣ chúng ta
đã biết, phần lớn các mô hình toán học trong thực tế đều không giải đƣợc nghiệm đúng, vì
vậy cần xấp xỉ nghiệm và điều khiển đƣợc sai số của nghiệm gần đúng. Hơn nữa, việc giải
số sẽ đƣa đến thuật toán, tức là ta có thể ra lệnh cho máy tính thực hiện các phép tính để
tìm ra kết quả.
Phƣơng trình truyền nhiệt là một phƣơng trình đạo hàm riêng quan trọng xuất phát từ
mô hình vật lí và có giá trị thực tiễn nhất định. Việc giải phƣơng trình truyền nhiệt cho ta
khảo sát sự phân bố nhiệt lƣợng theo thời gian của một vùng chất điểm, nhƣ một thanh kim
loại (với trƣờng hợp 1 chiều) và mảnh kim loại (với trƣờng hợp 2 chiều).
Phƣơng pháp phổ biến để giải đúng phƣơng trình truyền nhiệt vẫn đƣợc biết đến là
phƣơng pháp Fourier (đƣợc phát triển từ năm 1822 bởi nhà toán học Joseph Fourier). Tuy
nhiên, trong thực hành thí nghiệm, việc cần thay đổi các dữ kiện bài toán, cũng nhƣ việc số
liệu trong thực hành phải tính toán lớn đều làm cho việc giải đúng gặp khó khăn, vì vậy mà
ngƣời ta cần đến phƣơng pháp số để giải phƣơng trình truyền nhiệt.
Phƣơng pháp số là một lĩnh vực của toán học chuyên nghiên cứu các phƣơng pháp
giải gần đúng các bài toán dựa trên những số liệu cụ thể và cho kết quả dƣới dạng số. Với
sự hỗ trợ của máy tính, phƣơng pháp số là công cụ không thể thiếu cho phép thực hiện tính
toán với tốc độ tính toán nhanh và khối lƣợng tính toán lớn.
Báo cáo tập trung vào việc xây dựng phƣơng pháp giải số, thuật toán để giải bài toán
truyền nhiệt, sự ổn định, điều kiện ổn định và đề xuất kĩ thuật số hóa lƣợc đồ, lập chƣơng
trình máy tính và mô phỏng số trong MATLAB.
II. NỘI DUNG
1. Phƣơng pháp số và thuật toán
1.1. Bài toán
Xét phƣơng trình truyền nhiệt trên miền Ω = [a,b]×[c,d] với nguồn nhiệt f(x,y,t) thay
đổi theo thời gian:
KỈ YẾU HỘI NGHỊ SINH VIÊN NGHIÊN CỨU KHOA HỌC NĂM HỌC 2013-2014
8
với là một hằng số dƣơng đặc trƣng cho vận tốc truyền nhiệt.
Giả sử trạng thái ban đầu là:
và điều kiện trên biên xác định bởi:
,
1.2. Giải số (xấp xỉ nghiệm) phương trình
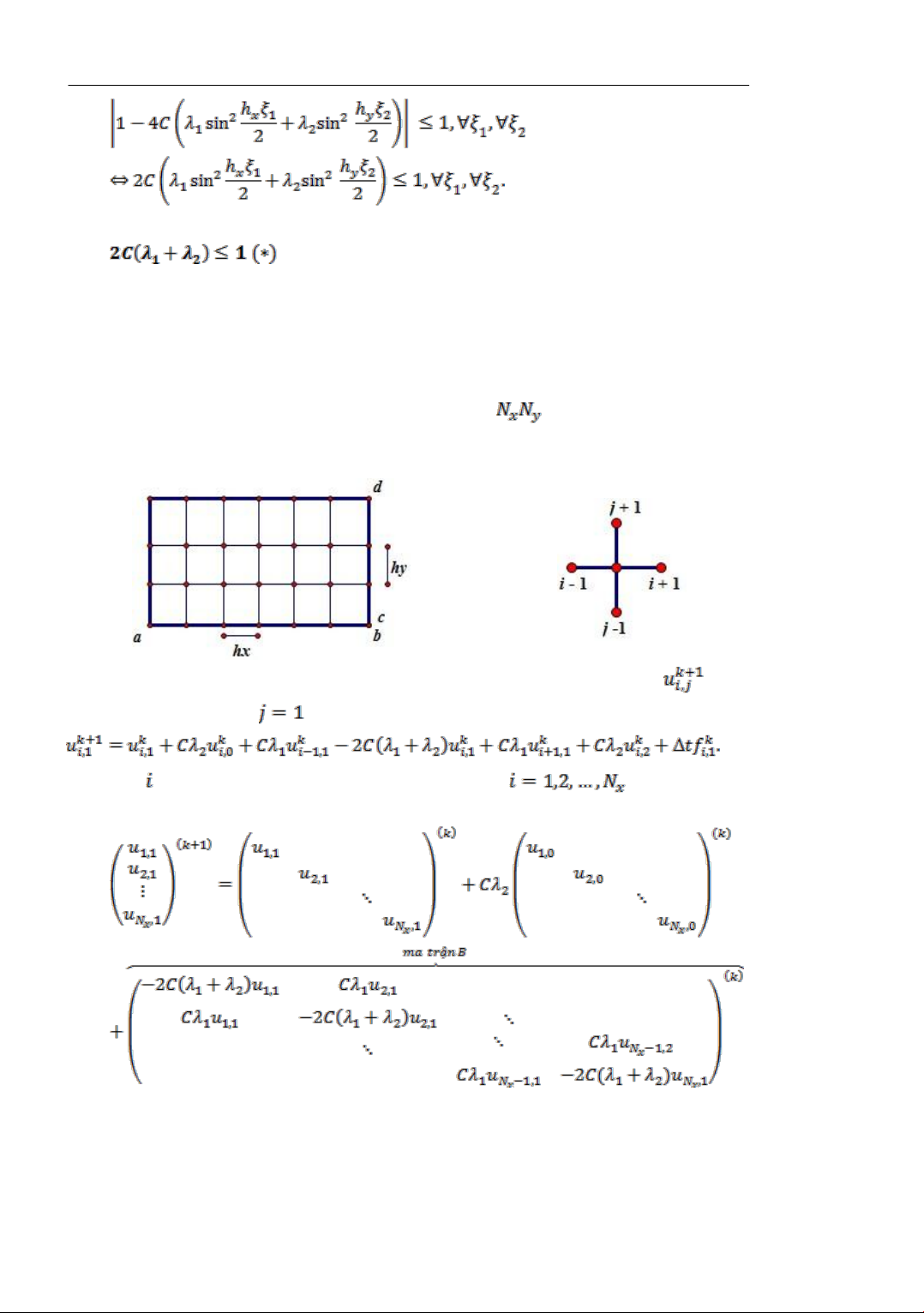
Ta phân hoạch miền Ω bởi lƣới hình chữ nhật (xem Hình 1) có các đỉnh xác định bởi
điểm với i = 1,2,...,Nx và j = 1,2,...,Ny trong đó:
Đồng thời, ta xét phân hoạch thời gian t bởi các điểm , và kí
hiệu:
Để giải gần đúng phƣơng trình (1), trƣớc tiên ta xấp xỉ các đạo hàm [1] bậc nhất theo
biến thời gian và đạo hàm bậc hai theo biến không gian bởi:
Áp dụng vào phƣơng trình (1), ta đƣợc:
Biểu diễn theo các phần tử còn lại, ta có lƣợc đồ:
trong đó:
KỈ YẾU HỘI NGHỊ SINH VIÊN NGHIÊN CỨU KHOA HỌC NĂM HỌC 2013-2014
9
1.3. Điều kiện ổn định của lược đồ
Trong phần này, chúng ta nghiên cứu điều kiện ổn định của lƣợc đồ (2) trong trƣờng
hợp không có nguồn nhiệt tác động vào hệ và điều kiện biên đồng nhất bằng không.
Nghiệm gần đúng của (1) là bộ các giá trị rời rạc có dạng . Ta
thực hiện phép biến đổi Fourier hai chiều cho nghiệm xấp xỉ trên nhƣ sau:
Ta có tính chất sau đây: Giả sử với , ta có:
Nhƣ vậy:
Nếu với , thì ,
Tƣơng tự, ta có:
- Nếu với , thì ,
- Nếu với , thì ,
- Nếu với , thì .
Áp dụng tính chất trên đây của phép biến đổi Fourier vào lƣợc đồ (2) với , ta
đƣợc:
Vì nên ta suy ra:
với
Lƣợc đồ (2) đƣợc gọi là ổn định khi và chỉ khi
tức là:
hay:
KỈ YẾU HỘI NGHỊ SINH VIÊN NGHIÊN CỨU KHOA HỌC NĂM HỌC 2013-2014
10
Từ đó suy ra :
Nhƣ vậy, ràng buộc (*) chính là điều kiện ổn định của lƣợc đồ. Trong quá trình mô
phỏng, các dữ liệu đầu vào cần phải thỏa mãn điều kiện (*) để đảm bảo thuật toán trong
máy tính hội tụ và cho kết quả tin cậy.
1.4. Dạng ma trận của lược đồ
Điều đầu tiên, ta nhận thấy với cách biểu diễn lƣợc đồ ở trên, ta đã phân hoạch miền
Ω thành lƣới chữ nhật tƣơng ứng với ma trận vuông cấp , và mỗi điểm lƣới ui,j trong
lƣợc đồ đều phải đƣợc tính từ 4 số hạng lân cận là ui−1,j (bên trái), ui+1,j (bên phải), ui,j−1
(bên trên), ui,j+1 (bên dưới):
Hình 1. Phân hoạch, sơ đồ các điểm trên lưới ảnh hướng đến việc tính
Xét lƣợc đồ (2) với , ta có:
Cho chạy, tức là viết phƣơng trình trên lần lƣợt với và biểu diễn kết
quả thu đƣợc dƣới dạng ma trận, ta có:
KỈ YẾU HỘI NGHỊ SINH VIÊN NGHIÊN CỨU KHOA HỌC NĂM HỌC 2013-2014
11
(3)
Mặt khác, quan sát ma trận , ta nhận thấy có 2 thành phần ,
không đƣợc lặp lại trong quá trình tính toán, đó cũng chính là giá trị hàm nhiệt độ xác định
ở thời điểm tm, tức là α(tm), β(tm), ở điểm biên đầu x0 và điểm biên cuối trên đƣờng
thẳng phân hoạch tại . Vì vậy, khi chuyển hệ trên thành dạng ma trận ta cần đƣa hai
thành phần này ra ngoài thành số hạng tự do (vectơ b).
Tiếp theo, ta đặt:
Khi đó, (3) đƣợc viết gọn nhƣ sau:
trong đó, I là ma trận vuông đơn vị cấp , B là ma trận vuông cấp xác định bởi:
Thực hiện tƣơng tự nhƣ trên với , ta thu đƣợc một hệ gồm
phƣơng trình tuyến tính với các biến là các vectơ chiều:
Tƣơng tự nhƣ đã xử lí với ma trận B, ta chuyển 2 phần tử mang giá trị ở biên trên và
dƣới ra một vectơ tự do. Nhƣ vậy dạng ma trận của lƣợc đồ (3) là: