93
Chƣơng 3
HÀM SỐ NHIỀU BIẾN SỐ
1. CÁC KHÁI NIỆM CƠ BẢN
1.1. Hàm số hai biến số
1.1.1. Khái niệm hàm số hai biến số
Khái niệm hàm số một biến số phản ánh sự phụ thuộc hàm số của một biến số
này vào một biến số khác: mỗi giá trị của biến độc lập đƣợc đặt tƣơng ứng với một giá
trị xác định của biến phụ thuộc. Trong thực tế, nhiều khi một biến số phụ thuộc không
chỉ vào một, mà còn phụ thuộc đồng thời vào nhiều biến số khác. Chẳng hạn, sản
lƣợng, tức là số lƣợng sản phẩm của một hãng sản xuất phụ thuộc vào mức sử dụng
các yếu tố đầu vào (gọi là các yếu tố sản xuất) nhƣ lao động, vốn v.v
Khái niệm hàm số nhiều biến số phản ánh sự phụ thuộc hàm số của một biến
số vào n biến số khác. Để cho đơn giản, trƣớc hết ta đề cập đến trƣờng hợp n = 2.
Định nghĩa.
Ta gọi biến w là hàm số của 2 biến số x và y nếu, theo một quy luật f, mỗi cặp số thực
(x,y) có thứ tự, gồm một giá trị của biến x cùng với một giá trị của biến y, đƣợc đặt
tƣơng ứng với một giá trị xác định của biến w:
f : (x, y)
w
Để biểu diễn sự phụ thuộc hàm số của biến w vào các biến x và y ta dùng ký
hiệu w = f(x, y), trong đó chữ f đặc trƣng cho quy luật tƣơng ứng nêu trong định
nghĩa. Các biến số x, y đƣợc gọi là các biến độc lập, hay các đối số của hàm số.
Khi nói đến các hàm số khác nhau ta dùng các kí hiệu khác nhau:
w = g(x, y), w = h(x, y), …
Việc thiết lập hệ tọa độ trên mặt phẳng cho phép ta đồng nhất cặp số thực có
thứ tự
00
(x , y )
với điểm M0(x0, y0) của mặt phẳng. Theo quan điểm này, một cặp biến
số (x, y) đƣợc xem nhƣ một biến điểm M(x, y) của mặt phẳng và hàm hai biến w =
f(x, y) đƣợc xem nhƣ hàm số của một biến điểm M.
Ta sẽ đồng nhất 2 cách ký hiệu: w = f(x, y) và w = f(M).
94
1.1.2. Miền xác định và miền giá trị
1. Miền xác định (MXĐ) của hàm 2 biến w = f(x, y) là tập hợp tất cả các cặp số thực
(x,y) mà các biến độc lập x và y có thể nhận đồng thời.
Nếu biểu diễn hình học thì đó là một tập hợp điểm của mặt phẳng tọa độ.
Khi cho một hàm số cụ thể ngƣời ta thƣờng cho trƣớc MXĐ và chỉ rõ luật
tƣơng ứng để khi biết một giá trị của x cùng với một giá trị của y ta có thể xác định
đƣợc giá trị tƣơng ứng của biến w. Tuy nhiên, khi xét thuần túy dƣới giác độ toán học,
ngƣời ta thƣờng cho hàm số của 2 biến x, y dƣới dạng một biểu thức f(x, y) và không
chỉ rõ MXĐ. Trong trƣờng hợp này ta coi MXĐ của hàm số là MXĐ tự nhiên của biểu
thức f(x, y), tức là tập hợp tất cả các cặp số thực (x, y) làm cho biểu thức đó có nghĩa.
Ví dụ 3.1.
MXĐ tự nhiên của hàm số w =
yx
là tập hợp tất cả các điểm M(x, y) thỏa
mãn điều kiện y
x. Về mặt hình học, đó là nửa mặt phẳng phía trên đƣờng thẳng
y = x, kể cả đƣờng thẳng này.
Ví dụ 3.2.
MXĐ tự nhiên của hàm số w = ln(4 − x2 − y2) là tập hợp tất cả các điểm
M(x, y) với x2 + y2 < 4. Đó là hình tròn có tâm ở gốc tọa độ và bán kính r = 2 (không
kể các điểm của đƣờng tròn).
Chú thích.
Tƣơng tự nhƣ trong trƣờng hợp hàm một biến, ta dùng kí hiệu f(xo, yo) để chỉ
giá trị tƣơng ứng của hàm hai biến w = f(x, y) khi gán x = xo, y = yo. Ta gọi f(xo, yo) là
giá trị của hàm số tại điểm Mo(xo, yo) và có thể dùng kí hiệu f(Mo) để thay thế.
2. Miền giá trị (MGT) của hàm số w = f(x, y) là tập hợp tất cả các giá trị của hàm số
khi điểm M(x, y) thay đổi trong MXĐ.
3. Đồ thị của hàm 2 biến.
Để biểu diễn hình học quan hệ hàm số w = f(x, y) trong không gian 3 chiều, ta
dùng hệ tọa độ vuông góc gồm 3 trục số Ox, Oy, Oz đôi một vuông góc và có cùng
gốc tọa độ O.
Miền xác định D của hàm số w = f(x, y) là một tập hợp điểm trên mặt phẳng
(Oxy). Theo quy tắc tƣơng ứng của hàm số, mỗi điểm
M(x, y)
D cho tƣơng ứng một
điểm P(
x, y, z)
trong không gian với cao độ
z
= f(
. Tập hợp tất cả các điểm
95
P(
x, y, z)
, khi điểm
M(x, y)
thay đổi trong miền D, đƣợc gọi là đồ thị của hàm số
w = f(x, y). Đồ thị thƣờng là một mặt cong trong không gian 3 chiều Oxyz.
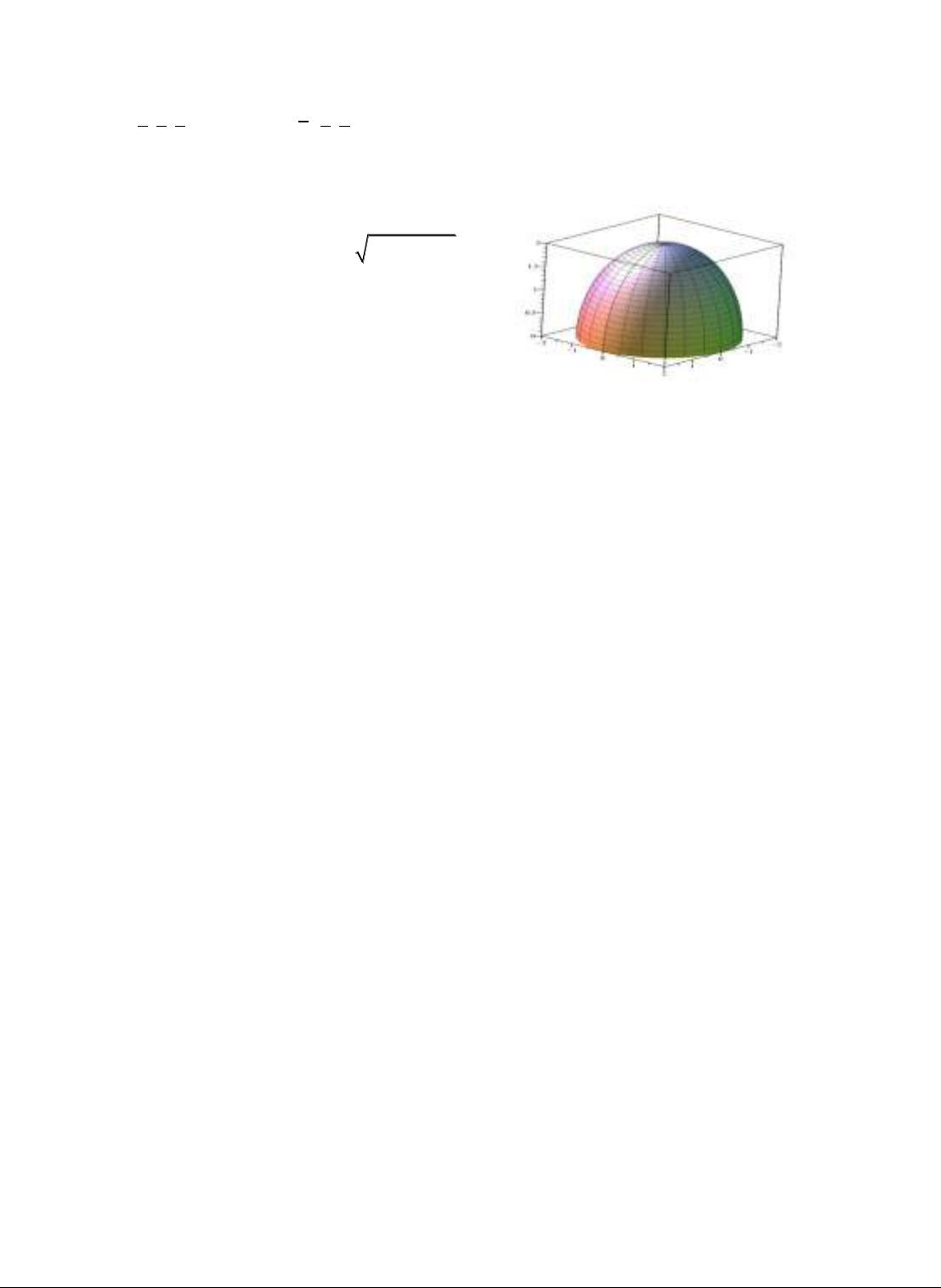
Ví dụ 3.3.
Đồ thị hàm số w =
22
4 x y
là
nửa trên của mặt cầu có tâm ở gốc tọa độ và
bán kính R = 2.
4. Đường mức.
Cho w = f(x, y) là một hàm số xác định trong miền D. Với wo là một giá trị cố
định thuộc tập giá trị của hàm w, ta xét tập hợp tất cả các điểm (x,y)
D thỏa mãn
điều kiện f(x, y) = wo
Thông thƣờng tập hợp điểm này là một đƣờng trên mặt phẳng (Oxy), đƣợc gọi
là đường mức của hàm số w = f(x,y). Nhƣ vậy, đƣờng mức của hàm số w f(x,y) là
đƣờng trên mặt phẳng (Oxy) mà dọc theo đó hàm số nhận giá trị không đổi.
Ví dụ 3.4.
Các đƣờng mức của hàm số w = 2x + 3y là các đƣờng thẳng song song
2x + 3y = C (C là hằng số).
1.2. Hàm số n biến số
1. Khái niệm hàm số hai biến số nói trên có thể khái quát hóa thành định nghĩa
tổng quát sau:
Định nghĩa.
Biến w đƣợc gọi là hàm số của n biến độc lập x1, x2,..., xn nếu, theo một quy luật f
nhất định, mỗi bộ n số thực có thứ tự (x1, x2,..., xn), trong đó mỗi số là một giá trị gán
cho biến số có cùng ký hiệu, đƣợc đặt tƣơng ứng với một giá trị xác định của biến w:
f: (x1, x2,..., xn)
w
Để diễn đạt sự phụ thuộc hàm số của biến số w vào các biến x1, x2,..., xn ta
dùng ký hiệu
w = f(x1, x2,..., xn) (1)
2. Các khái niệm MXĐ, MGT, đồ thị và đƣờng mức đƣợc hiểu theo nghĩa
tƣơng tự nhƣ đã định nghĩa cho hàm số 2 biến số.
96
3. Khái quát hóa cách biểu diễn theo tọa độ điểm trên mặt phẳng và trong
không gian 3 chiều, ta gọi mỗi bộ số thực có thứ tự (x1, x2,..., xn) là một điểm n chiều
và viết M(x1, x2,..., xn)
Theo quan niệm này mỗi bộ n biến số sắp thứ tự (x1, x2,,..., xn) có thể xem nhƣ
một biến điểm n chiều M. Khi gán cho mỗi biến số x1, x2,..., xn, một giá trị bằng số ta
đƣợc một điểm n chiều M. Hàm số n biến số w = f(x1, x2,...,xn) có thể xem nhƣ hàm số
của biến điểm M(x1, x2,..., xn) và ta có thể dùng ký hiệu w = f(M).
2. GIỚI HẠN VÀ LIÊN TỤC
2.1. Giới hạn của hàm số hai biến số
2.1.1. Giới hạn của dãy điểm trên mặt phẳng.
Nhƣ ta đã biết, khoảng cách giữa hai điểm M(x, y) và M'(x', y') trên mặt phẳng
tọa độ đƣợc xác định theo công thức
d(M, M') =
22
(x' x) (y' y)
(2)
Giả sử, theo một quy tắc nhất định, mỗi số tự nhiên k đƣợc đặt tƣơng ứng với
một điểm Mk(xk, yk) nhất định trên mặt phẳng. Khi đó ta có dãy điểm:
{ M1(x1, y2), M2(x2, y2),... , Mk(xk, yk),... }
Định nghĩa.
Nếu tồn tại một điểm cố định A(a, b) sao cho
k
lim

d(Mk, A) = 0 thì ta nói rằng dãy
k
M
hội tụ đến điểm A, hay điểm A là giới hạn của dãy điểm
k
M
khi k

và ký
hiệu nhƣ sau:
kk
k
limM A hay M A khi k

Dựa vào công thức xác định khoảng cách (2) ta dễ dàng chứng minh:
Định lý.
Dãy điểm Mk(xk, yk) hội tụ đến điểm A(a, b) khi và chỉ khi
k
k
lim x a

và
k
k
lim y b

97
Ví dụ 3.6.
Để tìm giới hạn của dãy điểm
k
1k
M,
k k 1






ta tính giới hạn của các dãy số
kk
1k
x , y
k k 1

:
kk
k k k k
1k
lim x lim 0, lim y lim 1
k k 1
   
Vậy Mk
1k
, A 0,1 khi k
k k 1



2.1.2. Giới hạn của hàm số
Cho hàm số w = f(x, y) = f(M) xác định trong miền D. Giả sử A(a, b) là một
điểm cố định của mặt phẳng sao cho tồn tại các dãy điểm
k k k
M x ,y
của miền D
hội tụ đến điểm A (điểm A có thể thuộc miền D hoặc không).
Lý thuyết giới hạn xem xét diễn biến của biến phụ thuộc w khi điểm M(x, y)
thay đổi trong miền D và tiến dần đến điểm A, tức là thu hẹp một cách tùy ý khoảng
cách từ điểm M đến điểm A (với giả thiết M
A). Quá trình này đƣợc ký hiệu là:
M A hay x a, y b
Theo quy luật hàm số, mỗi dãy điểm
{
1 1 1 2 2 2 k k k
M x ,y , M x ,y ,..., M x ,y ,...
} (3)
cho tƣơng ứng một dãy số
{ w1 = f(M1), w2 = (M2), ... , wk = f(Mk),... } (4)
Dãy số (4) là dãy các giá trị của hàm số w = f(x,y) = f(M) tƣơng ứng với dãy
điểm (3) lấy từ miền xác định D.
Định nghĩa
Nếu với mọi dãy điểm (3) lấy từ miền xác định D của hàm số w = f(x, y) và hội tụ đến
điểm A(a, b), dãy số (4) tƣơng ứng luôn luôn có giới hạn L thì số L đƣợc gọi là giới
hạn của hàm số đã cho khi M
A (hay x
a, y
b) và ký hiệu nhƣ sau:
MA
lim f (M) L,
hoặc
xa
yb
limf (x, y) L