CH NG IIIƯƠ
Đ THỒ Ị
Lý thuy t đ th là m t ngành khoa h c đ c phát tri n t lâu nh ng l i cóế ồ ị ộ ọ ượ ể ừ ư ạ
nhi u ng d ng hi n đ i. Nh ng ý t ng c b n c a nó đ c đ a ra t th k 18 b iề ứ ụ ệ ạ ữ ưở ơ ả ủ ượ ư ừ ế ỷ ở
nhà toán h c Th y Sĩ tên là Leonhard Euler. Ông đã dùng đ th đ gi i quy t bài toánọ ụ ồ ị ể ả ế
7 chi c c u Konigsberg n i ti ng.ế ầ ổ ế
Đ th cũng đ c dùng đ gi i các bài toán trong nhi u lĩnh v c khác nhau. Thíồ ị ượ ể ả ề ự
d , dùng đ th đ xác đ nh xem có th c hi n m t m ch đi n trên m t b ng đi nụ ồ ị ể ị ự ệ ộ ạ ệ ộ ả ệ
ph ng đ c không. Chúng ta cũng có th phân bi t hai h p ch t hóa h c có cùng côngẳ ượ ể ệ ợ ấ ọ
th c phân t nh ng có c u trúc khác nhau nh đ th . Chúng ta cũng có th xác đ nhứ ử ư ấ ờ ồ ị ể ị
xem hai máy tính có đ c n i v i nhau b ng m t đ ng truy n thông hay không n uượ ố ớ ằ ộ ườ ề ế
dùng mô hình đ th m ng máy tính. Đ th v i các tr ng s đ c gán cho các c nhồ ị ạ ồ ị ớ ọ ố ượ ạ
c a nó có th dùng đ gi i các bài toán nh bài toán tìm đ ng đi ng n nh t gi a haiủ ể ể ả ư ườ ắ ấ ữ
thành ph trong m t m ng giao thông. Chúng ta cũng có th dùng đ th đ l p l ch thiố ộ ạ ể ồ ị ể ậ ị
và phân chia kênh cho các đài truy n hình.ề
3.1. Đ NH NGHĨA VÀ THÍ D .Ị Ụ
Đ th là m t c u trúc r i r c g m các đ nh và các c nh (vô h ng ho c cóồ ị ộ ấ ờ ạ ồ ỉ ạ ướ ặ
h ng) n i các đ nh đó. Ng i ta phân lo i đ th tùy theo đ c tính và s các c nh n iướ ố ỉ ườ ạ ồ ị ặ ố ạ ố
các c p đ nh c a đ th . Nhi u bài toán thu c nh ng lĩnh v c r t khác nhau có th gi iặ ỉ ủ ồ ị ề ộ ữ ự ấ ể ả
đ c b ng mô hình đ th . Ch ng h n ng i ta có th dùng đ th đ bi u di n sượ ằ ồ ị ẳ ạ ườ ể ồ ị ể ể ễ ự
c nh tranh các loài trong m t môi tr ng sinh thái, dùng đ th đ bi u di n ai có nhạ ộ ườ ồ ị ể ể ễ ả
h ng lên ai trong m t t ch c nào đó, và cũng có th dùng đ th đ bi u di n cácưở ộ ổ ứ ể ồ ị ể ể ễ
k t c c c a cu c thi đ u th thao. Chúng ta cũng có th dùng đ th đ gi i các bàiế ụ ủ ộ ấ ể ể ồ ị ể ả
toán nh bài toán tính s các t h p khác nhau c a các chuy n bay gi a hai thành phư ố ổ ợ ủ ế ữ ố
trong m t m ng hàng không, hay đ gi i bài toán đi tham quan t t c các đ ng phộ ạ ể ả ấ ả ườ ố
c a m t thành ph sao cho m i đ ng ph đi qua đúng m t l n, ho c bài toán tìm sủ ộ ố ỗ ườ ố ộ ầ ặ ố
các màu c n thi t đ tô các vùng khác nhau c a m t b n đ .ầ ế ể ủ ộ ả ồ
Trong đ i s ng, chúng ta th ng g p nh ng s đ , nh s đ t ch c b máy,ờ ố ườ ặ ữ ơ ồ ư ơ ồ ổ ứ ộ
s đ giao thông, s đ h ng d n th t đ c các ch ng trong m t cu n sách, ...,ơ ồ ơ ồ ướ ẫ ứ ự ọ ươ ộ ố
g m nh ng đi m bi u th các đ i t ng đ c xem xét (ng i, t ch c, đ a danh,ồ ữ ể ể ị ố ượ ượ ườ ổ ứ ị
ch ng m c sách, ...) và n i m t s đi m v i nhau b ng nh ng đo n th ng (ho cươ ụ ố ộ ố ể ớ ằ ữ ạ ẳ ặ
cong) hay nh ng mũi tên, t ng tr ng cho m t quan h nào đó gi a các đ i t ng. Đóữ ượ ư ộ ệ ữ ố ượ
là nh ng thí d v đ th .ữ ụ ề ồ ị
3.1.1. Đ nh nghĩa:ị M t đ n đ th G = (V, E) g m m t t p khác r ng V mà các ph nộ ơ ồ ị ồ ộ ậ ỗ ầ
t c a nó g i là các đ nh và m t t p E mà các ph n t c a nó g i là các c nh, đó là cácử ủ ọ ỉ ộ ậ ầ ử ủ ọ ạ
c p không có th t c a các đ nh phân bi t.ặ ứ ự ủ ỉ ệ
37
3.1.2. Đ nh nghĩa:ị M t đa đ th G = (V, E) g m m t t p khác r ng V mà các ph nộ ồ ị ồ ộ ậ ỗ ầ
t c a nó g i là các đ nh và m t h E mà các ph n t c a nó g i là các c nh, đó là cácử ủ ọ ỉ ộ ọ ầ ử ủ ọ ạ
c p không có th t c a các đ nh phân bi t. Hai c nh đ c g i là c nh b i hay songặ ứ ự ủ ỉ ệ ạ ượ ọ ạ ộ
song n u chúng cùng t ng ng v i m t c p đ nh.ế ươ ứ ớ ộ ặ ỉ
Rõ ràng m i đ n đ th là đa đ th , nh ng không ph i đa đ th nào cũng là đ nỗ ơ ồ ị ồ ị ư ả ồ ị ơ
đ th .ồ ị
3.1.3. Đ nh nghĩa:ị M t gi đ th G = (V, E) g m m t t p khác r ng V mà các ph nộ ả ồ ị ồ ộ ậ ỗ ầ
t c a nó g i là các đ nh và m t h E mà các ph n t c a nó g i là các c nh, đó là cácử ủ ọ ỉ ộ ọ ầ ử ủ ọ ạ
c p không có th t c a các đ nh (không nh t thi t là phân bi t).ặ ứ ự ủ ỉ ấ ế ệ
V i vớ∈V, n u (v,v)ế∈E thì ta nói có m t khuyên t i đ nh v.ộ ạ ỉ
Tóm l i, gi đ th là lo i đ th vô h ng t ng quát nh t vì nó có th ch a cácạ ả ồ ị ạ ồ ị ướ ổ ấ ể ứ
khuyên và các c nh b i. Đa đ th là lo i đ th vô h ng có th ch a c nh b i nh ngạ ộ ồ ị ạ ồ ị ướ ể ứ ạ ộ ư
không th có các khuyên, còn đ n đ th là lo i đ th vô h ng không ch a c nh b iể ơ ồ ị ạ ồ ị ướ ứ ạ ộ
ho c các khuyên.ặ
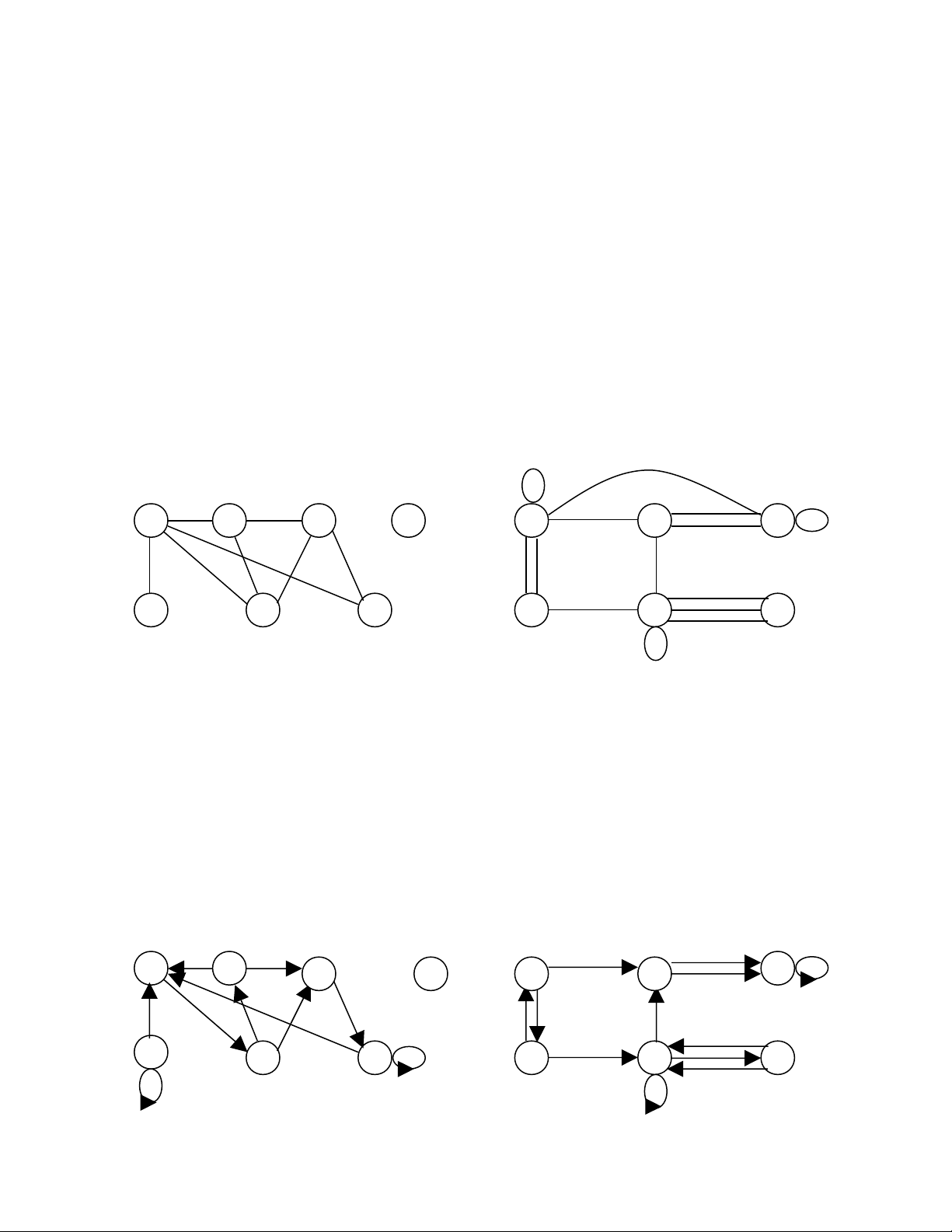
Thí d 1:ụ
Đ n đ th ơ ồ ị
Gi đ thả ồ ị
3.1.4. Đ nh nghĩa:ị M t đ th có h ng G = (V, E) g m m t t p khác r ng V mà cácộ ồ ị ướ ồ ộ ậ ỗ
ph n t c a nó g i là các đ nh và m t t p E mà các ph n t c a nó g i là các cung, đóầ ử ủ ọ ỉ ộ ậ ầ ử ủ ọ
là các c p có th t c a các ph n t thu c V.ặ ứ ự ủ ầ ử ộ
3.1.5. Đ nh nghĩa:ị M t đa đ th có h ng G = (V, E) g m m t t p khác r ng V màộ ồ ị ướ ồ ộ ậ ỗ
các ph n t c a nó g i là các đ nh và m t h E mà các ph n t c a nó g i là các cung,ầ ử ủ ọ ỉ ộ ọ ầ ử ủ ọ
đó là các c p có th t c a các ph n t thu c V.ặ ứ ự ủ ầ ử ộ
Đ th vô h ng nh n đ c t đ th có h ng G b ng cách xoá b các chi uồ ị ướ ậ ượ ừ ồ ị ướ ằ ỏ ề
mũi tên trên các cung đ c g i là đ th vô h ng n n c a G.ượ ọ ồ ị ướ ề ủ
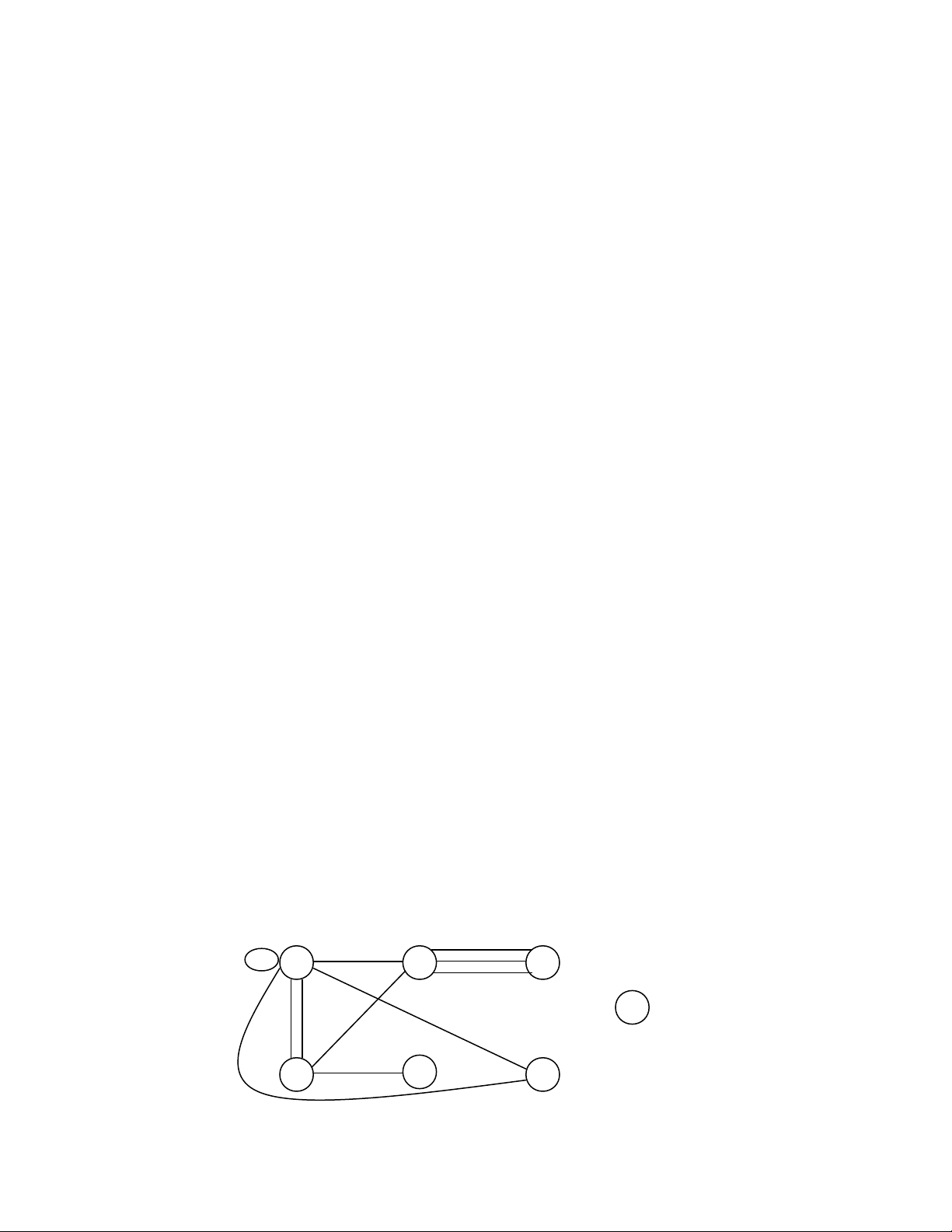
Thí d 2:ụ
Đ th có h ng Đa đ th có h ng ồ ị ướ ồ ị ướ
38
v1
v2
v3
v4
v5
v6
v7
v1
v2
v3
v4
v5
v6
v6
v7
v3
v4
v5
v6
v1
v2
v3
v5
V5
v1
v2
Thí d 3: 1) Đ thụ ồ ị “l n t ” trong sinh thái h cấ ổ ọ . Đ th đ c dùng trong nhi u môồ ị ượ ề
hình có tính đ n s t ng tác c a các loài v t. Ch ng h n s c nh tranh c a các loàiế ự ươ ủ ậ ẳ ạ ự ạ ủ
trong m t h sinh thái có th mô hình hóa b ng đ th “l n t ”. M i loài đ c bi uộ ệ ể ằ ồ ị ấ ổ ỗ ượ ể
di n b ng m t đ nh. M t c nh vô h ng n i hai đ nh n u hai loài đ c bi u di nễ ằ ộ ỉ ộ ạ ướ ố ỉ ế ượ ể ễ
b ng các đ nh này là c nh tranh v i nhau.ằ ỉ ạ ớ
2) Đ th nh h ngồ ị ả ưở . Khi nghiên c u tính cách c a m t nhóm ngu i, ta th y m t sứ ủ ộ ờ ấ ộ ố
ng i có th có nh h ng lên suy nghĩ c a nh ng ng i khác. Đ th có h ng đ cườ ể ả ưở ủ ữ ườ ồ ị ướ ượ
g i là đ th nh h ngọ ồ ị ả ưở có th dùng đ mô hình bài toán này. M i ng i c a nhómể ể ỗ ườ ủ
đ c bi u di n b ng m t đ nh. Khi m t ng i đ c bi u di n b ng đ nh a có nhượ ể ễ ằ ộ ỉ ộ ườ ượ ể ễ ằ ỉ ả
h ng lên ng i đ c bi u di n b ng đ nh b thì có m t cung n i t đ nh a đ n đ nh b.ưở ườ ượ ể ễ ằ ỉ ộ ố ừ ỉ ế ỉ
3) Thi đ u vòng tròn.ấ M t cu c thi đ u th thao trong đó m i đ i đ u v i m i đ iộ ộ ấ ể ỗ ộ ấ ớ ỗ ộ
khác đúng m t l n g i là đ u vòng tròn. Cu c thi đ u nh th có th đ c mô hìnhộ ầ ọ ấ ộ ấ ư ế ể ượ
b ng m t đ th có h ng trong đó m i đ i là m t đ nh. M t cung đi t đ nh a đ nằ ộ ồ ị ướ ỗ ộ ộ ỉ ộ ừ ỉ ế
đ nh b n u đ i a th ng đ i b.ỉ ế ộ ắ ộ
4) Các ch ng trình máy tính có th thi hành nhanh h n b ng cách thi hành đ ng th iươ ể ơ ằ ồ ờ
m t s câu l nh nào đó. Đi u quan tr ng là không đ c th c hi n m t câu l nh đòiộ ố ệ ề ọ ượ ự ệ ộ ệ
h i k t qu c a câu l nh khác ch a đ c th c hi n. S ph thu c c a các câu l nhỏ ế ả ủ ệ ư ượ ự ệ ự ụ ộ ủ ệ
vào các câu l nh tr c có th bi u di n b ng m t đ th có h ng. M i câu l nhệ ướ ể ể ễ ằ ộ ồ ị ướ ỗ ệ
đ c bi u di n b ng m t đ nh và có m t cung t m t đ nh t i m t đ nh khác n u câuượ ể ễ ằ ộ ỉ ộ ừ ộ ỉ ớ ộ ỉ ế
l nh đ c bi u di n b ng đ nh th hai không th th c hi n đ c tr c khi câu l nhệ ượ ể ễ ằ ỉ ứ ể ự ệ ượ ướ ệ
đ c bi u di n b ng đ nh th nh t đ c th c hi n. Đ th này đ c g i làượ ể ễ ằ ỉ ứ ấ ượ ự ệ ồ ị ượ ọ đ th cóồ ị
u tiên tr c sauư ướ .
3.2. B C C A Đ NH.Ậ Ủ Ỉ
3.2.1. Đ nh nghĩa: ịHai đ nh u và v trong đ th (vô h ng) G=(V,E) đ c g i là li nỉ ồ ị ướ ượ ọ ề
k n u (u,v)ề ế ∈E. N u e = (u,v) thì e g i là c nh liên thu c v i các đ nh u và v. C nh eế ọ ạ ộ ớ ỉ ạ
cũng đ c g i là c nh n i các đ nh u và v. Các đ nh u và v g i là các đi m đ u mútượ ọ ạ ố ỉ ỉ ọ ể ầ
c a c nh e.ủ ạ
3.2.2. Đ nh nghĩa:ị B c c a đ nh v trong đ th G=(V,E), ký hi u deg(v), là s cácậ ủ ỉ ồ ị ệ ố
c nh liên thu c v i nó, riêng khuyên t i m t đ nh đ c tính hai l n cho b c c a nó.ạ ộ ớ ạ ộ ỉ ượ ầ ậ ủ
Đ nh v g i là đ nh treo n u deg(v)=1 và g i là đ nh cô l p n u deg(v)=0.ỉ ọ ỉ ế ọ ỉ ậ ế
Thí d 4: ụ
39
v1
v2
v3
v4
v5
v6
v7
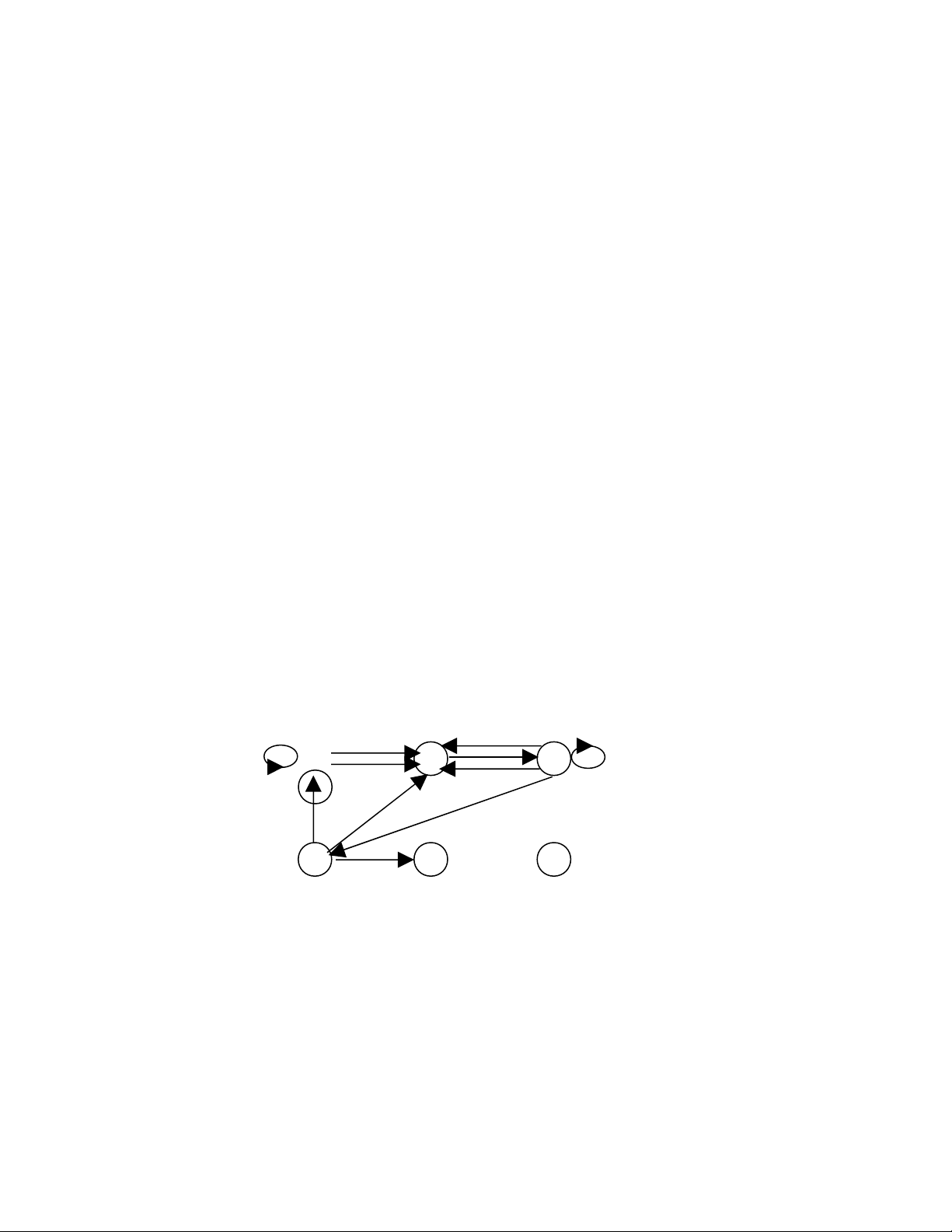
Ta có deg(v1)=7, deg(v2)=5, deg(v3)=3, deg(v4)=0, deg(v5)=4, deg(v6)=1, deg(v7)=2. Đ nhỉ
v4 là đ nh cô l p và đ nh vỉ ậ ỉ 6 là đ nh treo.ỉ
3.2.3. M nh đ :ệ ề Cho đ th G = (V, E). Khi đó ồ ị
2|E| =
∑
∈Vv
v)deg(
.
Ch ng minh:ứ Rõ ràng m i c nh e = (u,v) đ c tính m t l n trong deg(u) và m t l nỗ ạ ượ ộ ầ ộ ầ
trong deg(v). T đó suy ra t ng t t c các b c c a các đ nh b ng hai l n s c nh.ừ ổ ấ ả ậ ủ ỉ ằ ầ ố ạ
3.2.4. H qu :ệ ả S đ nh b c l c a m t đ th là m t s ch n.ố ỉ ậ ẻ ủ ộ ồ ị ộ ố ẵ
Ch ng minh:ứ G i Vọ1 và V2 t ng ng là t p các đ nh b c ch n và t p các đ nh b c lươ ứ ậ ỉ ậ ẵ ậ ỉ ậ ẻ
c a đ th G = (V, E). Khi đóủ ồ ị
2|E| =
∑
∈1
)deg(
Vv
v
+
∑
∈2
)deg(
Vv
v
V trái là m t s ch n và t ng th nh t cũng là m t s ch n nên t ng th hai là m tế ộ ố ẵ ổ ứ ấ ộ ố ẵ ổ ứ ộ
s ch n. Vì deg(v) là l v i m i v ố ẵ ẻ ớ ọ ∈ V2 nên |V2| là m t s ch n.ộ ố ẵ
3.2.5. M nh đ : ệ ề Trong m t đ n đ th , luôn t n t i hai đ nh có cùng b c.ộ ơ ồ ị ồ ạ ỉ ậ
Ch ng minh: ứXét đ n đ th G=(V,E) có |V|=n. Khi đó phát bi u trên đ c đ a v bàiơ ồ ị ể ượ ư ề
toán: trong m t phòng h p có n ng i, bao gi cũng tìm đ c 2 ng i có s ng iộ ọ ườ ờ ượ ườ ố ườ
quen trong s nh ng ng i d h p là nh nhau (xem Thí d 6 c a 2.2.3).ố ữ ườ ự ọ ư ụ ủ
3.2.6. Đ nh nghĩa:ị Đ nh u đ c g i là n i t i v hay v đ c g i là đ c n i t uỉ ượ ọ ố ớ ượ ọ ượ ố ừ
trong đ th có h ng G n u (u,v) là m t cung c a G. Đ nh u g i là đ nh đ u và đ nh vồ ị ướ ế ộ ủ ỉ ọ ỉ ầ ỉ
g i là đ nh cu i c a cung này.ọ ỉ ố ủ
3.2.7. Đ nh nghĩa:ị B c vào (t. . b c ra) c a đ nh v trong đ th có h ng G, ký hi uậ ư ậ ủ ỉ ồ ị ướ ệ
degt(v) (t. . degưo(v)), là s các cung có đ nh cu i là v.ố ỉ ố
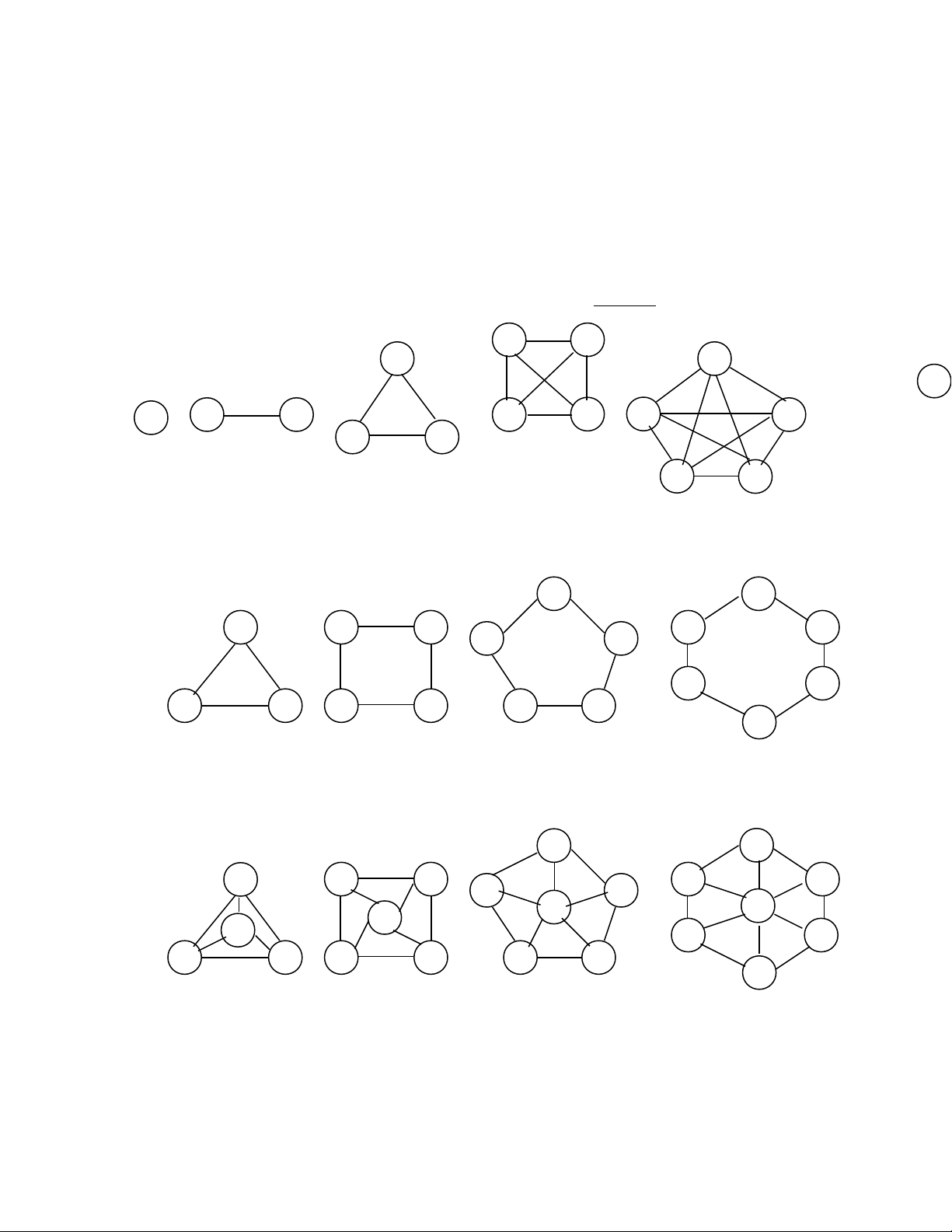
Thí d 5:ụ
degt(v1) = 2, dego(v1) = 3,
degt(v2) = 5, dego(v2) = 1,
degt(v3) = 2, dego(v3) = 4,
degt(v4) = 1, deg0(v4) = 3,
degt(v5) = 1, dego(v5) = 0,
degt(v6) = 0, dego(v6) = 0.
Đ nh có b c vào và b c ra cùng b ng 0 g i là đ nh cô l p. Đ nh có b c vào b ngỉ ậ ậ ằ ọ ỉ ậ ỉ ậ ằ
1 và b c ra b ng 0 g i là đ nh treo, cung có đ nh cu i là đ nh treo g i là cung treo.ậ ằ ọ ỉ ỉ ố ỉ ọ
40
v1
v2
v3
v4
v5
v6
3.2.8. M nh đ : ệ ề Cho G =(V, E) là m t đ th có h ng. Khi đó ộ ồ ị ướ
∑ ∑
∈ ∈
=
Vv Vv
ot vv )(deg)(deg
= |E|.
Ch ng minh:ứ K t qu có ngay là vì m i cung đ c tính m t l n cho đ nh đ u và m tế ả ỗ ượ ộ ầ ỉ ầ ộ
l n cho đ nh cu i.ầ ỉ ố
3.3. NH NG Đ N Đ TH Đ C BI T.Ữ Ơ Ồ Ị Ặ Ệ
3.3.1. Đ th đ y đ :ồ ị ầ ủ Đ th đ y đ n đ nh, ký hi u là Kồ ị ầ ủ ỉ ệ n, là đ n đ th mà hai đ nhơ ồ ị ỉ
phân bi t b t kỳ c a nó luôn li n k . Nh v y, Kệ ấ ủ ề ề ư ậ n có
2
)1( −nn
c nh và m i đ nh c aạ ỗ ỉ ủ
Kn có b c là nậ−1.
Thí d 6:ụ
K1 K2
K3 K4
K5
3.3.2. Đ th vòng:ồ ị Đ n đ th n đ nh vơ ồ ị ỉ 1, v2, ..., vn (n≥3) và n c nh (vạ1,v2), (v2,v3), ...,
(vn-1,vn), (vn,v1) đ c g i là đ th vòng, ký hi u là Cượ ọ ồ ị ệ n. Nh v y, m i đ nh c a Cư ậ ỗ ỉ ủ n có
b c là 2.ậ
Thí d 7:ụ
C3 C4 C5 C6
3.3.3. Đ th bánh xe:ồ ị T đ th vòng Cừ ồ ị n, thêm vào đ nh vỉn+1 và các c nh (vạn+1,v1),
(vn+1,v2), ..., (vn+1,vn), ta nh n đ c đ n đ th g i là đ th bánh xe, ký hi u là Wậ ượ ơ ồ ị ọ ồ ị ệ n. Như
v y, đ th Wậ ồ ị n có n+1 đ nh, 2n c nh, m t đ nh b c n và n đ nh b c 3.ỉ ạ ộ ỉ ậ ỉ ậ
Thí d 8:ụ
W3 W4 W5 W6
3.3.4. Đ th l p ph ng:ồ ị ậ ươ Đ n đ th 2ơ ồ ị n đ nh, t ng ng v i 2ỉ ươ ứ ớ n xâu nh phân đị ộ
dài n và hai đ nh k nhau khi và ch khi 2 xâu nh phân t ng ng v i hai đ nh này chỉ ề ỉ ị ươ ứ ớ ỉ ỉ
41
v1
v1
v2
v1
v2
v3
v1
v2
v3
v4
v5
v1
v2
v1
v3
V4
v1
v2
v3
v1
v2
v4
v3
v1
v5
v2
v4
v3
v1
v6
v5
v2
v3
v4
v2
v3
v1
v2
v4
v3
v1
v5
v2
v4
v3
v6
v5
v2
v3
v4
v1
v4
v5
v6
v7
v1