CH NG VIIƯƠ
Đ TH PH NG VÀ TÔ MÀU Đ THỒ Ị Ẳ Ồ Ị
T xa x a đã l u truy n m t bài toán c “Ba nhà, ba gi ng”: Có ba nhà g nừ ư ư ề ộ ổ ế ở ầ
ba cái gi ng, nh ng không có đ ng n i th ng các nhà v i nhau cũng nh không cóế ư ườ ố ẳ ớ ư
đ ng n i th ng các gi ng v i nhau.ườ ố ẳ ế ớ
Có l n b t hoà v i nhau, h tìm cách làm ầ ấ ớ ọ
các đ ng khác đ n gi ng sao cho các đ ng nàyườ ế ế ườ
đôi m t không giao nhau. H có th c hi n đ c ýộ ọ ự ệ ượ
đ nh đó không?ị
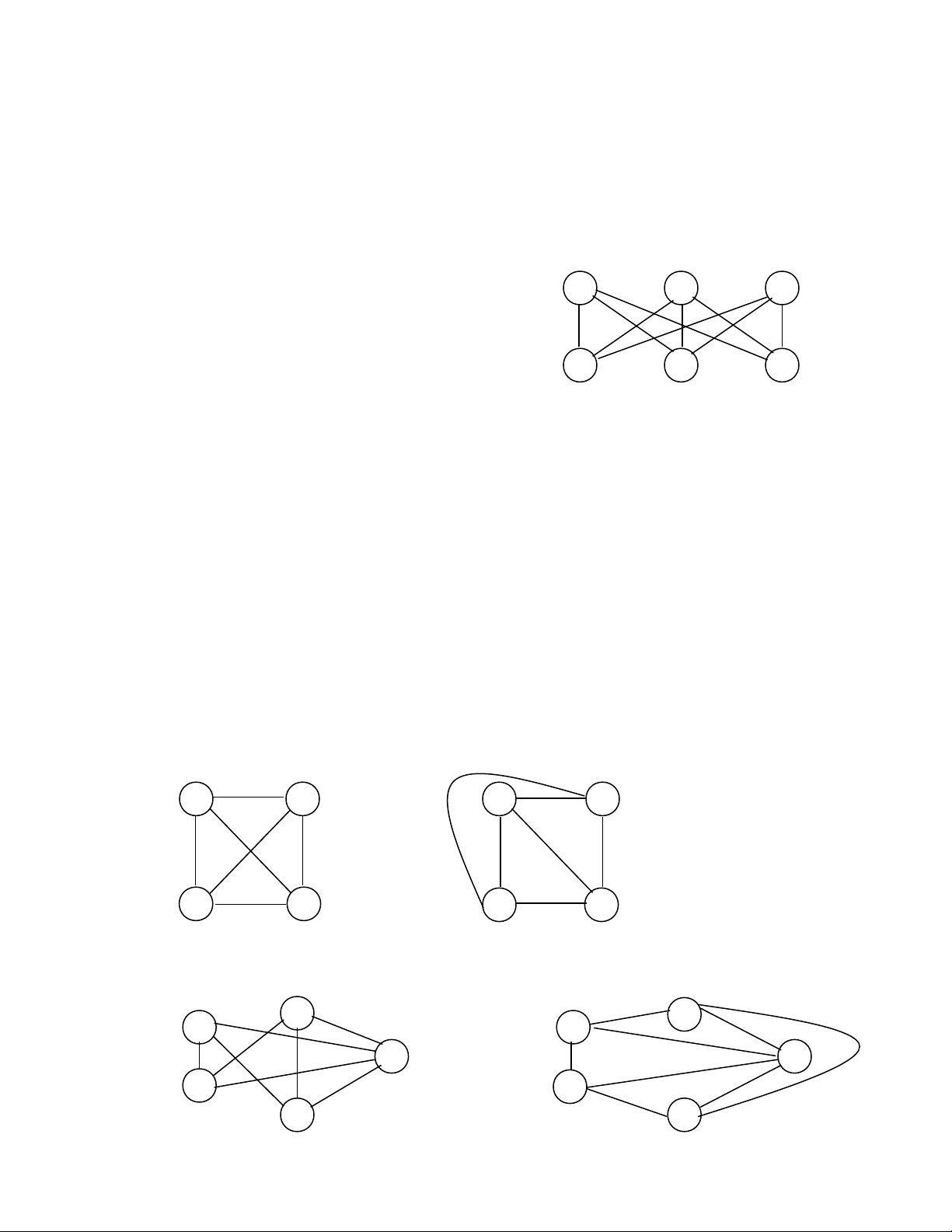
Bài toán này có th đ c mô hình b ng đ th phân đôi đ y đ Kể ượ ằ ồ ị ầ ủ 3,3. Câu h i banỏ
đ u có th di n đ t nh sau: Có th v Kầ ể ễ ạ ư ể ẽ 3,3 trên m t m t ph ng sao cho không có haiộ ặ ẳ
c nh nào c t nhau? Trong ch ng này chúng ta s nghiên c u bài toán: có th v m tạ ắ ươ ẽ ứ ể ẽ ộ
đ th trên m t m t ph ng không có các c nh nào c t nhau không. Đ c bi t chúng ta sồ ị ộ ặ ẳ ạ ắ ặ ệ ẽ
tr l i bài toán ba nhà ba gi ng. Th ng có nhi u cách bi u di n đ th . Khi nào có thả ờ ế ườ ề ể ễ ồ ị ể
tìm đ c ít nh t m t cách bi u di n đ th không có c nh c t nhau?ượ ấ ộ ể ễ ồ ị ạ ắ
7.1. Đ TH PH NG.Ồ Ị Ẳ
7.1.1. Đ nh nghĩa:ị M t đ th đ c g i là ph ng n u nó có th v đ c trên m tộ ồ ị ượ ọ ẳ ế ể ẽ ượ ộ
m t ph ng mà không có các c nh nào c t nhau ( m t đi m không ph i là đi m mútặ ẳ ạ ắ ở ộ ể ả ể
c a các c nh). Hình v nh th g i là m t bi u di n ph ng c a đ th .ủ ạ ẽ ư ế ọ ộ ể ễ ẳ ủ ồ ị
M t đ th có th là ph ng ngay c khi nó th ng đ c v v i nh ng c nh c tộ ồ ị ể ẳ ả ườ ượ ẽ ớ ữ ạ ắ
nhau, vì có th v nó b ng cách khác không có các c nh c t nhau.ể ẽ ằ ạ ắ
Thí d 1:ụ 1) M t cây, m t chu trình đ n là m t đ th ph ng.ộ ộ ơ ộ ồ ị ẳ
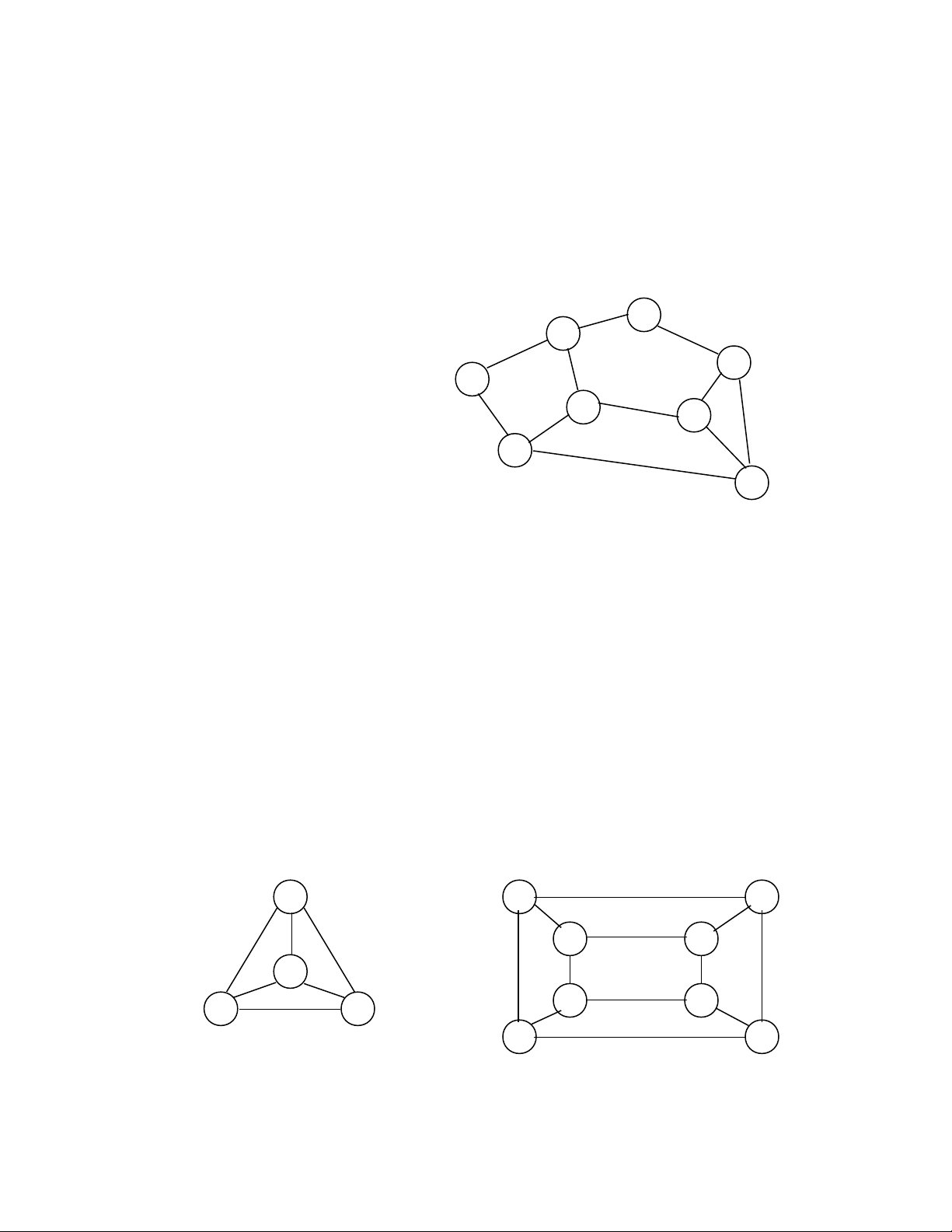
2) K4 là đ th ph ng b i vì có th v l i nh hình bên không có đ ng c t nhauồ ị ẳ ở ể ẽ ạ ư ườ ắ
Đ th Kồ ị 4 K4 v không có đ ng c t nhauẽ ườ ắ
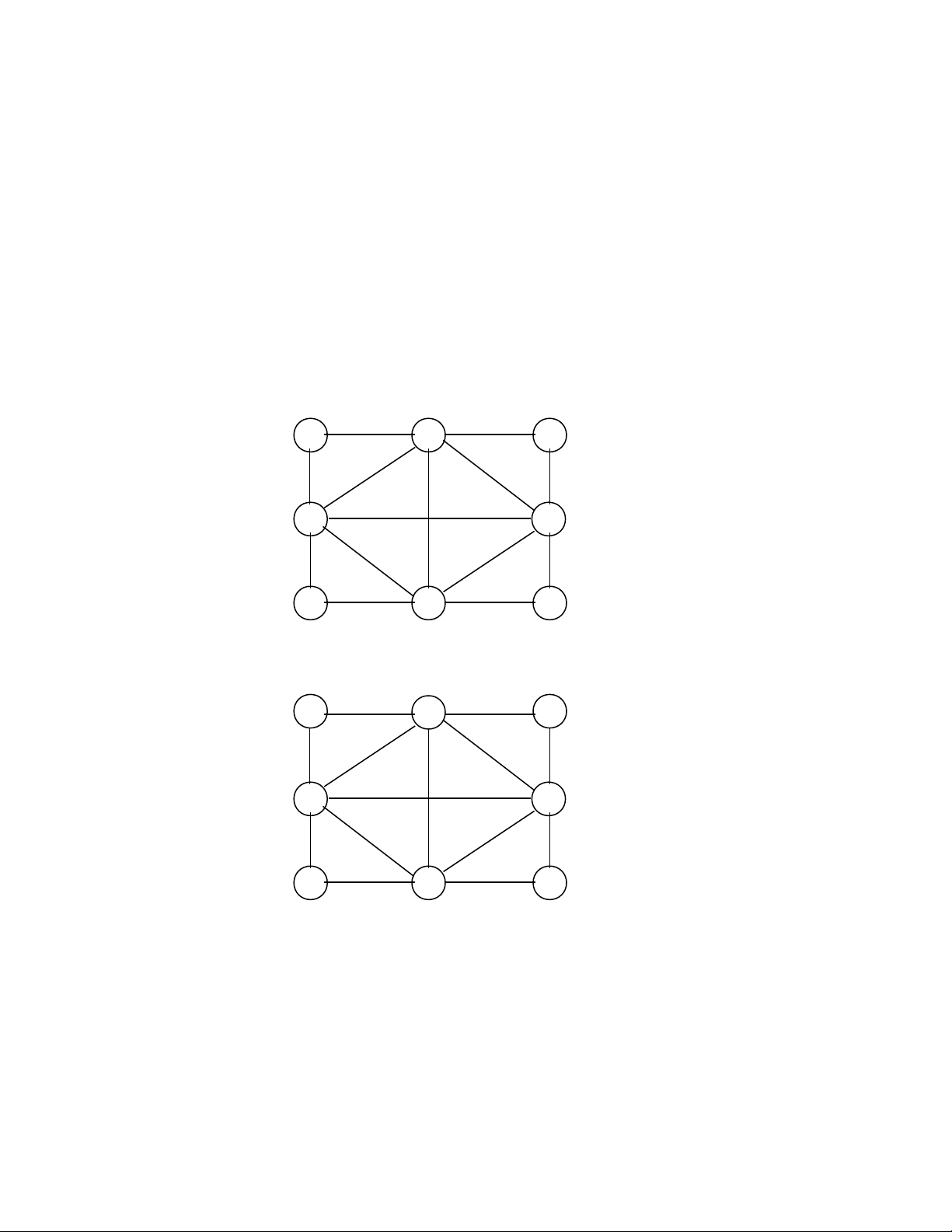
3) Xét đ th G nh trong hình a d i đây. Có th bi u di n G m t cách khác nh trongồ ị ư ướ ể ể ễ ộ ư
hình b, trong đó b t kỳ hai c nh nào cũng không c t nhau.ấ ạ ắ
104
N1
N2
N3
G2
G3
G1
a
dc
b a b
c d
db
c
a
e
e
d
b
c
a
4) Đ th đ y đ Kồ ị ầ ủ 5 là m t thí d v đ th không ph ng (xem Đ nh lý 7.2.2).ộ ụ ề ồ ị ẳ ị
7.1.2. Đ nh nghĩa:ị Cho G là m t đ th ph ng. M i ph n m t ph ng gi i h n b iộ ồ ị ẳ ỗ ầ ặ ẳ ớ ạ ở
m t chu trình đ n không ch a bên trong nó m t chu trình đ n khác, g i là m t mi nộ ơ ứ ộ ơ ọ ộ ề
(h u h n) c a đ th G. Chu trình gi i h n mi n là biên c a mi n. M i đ th ph ngữ ạ ủ ồ ị ớ ạ ề ủ ề ỗ ồ ị ẳ
liên thông có m t mi n vô h n duy nh t (là ph n m t ph ng bên ngoài t t c các mi nộ ề ạ ấ ầ ặ ẳ ấ ả ề
h u h n). S c nh ít nh t t o thành biên g i là đai c a G; tr ng h p n u G không cóữ ạ ố ạ ấ ạ ọ ủ ườ ợ ế
chu trình thì đai chính là s c nh c a G.ố ạ ủ
Thí d 2:ụ 1) M t cây ch có m t mi n, đó là mi n vô h n.ộ ỉ ộ ề ề ạ
2) Đ th ph ng hình bên có 5 mi n, Mồ ị ẳ ở ề 5
là mi n vô h n, mi n Mề ạ ề 1 có biên abgfa,
mi n Mề2 có biên là bcdhgb, … Chu
trình đ n abcdhgfa không gi i h n m tơ ớ ạ ộ
mi n vì ch a bên trong nó chu trình ề ứ đ nơ
khác là abgfa.
7.1.3. Đ nh lý (Euler, 1752):ị N u m t đ th ph ng liên thông có n đ nh, p c nh và dế ộ ồ ị ẳ ỉ ạ
mi n thì ta có h th c:ề ệ ứ
n − p + d = 2.
Ch ng minh:ứ Cho G là đ th ph ng liên thông có n đ nh, p c nh và d mi n.ồ ị ẳ ỉ ạ ề
Ta b m t s c nh c a G đ đ c m t cây khung c a G. M i l n ta b m tỏ ộ ố ạ ủ ể ượ ộ ủ ỗ ầ ỏ ộ
c nh (p gi m 1) thì s mi n c a G cũng gi m 1 (d gi m 1), còn s đ nh c a G khôngạ ả ố ề ủ ả ả ố ỉ ủ
thay đ i (n không đ i). Nh v y, giá tr c a bi u th c n ổ ổ ư ậ ị ủ ể ứ − p + d không thay đ i trongổ
su t quá trình ta b b t c nh c a G đ đ c m t cây. Cây này có n đ nh, do đó có n ố ỏ ớ ạ ủ ể ượ ộ ỉ − 1
c nh và cây ch có m t mi n, vì v y:ạ ỉ ộ ề ậ
n − p + d = n − (n −1) + 1 = 2.
H th c n ệ ứ − p + d = 2 th ng g i là “h th c Euler cho hình đa di n”, vì đ cườ ọ ệ ứ ệ ượ
Euler ch ng minh đ u tiên cho hình đa di n có n đ nh, p c nh và d m t. M i hình đaứ ầ ệ ỉ ạ ặ ỗ
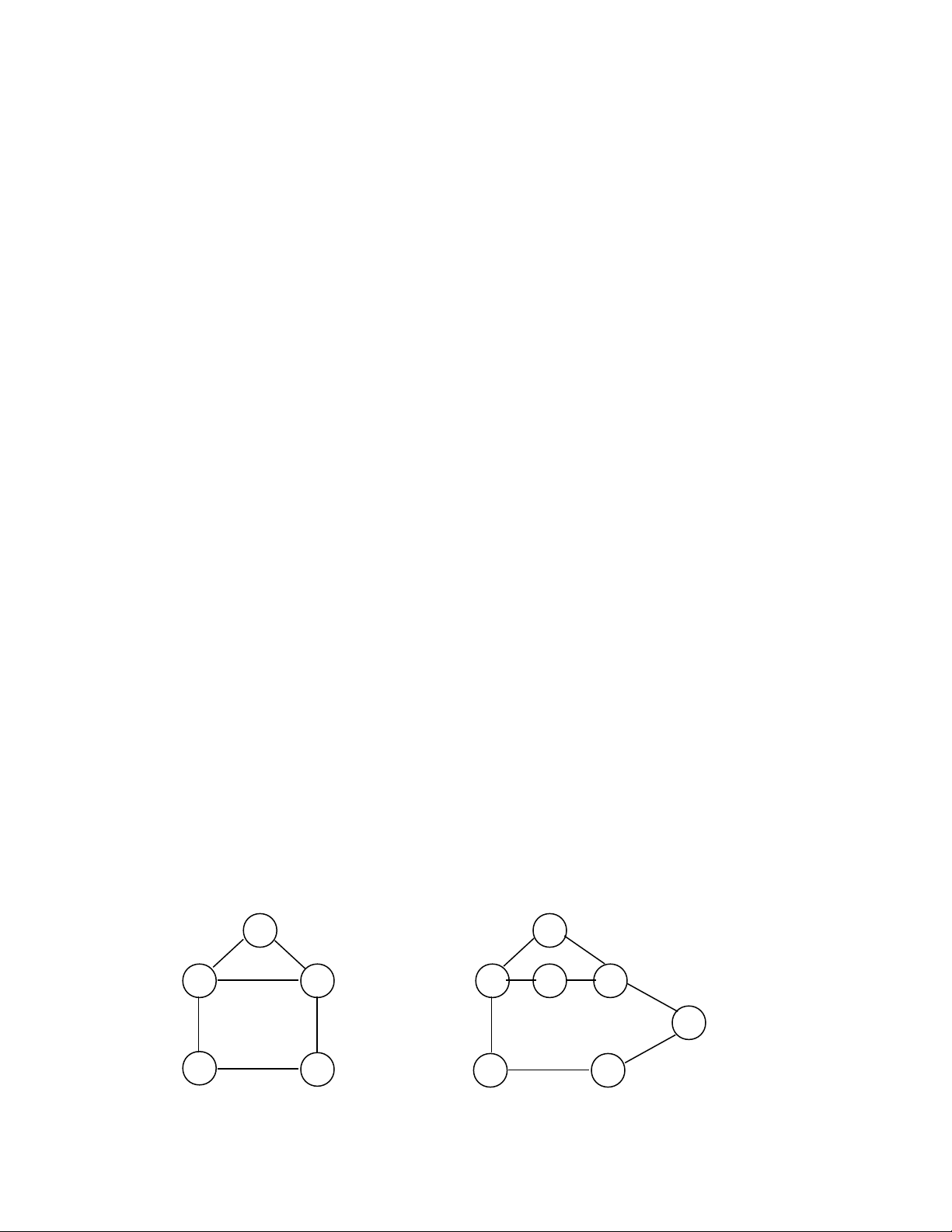
di n có th coi là m t đ th ph ng. Ch ng h n hình t di n ABCD và hình h pệ ể ộ ồ ị ẳ ẳ ạ ứ ệ ộ
ABCDA’B’C’D’ có th bi u di n b ng các đ th d i đây.ể ể ễ ằ ồ ị ướ
7.1.4. H qu :ệ ả Trong m t đ th ph ng liên thông tuỳ ý, luôn t n t i ít nh t m t đ nhộ ồ ị ẳ ồ ạ ấ ộ ỉ
có b c không v t quá 5.ậ ượ
105
c
d
b
gh
a
f
e
M1
M2
M3
M4
M5
A
D
B C
B
B’ C’
C
A
A’
D
D’
Ch ng minh:ứ Trong đ th ph ng m i mi n đ c bao b ng ít nh t 3 c nh. M t khác,ồ ị ẳ ỗ ề ượ ằ ấ ạ ặ
m i c nh có th n m trên biên c a t i đa hai mi n, nên ta có 3d ỗ ạ ể ằ ủ ố ề ≤ 2p.
N u trong đ th ph ng mà t t c các đ nh đ u có b c không nh h n 6 thì doế ồ ị ẳ ấ ả ỉ ề ậ ỏ ơ
m i đ nh c a đ th ph i là đ u mút c a ít nh t 6 c nh mà m i c nh l i có hai đ uỗ ỉ ủ ồ ị ả ầ ủ ấ ạ ỗ ạ ạ ầ
mút nên ta có 6n ≤ 2p hay 3n ≤ p. T đó suy ra 3d+3n ừ≤ 2p+p hay d+n ≤ p, trái v i hớ ệ
th c Euler d+n=p+2.ứ
7.2. Đ TH KHÔNG PH NG.Ồ Ị Ẳ
7.2.1. Đ nh lý:ị Đ th phân đôi đ y đ Kồ ị ầ ủ 3,3 là m t đ th không ph ng.ộ ồ ị ẳ
Ch ng minh:ứ Gi s Kả ử 3,3 là đ th ph ng. Khi đó ta có m t đ th ph ng v i 6 đ nhồ ị ẳ ộ ồ ị ẳ ớ ỉ
(n=6) và 9 c nh (p=9), nên theo Đ nh lý Euler đ th có s mi n là d=pạ ị ồ ị ố ề −n+2=5.
đây, mõi c nh chung cho hai mi n, mà m i mi n có ít nh t 4 c nh. Do đóỞ ạ ề ỗ ề ấ ạ
4d≤2p, t c là 4x5ứ≤2x9, vô lý.
Nh v y đ nh lý này cho ta l i gi i c a bài toán “Ba nhà ba gi ng”, nghĩa làư ậ ị ờ ả ủ ế
không th th c hi n đ c vi c làm các đ ng khác đ n gi ng sao cho các đ ng nàyể ự ệ ượ ệ ườ ế ế ườ
đôi m t không giao nhau.ộ
7.2.2. Đ nh lý:ị Đ th đ y đ Kồ ị ầ ủ 5 là m t đ th không ph ng.ộ ồ ị ẳ
Ch ng minh:ứ Gi s Kả ử 5 là đ th ph ng. Khi đó ta có m t đ th ph ng v i 5 đ nhồ ị ẳ ộ ồ ị ẳ ớ ỉ
(n=5) và 10 c nh (p=10), nên theo Đ nh lý Euler đ th có s mi n là d=pạ ị ồ ị ố ề −n+2=7.
Trong K5, m i mi n có ít nh t 3c nh, m i c nh chung cho hai mi n, vì v yỗ ề ấ ạ ỗ ạ ề ậ
3d≤2n, t c là 3x7ứ≤2x10, vô lý.
7.2.3. Chú ý: Ta đã th y Kấ3,3 và K5 là không ph ng. Rõ ràng, m t đ th là khôngẳ ộ ồ ị
ph ng n u nó ch a m t trong hai đ th này nh là đ th con. H n n a, t t c các đẳ ế ứ ộ ồ ị ư ồ ị ơ ữ ấ ả ồ
th không ph ng c n ph i ch a đ th con nh n đ c t Kị ẳ ầ ả ứ ồ ị ậ ượ ừ 3,3 ho c Kặ5 b ng m t sằ ộ ố
phép toán cho phép nào đó.
Cho đ th G, có c nh (u,v). N u ta xoá c nh (u,v), r i thêm đ nh w cùng v i haiồ ị ạ ế ạ ồ ỉ ớ
c nh (u,w) và (w,v) thì ta nói r ng ta đã thêm đ nh m i w (b c 2) đ t trên c nh (u,v)ạ ằ ỉ ớ ậ ặ ạ
c a G.ủ
Đ th G’ đ c g i là đ ng phôi v i đ th G n u G’ có đ c t G b ng cáchồ ị ượ ọ ồ ớ ồ ị ế ượ ừ ằ
thêm các đ nh m i (b c 2) đ t trên các c nh c a G.ỉ ớ ậ ặ ạ ủ
Thí d 3:ụ
G G’
106
a
u v
bc
a
u v w
b c
d
Đ th G là đ ng phôi v i đ th G’.ồ ị ồ ớ ồ ị
Nhà toán h c Ba Lan, Kuratowski, đã thi t l p đ nh lý sau đây vào năm 1930.ọ ế ậ ị
Đ nh lý này đã bi u th đ c đi m c a các đ th ph ng nh khái ni m đ th đ ngị ể ị ặ ể ủ ồ ị ẳ ờ ệ ồ ị ồ
phôi.
7.2.4. Đ nh lý (Kuratowski):ị Đ th là không ph ng khi và ch khi nó ch a m t đồ ị ẳ ỉ ứ ộ ồ
th con đ ng phôi v i Kị ồ ớ 3,3 ho c Kặ5.
Thí d 4:ụ
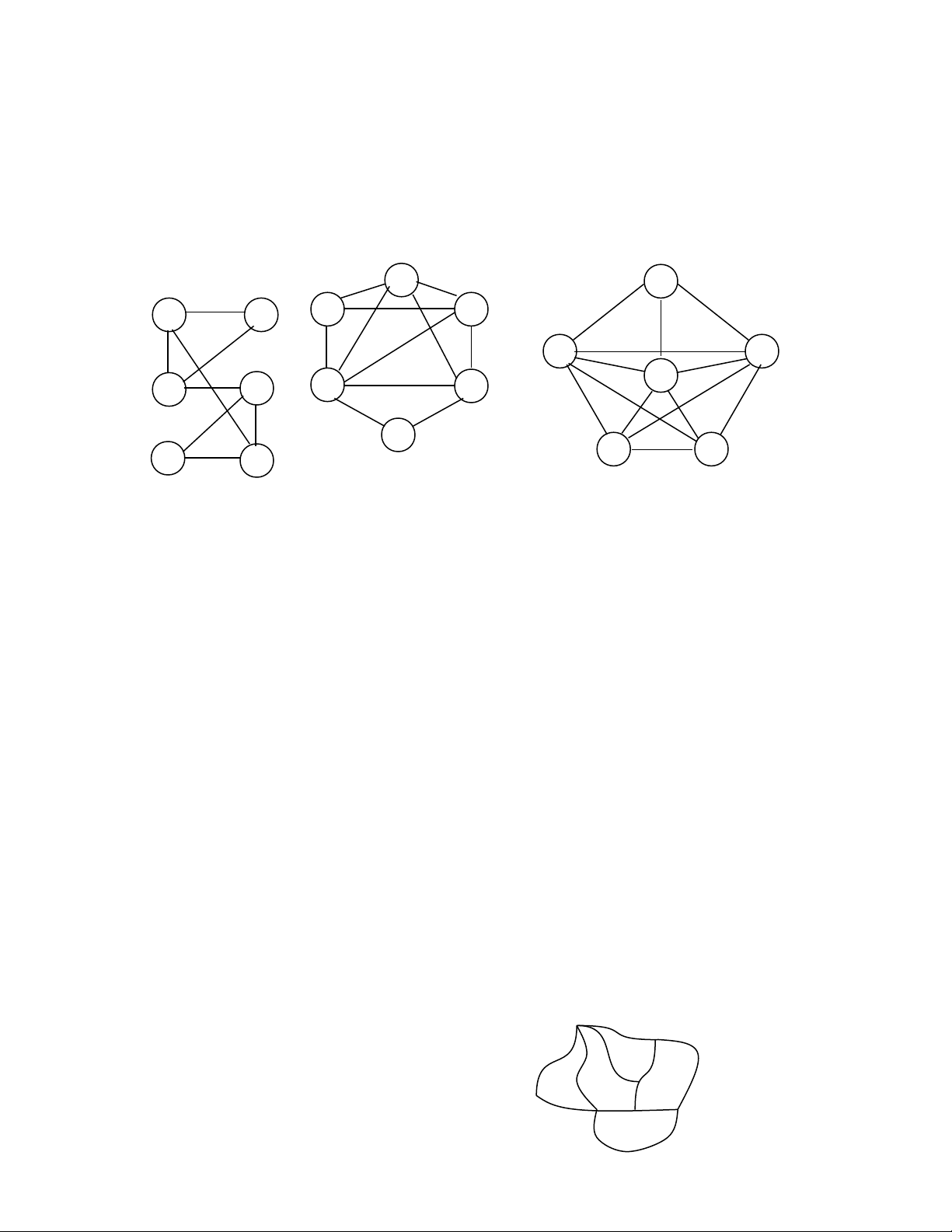
Hình 1 Hình 2 Hình 3
Đ th trong hình 1 và 2 là đ th ph ng. Các đ th này có 6 đ nh, nh ng khôngồ ị ồ ị ẳ ồ ị ỉ ư
ch a đ th con Kứ ồ ị 3,3 đ c vì có đ nh b c 2, trong khi t t c các đ nh c a Kượ ỉ ậ ấ ả ỉ ủ 3,3 đ u cóề
b c 3; cũng không th ch a đ th con Kậ ể ứ ồ ị 5 đ c vì có nh ng đ nh b c nh h n 4, trongượ ữ ỉ ậ ỏ ơ
khi t t c các đ nh c a Kấ ả ỉ ủ 5 đ u có b c 4.ề ậ
Đ th trong hình 3 là đ th không ph ng vì n u xoá đ nh b cùng các c nh (b,a),ồ ị ồ ị ẳ ế ỉ ạ
(b,c), (b,f) ta đ c đ th con là Kượ ồ ị 5.
7.3. TÔ MÀU Đ TH .Ồ Ị
7.3.1. Tô màu b n đ :ả ồ
M i b n đ có th coi là m t đ th ph ng. Trong m t b n đ , ta coi hai mi nỗ ả ồ ể ộ ồ ị ẳ ộ ả ồ ề
có chung nhau m t đ ng biên là hai mi n k nhau (hai mi n ch có chung nhau m tộ ườ ề ề ề ỉ ộ
đi m biên không đ c coi là k nhau). M t b n đ th ng đ c tô màu, sao cho haiể ượ ề ộ ả ồ ườ ượ
mi n k nhau đ c tô hai màu khác nhau. Ta g i m t cách tô màu b n đ nh v y làề ề ượ ọ ộ ả ồ ư ậ
m t cách tô màu đúng.ộ
Đ đ m b o ch c ch n hai mi n k nhau không bao gi có màu trùng nhau,ể ả ả ắ ắ ề ề ờ
chúng ta tô m i mi n b ng m t màu khác nhau. Tuy nhiên vi c làm đó nói chung làỗ ề ằ ộ ệ
không h p lý. N u b n đ có nhi u mi n thì s r t khó phân bi t nh ng màu g nợ ế ả ồ ề ề ẽ ấ ệ ữ ầ
gi ng nhau. Do v y ng i ta ch dùng m t s màu c n thi t đ tô b n đ . M t bàiố ậ ườ ỉ ộ ố ầ ế ể ả ồ ộ
toán đ c đ t ra là: xác đ nh s màu t i thi u c n có đ tô màu đúng m t b n đ .ượ ặ ị ố ố ể ầ ể ộ ả ồ
Thí d 5: ụB n đ trong hình bên có 6 mi n,ả ồ ề
nh ng ch c n có 3 màu (vàng, đ , xanh)ư ỉ ầ ỏ
đ tô đúng b n đ này. Ch ng h n, màu vàngể ả ồ ẳ ạ
đưc tô cho Mợ1 và M4, màu đ đ c tô cho Mỏ ượ 2
107
a b
cd
f
e
a c
b
fd
e
b
f c
e d
a
M1
M2
M3
M4
M5
M6
và M6, màu xanh đ c tô cho Mượ 3 và M5.
7.3.2. Tô màu đ th :ồ ị
M i b n đ trên m t ph ng có th bi u di n b ng m t đ th , trong đó m iỗ ả ồ ặ ẳ ể ể ễ ằ ộ ồ ị ỗ
mi n c a b n đ đ c bi u di n b ng m t đ nh; các c nh n i hai đ nh, n u các mi nề ủ ả ồ ượ ể ễ ằ ộ ỉ ạ ố ỉ ế ề
đ c bi u di n b ng hai đ nh này là k nhau. Đ th nh n đ c b ng cách này g i làượ ể ễ ằ ỉ ề ồ ị ậ ượ ằ ọ
đ th đ i ng u c a b n đ đang xét. Rõ ràng m i b n đ trên m t ph ng đ u có đồ ị ố ẫ ủ ả ồ ọ ả ồ ặ ẳ ề ồ
th đ i ng u ph ng. Bài toán tô màu các mi n c a b n đ là t ng đ ng v i bài toánị ố ẫ ẳ ề ủ ả ồ ươ ươ ớ
tô màu các đ nh c a đ th đ i ng u sao cho không có hai đ nh li n k nhau có cùngỉ ủ ồ ị ố ẫ ỉ ề ề
m t màu, mà ta g i là tô màu đúng các đ nh c a đ th .ộ ọ ỉ ủ ồ ị
S màu ít nh t c n dùng đ tô màu đúng đ th G đ c g i là s c s c a đ thố ấ ầ ể ồ ị ượ ọ ắ ố ủ ồ ị
G và ký hi u là χ(G).ệ
Thí d 6:ụ
Ta th y r ng 4 đ nh b, d, g, e đôi m t k nhau nên ph i đ c tô b ng 4 màuấ ằ ỉ ộ ề ả ượ ằ
khác nhau. Do đó χ(G) ≥ 4. Ngoài ra, có th dùng 4 màu đánh s 1, 2, 3, 4 đ tô màu Gể ố ể
nh sau:ư
Nh v y χ(G) = 4.ư ậ
7.3.3. M nh đ :ệ ề N u đ th G ch a m t đ th con đ ng phôi v i đ th đ y đ Kế ồ ị ứ ộ ồ ị ồ ớ ồ ị ầ ủ n
thì χ(G) ≥ n.
Ch ng minh:ứ G i H là đ th con c a G đ ng phôi v i Kọ ồ ị ủ ồ ớ n thì χ(H) ≥ n. Do đó χ(G) ≥ n.
7.3.4. M nh đ :ệ ề N u đ n đ th G không ch a chu trình đ dài l thì χ(G) =2.ế ơ ồ ị ứ ộ ẻ
Ch ng minh:ứ Không m t tính ch t t ng quát có th gi s G liên thông. C đ nh đ nhấ ấ ổ ể ả ử ố ị ỉ
u c a G và tô nó b ng màu 0 trong hai màu 0 và 1. V i m i đ nh v c a G, t n t i m tủ ằ ớ ỗ ỉ ủ ồ ạ ộ
đ ng đi t u đ n v, n u đ ng này có đ dài ch n thì tô màu 0 cho v, n u đ ng nàyườ ừ ế ế ườ ộ ẵ ế ườ
108
a b c
d e
f g h
312
2 4
4 3 1