Chương 2
Lý thuyết mặt
2.1 Mặt chính qui
Có thể hình dung mặt chính qui trong R3như sau: Lấy một số mảnh mặt phẳng biến dạng chúng
và “dán” lại sao cho hình nhận được không có các điểm nhọn, không có các cạnh hoặc không có
tính tự cắt để tại mỗi điểm có thể nói đến mặt phẳng tiếp xúc của mặt. Các mặt cũng sẽ được giả
thiết đủ trơn để có thể mở rộng các khái niệm cũng như các kết quả của giải tích lên chúng. Định
nghĩa sau đây thỏa mãn các yêu cầu trên.
Định nghĩa 1. Một tập hợp con S⊂R3được gọi là một mặt chính qui nếu ∀p∈Stồn tại lân
cận V⊂R3của pvà ánh xạ X:U−→ V∩S,vớiUlà một tập con mở của R2,thỏa mãn 3 điều
kiện sau:
1. Ánh xạ Xlà khả vi, có nghĩa là
X(u, v)=(x(u, v),y(u, v),z(u, v)),(u, v)∈U
với x, y, z là các hàm có đạo hàm riêng mọi cấp.
2. Ánh xạ Xlà một đồng phôi từ Uvào V∩S. Vì Xlà liên tục theo điều kiện 1, nên Xlà một
đồng phôi có nghĩa là Xcó ánh xạ ngược X−1:V∩S−→ Uliên tục. Nói cách khác, X−1là
hạn chế của một ánh xạ liên tục F:W⊂R3−→ R2xác định trên một tập mở chứa V∩S.
3. (Tính chính qui) Với mọi q∈U, đạo hàm DXq:R2−→ R3là một đơn ánh.
Ánh xạ Xđược gọi là một tham số hóa (địa phương) của S, cặp (U, X)gọi là một hệ tọa độ địa
phương hay một bản đồ của Scòn lân cận V∩Scủa ptrong Sgọi là một lân cận tọa độ.
1
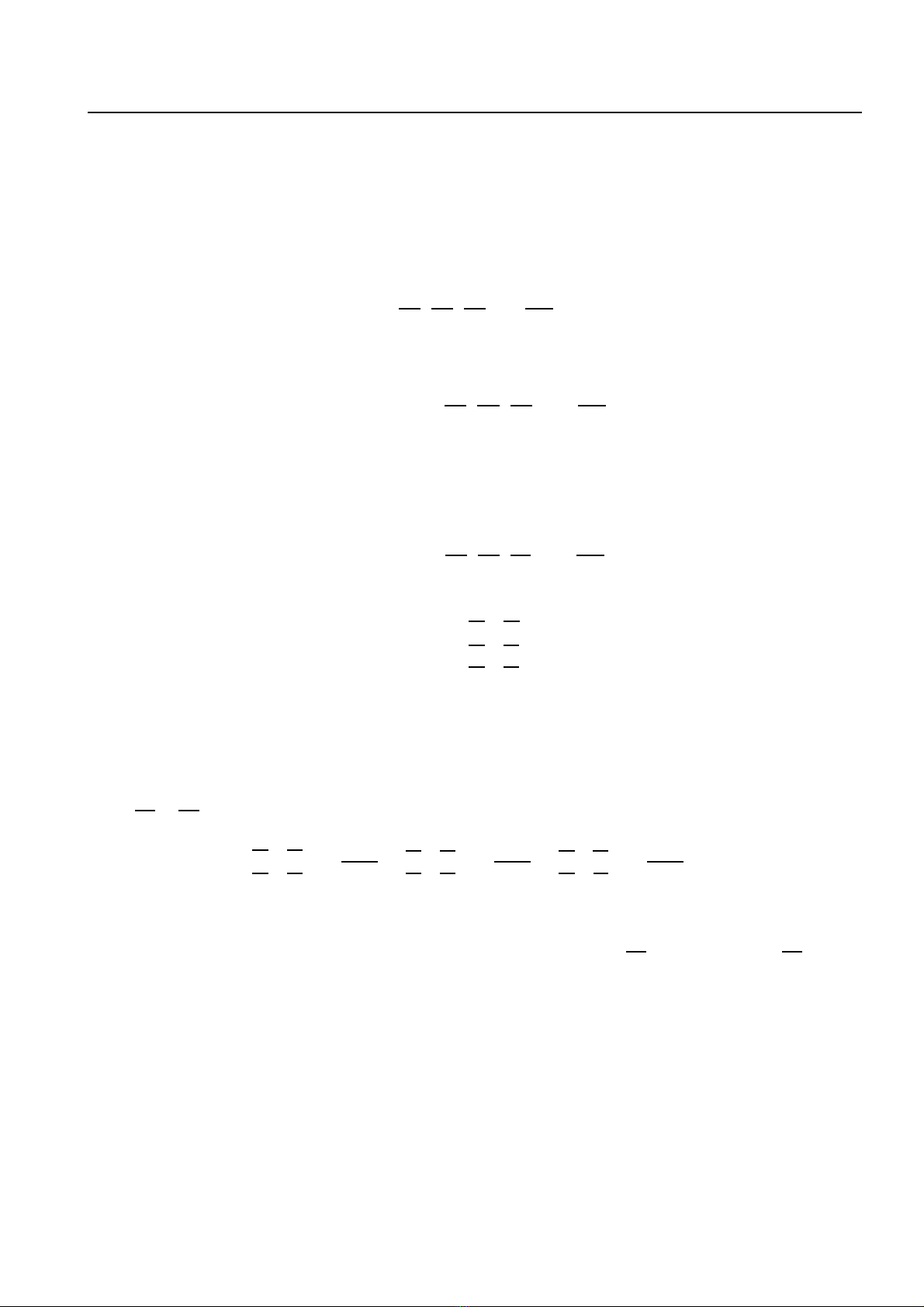
Hình học vi phân (Giáo trình đang chỉnh lý. Version 1)
Chúng ta phân tích rõ hơn về Điều kiện 3 bằng cách xét ma trận Jacobi của Xtại q. Giả sử
q=(u0,v
0).Xét đường tham số
u7−→ (x(u, v0),y(u, v0),z(u, v0)).
Đường cong này, được gọi là đường cong tọa độ v=v0,nằm trên mặt Sđi qua p=X(q)và có
vector tiếp xúc tại plà
(∂x
∂u,∂y
∂u,∂z
∂u):=∂X
∂u .
Ở đây các đạo hàm riêng được tính tại q=(u0,v
0).Theo định nghĩa của đạo hàm ta có
DXq(e1)=∂x
∂u,∂y
∂u,∂z
∂u:= ∂X
∂u ,
với e1là vector tiếp xúc của đường tham số u7−→ (u, v0)trong R2tại điểm q. Đường tọa độ v=v0
là ảnh của đường cong này qua ánh xạ X. Tương tự ta có e2là vector tiếp xúc của đường tham
số v7−→ (u0,v)trong R2tại điểm q. Đường tọa độ u=u0là ảnh của đường cong này qua ánh xạ
Xvà
DXq(e2)=∂x
∂v,∂y
∂v,∂z
∂v:= ∂X
∂v .
Ta có ma trận Jacobi
X′
q=
∂x
∂u
∂x
∂v
∂y
∂u
∂y
∂v
∂z
∂u
∂z
∂v
.
Với phân tích này ta thấy Điều kiện 3 tương đương với các một trong các điều kiện sau:
1. hai cột của ma trận X′
qlà độc lập;
2. ∂X
∂u ∧∂X
∂v 6=0;
3. các định thức
∂x
∂u
∂x
∂v
∂y
∂u
∂y
∂v
:= ∂(x,y)
∂(u,v),
∂x
∂u
∂x
∂v
∂z
∂u
∂z
∂v
:= ∂(x,z)
∂(u,v),
∂y
∂u
∂y
∂v
∂z
∂u
∂z
∂v
:= ∂(y,z)
∂(u,v)không đồng thời bằng
không.
Từ đây về sau, để thuận tiện, đôi lúc chúng ta sẽ viết Xuthay cho ∂X
∂u và Xvthay cho ∂X
∂v .
Nhận xét 1. 1. Như vậy có thể xem mặt chính qui được phủ bởi một họ các lân cận tọa độ,
tức là các ảnh của một họ ánh xạ X(tham số hóa) thỏa mãn các Điều kiện 1, 2, 3.
2. Điều kiện 1 cho phép chúng ta có thể sử dụng công cụ của giải tích (phép tính vi tích phân)
để nghiên cứu các mặt chính qui.
2
Hình học vi phân (Giáo trình đang chỉnh lý. Version 1)
3. Điều kiện 2 nhằm ngăn cản tính tự cắt của mặt và do đó có thể nói đến mặt phẳng tiếp xúc
của mặt tại mọi điểm.
4. Điều kiện 3 đảm bảo tại mọi điểm đều có mặt phẳng tiếp xúc.
Ví dụ 1. Xét mặt phẳng R2.Ta chọn U=R2và X=Id. Theo định nghĩa R2là mặt chính qui
với chỉ một bản đồ duy nhất (R2,Id).
Ví dụ 2. Xét mặt cầu
S2={(x, y, z)∈R3:x2+y2+z2=1}.
Chúng ta sẽ chứng tỏ S2là một mặt chính qui. Xét ánh xạ X1:U+
1⊂R2−→ R3được cho bởi
X+
1(x, y)=(x, y, p1−x2−y2),(x, y)∈U+
1
với R2={(x, y, z)∈R3:z=0},U
+
1={(x, y)∈R2:x2+y2<1}và X+
1(U+
1)={(x, y, z)∈R3:
x2+y2+z2=1;z>0}là nửa mặt cầu trên. Do x2+y2<1nên hàm p1−x2−y2có các đạo
hàm riêng liên tục mọi cấp. Do đó Điều kiện 1 được thỏa mãn.
Dễ thấy X+
1là đơn ánh và (X+
1)−1là hạn chế của phép chiếu π(x, y, z)=(x, y)từ R3lên R2nên
cũng liên tục. Vậy Điều kiện 2 cũng được thỏa mãn.
Do ∂(x, y)
∂(x, y)=
10
01
=1nên Điều kiện 3 cũng được thỏa mãn. Như vậy X+
1là một tham số hóa
của S2.Có thể dễ dàng nhận thấy S2được phủ bởi 6 mảnh lân cận tọa độ được xác định tương
tự như vậy. Bạn đọc có thể dễ dàng xác định lân cận tọa độ tương ứng của các tham số hóa như
vậy. Dưới đây là các tham số hóa đó
X−
1(x, y)=(x, y, −p1−x2−y2),(x, y)∈U−
1={(x, y)∈R2:x2+y2<1};
X+
2(x, z)= (x, √1−x2−z2,z),(x, z)∈U+
2={(x, z)∈R2:x2+z2<1};
X−
2(x, z)=(x, −√1−x2−z2,z),(x, z)∈U−
2={(x, z)∈R2:x2+z2<1};
X+
3(y, z)= (
p1−y2−z2,y,z),(y, z)∈U+
3={(y, z)∈R2:y2+z2<1};
X−
3(y, z)=(−p1−y2−z2,y,z),(y, z)∈U−
3={(y, z)∈R2:y2+z2<1}.
Thường để dễ khảo sát mặt cầu S2, người ta sử dụng hệ tọa độ cầu để tham số hóa.
Lấy V={(θ, ϕ):0<θ<π, 0<ϕ<2π}và xét X:V−→ R3xác định bởi
X(θ, ϕ) = (sin θcos ϕ, sin θsin ϕ, cos θ).
Dễ thấy X(V)⊂S2.Tham số θđược gọi là colatude (phần phụ của vĩ độ) và ϕlà kinh độ. Rõ
ràng Xkhả vi vì các hàm sin θcos ϕ, sin θsin ϕ, cos θlà khả vi.
Hơn nữa các định thức
∂(x, y)
∂(θ, ϕ)= cos θsin θ, ∂(x, z)
∂(θ, ϕ)= sin2θsin ϕ, ∂(y, z)
∂(θ, ϕ)= sin2θcos ϕ
3
Hình học vi phân (Giáo trình đang chỉnh lý. Version 1)
không thể đồng thời bằng không vì
cos2θsin2θ+ sin4θsin2ϕ+ sin4θcos2ϕ= sin2θ6=0
do 0<θ<π.Như vậy, Điều kiện 1 và 3 được thỏa mãn. Lấy Clà nửa đường tròn
{(x, y, z)∈S2:y=0,x≥0}.
Với mỗi (x, y, z)∈S2−C, chúng ta xác định được duy nhất θ= cos−1zvì 0<θ<π.Biết θ
chúng ta sẽ xác định được ϕtừ x= sin θcos ϕ, y = sin θsin ϕvà do đó xác định được duy nhất ϕ.
Vậy Xcó ánh xạ ngược X−1,và có thể kiểm tra dễ dàng X−1là liên tục, tức là Xlà một tham
số hóa. Chúng ta nhận xét rằng X(V)=S2−Cnên có thể phủ S2bởi hai tham số hóa kiểu như
trên.
Cũng có thể phủ S2bởi hai lân cận tọa độ nhờ vào phép chiếu nổi (xem bài tập ??).
Ví dụ vừa rồi cho thấy việc kiểm tra một tập nào đó là một mặt chính chính qui là một công việc
dễ chán và buồn tẻ. Những mệnh đề tiếp theo sẽ cho ta những phương pháp có thể kiểm tra hoặc
xây dựng một số mặt chính qui dễ dàng hơn.
Mệnh đề 2.1.1. Nếu f:U−→ Rlà hàm khả vi trên tập mở U⊂R2.Khi đó đồ thị của f
Gf={(x, y, z)∈R3:z=f(x, y)}
là một mặt chính qui.
Chứng minh. Điều kiện 1 hiển nhiên được thỏa mãn. Do ∂(x,y)
∂(x,y)=1,nên Điều kiện 3 cũng được
thỏa mãn. Chúng ta chỉ còn chứng minh cho Điều kiện 2. Dễ thấy X(x, y)=(x, y, f(x, y)) là đơn
ánh nên có ánh xạ ngược X−1.Ánh xạ ngược X−1chính là hạn chế lên Gfcủa phép chiếu từ R3
lên R2nên liên tục. ✷
Định nghĩa 2. Cho ánh xạ khả vi f:U⊂Rn−→ Rm,với Ulà tập mở. Chúng ta nói rằng p∈U
là một điểm tới hạn của fnếu đạo hàm Dfp:Rn−→ Rmkhông phải là toàn ánh. Ảnh f(p)∈Rm
của một điểm tới hạn gọi là giá trị tới hạn của f. Một điểm của Rmmà không phải là giá trị tới
hạn được gọi là một giá trị chính qui của f.
Chú ý rằng bất kỳ điểm a6∈ F(U)đều là các giá trị chính qui của F.
Trong trường hợp f:U⊂R−→ R,các điểm tới hạn chính là các điểm x∈Umà f′(x)=0.
Nếu f:U⊂R3−→ Rlà hàm khả vi, ta có
f′(p)=∂f
∂x(p),∂f
∂y(p),∂f
∂z(p).
4
Hình học vi phân (Giáo trình đang chỉnh lý. Version 1)
Tính chất Dfpkhông là toàn ánh tương đương với
∂f
∂x(p)=∂f
∂y(p)=∂f
∂z (p)=0.
Do đó, nếu alà giá trị chính qui thì ∂f
∂x,∂f
∂y ,∂f
∂z không đồng thời triệt tiêu trên tập
f−1(a)={(x, y, z)∈R3:f(x, y, z)=a}.
Mệnh đề 2.1.2. Nếu f:U⊂R3−→ R,là hàm khả vi và a∈f(U)là giá trị chính qui của fthì
f−1(a),nếu khác rỗng, là một mặt chính qui trong R3.
Chứng minh. Lấy p=(x0,y
0,z
0)∈f−1(a).Vì alà giá trị chính qui nên không mất tính tổng
quát ta có thể giả sử ∂f
∂z (p)6=0. Đặt F:U⊂R3−→ R3xác định bởi
F(x, y, z)=(x, y, f(x, y, z)).
Ta có
F′
p=
100
010
fxfyfz
.
Do |F′
p|=∂f
∂z (p)6=0,nên theo Định lý hàm ngược, tồn tại lân cận Vcủa pvà Wcủa a=f(p)
sao cho F:V−→ Wlà một vi phôi. Điều này cho thấy các hàm tọa độ của F−1có dạng
x=u, y =v, z =g(u, v, t),(u, v, t)∈W
là các hàm khả vi. Đặc biệt z=g(u, v, a)=h(x, y)là hàm khả vi xác định trong hình chiếu của
Vlên mặt phẳng xy. Do
F(f−1(a)∩V)=W∩{(u, v, t)∈R3:t=a},
chúng ta suy ra rằng đồ thị của hlà f−1(a)∩V. Theo Mệnh đề 2.1.1, f−1(a)∩Vlà một lân cận
tọa độ chứa p. Do đó, f−1(a)sẽ được phủ bởi những lân cận tọa độ như vậy nên f−1(a)là một
mặt chính qui. ✷
Ví dụ 3. Ellipsoid E
x2
a2+y2
b2+z2
c2=1
là một mặt chính qui. Echính là tập f−1(0),với
f(x, y, z)= x2
a2+y2
b2+z2
c2−1
5