Hướng dẫn giải đề thi tuyển sinh Đại học năm 2014
Môn – Khối
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 1 -
HƯỚNG DẪN GIẢI ĐỀ THI TUYỂN SINH ĐẠI HỌC NĂM 2014
MÔN: TOÁN - KHỐI A, A1
Câu 1.
a. Khảo sát hàm số
Khảo sát và vẽ đồ thị hàm số y =
2
1
x
x
1. Tập xác định: D = (-
; 1) U (1; +
)
2. Sự biến thiên
a) Đạo hàm
y' =
2
1 .1 2 .1
1
xx
x
y' = 0 <=> vô nghiệm, hàm số không có cực trị
b) Giới hạn và các đường tiệm cận
+ Ta có
lim y (x=>1-) = -
lim y (x=>1+) = +
=> đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số đã cho
+ Giới hạn tại vô cực
lim y (x=>+
) = 1
lim y (x=>-
) = 1
=> đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số đã cho
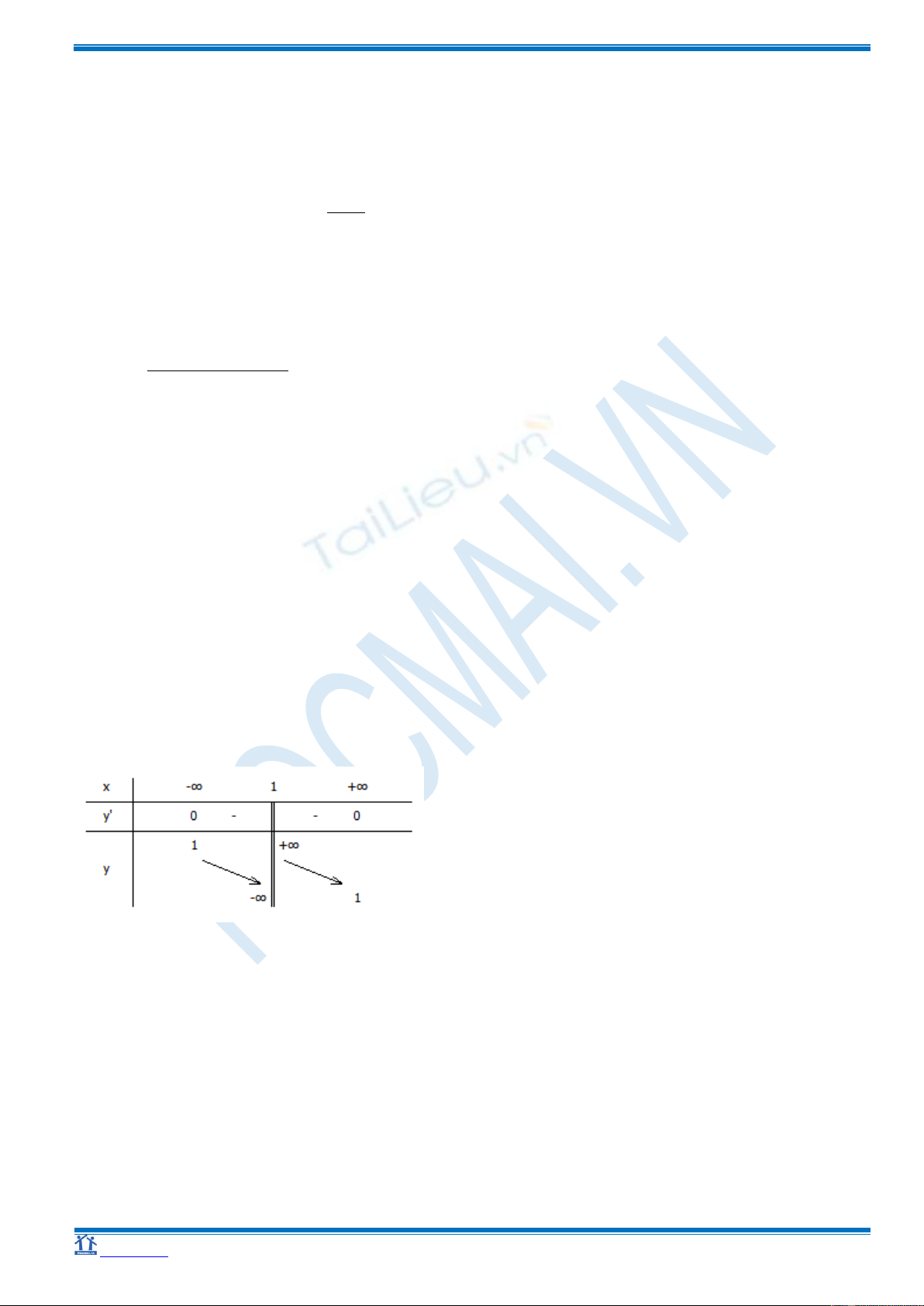
c) Bảng biến thiên
d) Chiều biến thiên và các cực trị
+ Hàm số nghịch biến trên ( -
; 1 )
+ Hàm số nghịch biến trên ( 1 ; +
)
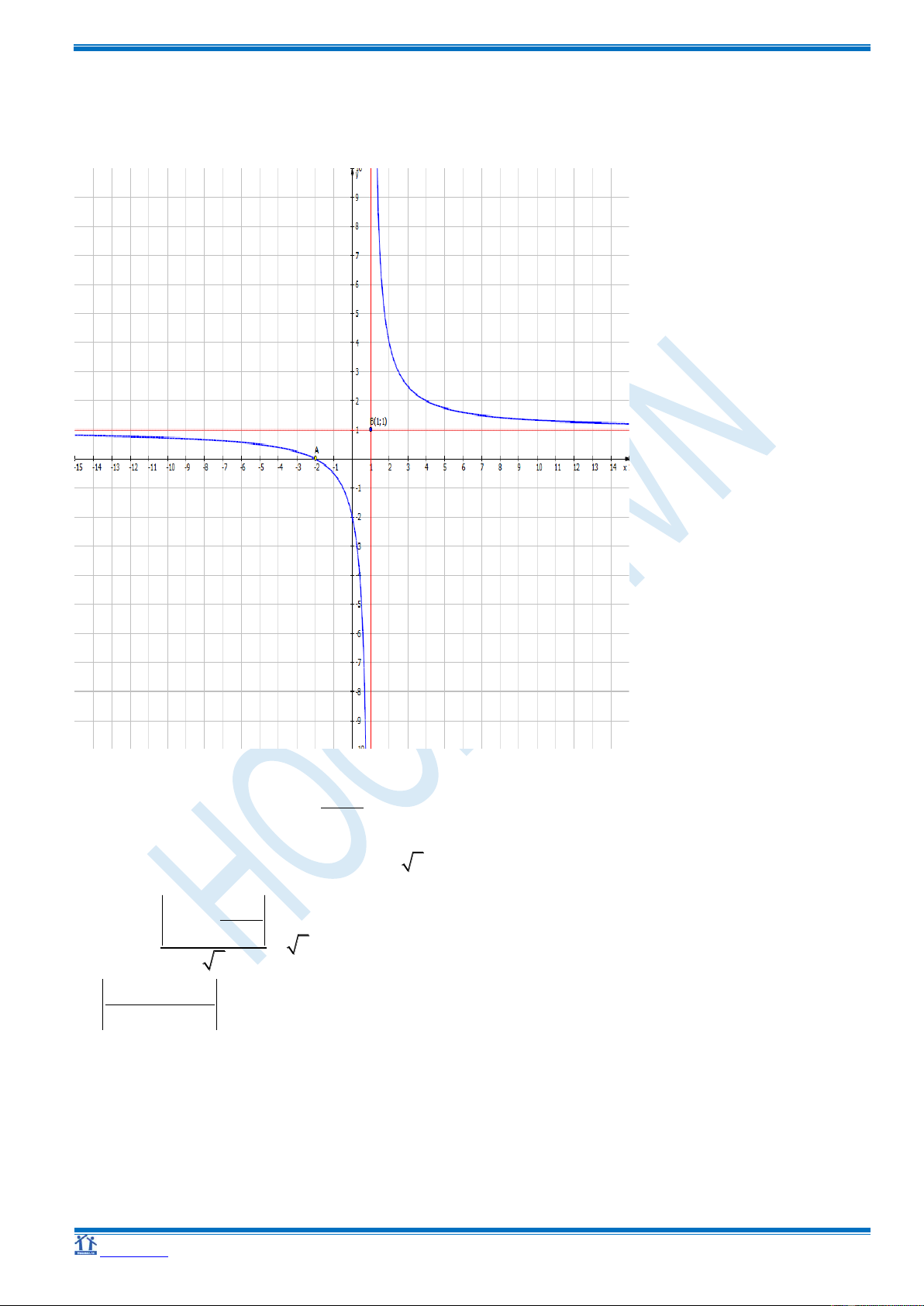
3. Đồ thị
a) Giao điểm của đồ thị hàm số với hệ toạ độ
+ Giao điểm của hàm số đối với trục Ox
y = 0 <=> x = -2
+ Giao điểm của hàm số đối với trục Oy
x = 0 <=> y = -2
Hướng dẫn giải đề thi tuyển sinh Đại học năm 2014
Môn – Khối
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 2 -
b) Nhận xét
+ Đồ thị hàm số nhận giao điểm B (1;1) của 2 tiệm cận làm tâm đối xứng
c) Vẽ đồ thị hàm số
b.
Vì M
C
nên ta có
0
0
0
3
1, x
Mx x
Ta có khoảng cách từ M đến
yx
là
2
0
00
,
2
0 0 0
0
22
0 0 0 0
22
0 0 0 0 0
0
0
3
1
2
2
32
2 3 2 3 0 ( )
2 3 2 4 3 0
1
3
M
x
xx
d
x x x
x
x x x x vong
x x x x x
x
x
Với
01 0; 2xM

Hướng dẫn giải đề thi tuyển sinh Đại học năm 2014
Môn – Khối
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 3 -
Với
03 2;0xM
Vậy có 2 điểm M thoả mãn yêu cầu bài toán M(0;-2), M(-2;0)
Câu 2
s inx 4 cos x 2 sin 2x.
sinx + 4cosx 2 2sin x cos x.
sinx 2 2 cos x(s inx 2).
sinx 2 (lo¹i)
1
cosx 2
1
cosx k2 (k )
23
Câu 3: Xét phương trình
2x1
x x 3 2x 1 x2
.
Vậy diện tích hình phẳng cần tính
là
22
2 2 3 2
11
2
11
S (2x 1) (x x 3) dx x 3x 2 dx ( x 3x 2x) 1
36
Câu 4.
a.Giả sử số phức
z a bi
(a,b thuộc R)
z a bi
.
Theo bài ra, ta có
2
z (2 i)z 3 5i
a bi (2 i)(a bi) 5i 3
a bi 2a 2bi ai bi 5i 3
a bi 2a 2bi ai b 5i 3
3a b i(a b) 3i 3
3a b 3
a b 5
a2
b3
Vậy số phức phần thực là 2 và phần ảo là -3
b. Số cách chọn 4 thẻ trong 16 thẻ là:
4
16
C
Gọi A = “4 thẻ được chọn đều được đánh số chẵn”
Ta có:
Từ 1 đến 16 tập các số chẵn là: {2,4,6,8,10,12,14,16}
=> Có 8 số chẵn
=> Số cách chọn để cả 4 thẻ đều là số chẵn là
4
8
C
=> Xác suất để 4 thẻ được chọn đều được đánh số chẵn là:
4
8
4
16
1
26
C
C
Câu 5. (P) 2x + y – 2z – 1= 0
(d)
23
1 2 3
x y z
Giao điểm d và (P) là nghiệm của hệ:
Hướng dẫn giải đề thi tuyển sinh Đại học năm 2014
Môn – Khối
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 4 -
2 2 1
2 2 1 0 20
23
3 2 6 0
1 2 3
x y z
x y z
xyy
x y z
yz
2 2 1 7 / 2
23
3 2 6 3/ 2
x y z x
x y y y
y z z
()
(1; 2;3); (2;1; 2)
dP
un
=>
()
2 3 3 1 1 2
, , , (1,8,5)
1 2 2 2 2 1
dP
un
Vecto pháp tuyến của mặt phẳng cần tìm là (1,8,5)
=> Mặt phẳng cần tìm là (
73
( ) 8.( 3) 5.( ) 0
22
x y z
=> x+8y+5z+13=0.
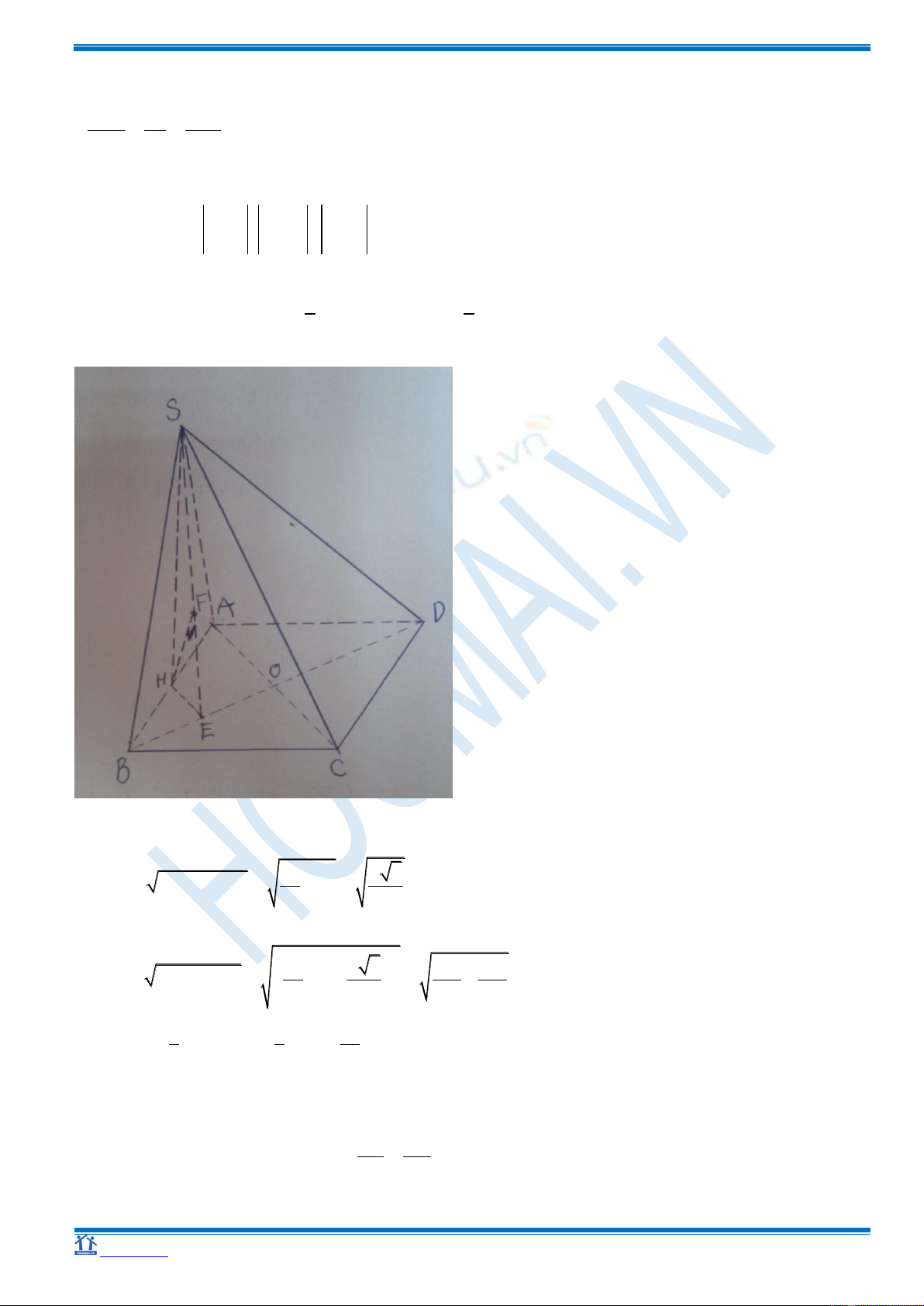
Câu 6
Gọi H là hình chiếu của S lên ABCD.
Ta có ∆ AHD vuông tại A
2
2 2 2 5
42
aa
HD AH AD a
Xét ∆ SHD vuông tại H
2
222
223 5 9 5
2 2 4 4
a a a a
SH SD HD a
3
2
.11
. . . .
3 3 3
S ABCD ABCD
a
V SH S a a
(đvtt)
b. Ta có: AB = 2AH
( ,( )) 2 ( ,( ))d A SBD d H SBD
Từ H kẻ
HE ( )
HE//AC => BD (SHE) (SHE) (SBD)
() 24
BD do BD AC
OB BD
E BD EB EO
Từ H kẻ HF
SE (F
SE) =>
( ) ( ,( ))HF SBD hay HF d H SBD

Hướng dẫn giải đề thi tuyển sinh Đại học năm 2014
Môn – Khối
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 5 -
Xét ∆ABO có HE là đường trung bình
222
AO a
HE
Xét ∆ vuông SHE vuông tại H:
2 2 2 2 2 2
1 1 1 1 8 9 2
( ,( ))
33
aa
HF d H SBD
HF HS HE a a a
Câu 7
Gọi độ dài cạnh hình vuông là m. E là hình chiếu vuông góc của M lên CD.
Gọi F là giao điểm của MN và CD, theo định lí Talet ta có :
FC NC NF 1
MA NA MN 3.
Ta có:
NM 3NF.
Gọi
F(x,y)
, ta có:
7
1 2 3(x 2) x7
F( ;0)
3
2 ( 1) 3(y 1) 3
y0
.
Mặt khác:
2
2 2 2
MA 1 m m 16 26
3 FC m EF mà ME = m MF m 4 m
FC 6 3 9 4 5
Khi đó ta có
EF 1
osMFD MF 10
c
Gọi VTPT của CD là
;
CD
n a b
, ta có: phương trình CD:
720
3
a x b y
và
3;1
MN
n
Mặt khác:
22
22
0
31
os CD,MF 9 6 43
10
. 10
a
ab
c a a ab ab
ab
Với a = 0 chon b = 1 ta có: CD: y = -2
Với 4a = -3b chọn a=3 và b=-4 ta có: CD: 3x – 4y -15 = 0
Vậy phương trình đường thẳng CD là: y = - 2 hoặc 3x – 4y – 15 = 0
Câu 8
) 2 12
12
y
x
2
2
22
2 2 2
2
2
12 12 12
12 12 12
12 144 24 12 12
12 144 24 12 12
12 24 12 12 12 0
12 0 ( )
12
24
12 12 0
12 12
1
12
x y y x
y x x y
y x y x y x y
y x y x y x x y
x x y y
y x loai
y
x
yy
x
y


























