Người soạn: NGUYỄN NGỌC MAI KHANH Bộ Môn Kỹ Thuật Điện Tử
Trang 7.1
Chương 7: KHUẾCH ĐẠI HỒI TIẾP ÂM VÀ
DAO ĐỘNG SIN
Có hai dạng mạch hồi tiếp. Thứ nhất là hồi tiếp âm: một phần hay toàn bộ tín hiệu ngõ ra
(điện áp hoặc dòng điện) được đưa về trở lại ngõ vào để có thể được trừ bởi tín hiệu ngõ
vào. Theo cách này, tín hiệu ngõ vào đến bộ khuếch đại đầu tiên được giảm xuống, như
vậy tín hiệu ngõ ra được giảm xuống cho phù hợp. Khuếch đại hồi tiếp âm được đặc điểm
là có hệ số khuếch đại thấp hơn bộ khuếch đại tương tự không có hồi tiếp.
Dạng thứ hai là hồi tiếp dương: một phần hay toàn bộ tín hiệu ngõ ra được đưa đến ngõ
vào để cộng thêm vào nó. Hồi tiếp dương thì không có ai muốn trong khuếch đại cả bởi
vì nó thường gây ra khuyếch đại không an toàn và dao động. Tuy nhiên tính chất này
được sử dùng nhiều trong mạch dao động. Trong chương này chúng ta chỉ đề cập đến
khuếch đại hồi tiếp âm.
7.1 Những khái niệm tổng quát về hồi tiếp
Hồi tiếp là công cụ vô cùng hữu ích trong rất nhiều ứng dụng, đặc biệt trong hệ thống
điều khiển. Hệ thống điều khiển bao gồm tất cả các mạch điện ở đó ngõ ra được sử dụng
để điều khiển hoặc hiệu chỉnh ngõ vào, từ đó lại cung cấp 1 ngõ ra như mong muốn. Sử
dụng khác của hồi tiếp là “cảm nhận” ngõ ra, sau đó so sánh nó với những tín hiệu khác,
và cuối cùng là điều khiển ngõ vào (và như ngõ ra) cho phù hợp với sự khác nhau giữa
tín hiệu ngõ vào và tín hiệu tham chiếu. Đặc biệt hồi tiếp âm trong sự khuyếch đại có thể
được sử dụng để:
1. Ổn định hệ số khuếch đại (điện áp hay dòng điện).
Hình 7.1 : Sơ đồ khối mạch khuếch đại hồi tiếp
2. Đạt được phép tuyến tính.
3. Làm rộng băng thông.
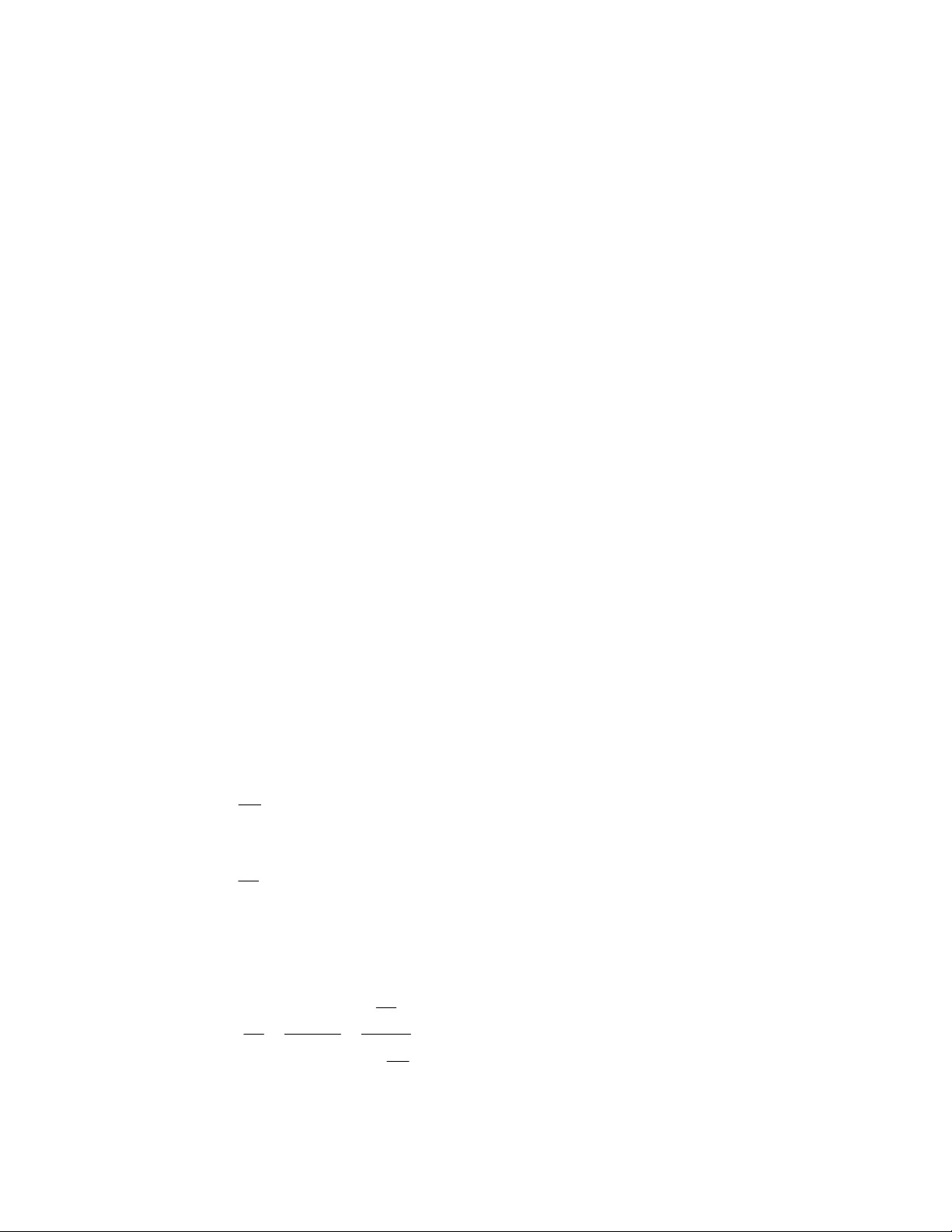
Người soạn: NGUYỄN NGỌC MAI KHANH Bộ Môn Kỹ Thuật Điện Tử
Trang 7.2
4. Giảm hoặc tăng trở kháng ngõ vào.
5. Giảm hoặc tăng trở kháng ngõ ra.
6. Giảm nhiễu trong bộ khuếch đại.
7. Làm giảm các hiệu ứng nhiệt.
Để ổn định hệ số khuếch đại, nghĩa là chúng ta muốn làm hệ số khuếch đại ít phụ thuộc
vào những thông số đặc biệt của thiết bị. Sự tuyến tính thì rất quan trọng cho bộ khuếch
đại, nhưng sự cải tiến tính tuyến tính (làm méo ít) này lại càng quan trọng hơn trong
khuếch đại công suất. Nhiễu ( tín hiệu điện giả được tạo ra không có khuếch đại ) đặc biệt
phiền toái trong khuếch đại khi mức tín hiệu hết sức nhỏ. Trong những trường hợp này,
hồi tiếp âm có thể được sử dụng làm giảm nhiễu trong bộ khuyếch đại.
Chúng ta sẽ phân loại kiểu của hồi tiếp theo hoạt động của hồi tiếp độ lợi. Hai kiểu đó là
mạch hồi tiếp dòng và mạch hồi tiếp áp, chúng được phân biệt bởi sự suy giảm độ lợi.
Hai kiểu hồi tiếp khác, giới hạn mạch Shunt và mạch hồi tiếp liên tục, cũng sẽ được xét.
Sơ đồ khối mạch khuếch đại hồi tiếp cơ bản như ở hình 7.1, với đường tín hiệu trên hình
vẽ. Tín hiệu ở bất kì điểm nào trong hình 7.1 cũng có thể là một điện áp hoặc dòng điện,
phụ thuộc vào dạng mong muốn.
7.2 KHUẾCH ĐẠI HỒI TIẾP ÁP
Xem hình 7.1, chúng ta thấy rằng khi toàn bộ tín hiệu là điện áp, mạch điện là một bộ
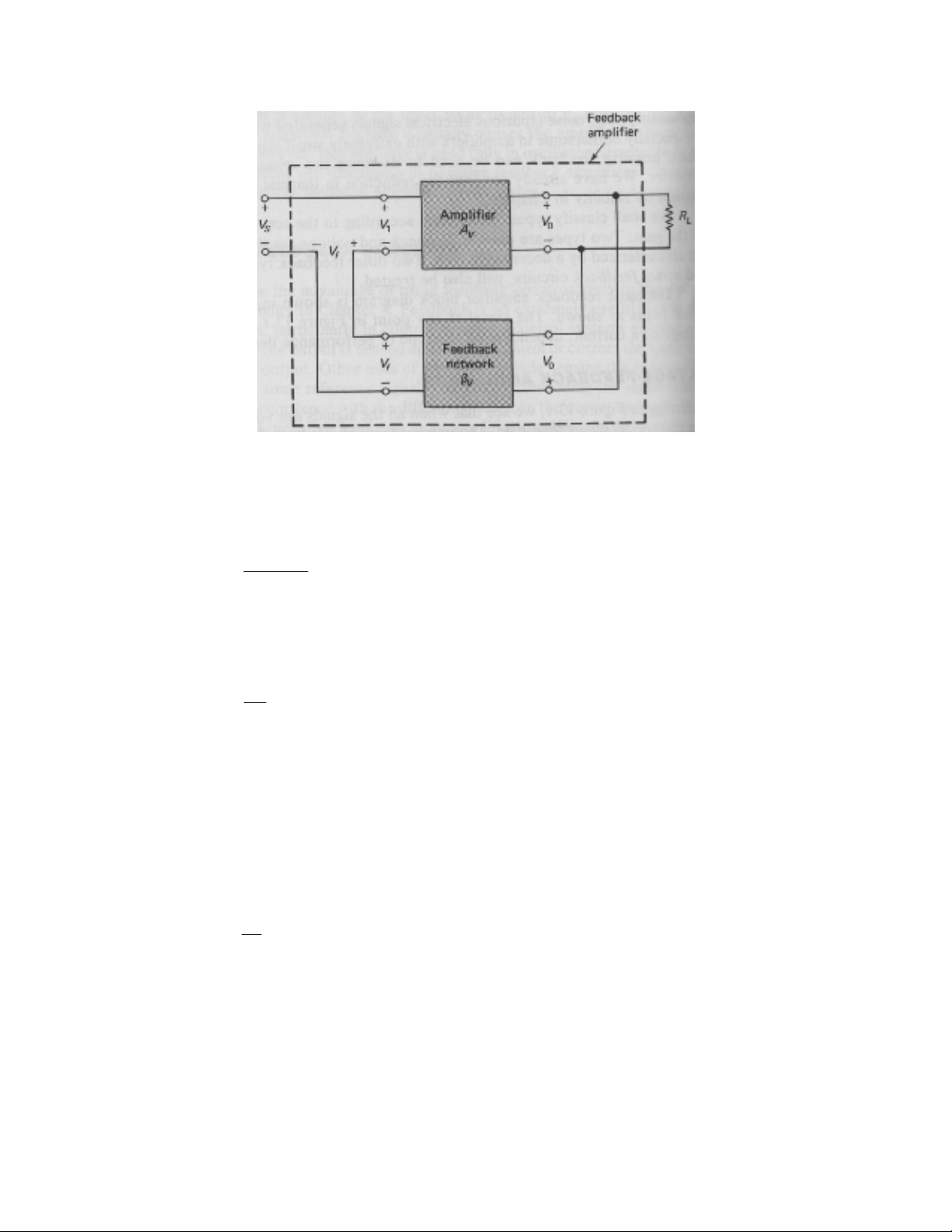
khuếch đại hồi tiếp áp. Dạng chung của khuếch đại hồi tiếp áp được thể hiện ở hình 7.2.
Hồi tiếp âm được thiết lập bằng cách lấy một phần của điện áp ngõ ra đưa về trừ cho điện
áp ngõ vào.
7.2.1 Độ lợi áp
Trong hình 7.2, điện áp ngõ ra xuất hiện qua cả tải bên ngoài và hệ thống hồi tiếp. Hệ
thống hồi tiếp điện áp ngược được định nghĩa:
o
f
vV
V
=
β
(7.1 )
Khuếch đại độ lợi áp mạch hở Av được định nghĩa.
1
V
V
Ao
v= (7.2)
Điện áp tổng ở ngõ vào đều bằng 0 được chỉ rõ hình 7.2. Chúng ta tìm được:
fs VVV += 1 (7.3)
Độ lợi dòng hở của khuếch đại hồi tiếp Avf được cho bởi
1
1
11V
V
V
V
VV
V
V
V
A
f
o
f
o
s
o
vf
+
=
+
== (7.4)
Người soạn: NGUYỄN NGỌC MAI KHANH Bộ Môn Kỹ Thuật Điện Tử
Trang 7.3
Hình 7.2 : Sơ đồ khối mạch khuếch đại hồi tiếp áp
Từ biểu thức (7.1) chúng ta thấy rằng Vf = ovV
β
. Cũng chú ý rằng Av = Vo/V1, chúng ta
tìm được
vv
v
vf A
A
A
β
+
=1 (7.5)
Chúng ta định nghĩa hồi tiếp âm cho ( 1 + vv A
β
) là lớn hơn 1 và hồi tiếp dương cho ( 1 +
vv A
β
) là nhỏ hơn 1.
Thông thường thì | Av | thì lớn hơn nhiều so với 1, đến mức chúng ta có thể xem gần đúng
v
vf
A
β
1
≅ (7.6)
7.2.2 Điện trở ngõ vào
Điện trở ngõ vào cho khuếch đại hồi tiếp được định nghĩa là tỉ số giữa Vs với I1.
Lấy Vf từ biểu thức (7.1) thế vào biểu thức (7.3), ta được
11
(1 )
s
vo v v
VV VV A
β
β
=+ = + (7.7)
Chúng ta có thể thay V1 = RiI1. Như thế
)1(
1
vvi
s
if AR
I
V
R
β
+== (7.8)
Khi điện áp hồi tiếp âm được sử dụng, điện trở ngõ vào được tăng lên.
7.2.3 Điện trở ngõ ra.
Giả sử rằng dòng được lấy ra từ mạng hồi tiếp như trong hình 7.2 thì rất nhỏ không đáng
kể, chúng ta có thế viết
Vo = AvV1 – IoRo (7.9)
Người soạn: NGUYỄN NGỌC MAI KHANH Bộ Môn Kỹ Thuật Điện Tử
Trang 7.4
Thế V1 từ biểu thức (7.3) chúng ta có
oofvsv RIVAVAV −−=
0 (7.10)
Sau đó sắp xếp lại ta được biểu thức:
oosvvvo RIVAAV −=+ )1(
β
(7.11)
Chia hai vế cho (1 )
vv
A
β
+ , chúng ta được
vv
o
osvfo A
R
IVAV
β
+
−= 1 (7.12)
Chúng ta tìm được điện trở ra của mạch hồi tiếp bằng cách cho Vs = 0
vv
o
o
o
of A
R
I
V
R
β
+
=
−
=1 (7.13)
Khi hồi tiếp âm, điện trở ra có hồi tiếp thì thấp hơn điện trở vào khi không có hồi tiếp.
7.2.4 Mạch tương đương
Biểu thức (7.12) đưa ra được một mạch tương đương cho ngõ ra của bộ khuếch đại hồi
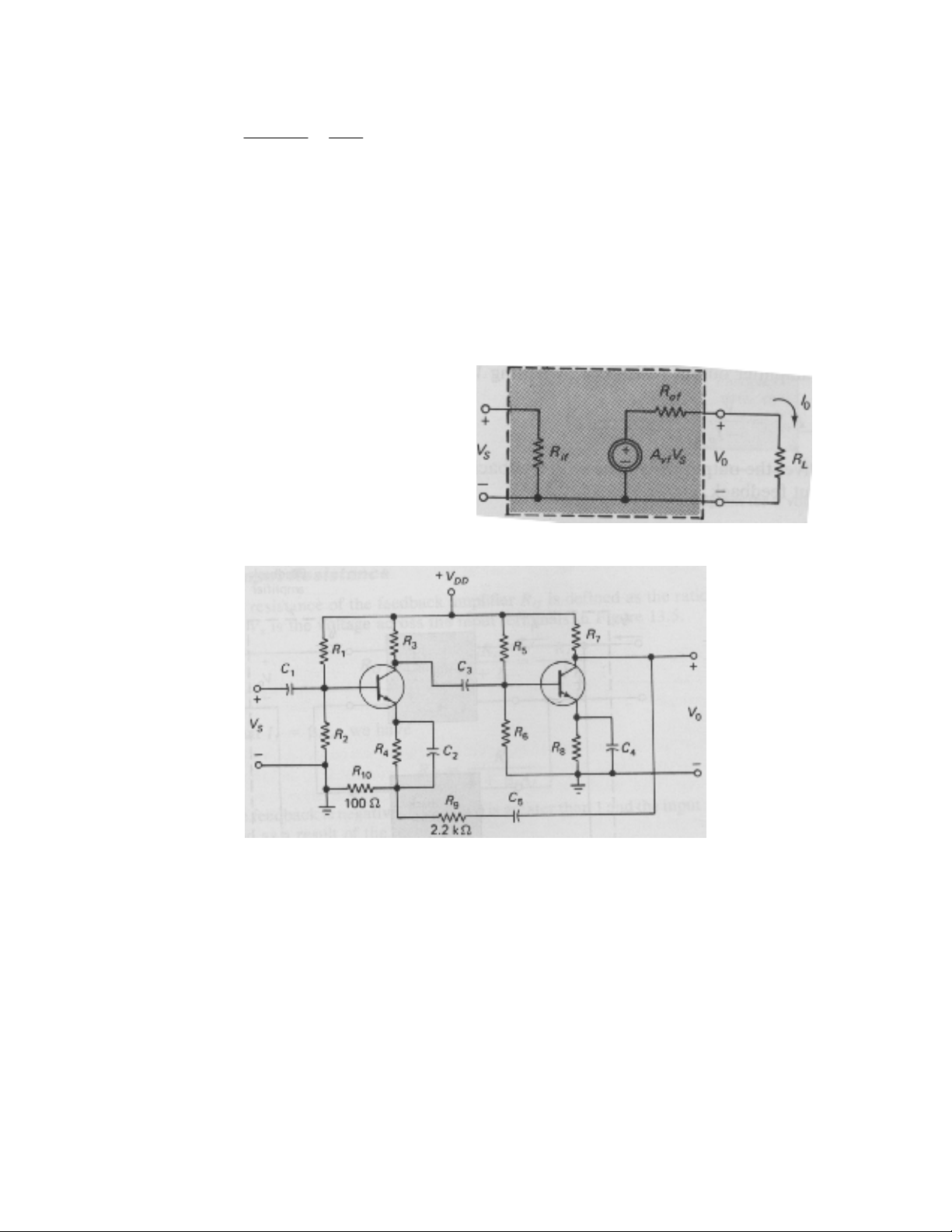
tiếp. Mạch tương đương hoàn chỉnh của mạch khuếch đại hồi tiếp được cho ở hình 7.3.
Các cách xác định các thông số của mạch khuếch đại hồi tiếp áp được minh họa ở ví dụ
7.1.
Ví dụ 7.1
Một mạch khuếch đại như ở hình 7.4 là một mạch khuếch đại hồi tiếp áp. Bao gồm mạng
hồi tiếp của điện trở phân áp R9 và R10. Khuếch đại không hồi tiếp có các thông số Av
=100, Ri = 2 k, và Ro = 5 k. Xác định các thông số của mạch khuếch đại khi hồi tiếp?
Giải
Hệ số hồi tiếp βv được tính từ tỉ số điện trở:
23
1
2.21.0
1.0
910
10 =
+
=
+
=RR
R
v
β
Kế tiếp chúng ta tìm thành phần hồi tiếp:
35.5
23
100
11 =+=+ vv A
β
Các thông số khuếch đại hồi tiếp áp có thể được tính toán như sau:
Ω
≅
Ω
×≅+= kkARR vviif 7.1035.52)1(
β
( theo 7.8)
Ω≅Ω≅Ω≅
+
=93935.0
35.5
5
1kk
A
R
R
vv
o
of
β
(theo 7.13)
Người soạn: NGUYỄN NGỌC MAI KHANH Bộ Môn Kỹ Thuật Điện Tử
Trang 7.5
7.18
35.5
100
1≅≅
+
=
vv
v
vf A
A
A
β
(theo 7.5)
Chú ý khi sử dụng gần đúng trong biểu thức (7.6) chúng ta có Avf ≈ 23, trong trường hợp
này là một số gần đúng nguyên. số gần đúng này được sử dụng khi vv
A
lớn hơn 10.
Tính toán độ lợi, trở kháng vào và trở kháng ra cho mạch khuếch đại không có hồi tiếp
phải được tính riêng, bởi vì phần hồi tiếp không thể được bỏ qua hoàn toàn. Tính toán
cho ngõ vào, bộ khuếch đại trong hình 7.4 không có hồi tiếp phải được xem như có Vo =
0 (ngắn mạch ngõ ra).
Hình 7.4 : Ví dụ về mạch khuếch đại hồi tiếp điện áp
Tính toán cho ngõ vào, bộ khuếch đại phải được xem như có Vf = 0 ( trong trường hợp
này, R10 bị ngắn). Tuy nhiên trở kháng ngõ vào trong ví dụ này được xem như không có
sự kết hợp của R1 và R2 mắc song song. Trở kháng tổng ngõ vào bao gồm hai điện trở đó.
7.3 KHUẾCH ĐẠI HỒI TIẾP DÒNG
Toàn bộ tín hiệu trong hình 7.1 là nguồn dòng, mạch là một bộ khuếch đại hồi tiếp dòng.
Sơ đồ khối được mô tả ở hình 7.5. Hồi tiếp âm được tạo ra làm cho dòng ngõ ra trừ với
dòng ngõ vào.
Hình 7.3 : Mạch tương đương
của khuếch đại hồi tiếp điện áp