Người soạn: NGUYỄN NGỌC MAI KHANH Bộ Môn Kỹ Thuật Điện Tử
Trang 6.1
Chương 6: Mạch khuếch đại đa tầng
6.1 Các quan hệ độ lợi trong mạch khuếch đại đa tầng
Trong nhiều ứng dụng, một mạch khuếch đại đơn không thể cho tất cả mọi độ lợi theo yêu cầu
của từng loại tải riêng biệt. Ví dụ, một hệ thống loa là một tải “nặng” trong hệ thống khuếch
đại âm thanh, nhiều tầng khuếch đại được đặt ra nhằm nâng mức tín hiệu gốc từ microphone
hoặc đầu đọc băng từ lên đến mức hiệu quả để có thể cho ra công suất đủ lớn tại loa. Ta đã biết
đến các mạch tiền khuếch đại, mạch khuếch đại công suất và mạch khuyếch đại ngõ ra, các
mạch khuyếch đại này đều là các mạch khuếch đại có cấu tạo nhiều tầng trong một hệ thống.
Thật ra bản thân mỗi bộ phận này có thể bao gồm nhiều tầng khuếch đại bán dẫn riêng. Các
mạch khuếch đại tạo ra độ lợi áp, dòng hay công suất thông qua việc sử dụng từ hai tầng trở lên
gọi là mạch khuếch đại đa tầng.
Khi ngõ ra của một tầng khuếch đại được nối với ngõ vào của một tầng khuếch đại khác thì gọi
là ghép Cascade
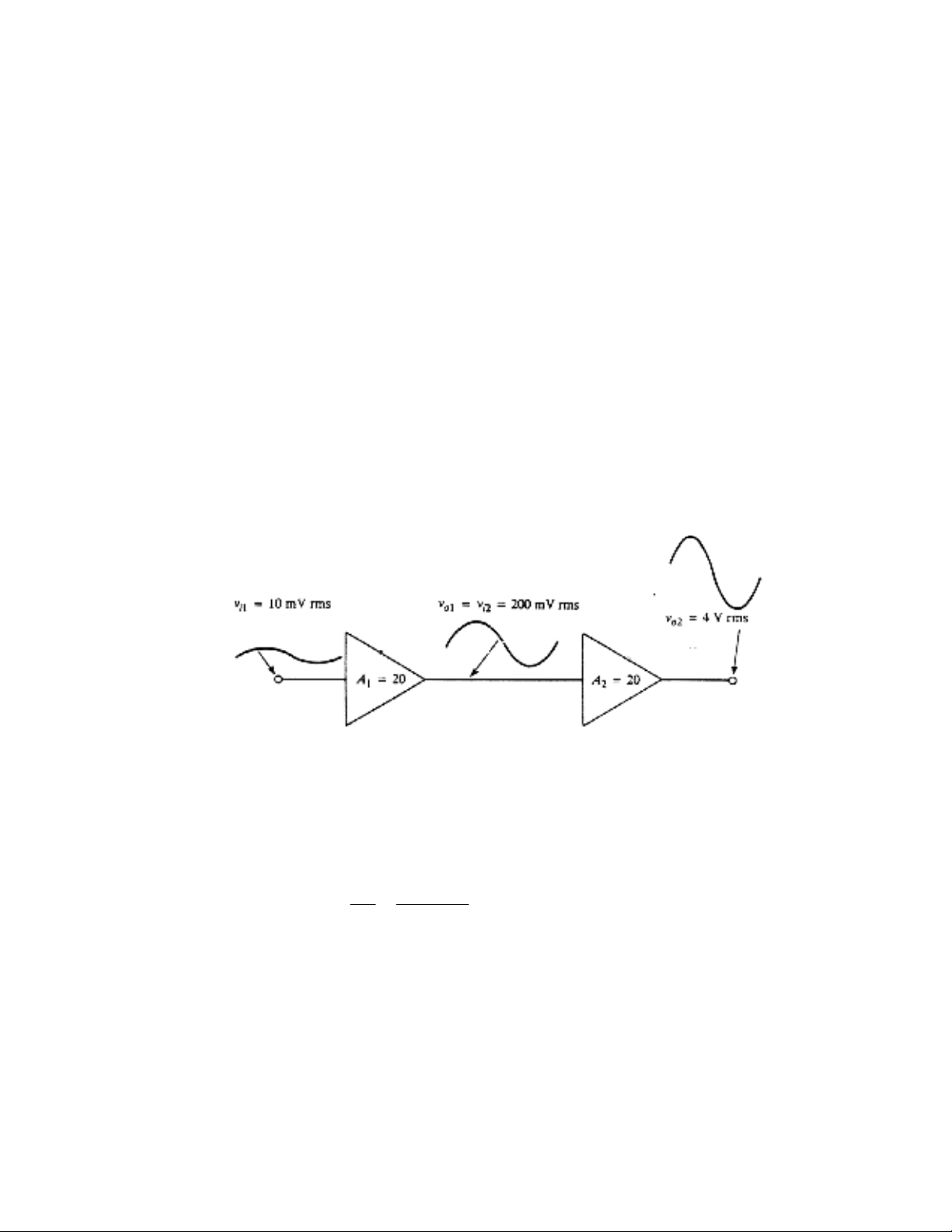
Hình 6.1: Hai tầng khuếch đại ghép cascade
Tổng độ lợi áp của hệ thống được tính như sau: Xem ngõ vào tầng 1 là 10 mV rms và độ lợi áp
của mỗi tầng là A1=A2=20, ngõ ra tầng 1 là A1vi1=20(10 mV rms)= 200 mV rms. Như vậy ngõ
vào tầng 2 là 200 mV rms. Tương tự ngõ ra tầng 2 là A2vi2=4 V rms. Độ lợi tổng sẽ là:
400
10
4
1
2=== mVrms
Vrms
v
v
A
i
o
v
chú ý là 400)20)(20(
21 === AAAv
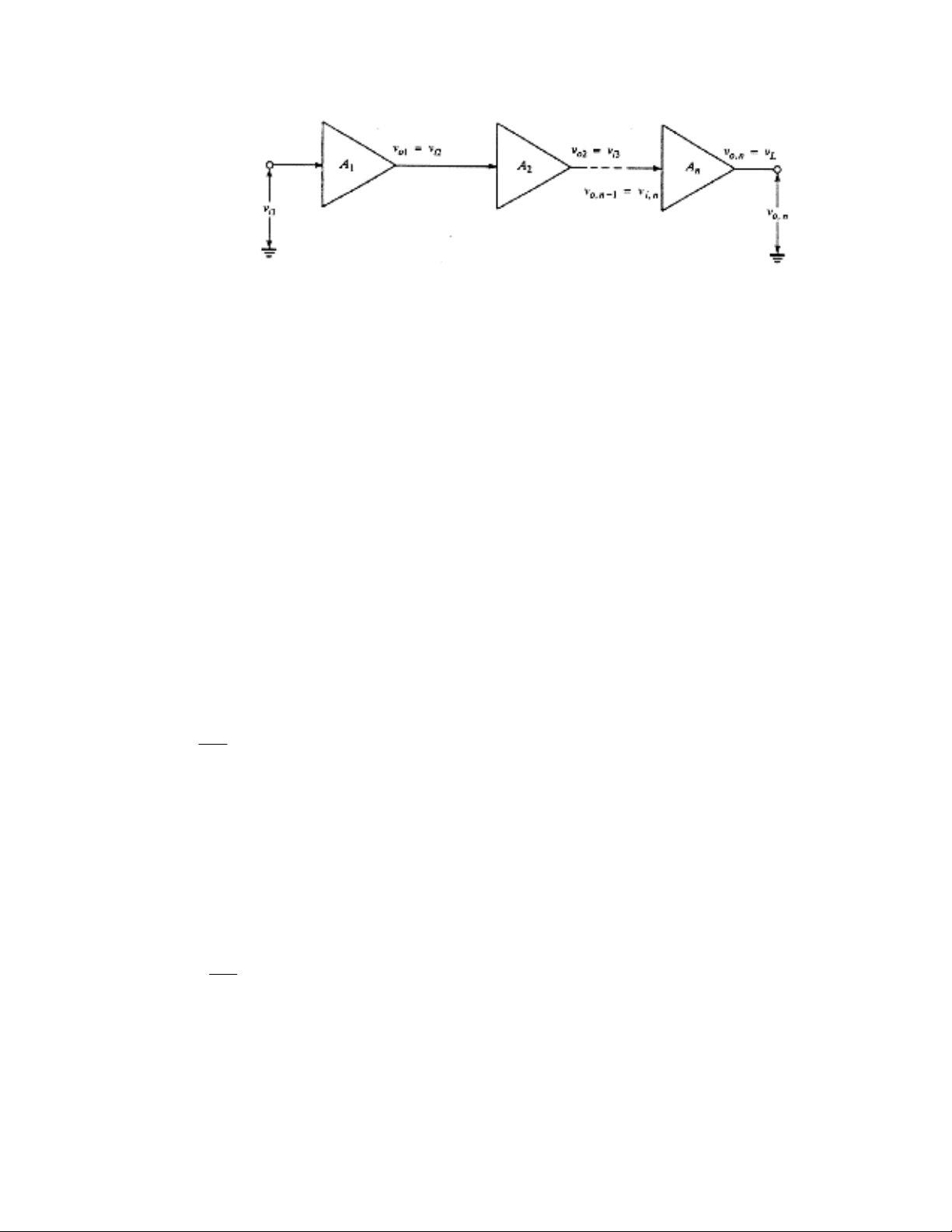
Hình 6-2 là một hệ thống gồm n tầng ghép Cascade. Ngõ ra của mỗi tầng chính là ngõ
vào của tầng kế tiếp ( vo1 = vi2, vo2 = vi3,…). Ta sẽ bắt đầu từ việc biểu diễn độ lợi áp tổng
vo,n/vi1 theo từng độ lợi tầng A1, A2 ,…, An. Xem độ lợi mỗi tầng như là giá trị độ lợi áp giữa
ngõ vào và ngõ ra của tầng đó khi các tầng được ghép với nhau.
Người soạn: NGUYỄN NGỌC MAI KHANH Bộ Môn Kỹ Thuật Điện Tử
Trang 6.2
Hình 6.2: n tầng khuếch đại được ghép cascade. Áp ngõ ra của mỗi tầng là ngõ vào
của tầng kế tiếp
Theo định nghĩa:
111 io vAv = (6-1)
12222 oio vAvAv
=
= (6-2)
thay vo1 từ (6-1) vào (6-2):
1212 )( io vAAv = (6-3)
Tương tự:
23333 oio vAvAv ==
từ (6-3):
13213 )( io vAAAv =
Theo cách này ta tìm được:
1121, ).............( innno vAAAAv −
=
Từ đó:
121
1
,............. AAAA
v
v
nn
i
no
−
= (6-4)
Phương trình 6-4 cho thấy tổng độ lợi áp của n tầng cascade là tích độ lợi từng tầng (không
phải tổng). Tổng quát, bất kỳ một hay nhiều tầng có độ lợi âm thì tầng đó gây ra một sự đảo
pha 180o. Theo phương trình 6-4, mạch khuếch đại cascade sẽ có ngõ ra ở tầng cuối cùng
không cùng pha với ngõ vào ở tầng thứ nhất nếu số tầng đảo pha là số lẻ, và cùng pha nếu là số
chẵn (hoặc bằng 0).
Để tìm độ lợi áp tổng của hệ thống ghép Cascade theo Decibel, ta bỏ qua dấu đại số của độ lợi
mỗi tầng và tính như sau:
)()(....................)()(
log20log20....................log20log20
).............(log20log20
121
11021011010
12110
1
,
10
dBAdBAdBAdBA
AAAA
AAAA
v
v
nn
nn
nn
i
no
++++=
++++=
=
−
−
−
(6-5)
Người soạn: NGUYỄN NGỌC MAI KHANH Bộ Môn Kỹ Thuật Điện Tử
Trang 6.3
Phương trình 6-5 cho thấy độ lợi áp tổng theo dB là tổng các độ lợi từng phần biểu diễn theo
dB. Tương tự ta có thể dễ dàng tìm được độ lợi dòng, độ lợi công suất tổng theo độ lợi các
tầng.
Kết quả của phương trình 6-4 không tính đến ảnh hưởng của điện trở nguồn và điện trở
tải lên độ lợi áp tổng. Điện trở nguồn rs tạo ra phân áp ở đầu vào của tầng thứ nhất, và điện trở
tải tạo ra phân áp giữa điện trở tải và tổng trở ra của tầng cuối cùng.
Trong trường hợp này, độ lợi áp tổng giữa tải và nguồn tín hiệu trở thành:
+
+
=−
Lno
L
nn
iS
i
S
L
rr
r
AAAA
rr
r
v
v
,
121
1
1............. (6-6)
Với ri1 là điện trở ngõ vào tầng đầu tiên và ro,n là điện trở ngõ ra tầng cuối.
Ví dụ 6-1:
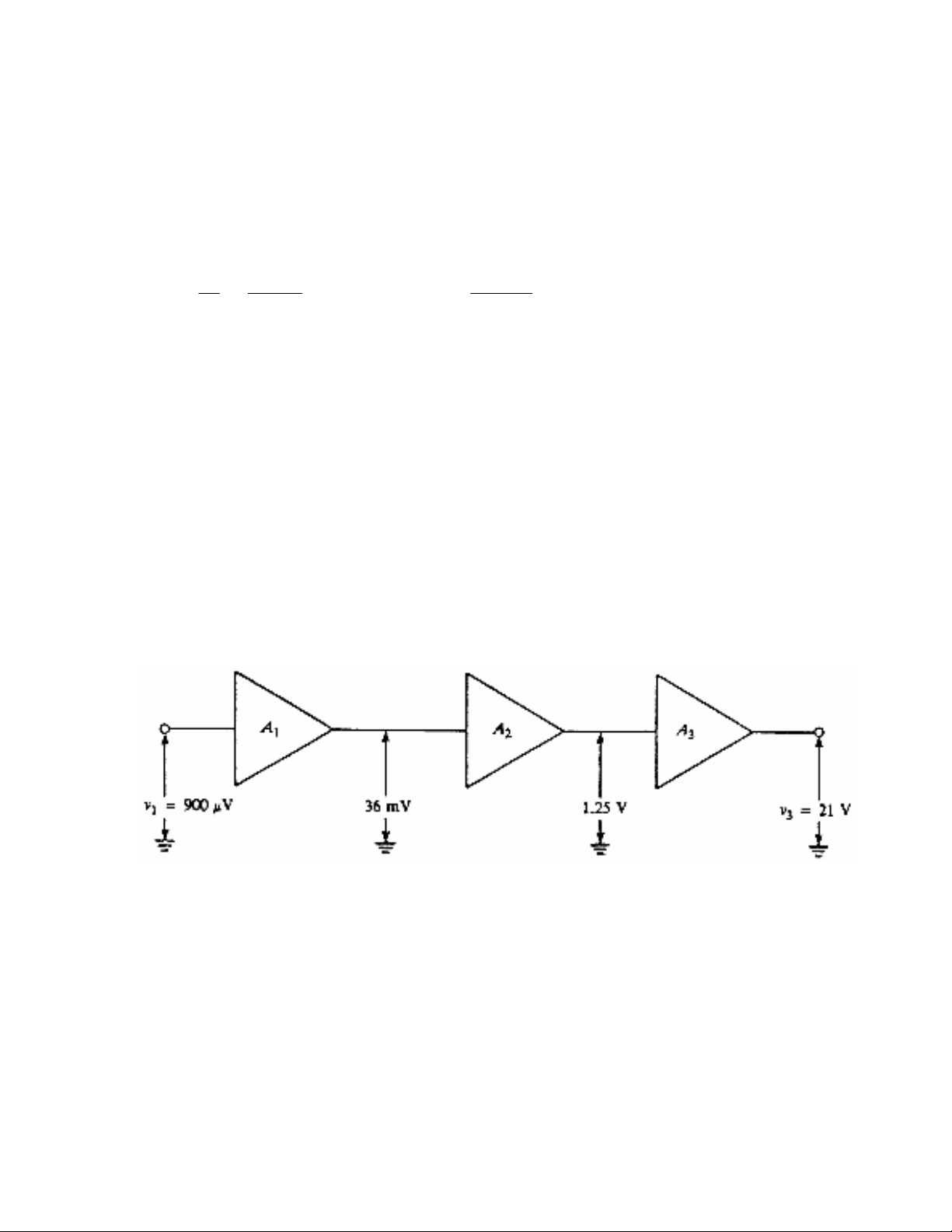
Hình 6-3 là một mạch khuếch đại 3 tầng và điện áp tại các điểm trong mạch khuếch đại là điện
áp hiệu dụng AC. Cho v1 là điện áp nguồn tín hiệu không trở ở đầu vào và v3 là điện áp ra
không tải
1. Tìm độ lợi áp mỗi tầng và độ lợi áp tổng v3/v1.
2. Làm lại câu 1 theo dB
3. Tìm độ lợi áp tổng vL/vs khi mạch khuếch đại đa tầng có điện trở nguồn là 2000Ω và
điện trở tải là 25Ω. Tầng 1 có điện trở vào là 1kΩ và tầng 3 có điện trở ra là 50Ω.
4. Làm lại câu 3 theo dB với độ lợi áp ở tầng thứ 2 được giảm xuống 6dB.
5. Tính độ lợi công suất theo dB với dữ liệu của câu 3.
6. Tính độ lợi dòng tổng iL/i1 ở câu 3.
Hình 6.3: (thí dụ 6 -1)
Giải:
1.
333.23)8.16)(722.34)(40(/
8.16)25.1/()21(
722.34)36/()25.1(
40)900/()36(
32113
3
2
1
===
==
==
=
=
AAAvv
VVA
mVVA
VmVA
µ
Người soạn: NGUYỄN NGỌC MAI KHANH Bộ Môn Kỹ Thuật Điện Tử
Trang 6.4
Chú ý rằng tích các độ lợi áp bằng độ lợi áp tổng. Trong ví dụ này, có thể tính độ lợi áp tổng
trực tiếp: 333.23)900/()21(/ 13
=
=VVvv
µ
.
2.
dBdBAdBAdBAdBvv
dBdBA
dBdBA
dBdBA
36.87)()()()(/
51.24)8.16(log20)(
81.30)722.34(log20)(
04.3240log20)(
32113
103
102
101
=++=
==
==
=
=
Để ý là dBxvv 36.87)333.23(log20)]10900/21[log20)/(log20 10
6
101310 === −
3. Từ phương trình 6-6:
5.2592
2550
25
)333.23(
10002000
1000 =
+
+
=
L
L
v
v4.
4. Độ lợi áp có nguồn và tải là dB27.68)5.2592(log20 10
=
. Do độ lợi tầng 2 giảm đi 6dB nên
độ lợi tổng là: dBdBdB 27.62)6()27.68(
=
−
5. Khi điện trở nguồn là 2000Ω được đưa vào ngõ vào thì v1 trở thành:
VVv
µµ
300)900(
10002000
1000
1=
+
=
Công suất ngõ vào là:
pW
x
r
v
P
i
i
i90
1000
)10300( 26
1
2
===
−
Khi đó điện áp qua tải 25Ω là:
VV
Rr
R
AAAvv
Lo
L
L
33.2
2550
25
)8.16)(722.34)(40)(300(
)(
3
3211
=
+
=
+
=
µ
Công suất ngõ ra có tải là
W
R
v
P
L
L
o217.0
25
)33.2( 2
2
===
Cuối cùng:
dB
x
P
P
dBA
i
o
v82.93
1090
217.0
log10log10)( 12
1010 =
=
=−
6. Nhắc lại ivp AAA =. Dùng kết quả câu 5, độ lợi công suất giữa ngõ vào và tầng thứ nhất, và
tải là:
Người soạn: NGUYỄN NGỌC MAI KHANH Bộ Môn Kỹ Thuật Điện Tử
Trang 6.5
9
12 1014.2
1090
217.0 x
x
P
P
A
i
o
p=== −
7. Độ lợi áp giữa ngõ vào và tầng thứ nhất, và tải là:
7766
300
33.2
1
=== V
V
v
v
AL
V
µ
Do đó:
5
9
101.3
7766
1014.2 x
x
A
A
A
v
p
i===
Điều quan trọng cần nhớ là phương trình độ lợi ta có được là dựa trên giá trị A1, A2… xác định
trong mạch, nghĩa là dựa trên các độ lợi tầng khi tất cả các tầng được ghép với nhau. Do đó suy
ra rằng mỗi giá trị độ lợi được tính vào tải của tầng trước đó và tải thì tính vào tầng kế tiếp.
Nếu biết độ lợi áp hở mạch và giá trị tổng trở vào và ra, ta có thể tính được độ lợi tổng bằng
cách tính tác động của tải của mỗi tầng lên các tầng khác. Về mặt lý thuyết, tải của một tầng
cho trước phụ thuộc vào tất cả các tầng nằm bên phải nó, tổng trở vào của một tầng bất kỳ phụ
thuộc vào tổng trở tải ngõ ra của nó cũng là tổng trở vào của tầng tiếp theo. Trong thực tế, ta có
thể bỏ qua tác động tải tích lũy của các tầng ngoại trừ một tầng ghép ngay với tầng đang xét,
hoặc giả sử rằng điện trở vào là tải của một tầng kế cận.
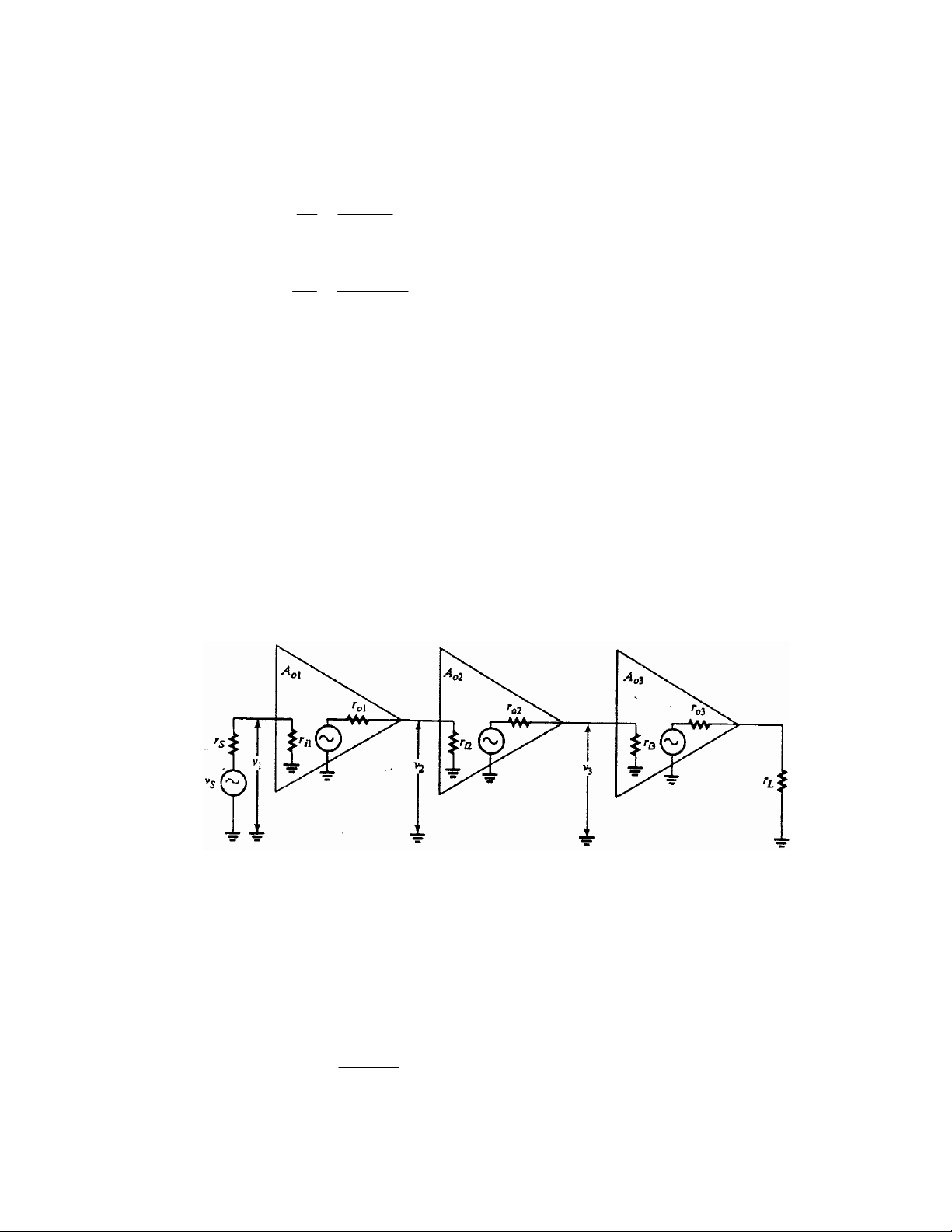
Hình 6-4 là một mạch khuếch đại 3 tầng, cho trước độ lợi áp hở mạch của các tầng là A01,A02,
và A03, điện trở vào và ra của mỗi tầng.
Hình 6.4: Một bộ khuếch đại 3 tầng. Ao1, Ao2, và Ao3 là 3 độ lợi áp hở mạch (không tải) của
các tầng
Phân áp tại các nút trong hệ thống ta có:
S
iS
iv
rr
r
v
+
=
1
1
1
Kết hợp lại ta có:
+
=
21,
2
112
io
i
orr
r
vAv (6-7)