
ME4181 2(2-1-0-4)
Chapter 1: Introduction
Chapter 2: Energy principle
Chapter 3: Elastic problems
Chapter 4: Bar and truss
Chapter 5: Beam and Frame
Chapter 6: Plane stress and strain
Chapter 7: Numerical integration
OUTLINE Learning outcome
Review some fundamental theory about matrix.
Some fundamental theory about FEM.
Direct stiffness matrix for some 1-D elements
Spring element
Bar element
Shaft element
Beam element.
Resistor element
Heat conduction element.
Fluid-flow element.

1. Fundamentals of finite element method (FEM)
For problems involving complicated geometries, loadings, and
material properties, it is generally not possible to obtain analytical
mathematical solutions need to rely on numerical methods.
The finite element method (FEM) is a numerical method for solving
problems of engineering and mathematical physics (structural analysis,
heat transfer, fluid flow, mass transport, and electromagnetic potential).
FEM yield approximate values of the unknowns at discrete numbers
of points in the continuum. Hence this process of modeling a body by
dividing it into an equivalent system of smaller bodies (finite
elements) interconnected at points common (nodes) and/or boundary
lines and/or surfaces is called discretization.
1. Fundamentals of finite element method (FEM)
In FEM, we formulate the equations for each finite element and
combine them to obtain the solution of the whole body.
The solution for structural problems typically refers to determining the
displacements at each node and the stresses within each element
making up the structure that is subjected to applied loads.
In nonstructural problems, the nodal unknowns may be temperatures
or fluid pressures due to thermal or fluid fluxes.
1.1. Brief history of FEM
The modern development of the FEM began in the 1940s in the field
of structural engineering with line (one-dimensional) elements (bars
and beams) for the solution of stresses in continuous solids
(Hrennikoff,1941; McHenry, 1943).
In 1943, interpolation (or shape) functions are proposed setting up
the solution of stresses in a variational form.
Flexibility or force method (1947) and the stiffness or displacement
method (1953) have been developed for use in analyzing statically
redundant aircraft structures. However, they were cumbersome to
solve by hand.
1. Fundamentals of finite element method (FEM)
In 1954 matrix structural analysis methods have been developed by
using energy principles.
The first treatment of two-dimensional elements was by Turner et al.
in 1956. They derived stiffness matrices for truss elements, beam
elements, and two-dimensional triangular and rectangular elements
in plane stress and outlined the procedure commonly known as the
direct stiffness method.
The phrase was introduced by Clough in 1960.
Extension of the finite element method to three-dimensional
problems with the development of a tetrahedral stiffness matrix was
done in 1960s.
1.1. Brief history of FEM
1. Fundamentals of finite element method (FEM)
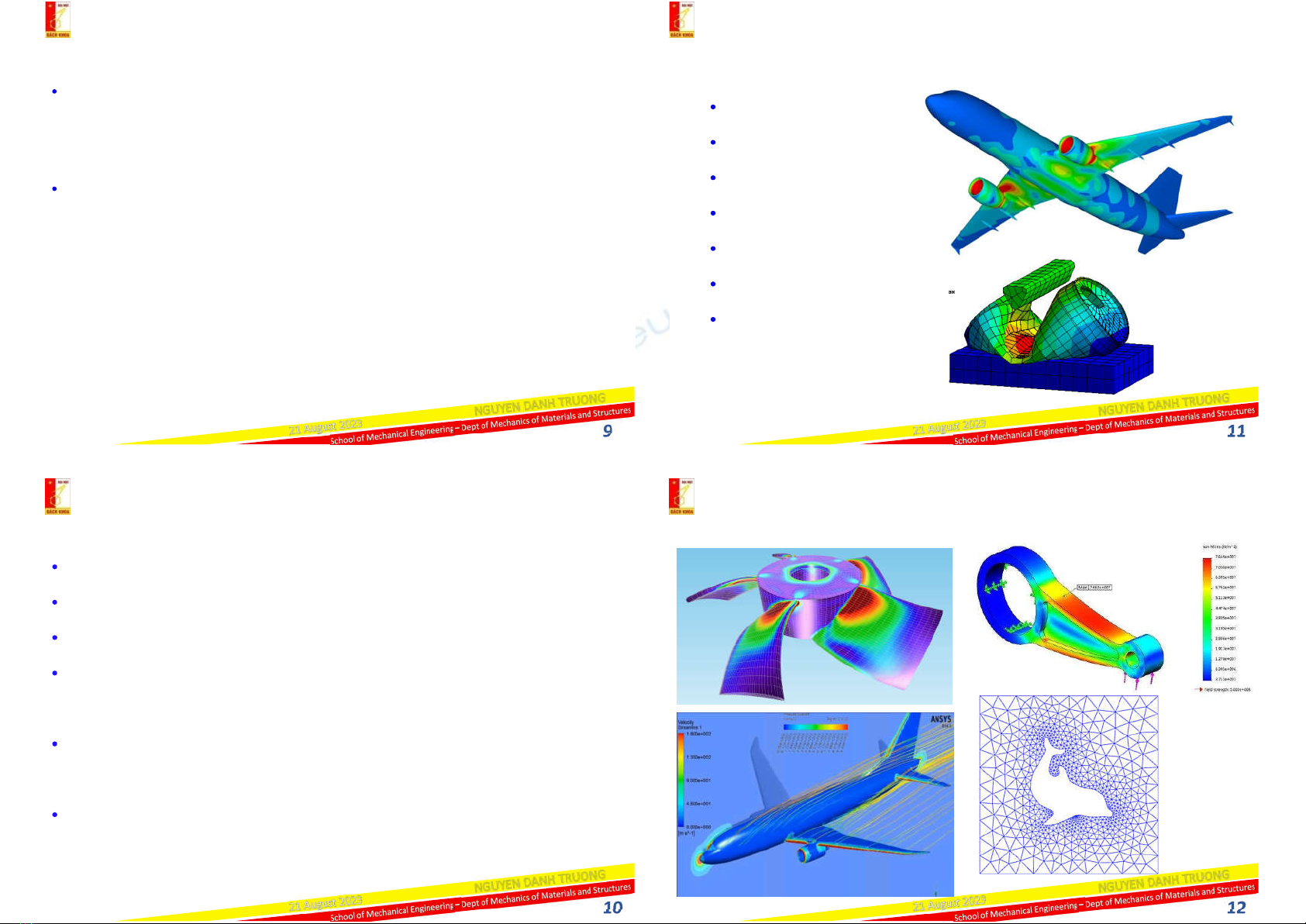
Most of the finite element work up to the early 1960s dealt with small
strains and small displacements, elastic material behavior, and static
loadings.
Until now, with the advent of the high-speed digital computer, FEM
are widely used to solve complicated engineering problems, applied
mathematicians, and other scientists such as: heat transfer, mass
transport, fluid flow, electrical networks, and so on.
1.1. Brief history of FEM
1. Fundamentals of finite element method (FEM)
1.2. Advantages of FEM
Model irregularly shaped bodies quite easily.
Handle general load conditions without difficulty.
Handle unlimited numbers and kinds of boundary conditions.
Handle nonlinear behavior existing with large deformations and
nonlinear materials.
Vary the size of the elements to make it possible to use small
elements where necessary.
Alter the finite element model relatively easily and cheaply.
1. Fundamentals of finite element method (FEM)
1.3. Some finite element programs
Abaqus
ANSYS
COSMOS/M
LS-DYNA
MARC
MSC/NASTRAN
SAP2000
1. Fundamentals of finite element method (FEM)
1.4. Some application of FEM
1. Fundamentals of finite element method (FEM)
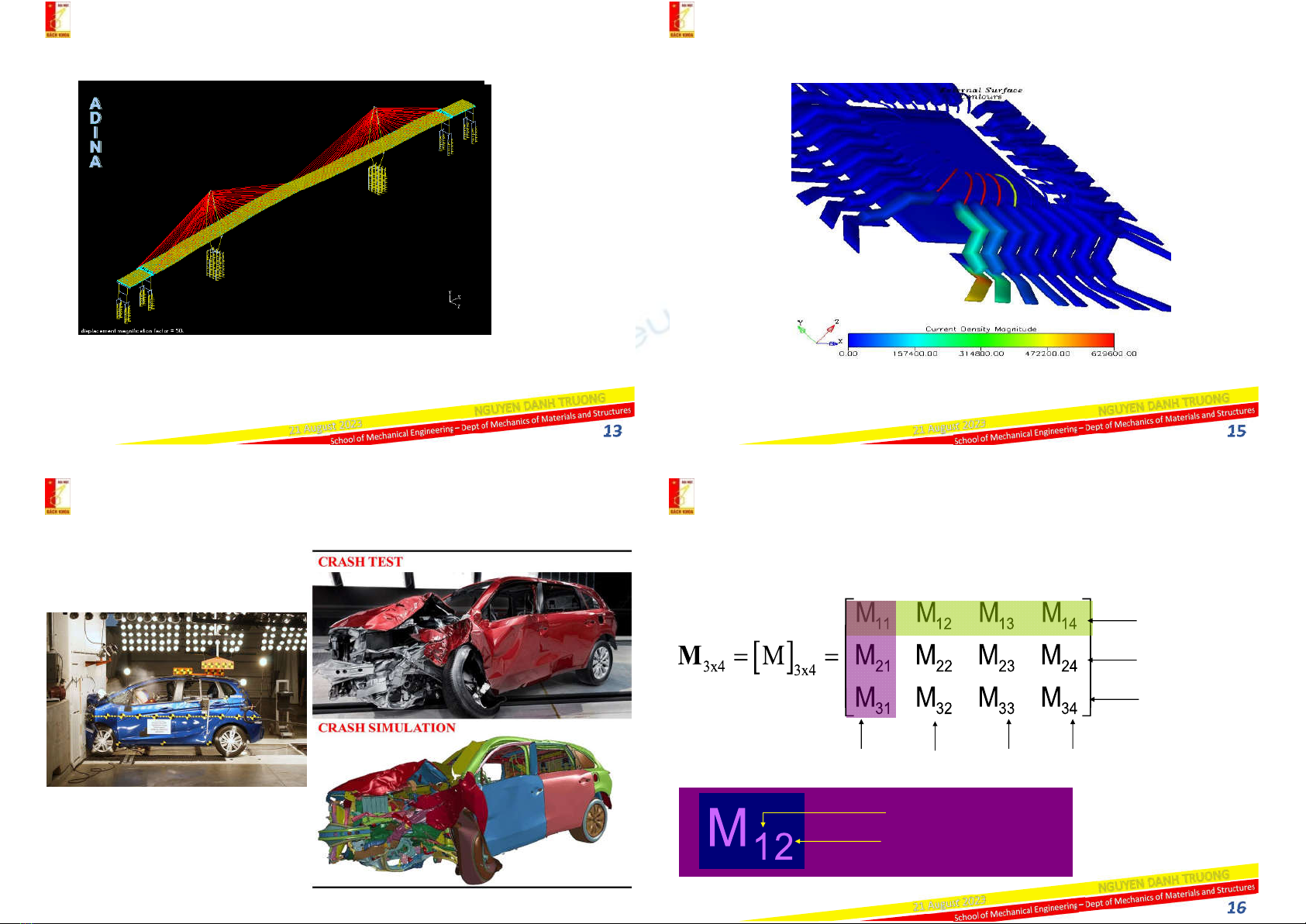
Using FEM for the seismic analysis of the famous San Francisco
Oakland Bay Bridge.
1. Fundamentals of finite element method (FEM)
1.4. Some application of FEM
1. Fundamentals of finite element method (FEM)
1.4. Some application of FEM
Using FEM in electromagnetic analysis of packages for electronic chips.
1. Fundamentals of finite element method (FEM)
1.4. Some application of FEM
A matrix is a rectangular array of quantities arranged in rows and
columns that is often used as an aid in expressing and solving a system
of algebraic equations
Column 1 2 3 4
Row 1
Row 2
Row 3
Row index
Column index
2. Review some fundamental theory about matrix
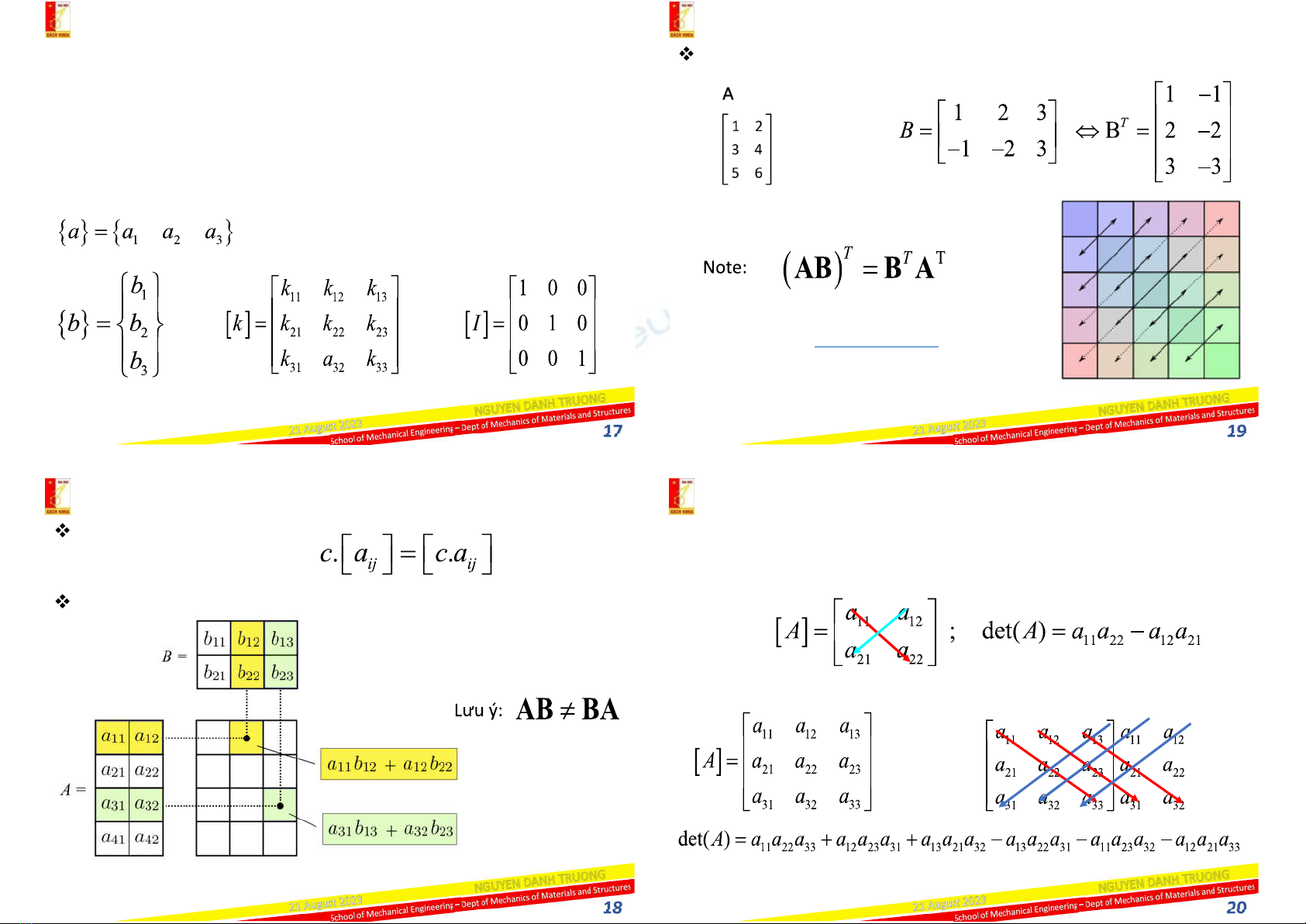
Matrices with size of 1 x n are called row vector.
Matrices with size of n x 1 are called column vector.
Matrices with size of n x n are called square matrix.
Square matrices with size of n x n in which all the elements on the
main diagonal are equal to 1 and all other elements are equal to 0
called identity matrix (or unit matrix).
2. Review some fundamental theory about matrix
Matrix multiplication
Scalar multiplication
2. Review some fundamental theory about matrix
Transposition
A square matrix Athat is equal to its transpose,
that is, A=AT, is a symmetric matrix.
2. Review some fundamental theory about matrix
The determinant is a scalar value that is a function of the entries
of a square matrix.
The determinant of a 2 × 2 matrix is:
The determinant of a 3 × 3 matrix is:
2. Review some fundamental theory about matrix











![Giáo trình Vật liệu cơ khí [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250909/oursky06/135x160/39741768921429.jpg)














