38
38
CHƯƠNG III:
PHÂN TÍCH ĐỘNG HỌC ROBOT SONG SONG 3RPS
3.1 Bài toán phân tích vị trí
3.1.1 Các phương trình liên kết cho Robot song song 3RPS tổng quát
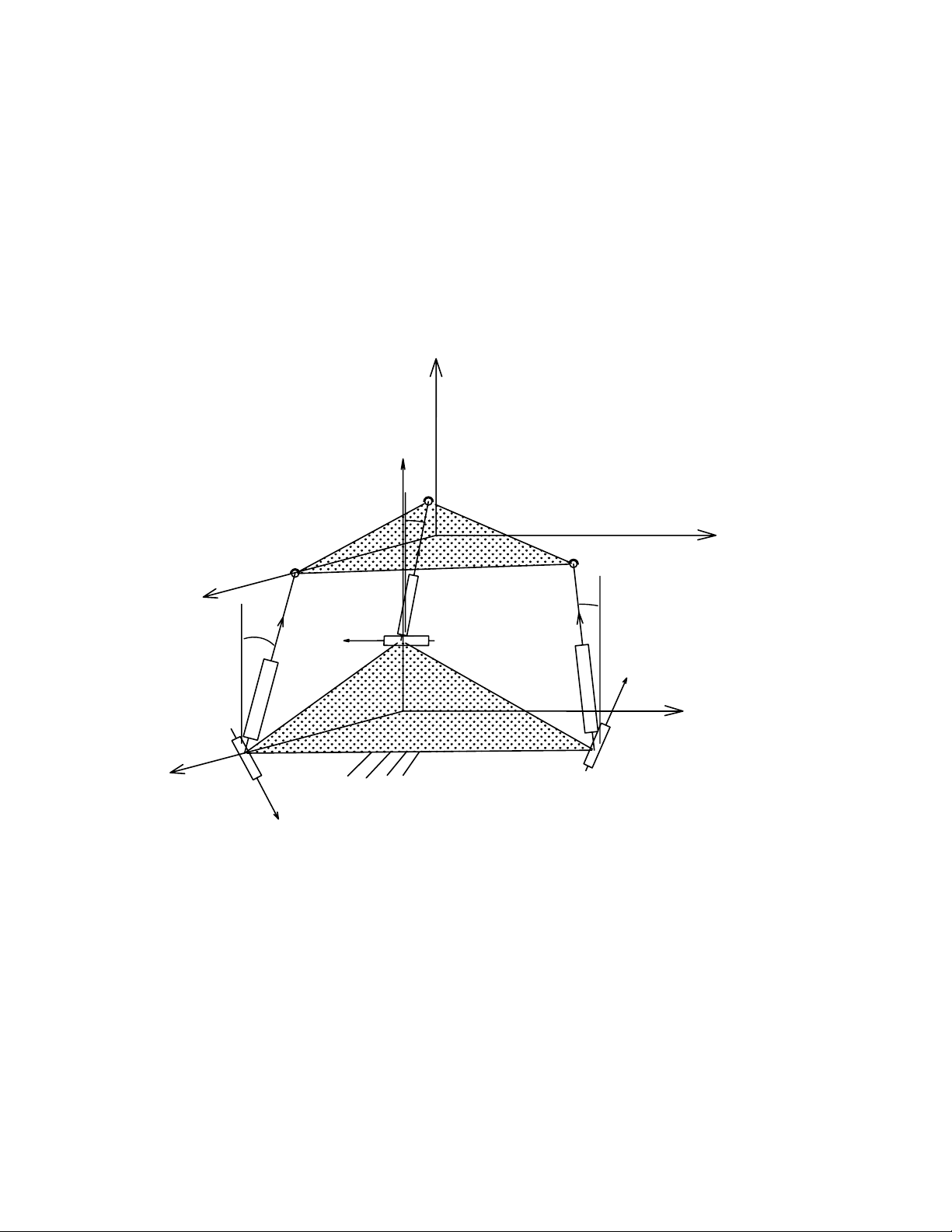
Trên hình 3.1 mô tả sơ đồ động học của Robot song song 3RPS. Cấu trúc các
khâu của Robot này được mô tả trong mục 1.6
a) Quan hệ về hình học và các hệ toạ độ
Do cấu trúc Robot đảm bảo tính hợp lý nên các chân AiBi ⊥ Z
i (các trục
quay). Gọi O và P là trọng tâm của hai tam giác A1A2A3 và B1B2B3, ta đặt lên
đó các hệ toạ độ như trên hình 3.1:
- Ox0y0z0 : Hệ toạ độ cố định.
- Pxyz : Hệ toạ độ động gắn liền với bàn máy động.
- Aixiyizi, (i = 1,2,3): Hệ động gắn với chân thứ i. Với xi≡ii BA và zi≡ trục
quay, trục yi lập với xi và zi một hệ quy chiếu thuận.
Ta đưa thêm vào 3 toạ độ suy rộng αi (i = 1,2,3) là góc hợp bởi trục z0 và trục
xi như hình vẽ.
A1 A2
A3
B1
B3
B2
Hình 3.1: Cấu trúc chấp hành song song 3RPS
Đế cốđịnh
Bàn máy động
x0
y0
z0
x1
x1
x2
x3
z1
z2
z3
1
α
2
α
3
α
P
O
y1
z1

39
39
Ngoài ra ta sử dụng các ký hiệu:
- ai : Véc tơ đại số chứa các toạ độ của điểm Ai trên hệ cố định, ai=
[]
T
iii aaa 321 ,,
bi: Véc tơ đại số chứa các toạ độ của điểm Bi trên hệ cố định.
- Bbi : Véc tơ đại số chứa các toạ độ của điểm Bi trên hệ cố động, Bbi=
[]
T
iziyix b,b,b .
- p: véc tơ đại số chứa các toạ độ của điểm P trên hệ cố định, p = [p1,p2,p3]T.
- di: độ dài chân thứ i (di = AiBi).
- bi và Bbi : Xác định được từ kết cấu hình học của robot.
- ARB : Ma trận cosin chỉ hướng của hệ động Pxyz so với hệ cố định Ox0y0z0.
- ARi : Ma trận cosin chỉ hướng của hệ động Aixiyizi so với hệ cố định
Ox0y0z0.
ARB
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
zzz
yyy
xxx
wvt
wvt
wvt
, ARi
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
iziziz
iyiyiy
ixixix
wvu
wvu
wvu
với: (i = 1,2,3). (3.1)
Các phần tử của ma trận ARB và ma trân ARi tuỳ theo kết cấu của bàn đế cố
định, là hàm của góc αi.
Từ hình vẽ ta có:
i
iOAOB =+ iiBA (i = 1,2,3) (3.2)
OPOBi=+ i
PB (i = 1,2,3) (3.3)
Ta có thể biểu diễn (3.2) và (3.3) dưới dạng sau:
bi = ai + ARi.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
0
0
di
(i = 1,2,3) (3.4)
bi = p + ARB.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
0
0
di
(i = 1,2,3) (3.5)
Kết hợp hai phương trình trên ta có :
p + ARB.Bbi = ai + ARi.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
0
0
di
(i=1,2,3) (3.6)
40
40
Hệ thức (3.6) gồm có 9 phương trình chứa các ẩn là toạ độ diểm P, độ dài các
chân di, các góc αi. Khi giải các bài toán động học thuận/ngược, ta đã biết 3
thông số p/di nên công việc còn lại chỉ chỉ giải bài toán 6 phương trình 6 ẩn,
các thông số còn lại như hướng của bài máy động, hướng của các chân ii BA
sẽ được xác định khi đã biết các thông số này.
Hệ thức này có ý nghĩa rất quan trọng, qua đó ta có thể giải quyết bài toán
động học một cách trọn vẹn cả bài toán thuận và bài toán ngược, điều mà các
phương pháp trước đây chưa giải quyết được hay mới chỉ đưa ra cách giải
quyết bài toán thuận
b) Tính toán các phần tử của hệ thức (3.6)
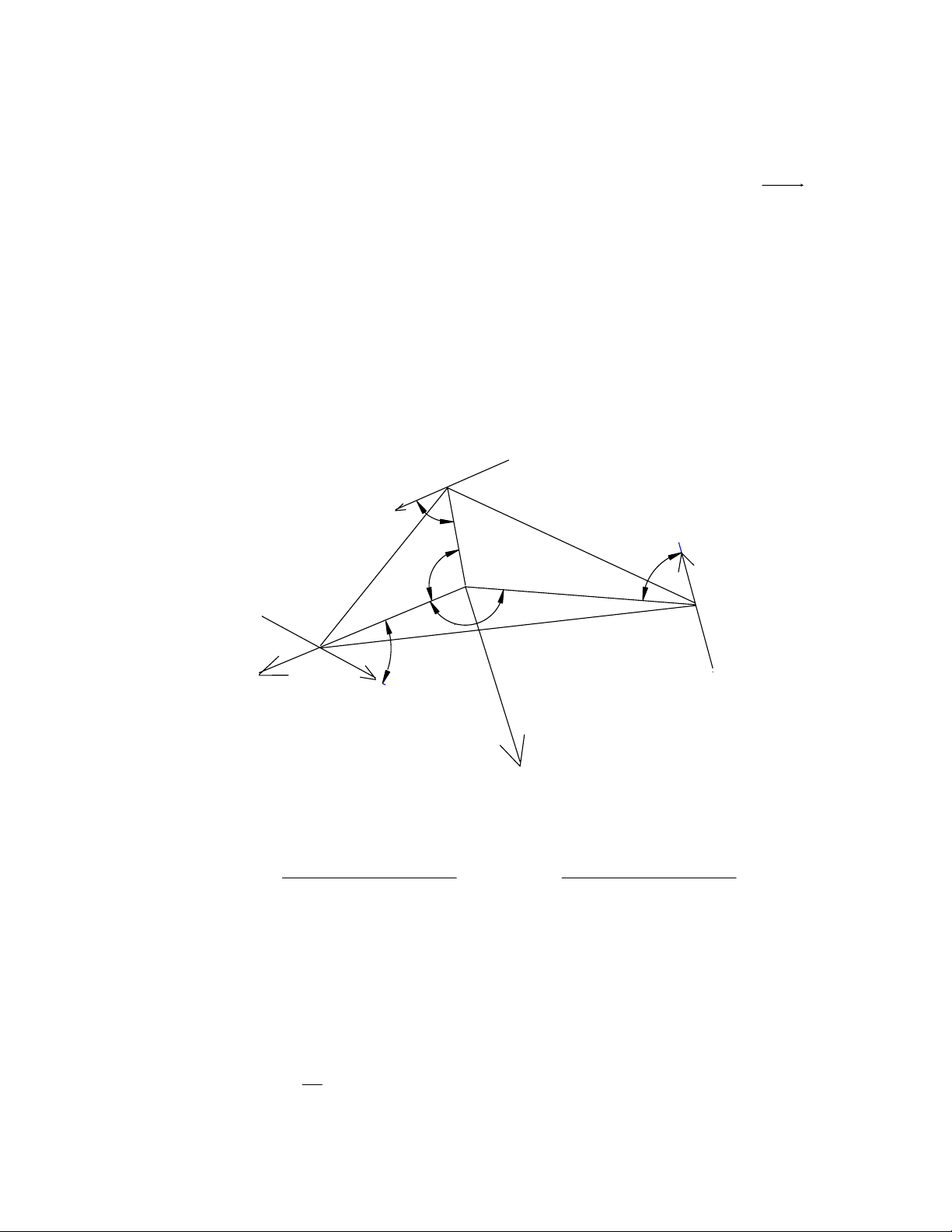
Các ma trận cosin chỉ hướng ARi được xác định bởi các phép quay liên tiếp
dựa vào lý thuyết trình bày ở mục 2.2, ta thực hiện các phép biến đổi liên tiếp
để hệ toạ độ cố định Oxyz trùng với hệ Aixiyizi .
Hình 3.2
Áp dụng hệ thức trong tam giác ta có thể tính được độ dài các đường trung
bình, như vậy sẽ xác định được ϕ2 và ϕ3.
cos ϕ2 =
21
2
21
2
2
2
1
OAOA2
AAOAOA ++ cos ϕ3 =
31
2
31
2
3
2
1
OAOA2
AAOAOA ++
Ma trận ARi được xác định bởi các phép quay liên tiếp từ hệ cố định quanh
chính nó như sau:
ARi = Az1. Ax2. Az3. Ax4
Với Az1 , Ax2 , Az3 , Ax4 lần lượt là ma trận cosin chỉ hướng của các phép
quay sau:
-Quay một góc ( 1
2
β
−
∏) quanh trục z0.
Y0
Z2
Z1
Z3
2
ϕ
3
β
3
ϕ
β
1
2
β
X
0

41
41
-Quay tiếp quanh trục x của hệ mới một góc (Π/2)
-Quay tiếp quanh trục z của hệ mới một góc (Π/2 + α1)
-Quay tiếp quanh trục x của hệ mới một góc Π
Vậy :
AR1=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
α−α
α
−
α
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
ββ
β−β
100
010
001
.
000
1sincos
0cossin
.
010
100
001
.
100
0sincos
0cossin
11
11
11
11
AR1=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
αα
βαβαβ−
β
−
α
β
αβ−
0sincos
sincoscossincos
coscossinsinsin
11
11111
11111
Bằng cách tương tự ta cũng xác định được các ma trận AR2 và AR3
Ma trận AR2 được xác định bởi các phép quay sau:
- Quay hệ cố định một góc ( 22
2ϕ+β−
∏
) quanh trục z0.
- Quay tiếp quanh trục x của hệ mới một góc (Π/2).
- Quay tiếp quanh trục z của hệ mới một góc (Π/2 + α2).
- Quay tiếp quanh trục x của hệ mới một góc Π.
AR2=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
α−α
α
−
α
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
ϕ−βϕ−β
ϕ−β
−
ϕ−β
100
010
001
.
000
1sincos
0cossin
.
010
100
001
.
100
0)sin()cos(
0)cos()sin(
22
22
2222
2222
AR2=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
αα
ϕ−βαϕ−βαϕ−β−
ϕ−β
−
α
ϕ
−
β
α
ϕ−β−
0sincos
)sin(cos)cos(sin)cos(
)cos(cos)sin(sin)sin(
22
22222222
22222222
Ma trận AR3 được xác định bởi các phép rơ quay sau:
- Quay hệ cố định một góc ( 33
2
ϕβ
−−
∏
) quanh trục z0.
- Quay tiếp quanh trục x của hệ mới một góc (Π/2).

42
42
- Quay tiếp quanh trục z của hệ mới một góc (Π/2 + α3).
- Quay tiếp quanh trục x của hệ mới một góc Π.
AR3=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
α−α
α
−
α
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
ϕ−βϕ−β
ϕ−β−ϕ−β
100
010
001
.
000
1sincos
0cossin
.
010
100
001
.
100
0)sin()cos(
0)cos()sin(
33
33
3333
3333
AR3=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
αα
ϕ−βαϕ−βαϕ−β−
ϕ−β
−
α
ϕ
−
β
α
ϕ−β−
0sincos
)sin(cos)cos(sin)cos(
)cos(cos)sin(sin)sin(
33
33333333
33333333
Ta thấy các thành phần của các ma trận ARi (i=1,2,3) chỉ chưa các ẩn là các
góc αi còn ϕ2 , ϕ3 và βi (i=1,2,3) đã biết do kết cấu của robot.
Mặt khác dựa vào kết cấu của bàn di động B ta có :
(b1 – b2)T(b1- b2) = 2
21BB
(3.7)
(b1 – b3)T(b1- b3) = 2
31BB (3.8)
(b2 – b3)T(b2- b3) = 2
32 BB (3.9)
Với bi = ai + ARi.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
0
0
di
(i = 1,2,3)
Như vậy các thành phần của hệ thức (3.6) được xác định thông qua 9 ẩn số
α1, α2, α3, d1, d2, d3, p1, p2, p3 .
Khi giải quyết bài toá động học thuận hay ngược, ta biết trước được 3 ẩn (d1,
d2, d3 hoặc p1, p2, p3 ). Công việc còn lại chỉ phải giải hệ 6 phương trình 6 ẩn
số.
3.1.2 Bài toán động học thuận
Bài toán động thuận là bài toán biết độ dài các chân di (i=1,2,3), ta phải tìm vị
trí của bàn máy động p và ma trận ARB.
Ta thay các giá trị di vào hệ (3.6), ta được hệ 6 phương trình với 6 ẩn số là:
α1, α2, α3,, p1, p2, p3 .
3.1.3 Bài toán động học ngược


























