Độ đo phi đặc trưng dựa trên lý thuyết bằng chứng: Một số nghiên cứu

Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5

MỘT SỐ ĐỘ ĐO PHI ĐẶC TRƯNG

DỰA TRÊN LÝ THUYẾT BẰNG CHỨNG

Nguyễn Văn Thẩm1, Nguyễn Quỳnh Diệp1, Nguyễn Đỗ Kiều Loan2

1Trường Đại học Thủy lợi, email: thamnv@tlu.edu.vn

2Học viện Tài chính

1. GIỚI THIỆU CHUNG

Lý thuyết bằng chứng (Evidence theory),

trong đó có lý thuyết Dempster-Shafer, là một

trong các công cụ hiệu quả được dùng để xử

lý thông tin không chính xác, thông tin chưa

hoàn chỉnh và kết hợp dữ liệu từ nhiều nguồn

khác nhau. Để xử lý được tính không chính

xác của thông tin thì cần đo được mức độ

không chính xác của thông tin. Độ đo phi đặc

trưng (Non-specificity measure) là một trong

các độ đo có thể được sử dụng để đánh giá độ

chính xác của thông tin và giúp đưa ra các

quyết định dựa trên bằng chứng tin cậy, thay

vì dựa trên trực giác.

Bài báo tổng hợp một số độ đo phi đặc

trưng trong lý thuyết bằng chứng. Từ đó, đề

xuất độ đo phi đặc trưng mới.

2. NỘI DUNG

2.1. Một số khái niệm

Đặt





1,EE,n

 là một khung phân biệt

gồm một tập hữu hạn không rỗng chứa n biến

cố loại trừ lẫn nhau. Đặt n

h=2 . Tập lũy thừa

(Power Set) của  là một tập gồm h phần tử





1121

, , , , ,..., ..EEE .EEE  nn

Định nghĩa 1. [1] Hàm





0,1

:m

được gọi là một hàm xác suất cơ bản (Basic

Probability Assignment-BPA) nếu thỏa mãn

các tính chất sau:

(i)



0m (ii)













m



Định nghĩa 2. [1] Cho m là hàm BPA

trên . Hàm tri thức và hàm tin cậy của m

được định nghĩa lần lượt là:

(i)









Bf m







(ii)

 

Pf m



 

Hàm tri thức







được gọi là cận dưới

của xác suất sẽ gán cho . Hàm tin

cậy







được gọi là cận trên sẽ gán cho .

2.2. Một số độ đo phi đặc trưng

Định nghĩa 3. [2] Cho





ppE là

phân phối xác suất trên , độ đo Shannon

Entropy của m được định nghĩa như sau:





() log

mE mEEm m









Định nghĩa 4. [3] Cho m là hàm BPA

trên , độ đo nhập nhằng (Ambiguity

measure) của m được định nghĩa như sau:













() log

mm pE pE









trong đó: m

là xác suất pignistic.









NÕu 



Ng−îl¹i

















 













Định nghĩa 5. [2] Cho m là hàm BPA

trên , độ đo đặc trưng (Specificity

measure) của m được định nghĩa như sau:



() m

Sm m

 







Định nghĩa 6. [2] Cho m là hàm BPA

trên , độ đo phi đặc 1

Ns của m được định

nghĩa như sau:







lo(g)Nmsm











Định nghĩa 7. [2] Cho m là hàm BPA

trên , độ đo phi đặc trưng 2

Ns của m được

định nghĩa như sau:

Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5



() log

Ns m E







 









trong đó,







max Bf E E , *

thoả mãn



Bf E và

 





min ,EPfE



.

2.3. Đề xuất độ đo phi đặc trưng

Dựa trên độ đo Ns2, bài báo đề xuất độ đo

phi đặc trưng Ns3.

Thuật toán tính Ns3 được định nghĩa như

(1) Đầu vào: Một tri thức.

(2) Đầu ra: Độ đo phi đặc trưng.

(3) Phạm vi bài toán: Tri thức được biểu

diễn bằng BPA.

(4) Tiến trình tính độ đo:

Bước 1: Tính hàm tri thức Bf và hàm tin

cậy

f theo Định nghĩa 2.

Bước 2: Tìm hàm tin cậy đạt giá trị nhỏ

nhất:







min ii

Pf E E . Đặt *



sao

cho



Bf E .

Bước 3: Với mọi *

E, tính:

 





max ,Mi E Bf E E 

Bước 4: Tính độ đo phi đặc trưng:



() log

Ns m Mi E





 









2.4. Ví dụ tính toán và thảo luận

Sau khi xem xét nguồn nước của một khu

dân cư, phòng tài nguyên một huyện đưa ra

các nguyên nhân có thể gây ô nhiễm nguồn

nước là: nước thải nông nghiệp (N), hoạt

động y tế (H) và rò rỉ đường ống (R); và đưa

ra hai nhận định được cho trong Bảng 1.

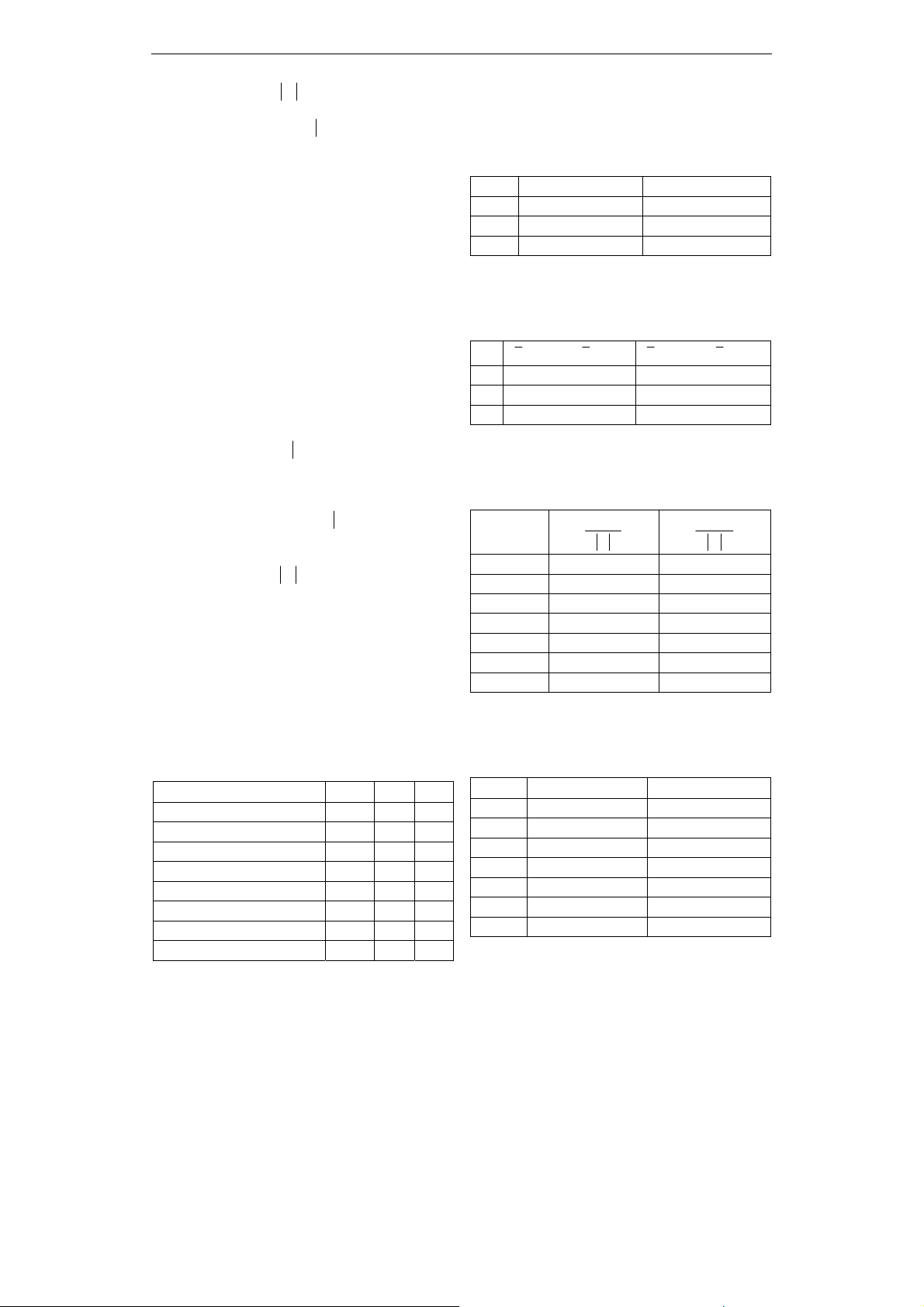
Bảng 1. Các hàm BPA

Sự kiện  m1 m2

N gây ra N 0.06 0.36

H gây ra H 0.25 0.45

R gây ra R 0.35 0.02

N hoặc H gây ra NH 0.13 0.1

N hoặc R gây ra NR 0.12 0.01

H hoặc R gây ra HR 0.08 0.05

Một trong 3 yếu tố gây ra NHR 0.01 0.01

Không yếu tố nào gây ra  0 0

Do đó,





,,NRH

và









,,,,,,,



 NHRNHNRHRNHR

2.4.1. Tính độ đo Em

Bảng 2. Kết quả tính Shannon Entropy

E m1(E)log2m1(E) m2(E)log2m2(E)

N -0.24 -0.53

H -0.50 -0.52

R -0.53 -0.11

Do đó, Em(m1) = 1.27 và Em(m2) = 1.16.

2.4.2. Tính độ đo Am

Bảng 3. Kết quả tính độ đo nhập nhằng

E 2

(E) ( ( ))

plogpE 2

(E) ( ( ))

plogpE

N -0.38 -0.24

H -0.35 -0.29

R -0.34 -0.16

Do đó, Am(m1) = 1.07 và Am(m2) = 0.69.

2.4.3. Tính độ đo Sm

Bảng 4. Kết quả tính độ đo đặc trưng

 1()m



2()m



N 0.06 0.36

H 0.25 0.45

R 0.35 0.02

NH 0.07 0.05

NR 0.06 0.01

HR 0.04 0.03

NHR 0.00 0.00

Do đó, Sm(m1) = 0.83 và Sm(m2) = 0.91.

2.4.4. Tính độ đo Ns1(m)

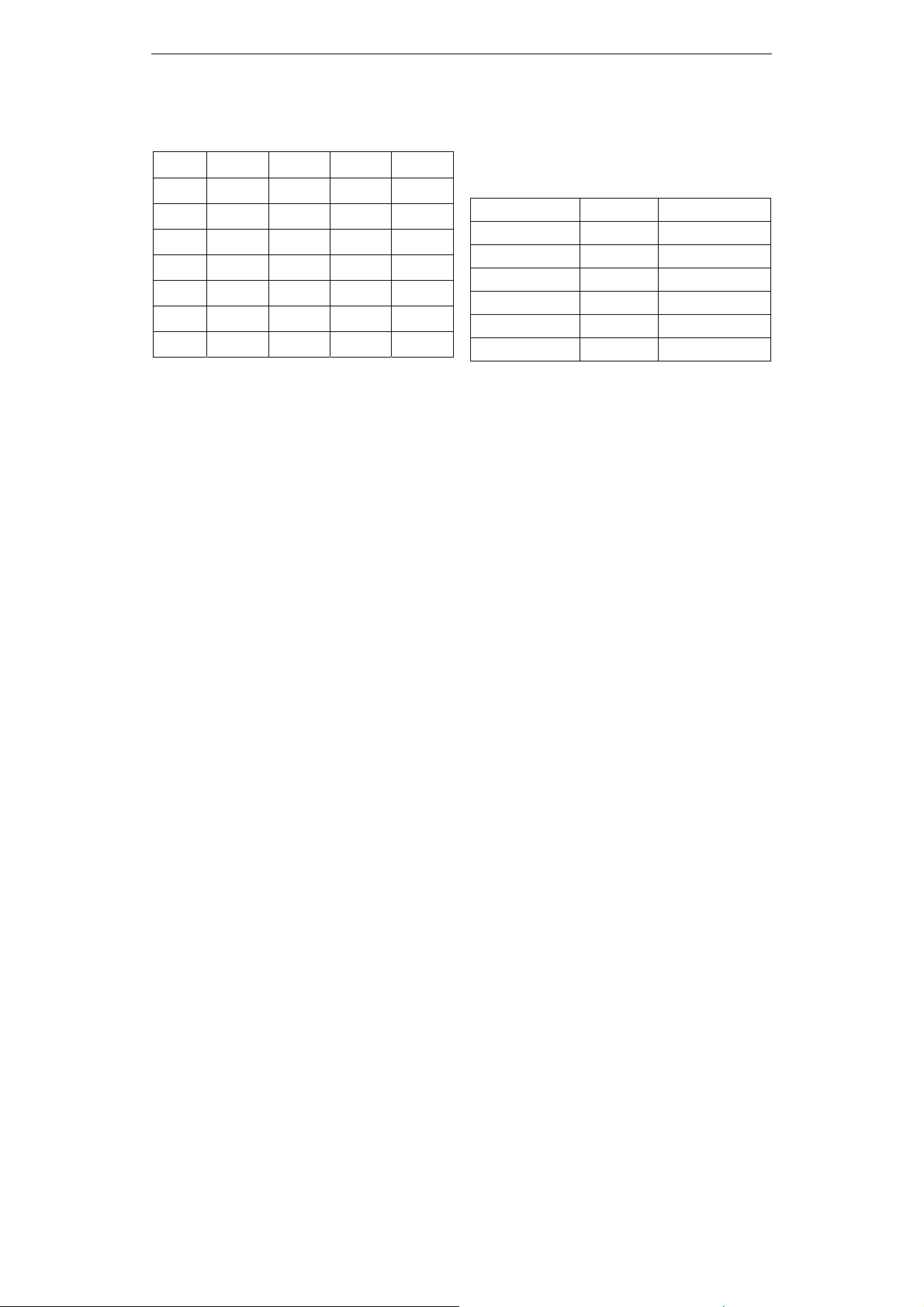
Bảng 5. Kết quả tính Ns1(m)

 m1()log2|| m2()log2||

N 0.00 0.00

H 0.00 0.00

R 0.00 0.00

NH 0.13 0.10

NR 0.12 0.01

HR 0.08 0.05

NHR 0.02 0.02

Do đó, Ns1(m1) = 0.35 và Ns1(m2) = 0.18.

Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5

2.4.5. Tính độ đo Ns2(m)

Bước 1: Tính các hàm Bf và Pf.

Bảng 6. Kết quả tính Bf1, Pf1 và Bf2, Pf2

 Bf1 Pf1 Bf2 Pf2

N 0.06 0.32 0.36 0.48

H 0.25 0.47 0.45 0.61

R 0.35 0.56 0.02 0.09

NH 0.44 0.65 0.91 0.98

NR 0.53 0.75 0.39 0.55

HR 0.68 0.94 0.52 0.64

NHR 0.01 1 0.01 1

Bước 2: Tính 10.35

b, *

R

và 20.45

b, *

H

Bước 3: Với 1



0.35Mi H ,





0.32Mi N 

Với 2



0.45Mi N ,



0.09Mi R 

Bước 4: 21

( ) 1.57Ns m 22

( ) 1.4Ns m .

2.4.6. Tính độ đo Ns3(m)

Bước 1: Tính các hàm Bf và Pf giống như

Bảng 5.

Bước 2: Tính 10.32 , *

N

và 20.09 , *

R

Bước 3: Với 1



0.32Mi H ,





0.35Mi R 

Với 2



0.36Mi N ,



0.45Mi H 

Bước 4: 31

( ) 1.59Ns m 32

( ) 1.86Ns m 

Từ Bảng 1, ta thấy rằng m1 tập trung vào R

(tức nhận định rò rỉ đường ống gây ô nhiễm

nguồn nước nhiều nhất), m2 tập trung vào H

(tức nhận định hoạt động y tế gây ô nhiễm

nguồn nước nhiều nhất). Đặt  hiệu của mức

độ tri thức lớn nhất và mức độ tri thức lớn

nhất lớn thứ 2. Từ Bảng 1, ta có 10.1

 và

20.09

 . Do đó, 12

, tức độ đo phi

đặc trưng của m1 nhỏ hơn của m2. So sánh

Ns3(m1) và Ns3(m2) thấy rằng, Ns3(m1) < Ns3(m2),

tức độ đo phi đặc trưng của m1 nhỏ hơn m2.

Như vậy, đo phi đặc trưng được đề xuất phù

hợp với phân tích trực quan.

Bảng 7 tổng hợp các độ đo phi đặc trưng

cho tri thức được cho trong Bảng 1.

Bảng 7. Tổng hợp các độ đo phi đặc trưng

Độ đo m1 m2

Em 1.27 1.16

Am 1.07 0.69

Sm 0.83 0.91

Ns1(m) 0.35 0.18

Ns2(m) 1.57 1.40

Ns3(m) 1.59 1.86

3. KẾT LUẬN

Trong bài báo này, một độ đo phi đặc

trưng Ns3 dựa trên lý thuyết bằng chứng

Demspter-Shafer đã được đề xuất. Độ đo Ns3

được xây dựng dựa trên độ đo Ns2. Ý tưởng

độ đo Ns3 là tìm phần tử E* đạt giá trị nhỏ

nhất  của hàm Pf, sau đó tìm giá trị lớn nhất

giữa hàm Bf của E  E* và , cuối cùng tính

độ đo phi đặc trưng; trong khi độ đo Ns2

được tính theo hướng ngược lại. Bài báo

cũng đã trình bày thuật toán để tính độ đo phi

đặc trưng. Tuy nhiên, bài báo mới xem xét về

mặt lý thuyết. Do đó, trong thời gian tới, các

kết quả lý thuyết này sẽ được kiểm thử trên

bộ dữ liệu thực tế.

4. TÀI LIỆU THAM KHẢO

[1] Gan, D., Yang, .B, Tang, .T. 2020. An

Extended Base Belief Function in Dempster-

Shafer Evidence Theory and Its Application

in Conflict Data Fusion. Mathematics.

[2] Song, Y., Wang, X., Wu, W. et al. 2018.

Evidence combination based on credibility

and non-specificity. Pattern Anal Applic 21.

167-180.

[3] Jousselme A-L, Liu C, Grenier D, Bosse E.

2006. Measuring ambiguity in the evidence

theory. IEEE Trans Syst Man Cybern A

Syst Hum 36(5). 890-903.

Một số độ đo phi đặc trưng dựa trên lý thuyết bằng chứng

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi