Journal of Science and Arts Year 14, No. 3(28), pp. 199-210, 2014
ISSN: 1844 – 9581 Mathematics Section
ORIGINAL PAPER
SOME NEW IDENTITIES ON THE CONIC SECTIONS
DAM VAN NHI1, TRAN TRUNG TINH1, PHAM MINH PHUONG2
_________________________________________________
Manuscript received: 15.08.2014; Accepted paper: 22.09.2014;
Published online: 30.09.2014.
Abstract. In mathematics, a conic section (or just conic) is a curve obtained as the
intersection of a cone (more precisely, a right circular conical surface) with a plane. In this
paper, we construct some new identities and proposed the concept of the power of a point
with respect to a conic.
Keywords: Conic section, identity, power line, power of a point.
2010 Mathematics Subject Classification: 26D05, 26D15, 51M16.
1. THE ECCENTRICITY OF CONIC SECTION
Definition 1.1. A conic section (or conic) is a curve in which, a plane, not passing
through the cone's vertex, intersects a cone.
Conics possess a number of properties, one of them consisting in the following result.
Proposition 1.2. [2] Each conic section, except for a circle, is a plane locus of points
the ratio of whose distances from a fixed point
F
and a fixed line
d
is constant. The point
F
is called the focus of conic, the line
d
its directrix.
Proof: Let
()
be the curve in which the plane
()P
intersects a cone. We inscribe a
sphere in the cone, which touches the plane
()P
at the point
F
. Let
()
ω
be the plane
containing the circle along which the sphere touches the cone. We take an arbitrary point
()∈M
and draw through it a generator of the cone, and denote by
B
the point of its
intersection with the plane
We then drop a perpendicular from
M
to the line
d
of
intrsection of the planes
()P
and
( ),
ω
example:
.⊥MA d
We obtain
=FM BM
because
they are the tangents to the sphere drawn from one point. Further, if we denote by
h
the
distance of
M
from the plane
then ,
sin
=
h
AM
α
,
sin
=
h
BM
β
where
α
is the angle
between the planes
()
ω
and
()P
and
β
is the angle between the generator of the cone and
the
Hence it follows that sin .
sin
= =
AM AM
FM BM
β
α
Thus, the ratio
sin
sin
= =
AM
FM
β
λα
does not depend on the point
M
.
฀
1 Hanoi National University of Education, Cau Giay, Hanoi, Vietnam. E-mail: tinhtckh@gmail.com.
2 Hanoi National University of Education, High School for Gifted Students, Hanoi, Vietnam.
Some new identities on the conic sections Dam Van Nhi et all
www.josa.ro Mathematics Section
200
We note that if
1<
λ
then
()
is an ellipse; if
1=
λ
then
()
is a parabola and if
1>
λ
then
()
is a hypebol. The number
λ
is called the eccentricity of the conic section.
Let us now pass over to rectangular Cartesian coordinates
in the plane
( ),P
where
(0,0)F
and
:.=dx p
Suppose that
( , ).Mxy
Then
=AM FM
λ
if and only if
2 2 2 2 22
(1 ) 2 0.− − +− =x pxy p
λλ λ
(1) If
1=
λ
and by putting
2−
px
by
x
then we obtain the canonical equation of the
parabola 2
( ): 2=P y px and
,0 , : .
22
()
= −
pp
F dx
(2) If
1<
λ
then
2 22
2 22
22
(1 ) .
11
()
− + +=
−−
pp
xy
λλ
λλλ
By putting for brevity
2
2
1
+−
p
x
λ
λ
by
x
and
22
2
22
,
(1 )
=−
p
a
λ
λ
22
2
2
1
=−
p
b
λ
λ
we get the canonical equation for the ellipse
22
22
( ): 1+=
xy
Eab
and
22
2 22
,0 , : .
1 11
()
=+=
− −−
p pp
F dx p
λλ
λ λλ
(3) If
1>
λ
then
2 22
2 22
22
(1 ) .
11
()
− + +=
−−
pp
xy
λλ
λλλ
By putting for brevity
2
2
1
+−
p
x
λ
λ
by
x
and
22
2
22
,
(1 )
=−
p
a
λ
λ
22
2
2
1
−=
−
p
b
λ
λ
we get the canonical equation for the hypebol
22
22
( ): 1
−=
xy
H
ab
and
2
22
,0 , : .
11
()=
−−
pp
F dx
λ
λλ
฀
2. PARAMETRIZATION AND POWER
Proposition 2.1. The parabol
2
( ) : 4 , 0,= ≠P y px p
is parameterized by
2
.
2.
=
=
x pt
y pt
Let the stright line
: ()= −+d x ky v u
be passed through by the point
(,)Nuv
which
intersected
()P
at the points
A
and
B
. With the point
(1, )Mk
belong to the stright line
1=x
we obtain the identity 2
2
.
4.
= −
NA NB v pu
OM
The ratio 2
.NA NB
OM
is called the {\rm power}
of the point
N
with respect to parabol
Proof: The coordinates of
,AB
are the solutions of consider
2
()
4.
= −+
=
x ky v u
px y
Consider the system of equations:
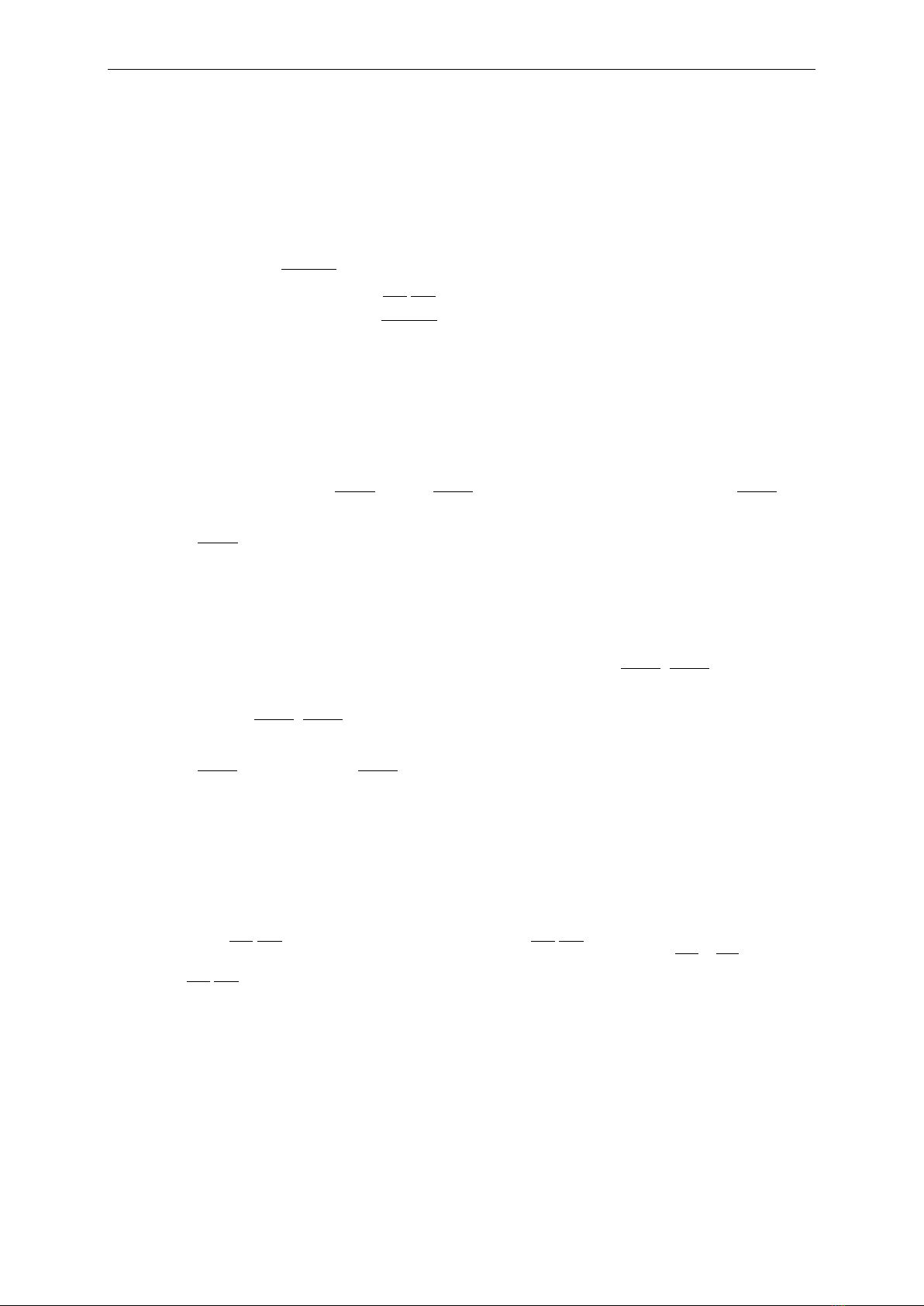
Some new identities on the conic sections Dam Van Nhi et all
ISSN: 1844 – 9581 Mathematics Section
201
2
()
4 4 4 0.
−= −
− + −=
x u ky v
y pky pkv pu
Let
12
,yy
are the solutions of equation
2
4 4 4 0.− + −=y pky pkv pu
Inaddition, we
have
11 1
( ( ) , ),= −+Ax k y v uy
22 2
( ( ) , ).= −+Bx ky v uy
Thus, we have
2
12
2
.| ( )( ) | | 4 |.= − −=−
NA NB y v y v v pu
OM
Hence, we have identities 2
2
.
4.
= −
NA NB v pu
OM
Because of
( ,0)Ip
, the power of a
focus point
I
with respect to the Parabol
()P
is
2
4.−p
฀
Exercise 2.2. Constructing power lines of two parabols.
Proposition 2.3. The circle
22
( ): 1+=Cx y
is a rational planar graphs in
฀
,
parameterized by
2
22
21
() , ()
11
−
= =
++
tt
xt yt
tt
, provided that
2
2
( ) lim 0,
1
t
t
xt
→∞
∞= =
+
2
2
1
( ) lim 1
1
t
t
y
t
→∞
−
∞= =−
+. The equation of the tangent line
At
to
()C
at a point 00
( , ) ()
∈
Ax y C
is
00
1.+=xx yy
Proof: Equation of a line
()d
through point
(0;1) ( )∈C
with slope
−t
is
( ) : 1.=−+d y tx
The line
()d
meet
()C
at the points
(0;1)
and
2
22
21
,.
11
()
−
++
t
tt
Att
The point
2
22
21
,
11
()
−
++
tt
tt
could be anywhere in
()C
except
(0; 1).−
Provided that
2
22
21
( ) lim 0, ( ) lim 1,
11
→∞ →∞
−
∞= = ∞= =−
++
tt
tt
xy
tt
t
A
could be
(0; 1).−
Due to 00
( , ) ()∈Ax y C
, we have
22
00
1.+=xy
Thus,
000 0
:2 ( ) 2 ( ) 0−+ −=
At x x x y y y
, in other words,
00
: 1.
+=At xx yy
฀
Proposition 2.4. Given
22 2
( ): .+=Cx y R
Provided that
(,)Nuv
and a line with slope
tan=k
α
through point
N
, meet
()C
at
A
and
.B
Consider the point
( sin , cos )MR R
αα
in
()C
, we have
22 2
.=+−NA NB u v R
, in other words,
22
24
22
. . 1.
()
= +−
uv
NA NB OM R
RR
We
say that
2
..NA NB OM
is the power of a point
N
with respect to circle
review
Proposition 2.6.
Proof: We could easily obtain this result.
฀
Some new identities on the conic sections Dam Van Nhi et all
www.josa.ro Mathematics Section
202
Proposition 2.5. The ellip
22
22
( ): 1
+=
xy
E
ab
is parameterized by
2 3 22
2 22 2 22
2
() , () −
= =
++
a bt b a bt
xt yt
b at b at
with convention
2
2 22
3 22
2 22
2
( ) lim 0
( ) lim .
→∞
→∞
∞= =
+
−
∞= =−
+
t
t
a bt
xb at
b a bt
yb
b at
Proof: The line
()d
through
(0; ) ( )∈bE
with slope
−t
:
( ): .=−+d y tx b
()d
meets
()E
at
(0; )b
and
2 3 22
2 22 2 22
2
,.()
−
++
t
a bt b a bt
A
b at b at
The point
2 3 22
2 22 2 22
2,
()
−
++
t
a bt b a bt
A
b at b at
through all points of
( ),E
exept
(0; ).−b
With convention that
2 3 22
2 22 2 22
2
( ) lim 0, ( ) lim
→∞ →∞
−
∞= = ∞= =−
++
tt
a bt b a bt
xyb
b at b at
deduce
t
A
through
(0; ).−b
\par\noindent Since 00
( , ) ()∈
Ax y E
we have
22
00
22
1.+=
xy
ab
Hence
00
00
22
22
: ( ) ( )0−+ −=
xy
At x x y y
ab
or
00
22
: 1.+=
xx yy
At ab
฀
Proposition 2.6. The ellip
22
22
( ): 1+=
xy
Eab
with
,ab∈
and the focus points
( ,0),Fc
( ,0).
′−Fc
Construct a line through the focus point
F
, meet ellip
()E
at
A
and
B
. We have
(1)
2
1 12
.+=
a
FA FB b
(2) Minimum value of
AB
is
2
2.
b
a
(3) Assuming
(,)Nuv
and a line through
N
with slope
tan=k
α
meet
()E
at
C
and
D
. With the point
( sin , cos ) ( )∈Ma b E
αα
we have
22
2 22
22
. . 1.()= +−
uv
NC ND OM a b ab
We call
2
..NC ND OM
is the power of the point
N
respect to ellip
(4) The power of the focus point
F
respect to ellip
()E
2
..FA FB OM
is
4
.−b
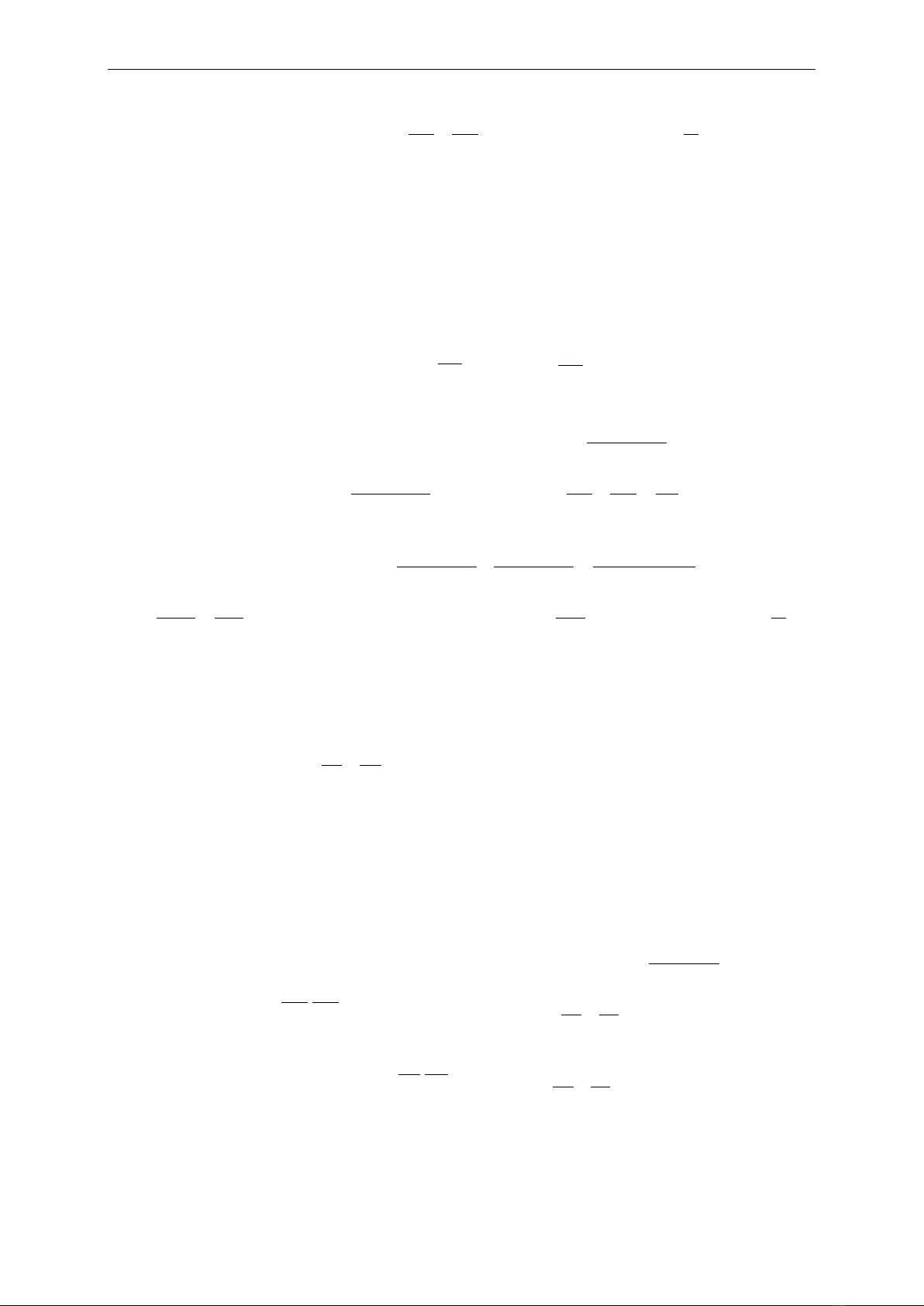
Some new identities on the conic sections Dam Van Nhi et all
ISSN: 1844 – 9581 Mathematics Section
203
Proof: (1) We calculate
11
.= +TFA FB
Assuming ,
2
=∠≤
xFA
π
α
=r FA
and
11
( , ).Ax y
Draw
.⊥AP Ox
We have
cos=FP r
α
and x-axis of
A
:
1cos .= +x cr
α
Thus, we
have
2 2 22 22
11111
2
( ) ( ) 4.
′
+=
′
− = − +− + −=−
FA F A a
FAFAxcyxcy cx
We deduce
1
2
2
′
+=
′
−=−
r FA a
cx
r FA a
and
1
.= − cx
ra a
We have
22
1( cos )=−=−+aracxaccr
α
or
2
.
cos
= = +
b
FA r ac
α
Similary, we have
2
.
cos
=−
b
FB
ac
α
We deduce
2
1 12
.=+=
a
TFA FB b
(2) From
22 2
222
2
cos cos cos
=+= + =
+− −
b b ab
AB FA FB
ac ac a c
αα α
we deduce
22
2
22
.≥=
ab b
AB aa
Thus, the minimum value of
AB
is
, equality holds if
2
=
π
α
or
.⊥FA Ox
(3) The Equation
: ()= −+NC y k x u v
or
= +y kx h
with
.= −h v ku
Coodinates of
C
and
D
are solutions of
22
22
1.
= +
+=
y kx h
xy
ab
Let
12
,
xx
are two solutions of equation
2 22 2 2 22 22
( ) 2 0.+ + +−=b ak x hkax ah ab
Thus, we have
11 1
(, ( ) )= −+Cx y kx u v
and 22 2
(, ( ) )= −+Dx y kx u v.
Deduce
2
12
. | ( )( ) | (1 ).=−− +NC ND u x u x k
From
2 22 2 2 22 22 2 22
12
( ) 2 ( )( )( )+ + +−=+ − −b ak x hkax ah ab b ak x x x x
we have
222 222222
12
( )( )( ) .+ − −= + −b ak u x u x bu av ab
Deduce
2
2 22 22 22
12 2 22
1
. |( )( )|(1 ) | | +
=− − += + − +
k
NC ND u x u x k b u a v a b
b ak
.
Conclude that
22
2 2 2 2 22
22
. ( cos sin ) 1 .
()
+ = +−
uv
NC ND b a a b
ab
αα
(4) From
2 22
= −
cab
, deduce
22
2 22 4
22
0
.. 1 .()= + −=−
c
FA FB OM a b b
ab
฀
Exercise 2.7. Constructing power line of two ellipse.