KHOA HỌC - CÔNG NGHỆ
58
SỐ 80 (11-2024)
TẠP CHÍ ISSN: 1859-316X
KHOA HỌC CÔNG NGHỆ HÀNG HẢI
JOURNAL OF MARINE SCIENCE AND TECHNOLOGY
NGHIÊN CỨU HIỆU QUẢ CỦA PHƯƠNG PHÁP BỀ MẶT ĐÁP ỨNG
TRONG PHÂN TÍCH ỨNG XỬ KẾT CẤU
THE EFFECTIVENESS OF RESPONSE SURFACE METHOD IN STRUCTURAL
BEHAVIOR ANALYSIS
ĐOÀN NHƯ SƠN1*, TRẦN ANH TUẤN2
1Khoa Công trình, Trường Đại học Hàng hải Việt Nam
2Khoa Công trình, Trường Đại học Công nghệ Giao thông vận tải
*Email liên hệ: vanson.ctt@vimaru.edu.vn
Tóm tắt
Vì là chu trình ẩn, phương pháp phần tử hữu hạn
(FEM) thường yêu cầu thời gian tính toán lâu, gây
khó khăn cho các bài toán có yêu cầu tính lặp như
tính toán kết cấu theo lý thuyết độ tin cậy hay tối
ưu hóa. Nghiên cứu này ứng dụng phương pháp
bề mặt đáp ứng (response surface method) xây
dựng hàm thay thế ở dạng tường minh giúp cho
việc tính toán kết cấu được nhanh chóng và thuận
tiện hơn. Nội dung của RSM sẽ được trình bày
trong nghiên cứu này. Sau đó, tính hiệu quả và
chính xác của phương pháp sẽ được đánh giá
thông qua ba bài toán kết cấu. Kết quả thu được
từ các ví dụ cho thấy RSM có thể áp dụng tốt trong
bài toán phân tích ứng xử kết cấu. Hầu hết các mô
hình đều cho kết quả tương đương với kết quả từ
bài toán gốc, hiệu suất thấp nhất quan sát được
đối với chuyển vị tại đỉnh của khung phẳng (R² =
0,9897 sử dụng đa thức bậc hai đầy đủ). Kết quả
nghiên cứu tạo tiền đề cho các nghiên cứu sâu hơn
cần đến các tính toán lặp nhiều lần như bài toán
phân tích độ tin cậy hay thiết kế tối ưu.
Từ khóa: FEM, mô hình thay thế, phương pháp
bề mặt đáp ứng.
Abstract
The finite element method (FEM) is a widely used
tool for structural analysis. However, as an
implicit method, FEM often demands substantial
computational resources, posing challenges for
iterative applications like reliability-based
structural analysis and optimization. This study
explores the use of the response surface method
(RSM) to develop an explicit surrogate model,
facilitating faster and more efficient structural
computations. The principles of RSM are
introduced, followed by an assessment of its
effectiveness and accuracy through three
structural case studies. Results from these
examples demonstrate that RSM is well-suited for
analyzing structural behavior, with the lowest
performance observed for the displacement at the
top of a plane frame (R² = 0.9897 using a full
quadratic polynomial). These findings establish a
foundation for further research in iterative
computations, such as reliability analysis and
optimization design.
Keywords: Finite element method, surrogate
model, response surface method.
1. Mở đầu
Trong tính toán các bài toán kết cấu, phương pháp
phần tử hữu hạn (FEM) thường được sử dụng do có
thể kết hợp với máy tính. Trong quá trình tính toán, hệ
kết cấu được rời rạc hóa thành một số lượng hữu hạn
các phần tử. Phương trình cân bằng sẽ được thiết lập
cho từng phần tử, sau đó lắp ghép thành hệ phương
trình thể hiện mối quan hệ giữa lực và chuyển vị cho
toàn hệ kết cấu. Căn cứ vào hệ phương trình cân bằng,
chuyển vị sẽ được xác định cho toàn bộ nút. Sau đó,
các thành phần nội lực trong phần tử sẽ được xác định
thông qua chuyển vị tại nút của các phần tử.
Rõ ràng chu trình tính toán theo FEM là chu trình
ẩn vì chuyển vị và nội lực không được xác định dưới
dạng tường minh. Do đó, các tính toán thường yêu cầu
thời gian tính toán lâu khi số lượng phần tử lớn. Với
các tính toán có yêu cầu tính toán lặp lại nhiều lần khi
các tham số đầu vào thay đổi, các tính toán trực tiếp
phụ thuộc vào FEM khiến cho việc mô hình mất nhiều
thời gian hơn. Nhược điểm này khiến cho việc áp
dụng trực tiếp FEM trong các bài toán tối ưu hay bài
toán đánh giá xác suất mất an toàn bị hạn chế. Ví dụ,
các bài toán tối ưu hóa thường yêu cầu từ vài trăm tới
vài ngàn vòng lặp [1], hay các bài toán phân tích độ
tin cậy bằng các mô phỏng Monte Carlo yêu cầu việc
tính toán lặp lại từ hàng ngàn lần tới hàng triệu lần [2]-
[4]. Ngoài ra, các chu trình ẩn cũng gây khó khăn
trong việc tính toán theo lý thuyết độ tin cậy khi cần
có những tính toán liên quan tới các phép tính đạo hàm,
ví dụ phương pháp độ tin cậy bậc nhất [5].
Gần đây, một số nghiên cứu đã tập trung xây dựng
các mô hình thay thế (surrogate model) nhằm giúp bài
toán tối ưu hay tính toán theo lý thuyết độ tin cậy trở
KHOA HỌC - CÔNG NGHỆ
59
SỐ 80 (11-2024)
nên dễ dàng và thuận tiện hơn [6], [7]. Sử dụng mô
hình thay thế, các chu trình ẩn sẽ được xấp xỉ thông
qua những mô hình toán học viết dưới dạng tường
minh giúp cho việc tính toán trở nên dễ dàng và thuận
tiện hơn. Ví dụ như các phép toán đạo hàm, vốn cần
thiết trong phương pháp độ tin cậy bậc nhất, sẽ được
tính toán dễ dàng hơn khi có hàm tường minh. Trong
các nghiên cứu trước, các mô hình thay thế thường
được xây dựng để tính toán các hệ số an toàn hay các
hàm trạng thái. Tuy nhiên, trong thực tế, ứng xử của
kết cấu như nội lực hay chuyển vị cũng thường được
quan tâm [7]. Trong nghiên cứu này, khả năng của
phương pháp bề mặt đáp ứng (RSM: Response surface
method) trong việc xây dựng các mô hình thay thế để
tính toán các ứng xử của kết cấu sẽ được nghiên cứu.
Nội dung phương pháp bề mặt đáp ứng sẽ được
trình bày cụ thể trong Mục 2. Mục 3 xem xét tính hiệu
quả và tính chính xác của các hàm bề mặt đáp ứng
thông qua 3 ví dụ. Các thảo luận và đánh giá cũng
được đưa ra trong Mục 3. Cuối cùng, các kết luận của
nghiên cứu được trình bay trong Mục 4.
2. Nội dung của phương pháp
Ý tưởng chung của phương pháp bề mặt đáp ứng
là xây dựng các mô hình dưới dạng tường minh nhằm
thay thế các tính toán thông qua chu trình ẩn vốn phức
tạp và yêu cầu nhiều thời gian cũng như công sức tính
toán. Để xây dựng được mô hình thay thế, trước hết,
một tập hợp các điểm đầu vào cần được thành lập,
thường được gọi là thiết kế thí nghiệm mẫu. Các giá
trị đầu ra tương ứng với tập mẫu thiết kế ở trên sẽ được
xác định thông qua các bài toán gốc. Sau đó, mối quan
hệ giữa các các điểm thí nghiệm đầu vào và đầu ra sẽ
được xấp xỉ thông qua các mô hình toán học.
2.1. Phương pháp thiết kế thí nghiệm
Để xây dựng các hàm thay thế, việc thiết kế thí
nghiệm là rất quan trọng. Thiết kế thí nghiệm tốt nhằm
đảm bảo tính chi tiết cũng như tính tổng thể của tập
mẫu nhằm giúp xây dựng hàm thay thế chính xác. Hai
phương pháp thiết kế thí nghiệm thường được sử dụng
là thiết kế Box-Behnken và thiết kế tâm xoay trung
tâm (CCD: Central composite design) [8]. Để dễ hình
dung, dưới đây trình bày cụ thể phương pháp thiết kế
CCD cho hai biến. Khi số lượng biến tăng lên, thiết kế
CCD được tiến hành tương tự.
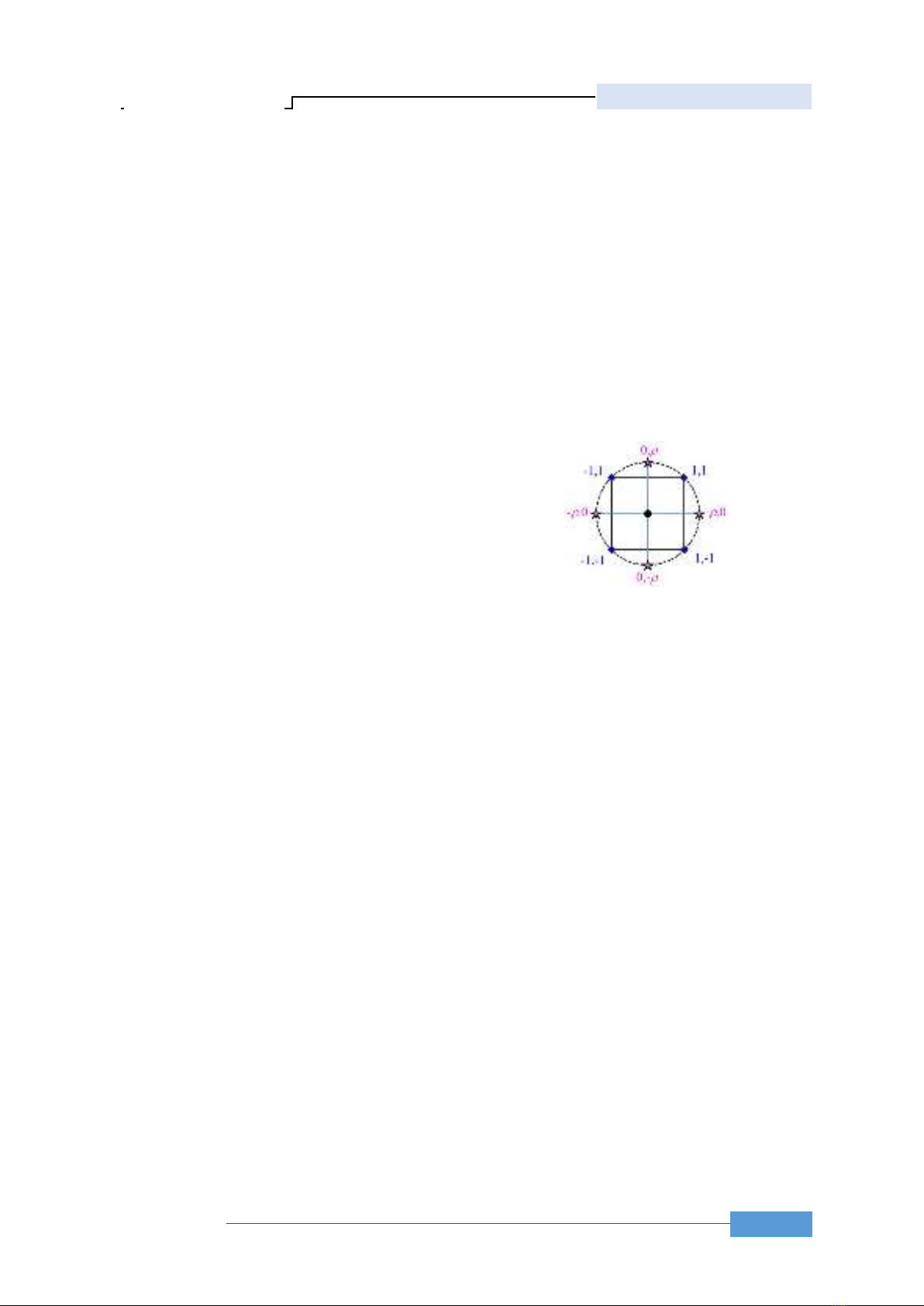
Gọi
X là điểm trung tâm, thường lấy là giá trị kỳ
vọng của các tham số, Hình 1 thể hiện thiết kế thí
nghiệm theo CCD cho trường hợp 2 biến. Gọi số
lượng biến là k, tập hợp các điểm mẫu thiết kế theo
CCD gồm 3: 2k điểm góc (factorial points) ký hiệu
bằng các hình thoi, 2k điểm sao (star points) ký hiệu
bằng các ngôi sao và 1 điểm trung tâm ký hiệu bằng
hình tròn đen trên Hình 1. Như vậy, tổng số lượng
điểm thí nghiệm thu được theo CCD là 2k +2k +1. Với
trường hợp 2 biến, tổng số mẫu thu được là 9 mẫu,
như thể hiện trên Hình 1. Lưu ý rằng, điểm trung tâm
thường được lấy tại các điểm kỳ vọng của các tham
số. Các điểm factorial thường được lấy tại các cận trên
và dưới của biến một khoảng bằng độ lệch chuẩn. Với
các điểm star, hệ số
được tính bằng căn bậc hai của
số lượng biến k (thường gọi là thiết kế tâm xoay tức là
đảm bảo tính xoay được, rotatability). Tổ hợp các
điểm kể trên đảm bảo phản ánh đầy đủ hiệu ứng tuyến
tính, phi tuyên, và tương tác giữa các tham số đầu vào
trong hàm bề mặt đáp ứng [8].
2.2. Xây dựng hàm bề mặt đáp ứng
Dựa trên kết quả thiết kế thí nghiệm ở Mục 2.1,
các ứng xử quan tâm sẽ được tính toán thông qua bài
toán ban đầu. Sau đó, mối quan hệ giữa tập hợp các
biến đầu vào thu được từ việc thiết kế thí nghiệm và
các biến đầu ra thu được từ các tính toán từ bài toán
gốc sẽ được xấp xỉ thông qua các hàm tường minh.
Các hàm thu được từ việc xấp xỉ thường được gọi là
hàm bề mặt đáp ứng (response surface function).
Trong các bài toán kỹ thuật, hàm đa thức (thường tới
bậc hai) và hàm mũ là các dạng hàm thường được áp
dụng [7]. Trong nghiên cứu này hàm đa thức bậc nhất
và bậc hai sẽ được sử dụng. Các phương trình (1a),
(1b), và (1c) lần lượt thể hiện dạng hàm đa thức bậc
nhất, bậc hai rút gọn, và bậc hai đầy đủ. Trong các
phương trình (1), y(l), y(2,r), và y(2,f) lần lượt thể hiện các
hàm bề mặt đáp ứng xác định theo các mô hình tuyến
tính, đa thức bậc hai rút gọn, và đa thức bậc hai đầy
đủ.
0,
={
i},
={
i},
={
i} là các hệ số cần xác
định trong quá trình xây dựng hàm bề mặt đáp ứng.
Căn cứ vào tập hợp mẫu ở trên, các hệ số này sẽ được
xác định bằng cách tối ưu sao cho sai số của hàm bề
mặt đáp ứng là nhỏ nhất.
( )

=
=+
0
1
k
l
ii
i
yx
(1a)
Hình 1. Thiết kế mẫu cho hai biến theo CCD.
KHOA HỌC - CÔNG NGHỆ
60
SỐ 80 (11-2024)
TẠP CHÍ ISSN: 1859-316X
KHOA HỌC CÔNG NGHỆ HÀNG HẢI
JOURNAL OF MARINE SCIENCE AND TECHNOLOGY
( )
==
= + +

2, 2
0
11
kk
r
i i i i
ii
y x x
(1b)
( )
−
= = = = +
= + + +
1
2, 2
0
1 1 1 1
k k k k
f
i i i i ij i j
i i i j i
y x x x x
(1c)
3. Các ví dụ tính toán
Trong mục này, nội dung phương pháp RSM trình
bày trong Mục 2 sẽ được áp dụng cho ba ví dụ. Ví dụ
thứ nhất xem xét bài toán kết cấu dàn phẳng tĩnh định,
nội lực trong thanh dàn và chuyển vị lớn nhất của kết
cấu sẽ được xem xét. Sau đó, liên kết sẽ được thêm
vào để biến kết cấu dàn trở thành siêu tĩnh trong Ví dụ
2, tải trọng cũng được thêm vào để hệ kết cấu trở nên
phức tạp hơn. Cuối cùng, Ví dụ 3 xét một khung phẳng
siêu tĩnh chịu tải trọng phân bố đều trên dầm. Mô men
và chuyển vị lớn nhất tại giữa dầm sẽ được xem xét.
Để đánh giá tính chính xác của các hàm xấp xỉ xây
dựng được từ RSM, tập hợp mẫu gồm các tham số đầu
vào sẽ được tạo ngẫu nhiên thông qua các mô phỏng
MCS. Sau đó, các tập ngẫu nhiên sẽ được đưa vào
hàm xấp xỉ và hàm thực của từng bài toán. Hệ số xác
định (coefficient of determination, R2) sẽ được dùng
để đánh giá sự chính xác của các hàm bề mặt đáp ứng.
3.1. Ví dụ 1 - Kết cấu dàn giản đơn
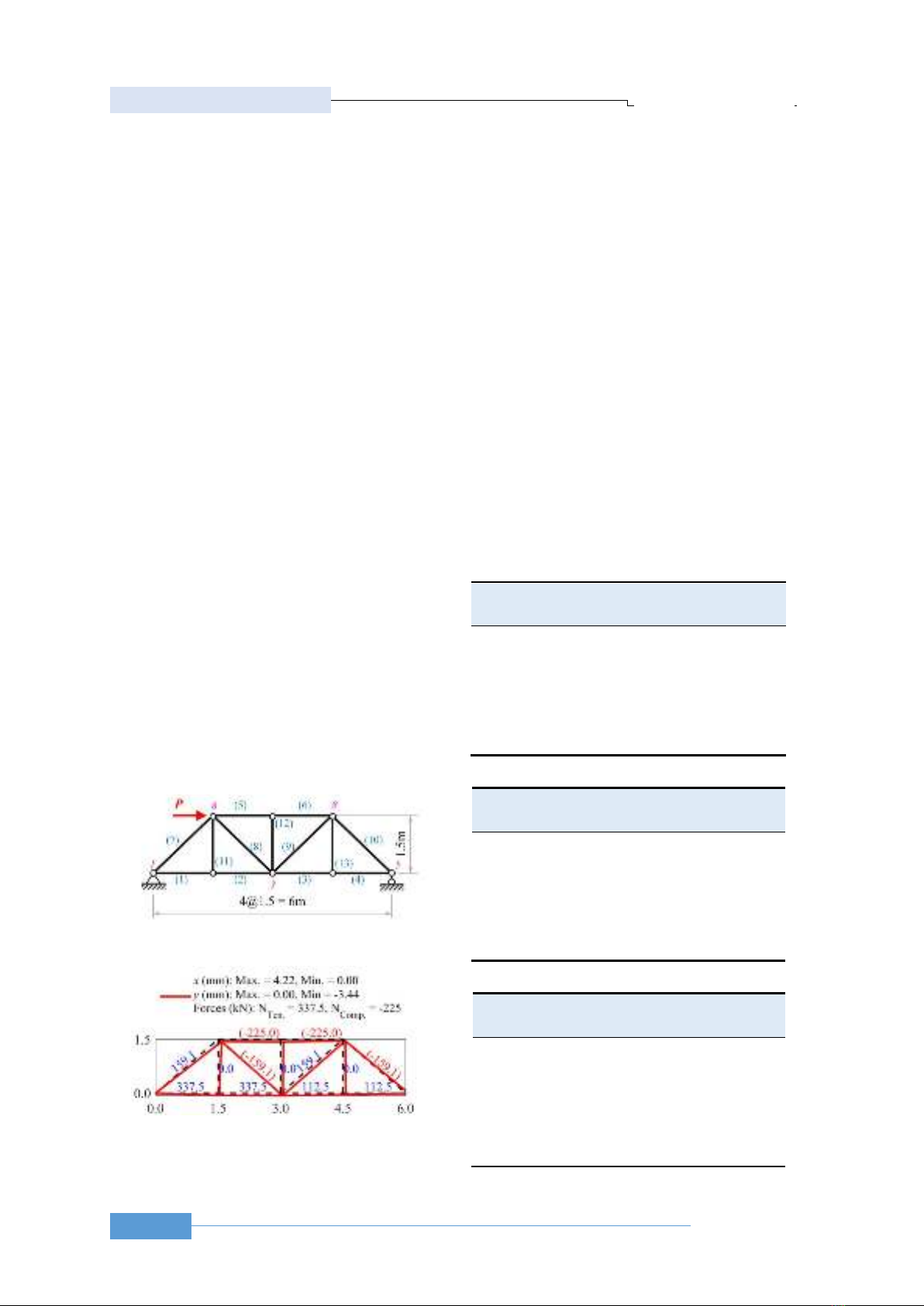
Trong ví dụ này, một kết cấu dàn Pratt trên Hình 2
được nghiên cứu. Kết cấu dàn gồm 13 thanh tiết diện
tròn, diện tích A=20cm2 chịu lực P=20kN theo
phương ngang đặt tại nút 6 ở biên trên dàn.
Chương trình FEM-Truss xây dựng từ nghiên cứu
trước [3] được sử dụng để tính toán lực dọc (N) và
chuyển vị nút (x, y). Kết quả được thể hiện trên Hình
2. Hình 2 cho thấy, nội lực kéo lớn nhất xuất hiện
trong thanh 1 và thanh 2, trong khi lực nén lớn nhất ở
thanh 5 và thanh 6. Chuyển vị ngang lớn nhất tại nút
đặt lực (x6) và nội lực thanh 1 và 5 (N1 và N5) sẽ được
tính toán thông qua RSM trình bày trong Mục 2.
Trong ví dụ này, hai tham số gồm diện tích thanh
A và tải trọng P sẽ được coi là biến bất định với hệ số
COV lần lượt là 0,05 và 0,25. Do đó, 5 điểm lấy mẫu
sẽ được thực hiện khi dùng hàm xấp xỉ dạng bậc hai.
Ngoài 5 điểm lấy mẫu ở trên, 4 điểm khác cần lấy
thêm để xây dựng mô hình bậc hai đầy đủ.
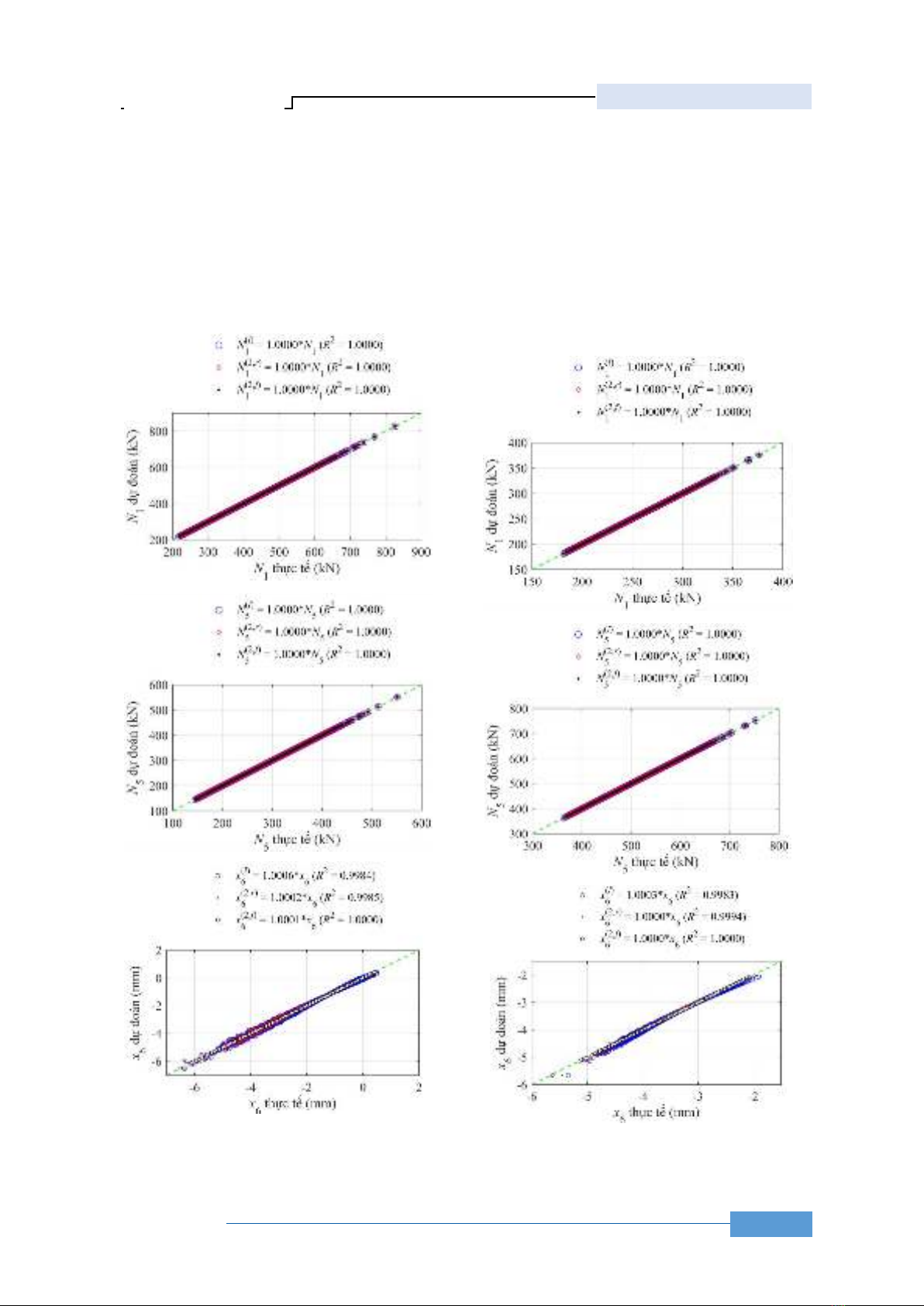
Kết quả tính toán các hệ số của hàm bề mặt đáp
ứng lần lượt được ghi lại trong Bảng 1, 2 và 3 cho lực
nén, lực kéo và chuyển vị ngang lớn nhất. Sử dụng các
hàm này để dự đoán cho 100,000 mẫu ngẫu nhiên tạo
được từ MCS. Hình 3 so sánh các giá trị dự đoán bằng
3 mô hình với kết quả tính bằng FEM-Truss.
Hình 1. Ví dụ 1 - Kết cấu dàn tĩnh định
Hình 2. Ứng xử kết cấu dàn trong Ví dụ 1
Bảng 1. Hệ số của hàm xấp xỉ cho lực nén N5
Tham số
Bậc nhất
Bậc hai
rút gọn
Bậc hai
đầy đủ
0
1.17E-11
120
-7.24E-10
A
-1.18E-11
0
1.45E-09
P
225
0
225
A2
−
-5.34E-12
-7.31E-10
P2
−
105
-1.76E-12
A P
−
−
8.18E-12
Bảng 2. Hệ số của hàm xấp xỉ cho lực kéo N1
Tham số
Bậc nhất
Bậc hai
rút gọn
Bậc hai
đầy đủ
0
-3.03E-11
180.52
-2.97E-10
A
2.89E-11
0
6.76E-10
P
337.5
0
337.5
A2
−
1.50E-11
-3.81E-10
P2
−
156.98
-1.85E-12
A P
−
−
8.05E-11
Bảng 3. Hệ số của hàm xấp xỉ cho chuyển vị ngang x6
Tham số
Bậc nhất
Bậc hai
rút gọn
Bậc hai
đầy đủ
0
-3.27
-1.71
-6.25
A
6.22
0
18.28
P
-2.96
0
-8.82
A2
−
3.08
-9.04
P2
−
-1.38
3.51E-04
A P
−
−
5.82
KHOA HỌC - CÔNG NGHỆ
61
SỐ 80 (11-2024)
Hệ số xác định (determination coeficient R2) thể
hiện mức độ tương quan giữa hai bộ kết quả tính cũng
được tổng hợp trên Hình 3. Kết quả tính toán trên
Hình 3 cho thấy ba mô hình đa thức cho các nội lực
N1 và N5 rất tương đồng với kết quả tính từ FEM. Tuy
nhiên, với chuyển vị x6, các mô hình bậc nhất và bậc
hai rút gọn cho kết quả tương đối chính xác. Tuy nhiên,
mô hình đa thức bậc 2 đầy đủ cho kết quả gần như
tương đồng với kết quả từ FEM (sai số 0,01%).
3.2. Ví dụ 2 - Kết cấu dàn siêu tĩnh
Ví dụ 1 ở trên xem xét kết cấu dàn tĩnh định chịu
lực theo phương ngang. Trong ví dụ này, kết cấu dàn
ở trên được thêm liên kết ở gối phải để hệ trở thành hệ
siêu tĩnh. Ngoài ra, một tải trọng theo phương thẳng
đứng cũng được thêm vào nút 6 để tăng tính phức tạp.
Các dạng hàm sẽ được khảo sát khi tính toán ứng xử
của kết cấu dàn. Hình 4 trình bày kết quả dự đoán lực
dọc trong thanh chịu kéo (N1) và nén lớn nhất (N5) cho
100,000 mẫu ngẫu nhiên.
Hình 3. So sánh kết quả tính toán cho Ví dụ 1
Hình 4. So sánh kết quả tính toán cho Ví dụ 2
KHOA HỌC - CÔNG NGHỆ
62
SỐ 80 (11-2024)
TẠP CHÍ ISSN: 1859-316X
KHOA HỌC CÔNG NGHỆ HÀNG HẢI
JOURNAL OF MARINE SCIENCE AND TECHNOLOGY
Tương tự Ví dụ 1, kết quả tính toán trên Hình 4
cho thấy ba mô hình đều cho kết quả nội lực tương
đồng với FEM. Với chuyển vị x6, mô hình bậc hai đầy
đủ vẫn cho kết quả chính xác nhất.
Từ kết quả của Ví dụ 1 và 2 có thể thấy nội lực
thanh dàn hoàn toàn có thể xấp xỉ bằng mô hình bậc
nhất nhưng chuyển vị nút cần phải được xấp xỉ bằng
đa thức bậc 2 đầy đủ bất kể kết cấu dàn là tĩnh định
hay siêu tĩnh. Điều này tương thích với lý thuyết rằng
nội lực thanh dàn chỉ phụ thuộc vào tải trọng tác dụng,
còn chuyển vị không chỉ phụ thuộc vào diện tích thanh
hay tải trọng mà còn cả tương tác giữa các thành phần
này vì vậy đa thức bậc hai rút gọn (vốn bỏ thành phần
tương tác giữa các tham số) sẽ không đưa ra kết quả
chính xác. Lưu ý rằng, 9 mẫu thử đủ để xây dựng mô
hình đa thức bậc hai đầy đủ giúp thay thế bài toán kết
cấu dàn. Từ đó, việc tính toán lặp lại hàng triệu lần
cần thiết trong tính toán theo lý thuyết độ tin cậy sẽ
trở nên dễ dàng và thuận tiện hơn.
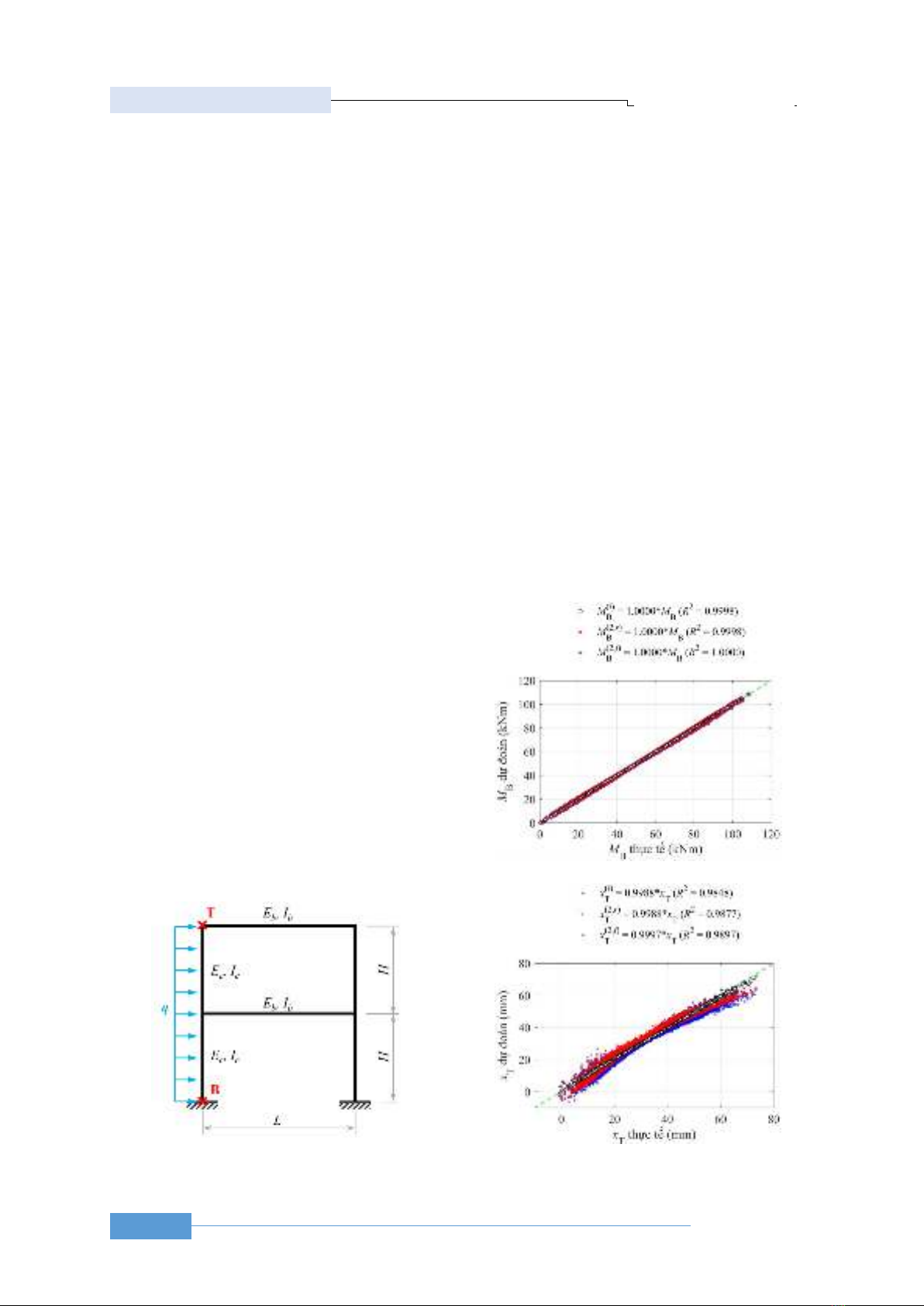
3.3. Ví dụ 3 - Khung phẳng siêu tĩnh
Với kết cấu khung siêu tĩnh, nội lực và chuyển vị
của khung không chỉ phụ thuộc vào tải trọng mà còn
cả độ cứng của khung (độ cứng của dầm và cột). Do
đó, khả năng xấp xỉ của các hàm bề mặt đáp ứng sẽ
được xét xét trong mục này. Một kết cấu khung phẳng
hai tầng một nhịp có liên kết ngàm tại chân cột như
Hình 5 sẽ được nghiên cứu.
Các cột có tiết diện vuông cạnh 20cm còn dầm có
tiết diện chữ nhật rộng 20cm và cao 30cm. Chiều cao
tầng H và chiều dài nhịp L lần lượt là 3m và 5m. Tải
trọng q = 12kN/m phân bố đều trên toàn bộ chiều cao
cột. Dầm và cột được chế tạo cùng vật liệu bê tông có
mô đun đàn hồi E = 29944MPa. Sử dụng phương pháp
phần tử hữu hạn, mô men lớn nhất tại chân cột trái
(MB) và chuyển vị ngang lớn nhất tại đỉnh cột xT lần
lượt tính được là tính được là 53,3kNm và 3,03cm.
Các tham số bất định trong ví dụ này gồm có kích
thước các cạnh của tiết diện dầm và cột (4 biến) tuân
theo phân phối chuẩn với hệ số biến thiên là 5%, và
tải trọng q cũng tuân theo phân phối chuẩn với hệ số
biến thiên là 25%. Như vậy bài toán gồm 5 tham số,
khi đó, số lượng mẫu cần thiết để xây dựng mô hình
bậc nhất và bậc hai rút gọn là 11 mẫu, nhưng mô hình
bậc hai đầy đủ cần tới 43 mẫu (thêm 25 = 32 mẫu cho
các điểm sao) để xác định các hệ số. Tức là mô hình
bậc hai đầy đủ yêu cầu số lượng mẫu gấp gần 4 lần so
với mô hình bậc hai rút gọn. Tương tự như hai ví dụ
trước, ba mô hình trong công thức (1) sẽ được sử dụng
để xấp xỉ MB và xT.
Kết quả so sánh mô men chân cột và chuyển vị
ngang ở đỉnh cột theo ba mô hình và kết quả tính theo
công thức chính xác cho 100,000 mẫu thử phát sinh
theo MCS được thể hiện trong Hình 6. Kết quả trên
Hình 6 cho thấy, với MB, các mô hình bậc nhất và bậc
hai rút gọn đều cho kết quả chính xác. Đặc biệt, kết
quả tính theo mô hình bậc hai đầy đủ cho kết quả
chính xác với kết quả tính theo công thức (2).
Hình 5. Ví dụ 3 - Khung phẳng siêu tĩnh
Hình 6. So sánh kết quả tính toán cho Ví dụ 3