WWW.VNMATH.COM
L I NÓI Đ UỜ Ầ
Các em h c sinh thân m n!ọ ế
Tài li u “Ph ng pháp gi i toán HÌNH H C KHÔNG GIAN”ệ ươ ả Ọ
giúp
các em n m v ng các ph ng pháp ch ng minh hình h c khôngắ ữ ươ ứ ọ
gian.
Trong tài li u này g m có:ệ ồ
+ Các ph ng pháp gi i toán.ươ ả
+ 44 bài t p ôn thi t t nghi p THPT.ậ ố ệ
+ 100 bài t p luy n thi Đ I H C &CAO Đ NG. ậ ệ Ạ Ọ Ẳ
Đ s d ng tài li u này,tr c khi đ n h c trung tâm,các emể ử ụ ệ ướ ế ọ ở
ph i ả
đ c kĩ các ph ng pháp gi i toán,ọ ươ ả các ví d , làm các bài t p ôn thiụ ậ
t t ố
nghi p tr c,còn các bài t p luy n thi Đ i h c m c đ khó cácệ ướ ậ ệ ạ ọ ở ứ ộ
em
ph i quy t tâm m i gi i đ c.N u có v n đ các em ch a hi u th yả ế ớ ả ượ ế ấ ề ư ể ầ
s ẽ
giúp các em gi i quy t thêm l p.ả ế ở ớ
Quá trình biên so n tài li u này không tránh kh i sai sót.ạ ệ ỏ
R t mong có s góp ý t các b c ph huynh và các em h c sinhấ ự ừ ậ ụ ọ .
CHÚC CÁC EM THÀNH Đ T!Ạ
Chuyên đ hình h c ề ọ -Trang 1- Biên so n Nguyạ ễn
Văn Xê
WWW.VNMATH.COM
CÁC PH NG PHÁP CH NG MINH HÌNH H CƯƠ Ứ Ọ
I.Ph ng pháp ch ng minh đ ng th ng song song m t ph ngươ ứ ườ ẳ ặ ẳ :
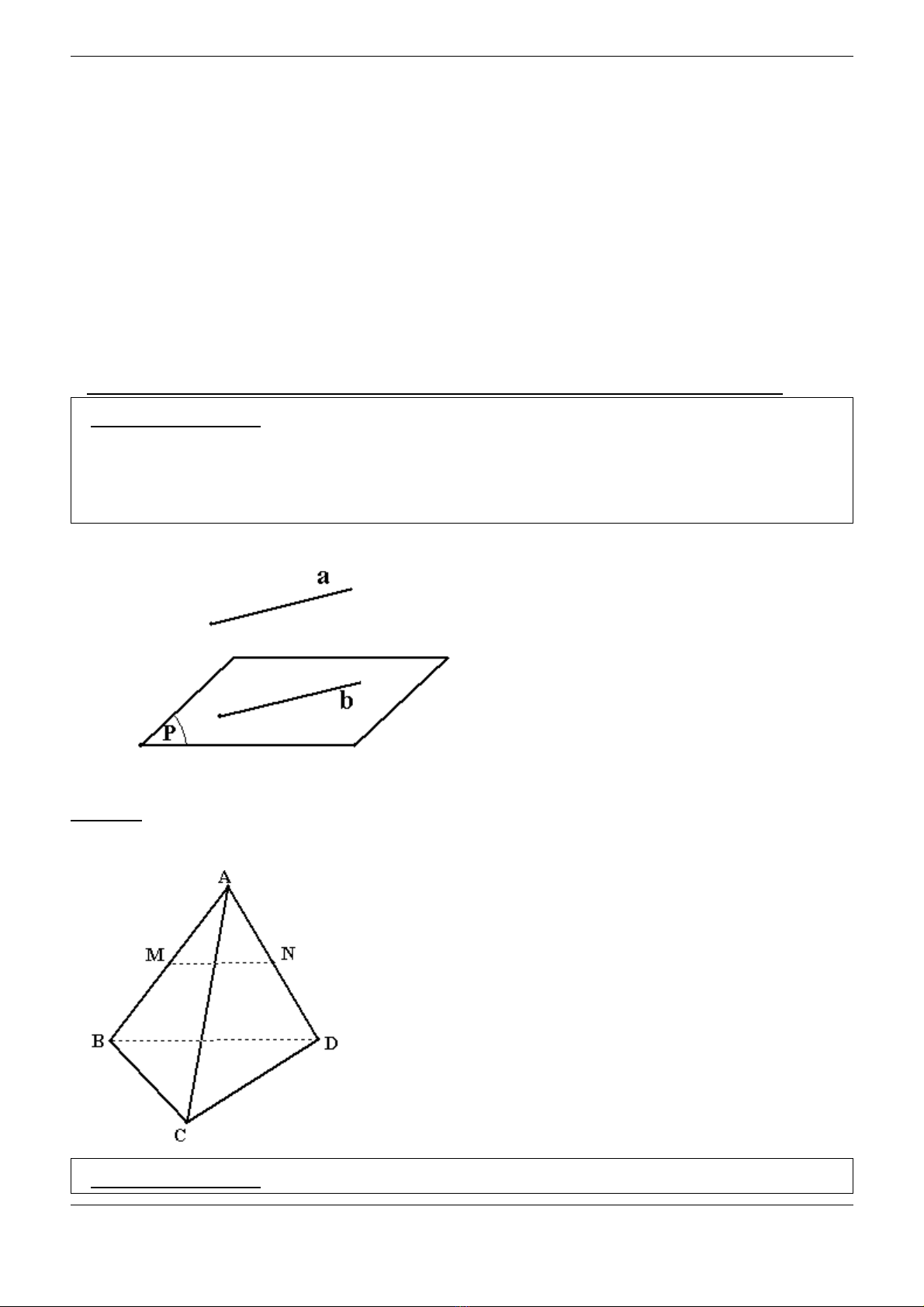
♦Ph ng pháp1ươ :
Mu n ch ng minh đ ng th ng song song v i m t ph ng taố ứ ườ ẳ ớ ặ ẳ
ch ng minh đ ng th ng đó không n m trong m t ph ng và songứ ườ ẳ ằ ặ ẳ
song v i m t đ ng th ng nào đó n m trong m t ph ngớ ộ ườ ẳ ằ ặ ẳ .
a // b
b (P) a //(P)
a (P)
� �
�
Ví d :ụ Cho t di n ABCD.G i M,N l n l t là trung đi m c a AB, AD.ứ ệ ọ ầ ượ ể ủ
Ch ng minh MN song song v i m t ph ng (BCD).ứ ớ ặ ẳ
Gi i:ả Trong tam giác ABD có:
M trung đi m c a ABể ủ
N trung đi m c a AD.ể ủ
Nên MN là đ ng trung bình c a ườ ủ
tam giác ABD
Do đó MN // BD
Mà BD
(BCD)
MN
(BCD)
V y MN // (BCD).ậ
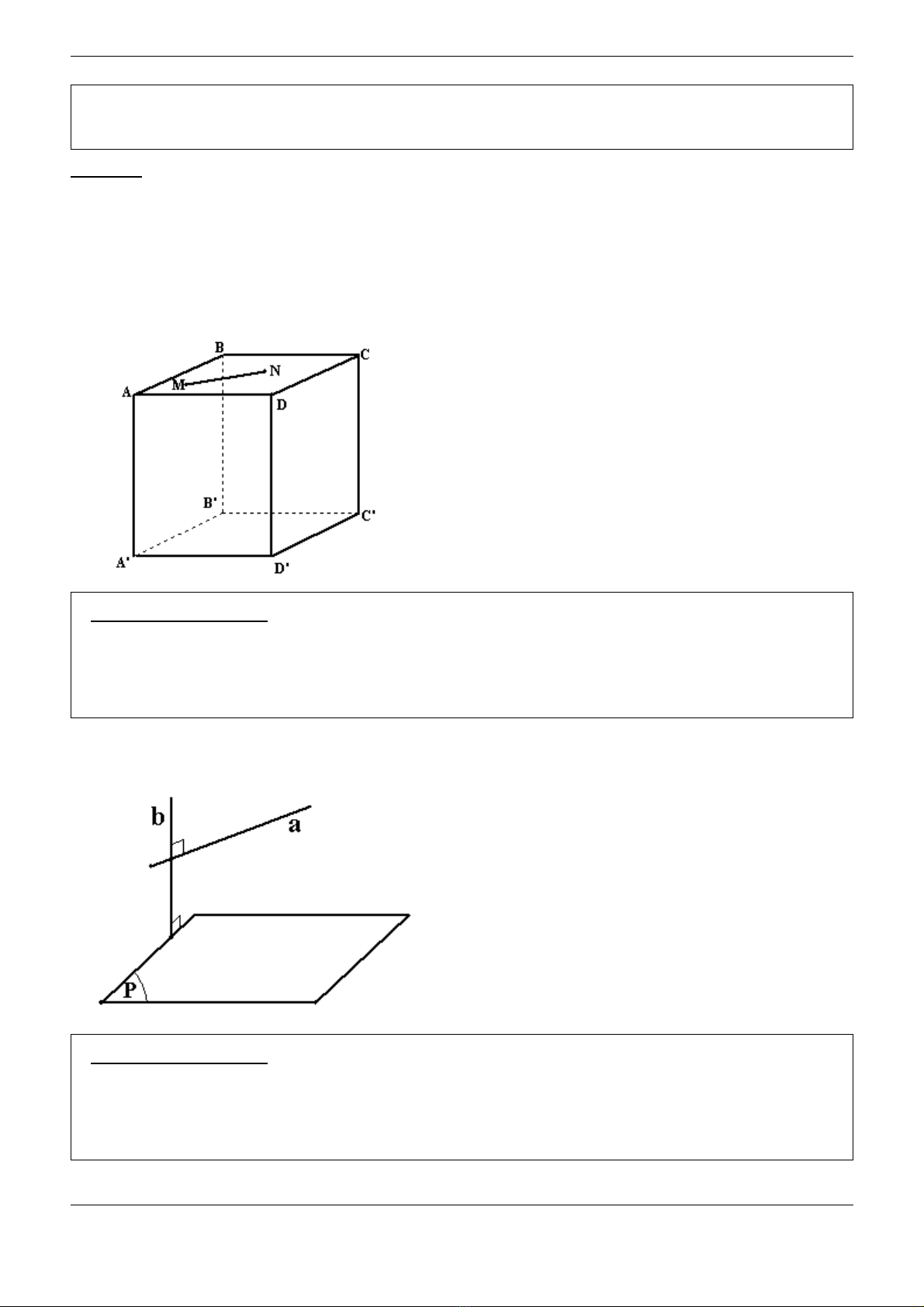
♦Ph ng pháp2ươ :
Chuyên đ hình h c ề ọ -Trang 2- Biên so n Nguyạ ễn
Văn Xê
WWW.VNMATH.COM
Mu n ch ng minh đ ng th ng a song song m t ph ng (P) taố ứ ườ ẳ ặ ẳ
ch ng minh đ ng th ng a n m trong m t ph ng (Q) mà (Q) // (P)ứ ườ ẳ ằ ặ ẳ
Ví d :ụ Cho hình h p ABCD.A’B’C’D’. M; N tuỳ ý trên m t ph ngộ ặ ẳ
(ABCD).
Ch ng minh MN // m t ph ng (A’B’C’D’).ứ ặ ẳ
(ABCD) //(A'B'C'D')
MN (ABCD)
MN //(A'B'C'D')
�
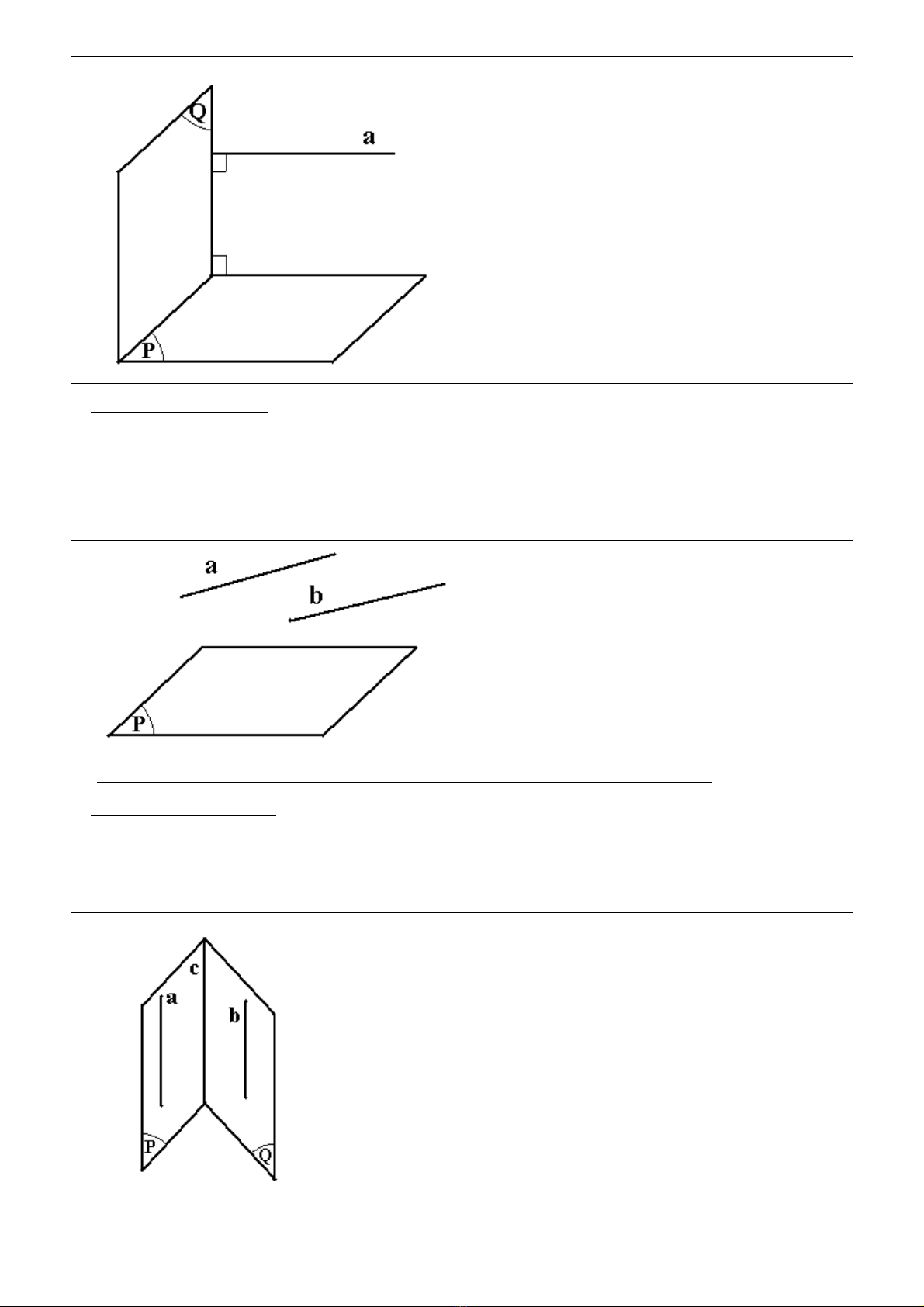
♦Ph ng pháp 3ươ :
Mu n ch ng minh đ ng th ng a song song m t ph ng (P), taố ứ ườ ẳ ặ ẳ
ch ng minh đ ng th ng a và m t ph ng (P) không có đi m chungứ ườ ẳ ặ ẳ ể
cùng vuông góc v i m t đ ng th ng b.ớ ộ ườ ẳ
♦Ph ng pháp 4ươ :
Mu n ch ng minh đ ng th ng a song song m t ph ng (P), taố ứ ườ ẳ ặ ẳ
ch ng minh đ ng th ng a và m t ph ng (P) không có đi m chungứ ườ ẳ ặ ẳ ể
cùng vuông góc v i m t m t ph ng (Q).ớ ộ ặ ẳ
Chuyên đ hình h c ề ọ -Trang 3- Biên so n Nguyạ ễn
Văn Xê
WWW.VNMATH.COM
♦Ph ng pháp 5ươ :
Mu n ch ng minh đ ng th ng a song song m t ph ng (P), taố ứ ườ ẳ ặ ẳ
ch ng minh đ ng th ng a song song vứ ườ ẳ ới đường th ẳng b mà
đ ng th ng b song song vườ ẳ i m t ph ng (P)(a và (P) không có đi mớ ặ ẳ ể
chung)
II.Ph ng pháp ch ng minh hai đ ng th ng song song:ươ ứ ườ ẳ
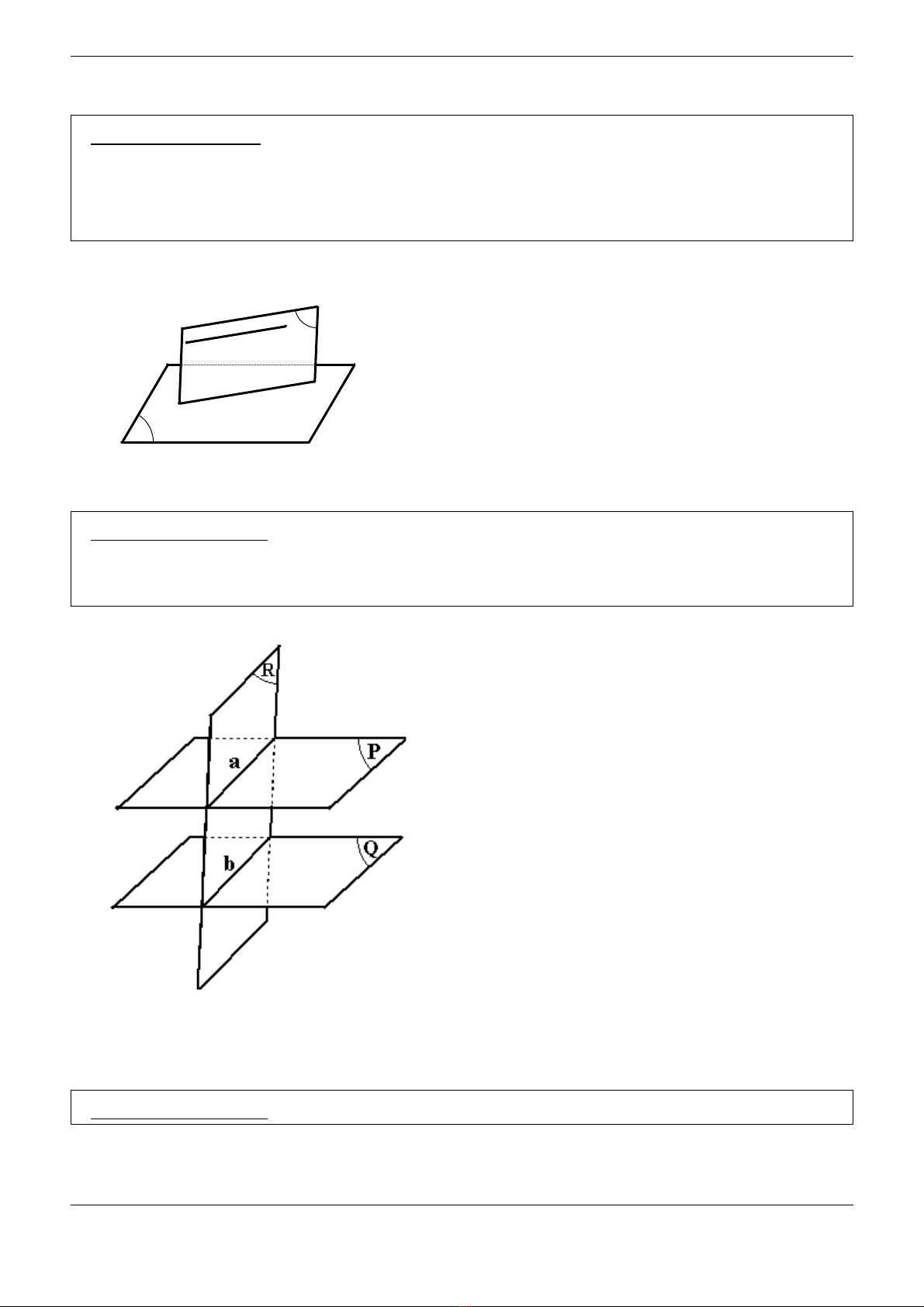
♦Ph ng pháp 1:ươ
S d ng đ nh lý: ử ụ ị N u hai m t ph ng c t nhau l n l t đi quaế ặ ẳ ắ ầ ượ
hai đ ng th ng song song thì giao tuy n c a chúng song song v iườ ẳ ế ủ ớ
hai đ ng th ng đó(ho c trùng v i m t trong hai đ ng th ng đó).ườ ẳ ặ ớ ộ ườ ẳ
a // b
a (P) c // a // b
b (Q)
(P) (Q) c
�
=�
Chuyên đ hình h c ề ọ -Trang 4- Biên so n Nguyạ ễn
Văn Xê
WWW.VNMATH.COM
♦Ph ng pháp2ươ :
S d ng đ nh lýử ụ ị : N u đ ng th ng a song song m t ph ng (P) thìế ườ ẳ ặ ẳ
m i m t ph ng (Q) ch a a mà c t m t ph ng (P) thì c t theo giaoọ ặ ẳ ứ ắ ặ ẳ ắ
tuy n b song song v i đ ng th ng a. ế ớ ườ ẳ
(P) // a
a (Q) b // a
(P) (Q) b
� �
�
=�
♦Ph ng pháp 3ươ :
S d ng đ nh lý: ử ụ ị N u m t ph ng (R) c t hai m t ph ng songế ặ ẳ ắ ặ ẳ
song (P) và (Q) l n l t theo hai giao tuy n a và b thì a//bầ ượ ế .
(P) //(Q)
(R) (P) a a // b
(R) (Q) b
=� �
�
=�
♦Ph ng pháp 5ươ :
Chuyên đ hình h c ề ọ -Trang 5- Biên so n Nguyạ ễn
Văn Xê
Q
P