Nguyễn Hồng Nam, 2007
21
Phương pháp trọng lực
Chú ý:
•Đối với vật liệu không thoát nước
Chọn Ignore undrained behaviour trong Phase 1 để
ngăn chặn áp lực lỗrỗng tăng thêm không hợp lý
•Phương pháp Ko đã được tạo từ trước
Trong giai đoạn ban đầu, làm lại phương pháp Kovới
ΣMweight=0 để đặt lại giá trịứng suất ban đầu bằng 0
Nguyễn Hồng Nam, 2007
22
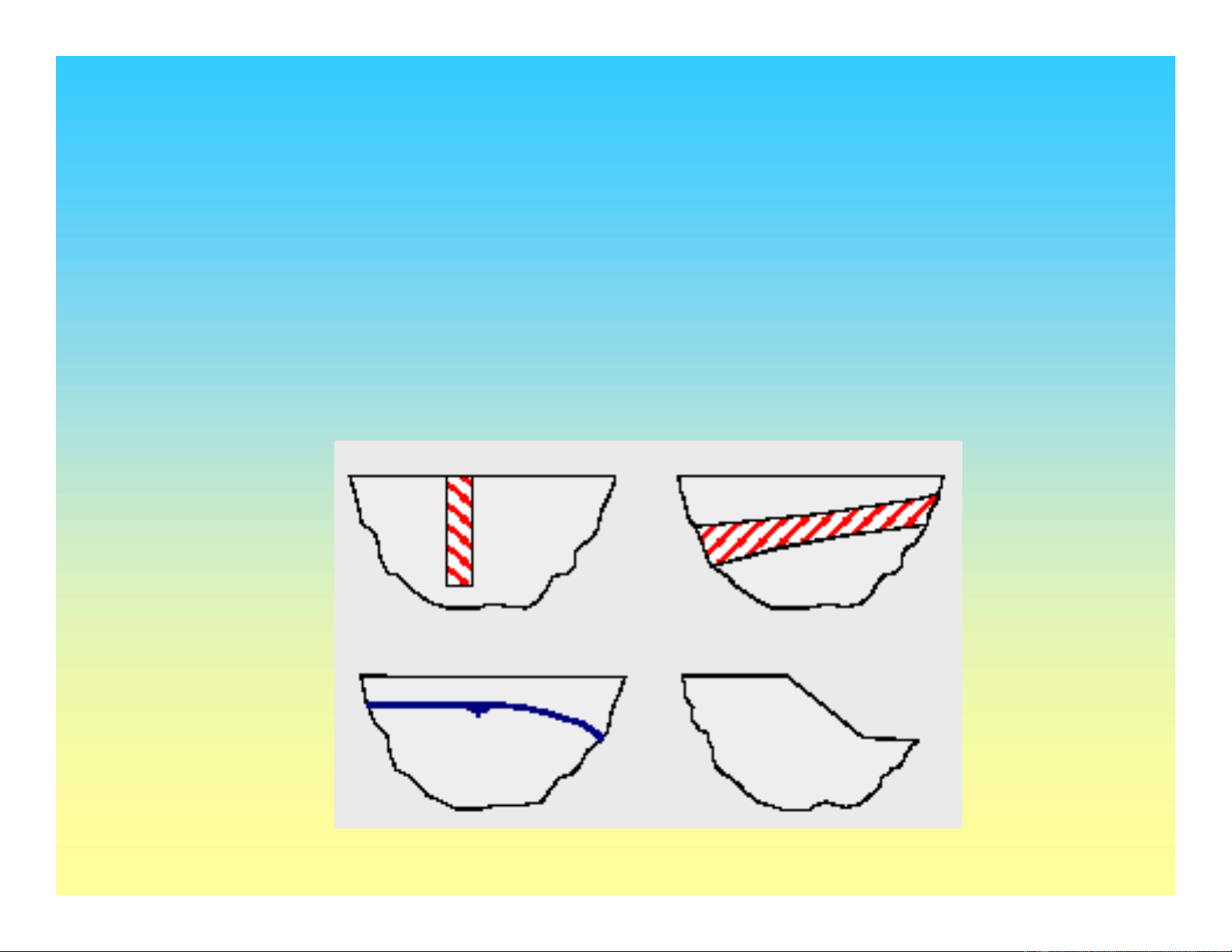
Phương pháp trọng lực
•Phương pháp trọng lực nên sửdụng trong các
trường hợp dưới đây, thay thế phương pháp Ko.
Nguyễn Hồng Nam, 2007
23
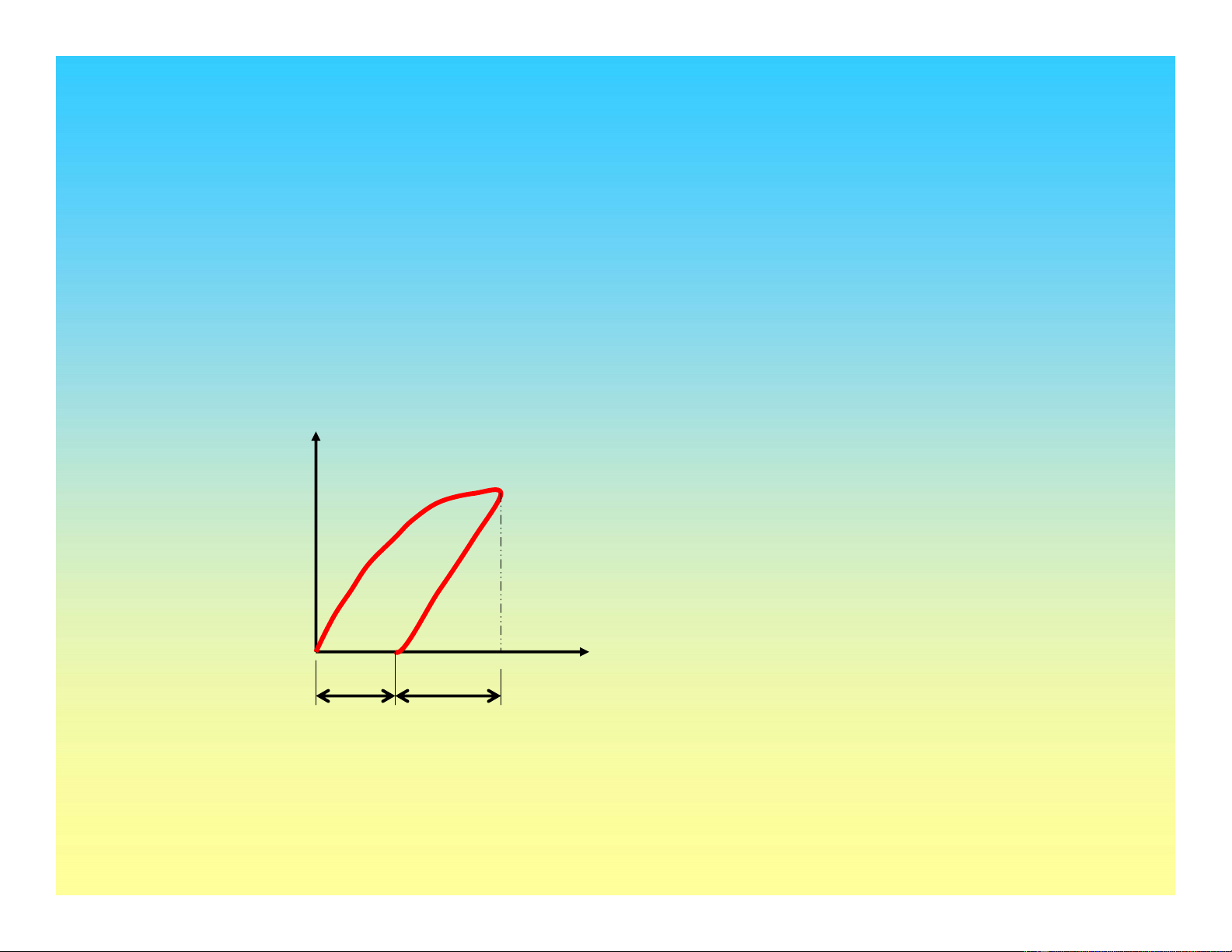
Biến dạng đàn hồi và biến dạng dẻo
εpεe
σ
ε
pe
ε
ε
ε
+
=
Trong ®ã,
εe: biÕn d¹ng ®µn håi,
εp: biÕn d¹ng dÎo,
ε: biến dạng tổng.
Nguyễn Hồng Nam, 2007
24
Đàn hồi đẳng hướng
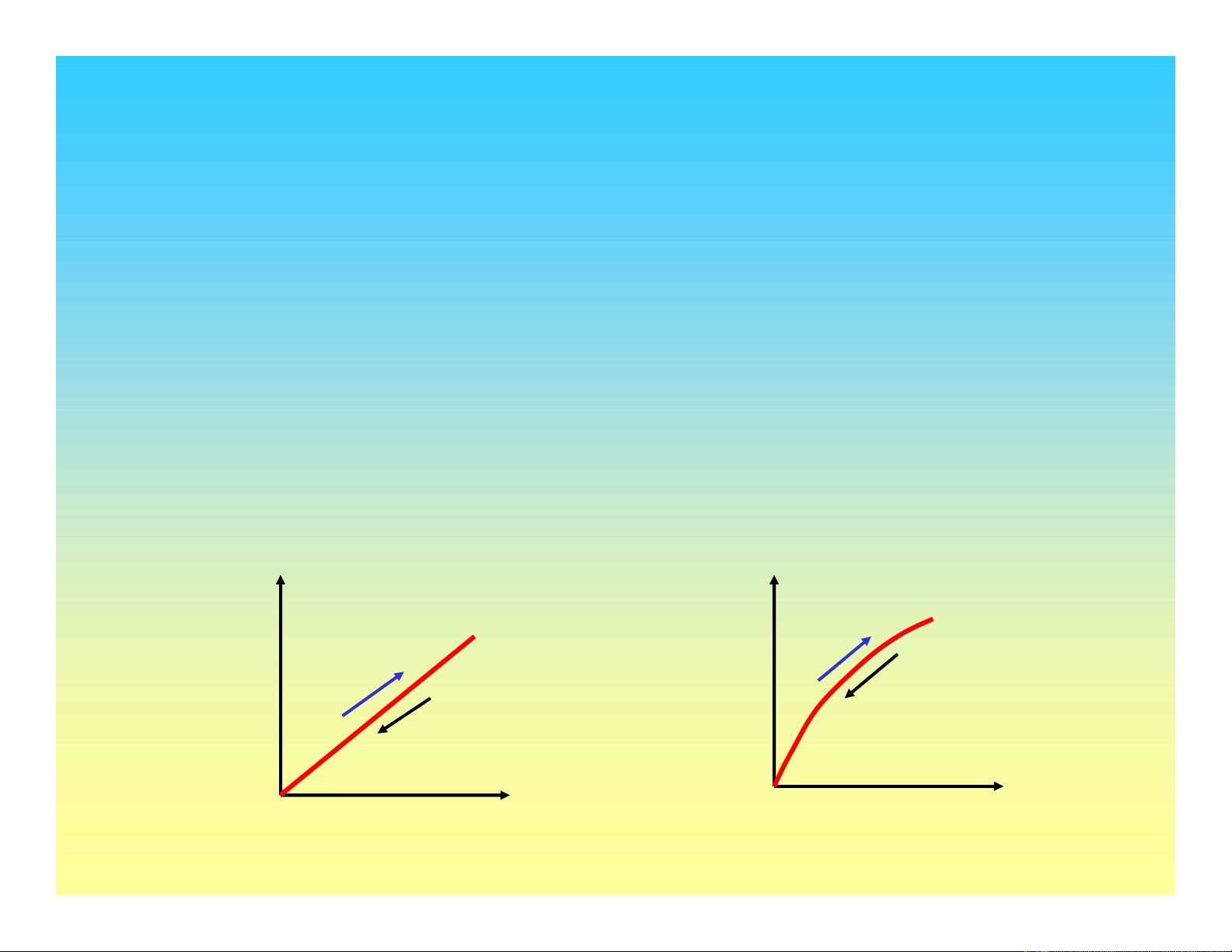
• Quan hệứng suất -biến dạng là tuyến tính hoặc phi tuyến
•Khi chất tải rồi dỡtải, vật liệu trởvềnguyên trạng thái ban đầu
•Biến dạng phụthuộc độ tăng ứng suất
•Lực tác dụng nhỏ hơn tải trọng giới hạn (giới hạn làm việc)
•Lựa chọn E, v ?
σ
ε
σ
ε
Tuyến tính Phi tuyến
Nguyễn Hồng Nam, 2007
25
Mô hình đàn hồi tổng quát
{
}
[
]
{
}
σ
ε
D
=
•Ma trận D bao gồm: 36 pt (tổng quát), 21 phần tử (đối xứng),13 phần tử
(đối xứng qua 1 mặt phẳng), 9 phần tử (đối xứng qua 3 mặt phẳng), 5
phần tử (đối xứng trục)
Đàn hồi đẳng hướng, 2 trong 4 tham sốsau là độc lập: E, ν, K, G
Định luật Hooke
=
zx
yz
xy
z
y
x
zx
yz
xy
z
y
x
DDDDDD
DDDDDD
DDDDDD
DDDDDD
DDDDDD
DDDDDD
τ
τ
τ
σ
σ
σ
γ
γ
γ
ε
ε
ε
666564636261
565554535251
464544434241
363534333231
262524232221
161514131211
Biến
dạng
ứng
suất