Nguyễn Hồng Nam, 2007
26
Biến dạng dẻo
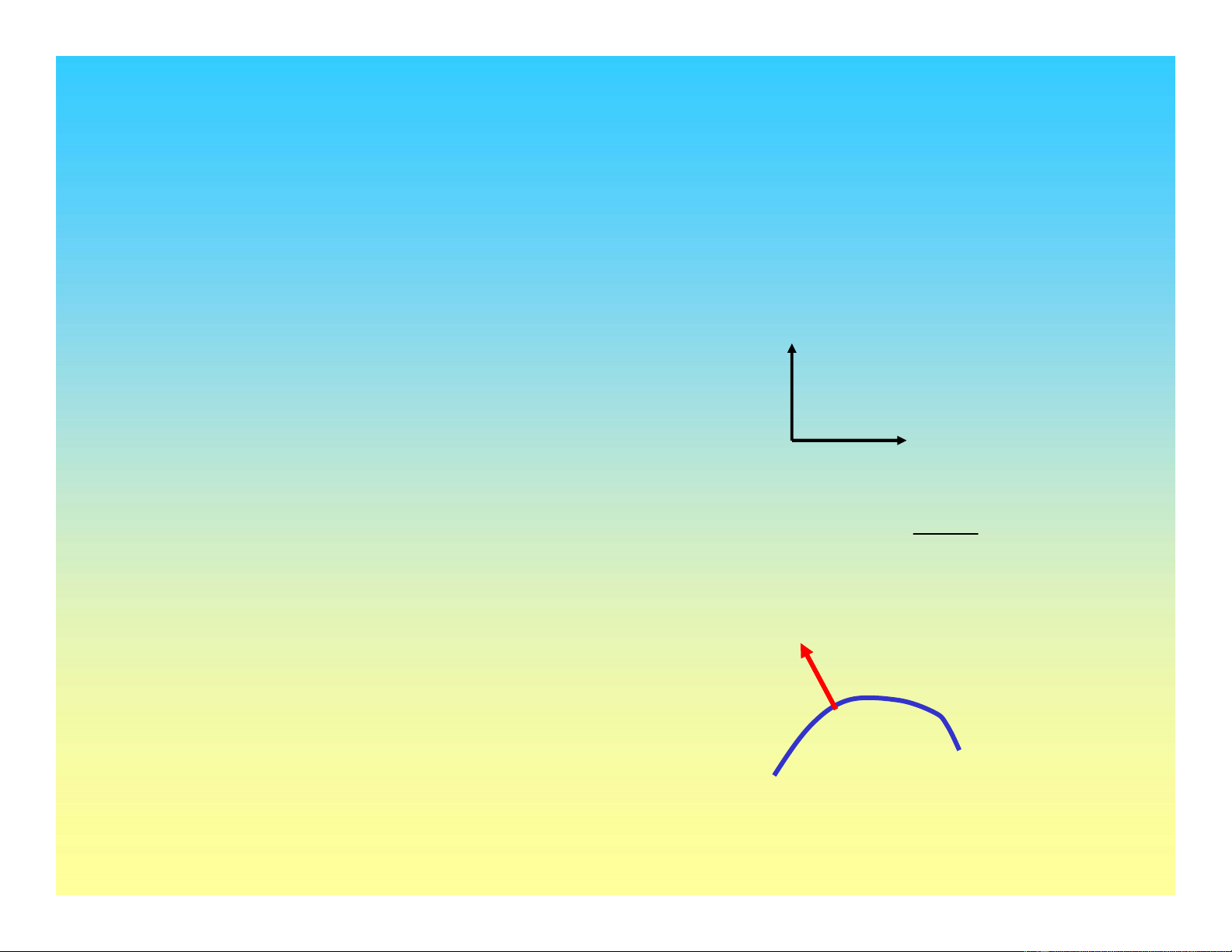
•Sự đồng hướng (coaxiality):
Các trục chính cuả độ tăng ứng suất
và độ tăng biến dạng chính cùng
phương
•Hàm thế năng dẻo g(Plastic
potential function) Sự tăng biến dạng
dẻo độc lập với tỷsốhoặc độ lớn của
độ tăng ứng suất, nhưng phụthuộc
trạng thái ứng suất
•Vectơ độ tăng biến dạng dẻovuông
góc mặt cong g
ij
p
ij
g
d
σ
λε
∂
∂
=
&
g(σij)=const
ij
p
ε
&
33,
ε
σ
&
&
11,
ε
σ
&
&
Nguyễn Hồng Nam, 2007
27
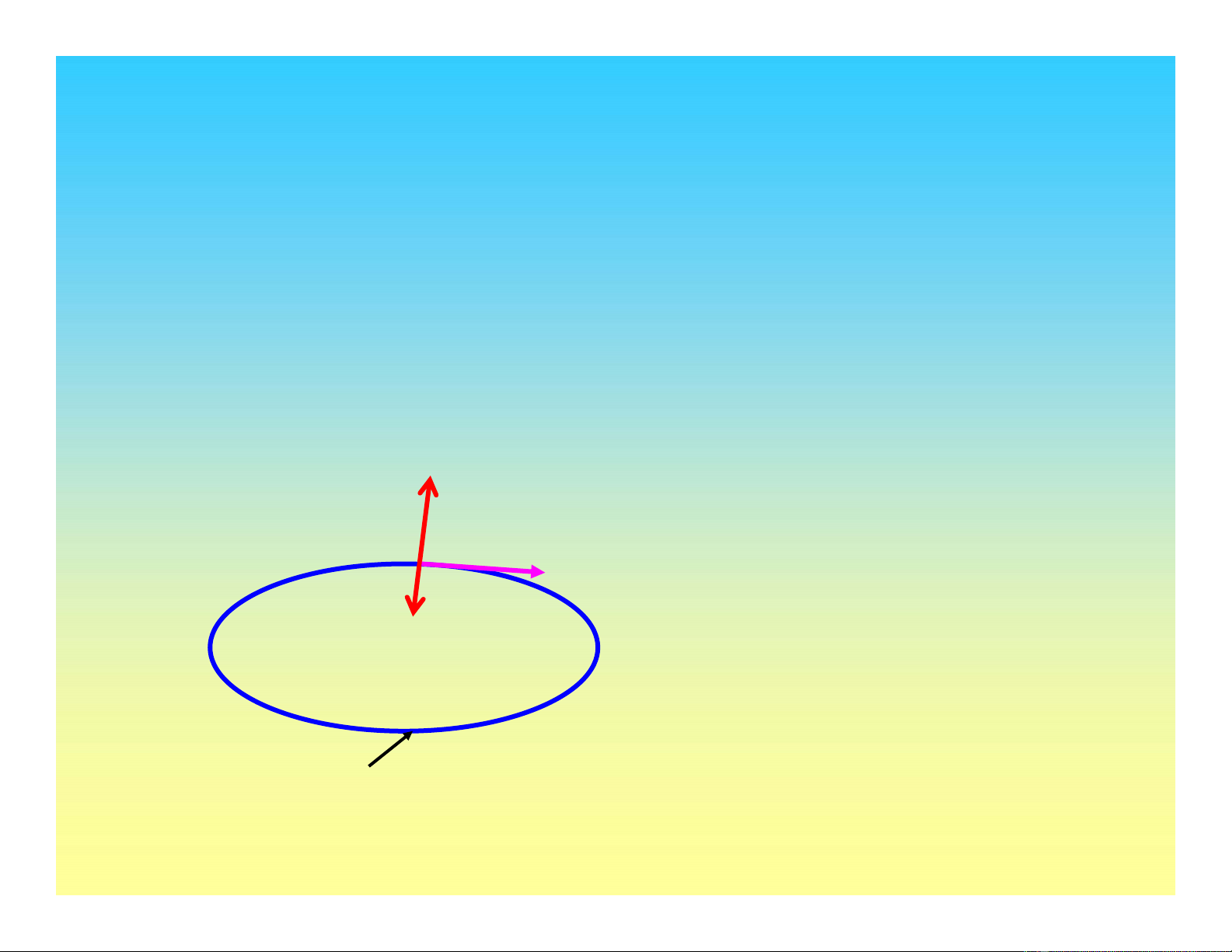
Hàm chảy (Yield function)
•Biến dạng dẻo chỉxảy ra khi một hàm ứng
suất fduy trì lớn nhất và độ tăng df >0
Miền đàn hồi
Miền dẻo
df > 0 : chất tải
df < 0: dỡtải
df = 0: không b/đ tải
Mặt chảy
Chú ý: f, glà hàm độc lập
hệtoạ độÆtham sốlà các
ứng suất chính
Nguyễn Hồng Nam, 2007
28
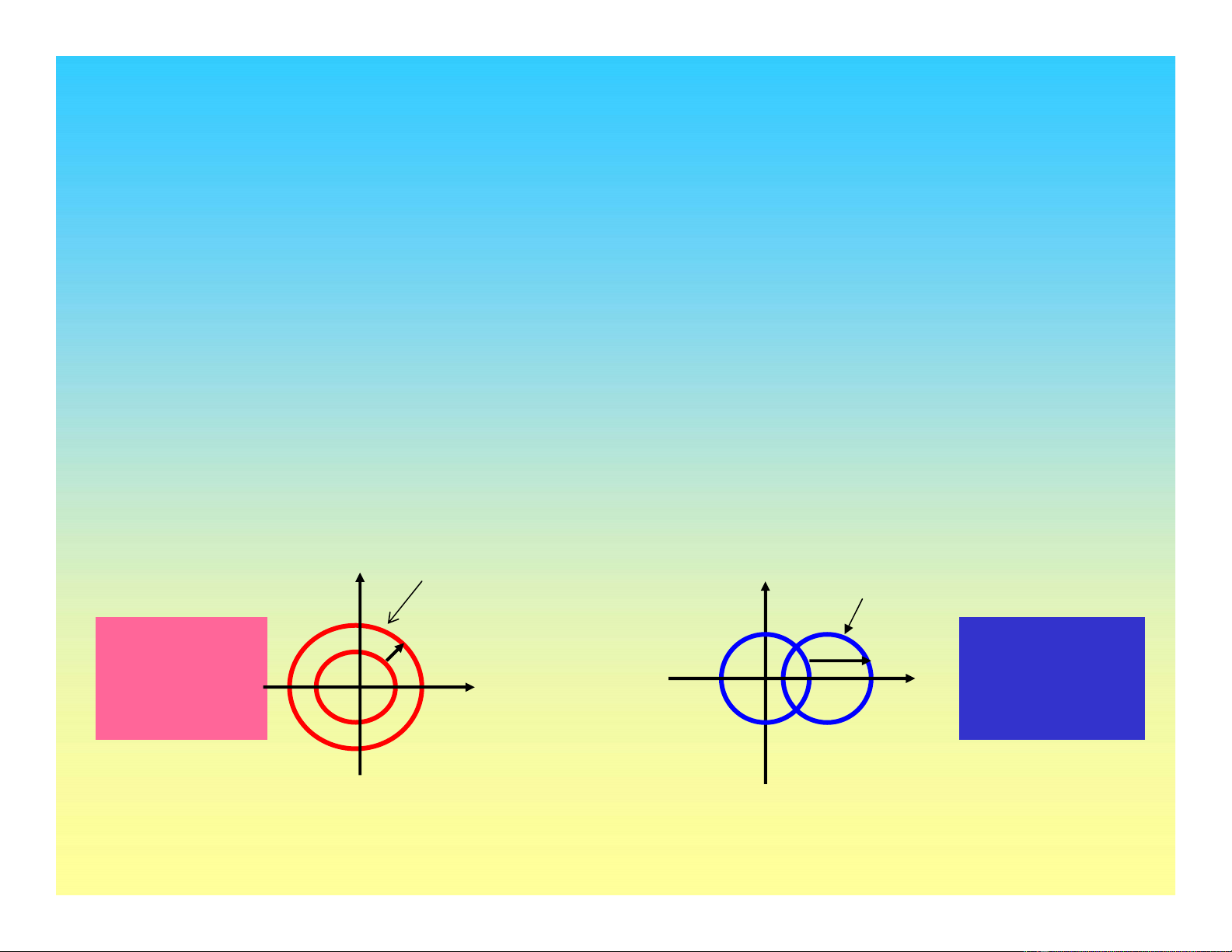
Lý thuyết dẻo
Để mô phỏng các đặc tính biến dạng dẻo, một trong hai giảthiết sau
được sửdụng:
f=g: luật dòng kết hợp (lý thuyết dẻo cổ điển)
f≠g: luật dòng không kết hợp (ứng xửthực của đất)
Ngoài ra, phải có quy luật vềsự thay đổi hàm chảy (Yield function)
Isotropic
hardening
Kinematic
hardening
σj
σi
tăng εp
σi
σj tăng εpi
Nguyễn Hồng Nam, 2007
29
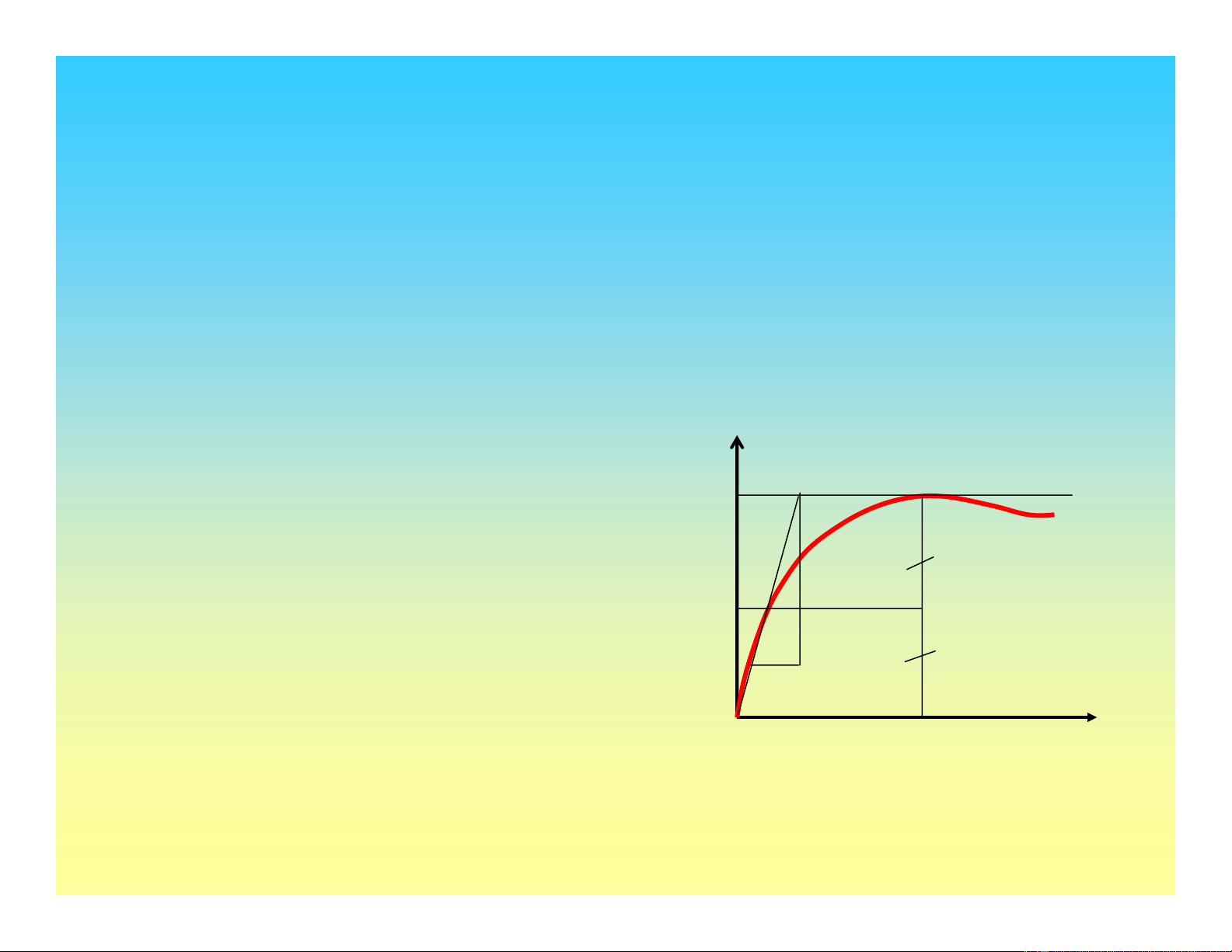
Mô hình đàn hồi tuyến tính tương đương
•Ứng xửthực của đất không
phải đàn hồi, tuyến tính
•Mô đun cát tuyến E50 thường
được sửdụng trong thiết kế sơ
bộ
•E
50 thường được thực hiện từ
thí nghiệm nén nởhông
(unconfined compression test)ε1
q=σ1-σ3
E50
σ3=0
qf
q50
Cách xác định E50 từthí
nghiệm nén nởhông
Nguyễn Hồng Nam, 2007
30
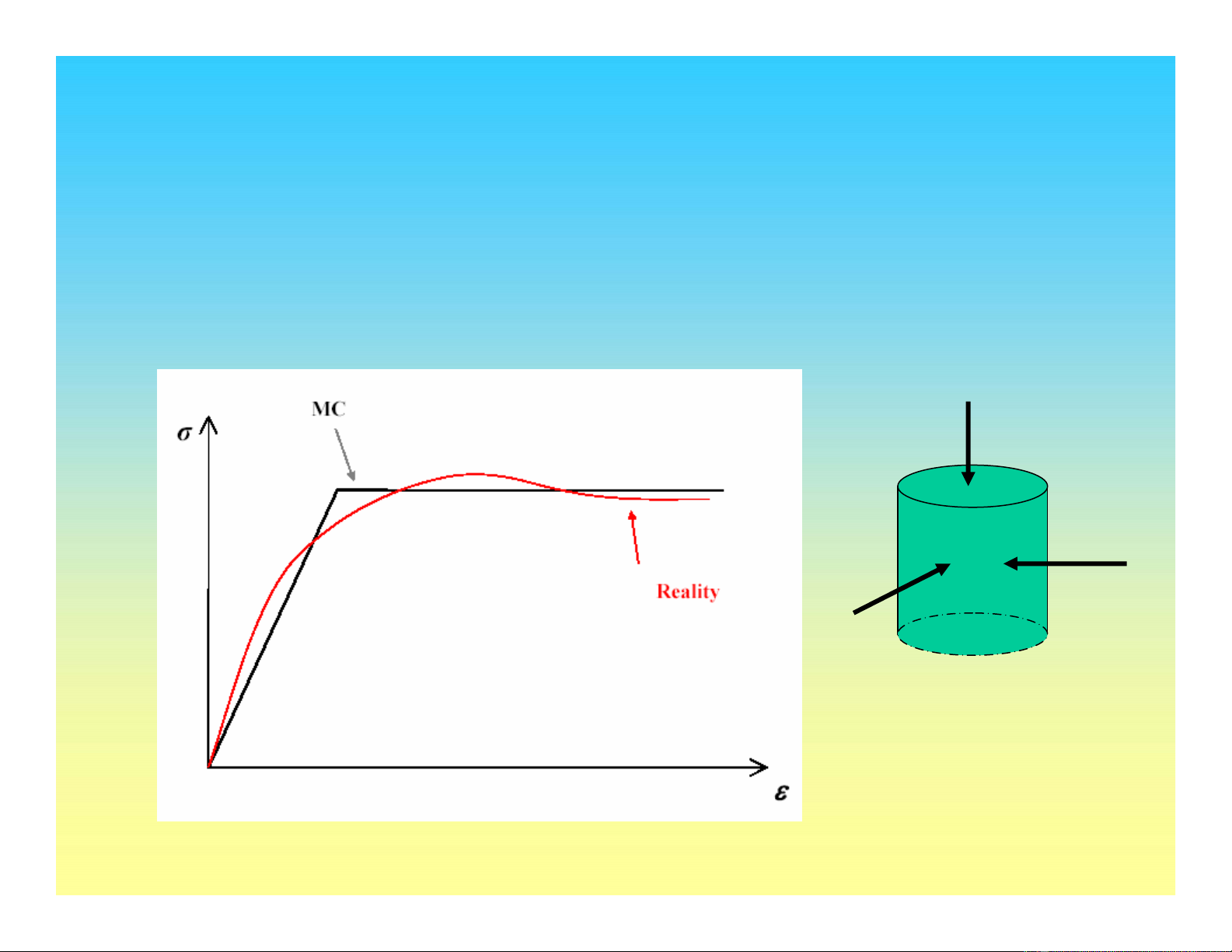
Mô hình Mohr-Coulomb
σy
σx
σz
σx= σz