Luaän vaên toát nghieäp
Nghieân cöùu ñieàu khieån môø – Moâ phoûng heä thoáng ñieàu khieån môø baèng MatLab
21
Ñeå ruùt ngaén thôøi gian tính vaø cuõng ñeå môû roäng coâng thöùc treân cho tröôøng hôïp
ñaàu vaøo laø giaù trò môø, pheùp nhaân ma traän aT.R cuõng ñöôïc thay baèng luaät max-min
cuûa Zadeh nhö ñaõ laøm cho luaät hôïp thaønh MAX-MIN.
Thuaät toaùn xaây döïng R:
Phöông phaùp xaây döïng R cho meänh ñeà hôïp thaønh moät ñieàu kieän R: A
B, theo
MAX-MIN hay MAX-PROD, ñeå xaùc ñònh haøm lieân thuoäc cho giaù trò môø B’ ñaàu ra
hoaøn toaøn coù theå môû roäng töông töï cho moät meänh ñeà hôïp thaønh baát kyø naøo khaùc
daïng:
NEÁU
= A thì
= B,
trong ñoù ma traän hay luaät hôïp thaønh R khoâng nhaát thieát phaûi laø moät ma traän vuoâng.
Soá chieàu cuûa R phuï thuoäc vaøo soá ñieåm laáy maãu cuûa
A(x) vaø
B(y) khi rôøi raïc caùc
haøm lieân thuoäc taäp môø A vaø B.
Chaúng haïn vôùi n ñieåm maãu x1, x2, ..., xn cuûa haøm
A(x) vaø m ñieåm maãu y1, y2, ...,
ym cuûa haøm
B(y) thì luaät hôïp thaønh R laø moät ma traän n haøng m coät nhö sau
nmn
m
mnRnR
mRR
rr
rr
yxyx
yxyx
R
...
......
...
),(...),(
......
),(...),(
1
111
1
111
Haøm lieân thuoäc
B’(y) cuûa giaù trò ñaàu ra öùng vôùi giaù trò roõ ñaàu vaøo xk ñöôïc xaùc
ñònh theo:
B’(y) = aT.R vôùi
aT = (0, 0, ..., 0, 1, 0, ..., 0).
Vò trí thöù k
Trong tröôøng hôïp ñaàu vaøo laø giaù trò môø A’ vôùi haøm lieân thuoäc
A’(x) thì haøm
lieân thuoäc
B’(y) cuûa giaù trò ñaàu ra B’:
B’(y) = (l1, l2, ..., lm)
cuõng ñöôïc tính theo coâng thöùc treân vaø
kii
ni
kral ,minmax
1
, k = 1, 2, ..., m,
trong ñoù a laø vector goàm caùc giaù trò rôøi raïc cuûa caùc haøm lieân thuoäc
A’(x) cuûa A’ taïi
caùc ñieåm
x
X = {x1, x2, ..., xn}, töùc laø
aT = (
A’(x1),
A’(x2), ...,
A’(xn),
Öu ñieåm cuûa luaät max-min Zadeh laø coù theå xaùc ñònh ngay ñöôïc R thoâng qua
tích dyadic, töùc laø tích cuûa moät vector vôùi moät vector chuyeån vò. Vôùi n ñieåm rôøi raïc
Luaän vaên toát nghieäp
Nghieân cöùu ñieàu khieån môø – Moâ phoûng heä thoáng ñieàu khieån môø baèng MatLab
22
x1, x2, ..., xn cuûa cô sôû cuûa A vaø m ñieåm rôøi raïc y1, y2, ..., ym cuûa cô sôû cuûa B thì töø hai
vector:
TA = (
A(x1),
A(x2), ...,
A(xn)) vaø
TB = (
B(y1),
A(y2), ...,
A(ym))
suy ra
R =
TA..
TB,
trong ñoù neáu quy taéc aùp duïng laø MAX-MIN thì pheùp nhaân ñöôïc thay baèng pheùp tính
laáy cöïc tieåu (min), vôùi quy taéc MAX-PROD thì thöïc hieän pheùp nhaân nhö bình
thöôøng.
* Luaät hôïp thaønh cuûa meänh ñeà nhieàu ñieàu kieän:
Moät meänh ñeà hôïp thaønh vôùi d meänh ñeà ñieàu kieän:
NEÁU
1 = A1 VAØ
2 = A2 VAØ ... VAØ
d = Ad thì
= B
bao goàm d bieán ngoân ngöõ ñaàu vaøo
1,
2 , ...,
d vaø moät bieán ñaàu ra
cuõng ñöôïc moâ
hình hoùa gioáng nhö vieäc moâ hình hoùa meänh ñeà hôïp thaønh coù moät ñieàu kieän, trong ñoù
lieân keát VAØ giöõa caùc meänh ñeà (hay giaù trò môø) ñöôïc thöïc hieän baèng pheùp giao caùc
taäp môø A1, A2, ..., Ad vôùi nhau. Keát quaû cuûa pheùp giao seõ laø ñoä thoûa maõn H cuûa luaät.
Caùc böôùc xaây döïng luaät hôïp thaønh R nhö sau:
- Rôøi raïc hoùa mieàn xaùc ñònh haøm lieân thuoäc
A1(x1),
A2(x2), ...,
Ad(xd),
B(y)
cuûa caùc meänh ñeà ñieàu kieän vaø meänh ñeà keát luaän.
- Xaùc ñònh ñoä thoûa maõn H cho töøng vector caùc giaù trò roõ ñaàu vaøo laø vector toå
hôïp d ñieåm maãu thuoäc mieàn xaùc ñònh cuûa caùc haøm lieân thuoäc
Ai(xi), i = 1, ..., d.
Chaúng haïn vôùi moät vector caùc giaù trò roõ ñaàu vaøo
,
trong ñoù ci, i = 1, .., d laø moät trong caùc ñieåm maãu mieàn xaùc ñònh cuûa
Ai(xi) thì
H = MIN{
A1(c1),
A2(c2), ...,
Ad(cd)}
- Laäp R goàm caùc haøm lieân thuoäc giaù trò môø ñaàu ra cho töøng vector caùc giaù trò
ñaàu vaøo theo nguyeân taéc:
B’(y) = MIN{H,
B(y)} neáu quy taéc söû duïng laø MAX-MIN hoaëc
B’(y) = H.
B(y) neáu quy taéc söû duïng laø MAX-PROD.
Luaät hôïp thaønh R vôùi d meänh ñeà ñieàu kieän ñöôïc bieåu dieãn döôùi daïng moät
löôùi khoâng gian (d + 1) chieàu.
Luaän vaên toát nghieäp
Nghieân cöùu ñieàu khieån môø – Moâ phoûng heä thoáng ñieàu khieån môø baèng MatLab
23
* Luaät cuûa nhieàu meänh ñeà hôïp thaønh:
Thuaät toaùn xaây döïng luaät chung cuûa nhieàu meänh ñeà hôïp thaønh
Toång quaùt hoùa phöông phaùp moâ hình hoùa treân cho p meänh ñeà hôïp thaønh:
R1: NEÁU
= A1 thì
= B1, hoaëc
R2: NEÁU
= A2 thì
= B2, hoaëc
...
Rp: NEÁU
= Ap thì
= Bp
trong ñoù caùc giaù trò môø A1, A2, ..., Ap coù cuøng cô sôû X vaø B1, B2, ..., Bp coù cuøng cô sôû Y.
Goïi haøm lieân thuoäc cuûa Ak vaø Bk laø
Ak(x) vaø
Bk(y) vôùi k = 1, 2, ..., p. Thuaät
toaùn trieån khai R = R1
R2
...
Rp seõ nhö sau:
1. rôøi raïc hoùa X taïi n ñieåm x1, x2, ..., xn vaø Y taïi m ñieåm y1, y2, ..., ym,
2. xaùc ñònh caùc vector Ak(x) vaø Bk(y) vôùi k = 1, 2, ..., p theo
TAk = (
Ak(x1),
Ak(x2), ...,
Ak(xn))
TBk = (
Bk(y1),
Ak(y2), ...,
Ak(ym)),
töùc laø Fuzzy hoùa caùc ñieåm rôøi raïc cuûa X vaø Y.
3. Xaùc ñònh moâ hình cho luaät ñieàu khieån
Rk =
TAk.
TBk = (rkij), i = 1, ..., n vaø j = 1, ..., n,
4. Xaùc ñònh luaät hôïp thaønh R = (max{(rkij), k = 1, ..., p}).
Töøng meänh ñeà neân ñöôïc moâ hình hoùa thoáng nhaát theo moät quy taéc chung, ví duï
hoaëc theo quy taéc MAX-MIN hoaëc theo MAX-PROD ... Khi ñoù caùc luaät ñieàu khieån
Rk seõ coù moät teân chung laø luaät hôïp thaønh MAX-MIN hay luaät hôïp thaønh MAX-
PROD. Teân chung naøy seõ laø teân goïi cuûa luaät hôïp thaønh chung R.
4. Giaûi môø:
Boä ñieàu khieån môø cho duø vôùi moät hoaëc nhieàu luaät ñieàu khieån (meänh ñeà hôïp
thaønh) cuõng chöa theå aùp duïng ñöôïc trong ñieàu khieån ñoái töôïng, vì ñaàu ra luoân laø moät
giaù trò môø B’. Moät boä ñieàu khieån môø hoaøn chænh caàn phaûi coù theâm khaâu giaûi môø (quaù
trình roõ hoùa taäp môø ñaàu ra B’).
Giaûi môø laø quaù trình xaùc ñònh moät giaù trò roõ y’ naøo ñoù coù theå chaáp nhaän ñöôïc töø
haøm lieân thuoäc
B’(y) cuûa giaù trò môø B’ (taäp môø). Coù hai phöông phaùp giaûi môø chuû
yeáu laø phöông phaùp cöïc ñaïi vaø phöông phaùp ñieåm troïng taâm, trong ñoù cô sôû cuûa taäp
môø B’ ñöôïc kyù hieäu thoáng nhaát laø Y.
a. Phöông phaùp cöïc ñaïi:
Giaûi môø theo phöông phaùp cöïc ñaïi goàm hai böôùc:
Luaän vaên toát nghieäp
Nghieân cöùu ñieàu khieån môø – Moâ phoûng heä thoáng ñieàu khieån môø baèng MatLab
24
- xaùc ñònh mieàn chöùa giaù trò roõ y’. Giaù trò roõ y’ laø giaù trò maø taïi ñoù haøm lieân
thuoäc ñaït giaù trò cöïc ñaïi (ñoä cao H cuûa taäp môø B’), töùc laø mieàn:
G = {y
Y |
B’(y) = H}.
- xaùc ñònh y’ coù theå chaáp nhaän ñöôïc töø G.
G laø khoaûng [y1, y2] cuûa mieàn giaù trò cuûa taäp môø ñaàu ra B2 cuûa luaät ñieàu khieån
R2: NEÁU
= A2 thì
= B2.
trong soá hai luaät R1, R2 vaø luaät R2 ñöôïc goïi laø luaät quyeát ñònh. Vaäy luaät ñieàu khieån
quyeát ñònh laø luaät Rk, k
{1, 2, ..., p} maø giaù trò môø ñaàu ra cuûa noù coù ñoä cao lôùn nhaát,
töùc laø baèng ñoä cao H cuûa B’.
Ñeå thöïc hieän böôùc hai coù ba nguyeân lyù:
- nguyeân lyù trung bình,
- nguyeân lyù caän traùi vaø
- nguyeân lyù caän phaûi.
Neáu kyù hieäu
)(inf
1yy Gy
vaø )(sup
2yy
Gy
thì y1 chính laø ñieåm caän traùi vaø y2 laø ñieåm caän phaûi cuûa G.
* Nguyeân lyù trung bình:
Theo nguyeân lyù trung bình, giaù trò roõ y’ seõ laø
2
'21 yy
y
Nguyeân lyù naøy thöôøng ñöôïc duøng khi G laø moät mieàn lieân thoâng vaø nhö vaäy y’
cuõng seõ laø giaù trò coù ñoä phuï thuoäc lôùn nhaát. Trong tröôøng hôïp B’ goàm caùc haøm lieân
thuoäc daïng ñeàu thì giaù trò roõ y’ khoâng phuï thuoäc vaøo ñoä thoûa maõn cuûa luaät ñieàu khieån
quyeát ñònh.
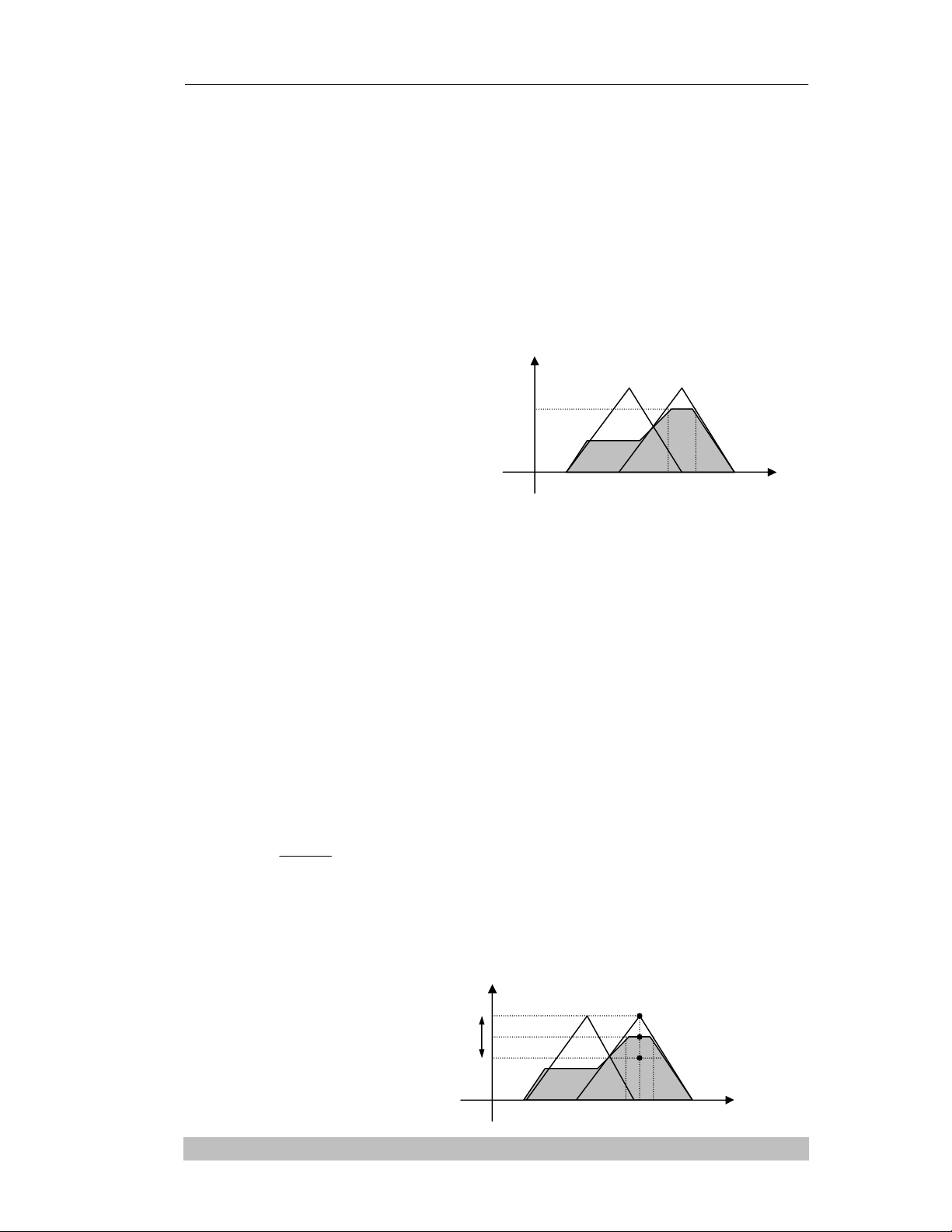
Giaûi môø baèng phöông phaùp cöïc ñaïi.
B
B
1
B
2
y
1
2
H
Giaù trò roõ y’ khoâng phuï
thuoäc vaøo ñaùp öùng vaøo cuûa
luaät ñieàu khieån quyeát ñònh.
y’
B’
B
1
B
2
H
Luaän vaên toát nghieäp
Nghieân cöùu ñieàu khieån môø – Moâ phoûng heä thoáng ñieàu khieån môø baèng MatLab
25
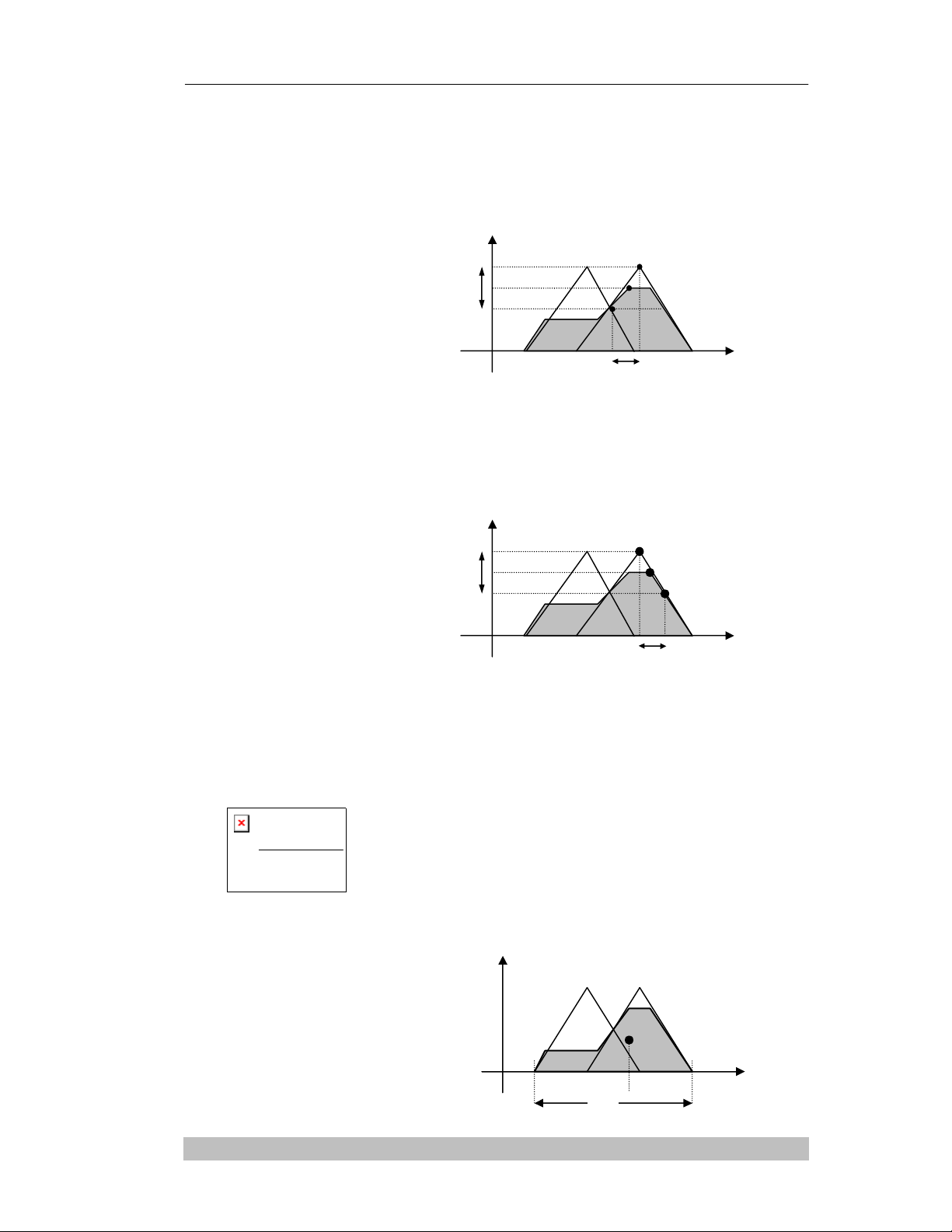
* Nguyeân lyù caän traùi:
Giaù trò roõ y’ ñöôïc laáy baèng caän traùi y1 cuûa G. Giaù trò roõ laáy theo nguyeân lyù caän
traùi naøy seõ phuï thuoäc tuyeán tính vaøo ñoä thoûa maõn cuûa luaät ñieàu khieån quyeát ñònh.
* Nguyeân lyù caän phaûi:
Giaù trò roõ y’ ñöôïc laáy baèng caän phaûi y2 cuûa G. Cuõng gioáng nhö nguyeân lyù caän
traùi, giaù trò roõ y’ ôû ñaây phuï thuoäc tuyeán tính vaøo ñaùp öùng vaøo cuûa luaät ñieàu khieån
quyeát ñònh.
b. Phöông phaùp ñieåm troïng taâm:
Phöông phaùp ñieåm troïng taâm seõ cho ra keát quaû y’ laø hoaønh ñoä cuûa ñieåm troïng
taâm mieàn ñöôïc bao bôûi truïc hoaønh vaø ñöôøng
B’(y).
Coâng thöùc xaùc ñònh y’ theo phöông phaùp ñieåm troïng taâm nhö sau:
S
B
S,
trong ñoù S laø mieàn xaùc ñònh cuûa taäp môø B’.
Giaù trò roõ y’ phuï thuoäc
tuyeán tính vôùi ñaùp öùng vaøo
cuûa luaät ñieàu khieån quyeát
ñònh
y’
B’
B
1
B
2
H
Giaù trò roõ y’ phuï thuoäc
tuyeán tính vôùi ñaùp öùng vaøo
cuûa luaät ñieàu khieån quyeát
ñònh
y’
B’
B
1
B
2
H
Giaù trò roõ y’ laø hoaønh ñoä cuûa
ñieåm troïng taâm.
B
1
B
2
y’
B’
y
S