Luaän vaên toát nghieäp
Nghieân cöùu ñieàu khieån môø – Moâ phoûng heä thoáng ñieàu khieån môø baèng MatLab
31
Trong ñoù:
G(p): haøm truyeàn maïch hôû.
TM: thieát bò coâng ngheä.
R(p), r(t): tín hieäu ñieàu khieån.
C(p), c(t): tín hieäu ra.
N: caùc nhieãu loaïn.
n
i
iii pNpWpRpWpC
1
)()()()()(
)(1
)(
)()( pG
pG
pWpG
Wi(p): haøm truyeàn vôùi caùc nhieãu loaïn.
Giaû söû kích thích ñaàu vaøo laø haøm naác: r(t) = 1(t)
R(p) = 1/p.
p
p
xlp KpGp
pE
1
1
)(1
1
lim
0
Vôùi )(lim
0pGK p
p
: haèng soá sai leäch vò trí
Khi r(t) = t . 1(t)
R(p) = 1/p2:
v
pp
xlv KpGppGp
pE 1
)(.
1
lim
)(1
1
lim 0
2
0
Vôùi )(lim
0ppGK p
v
: haèng soá sai leäch vaän toác.
Khi r(t) = t2/2. 1(t)
R(p) = 1/p3:
a
p
xla KpGp
pE 1
)(1
1
lim 3
0
Vôùi )(lim 2
0pGpK p
a
: haèng soá sai leäch gia toác.
Ñeå taêng ñoä chính xaùc cuûa heä, ngöôøi ta theâm khaâu tích phaân vaøo heä hôû nhöng
khi ñoù ñoä oån ñònh cuûa heä thoáng bò giaûm ñi.
b. Ñoä oån ñònh cuûa heä thoáng:
Vieäc khaûo saùt oån ñònh döïa treân quan ñieåm vaøo chaën ra chaën vôùi caùc tieâu
chuaån: Routh, Hurwitz vaø tieâu chuaån taàn soá Nyquist – Mikhailov cuõng nhö caùc
phöông phaùp chia mieàn D hay quyõ ñaïo nghieäm ñeå khaûo saùt heä coù thoâng soá bieán ñoåi.
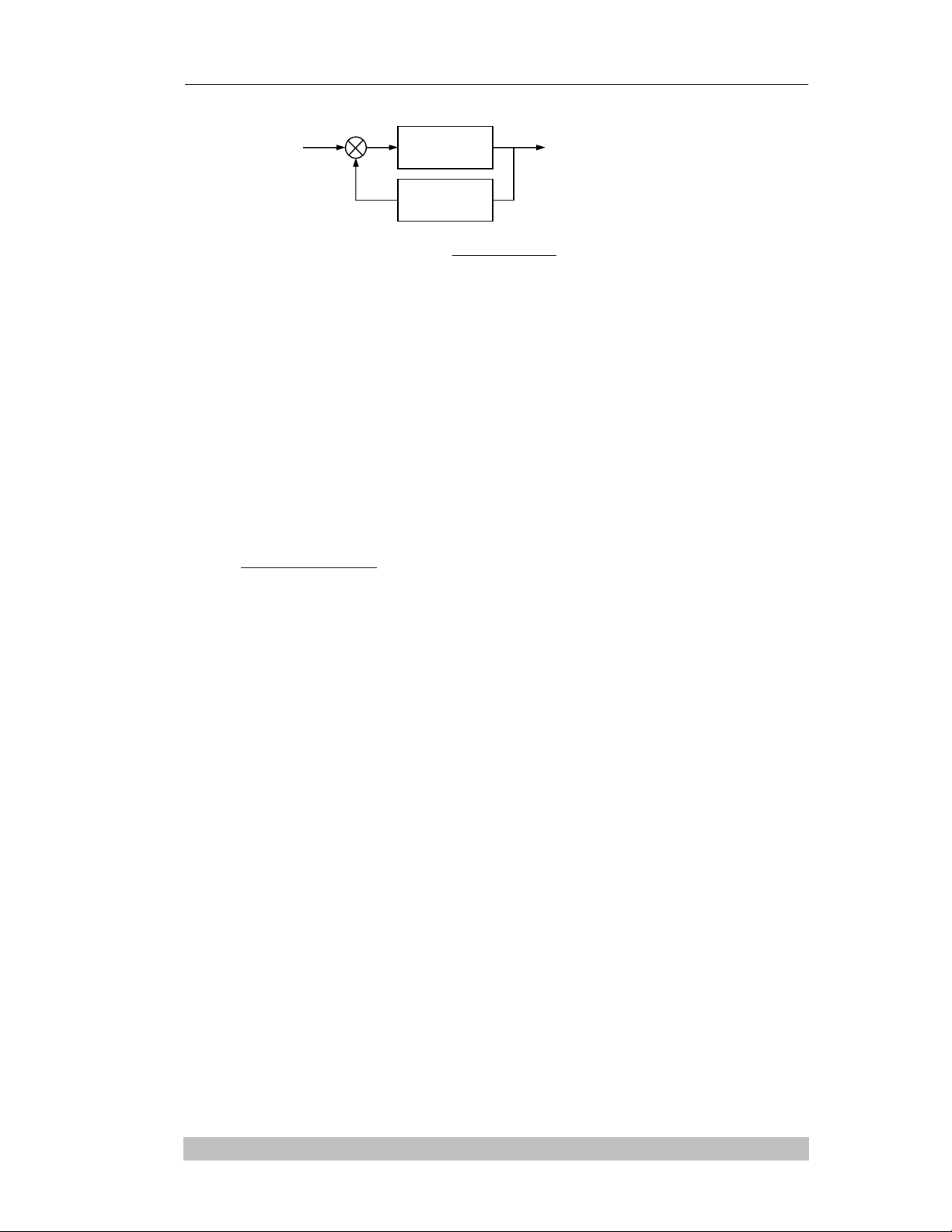
Heä thoáng tuyeán tính ñöôïc goïi laø oån ñònh neáu tín hieäu ra bò chaën khi tín hieäu vaøo
bò chaën. Xeùt moät heä thoáng ñieàu khieån voøng kín cô baûn sau:
Luaän vaên toát nghieäp
Nghieân cöùu ñieàu khieån môø – Moâ phoûng heä thoáng ñieàu khieån môø baèng MatLab
32
Haøm truyeàn voøng kín: )().(1
)(
)( pHpG
pG
pW
Coù phöông trình ñaëc tröng laø: 0)().(1)(
pHpGpF
- Ñieàu khieån caàn vaø ñuû ñeå heä tuyeán tính oån ñònh laø taát caû caùc cöïc Pi cuûa G(p)
phaûi coù phaàn thöïc aâm.
- Re Pi < 0, i hay noùi caùch khaùc nghieäm cuûa phöông trình ñaëc tröng phaûi ôû
beân traùi maët phaúng phöùc.
Ta cuõng goïi heä ôû bieân giôùi oån ñònh khi coù ít nhaát moät nghieäm cuûa phöông trình
ñaëc tröng ôû treân truïc aûo coøn nhöõng nghieäm coøn laïi ôû traùi maët phaúng phöùc.
Heä thoáng seõ khoâng oån ñònh neáu coù ít nhaát moät nghieäm cuûa phöông trình ñaëc
tröng coù phaàn thöïc döông.
* Tieâu chuaån ñaïi soá:
Xeùt moät heä thoáng coù phöông trình ñaëc tröng;
F(p) = anpn + an-1pn-1 + … + a0 = 0, a
0.
Ñieàu kieän caàn ñeå heä oån ñònh laø:
aj cuøng daáu vôùi jan (= 0, 1, …, n)
aj
0 (= 0, 1, …, n).
Tieâu chuaån Hurwitz:
Ñieàu kieän caàn ñeå heä oån ñònh laø caùc nghieäm cuûa phöông trình ñaëc tröng naèm
beân traùi maët phaúng phöùc laø xeùt caû caùc ñònh thöùc Hurwitz Dk (k = 0… n) ñeàu cuøng daáu,
trong ñoù D0 = a, Di = an-1.
Tieâu chuaån Routh:
Ñieàu kieän caàn ñeå caùc nghieäm cuûa phöông trình ñaëc tröng naèm beân traùi maët
phaúng phöùc laø taát caû caùc phaàn töû cuûa coät 1 baûng Routh ñeàu cuøng daáu, neáu coù söï thay
ñoåi daáu thì soá laàn ñoåi daáu baèng soá nghieäm ôû PMP.
Ñoä döï tröõ oån ñònh:
Ñoä döï tröõ oån ñònh laø moät ñaïi löôïng döông ñaùnh giaù möùc ñoä oån ñònh cuûa heä
thoáng vaø neáu vöôït quaù löôïng döï tröõ ñoù thì heä thoáng oån ñònh seõ thaønh maát oån ñònh.
G(p)
H(p)
C(p)
R(p)
Luaän vaên toát nghieäp
Nghieân cöùu ñieàu khieån môø – Moâ phoûng heä thoáng ñieàu khieån môø baèng MatLab
33
* Tieâu chuaån taàn soá:
Tieâu chuaån Nyquist:
Khi G(p) oån ñònh thì heä kín oån ñònh khi vaø chæ khi bieåu ñoà Nyquist bao ñieåm -1.
Khi G(p) khoâng oån ñònh thì heä kín oån ñònh khi vaø chæ khi bieåu ñoà Nyquist bao ñieåm –
1 m laàn.
Tieâu chuaån giaûn ñoà Bode:
Heä oån ñònh khi G(p) khoâng ñöôïc coù cöïc ôû phaàn maët phaúng phöùc.
Xeùt ñaëc tính pha ôû taàn soá caét bieân WB, xem ñaëc tính pha ôû taàn soá caét bieân neáu:
- Ñöôøng pha ôû treân ñöôøng –180o thì heä kín oån ñònh.
- Ñöôøng pha ôû ñöôøng –180o thì heä kín ôû bieân giôùi oån ñònh.
- Ñöôøng pha ôû döôùi ñöôøng –180o thì heä kín khoâng oån ñònh.
4. Caùc kieåu ñieàu khieån coå ñieån:
a. Ñieàu khieån tæ leä P:
Ñieàu khieån tæ leä cho pheùp nhanh choùng ñaït trò soá yeâu caàu nhöng thöôøng coù sai
leäch. Ñeå giaûm sai leäch ngöôøi ta taêng ñoä lôïi K, neáu taêng K quaù daãn ñeán voït loá
max lôùn
vaø heä coù theå maát oån ñònh.
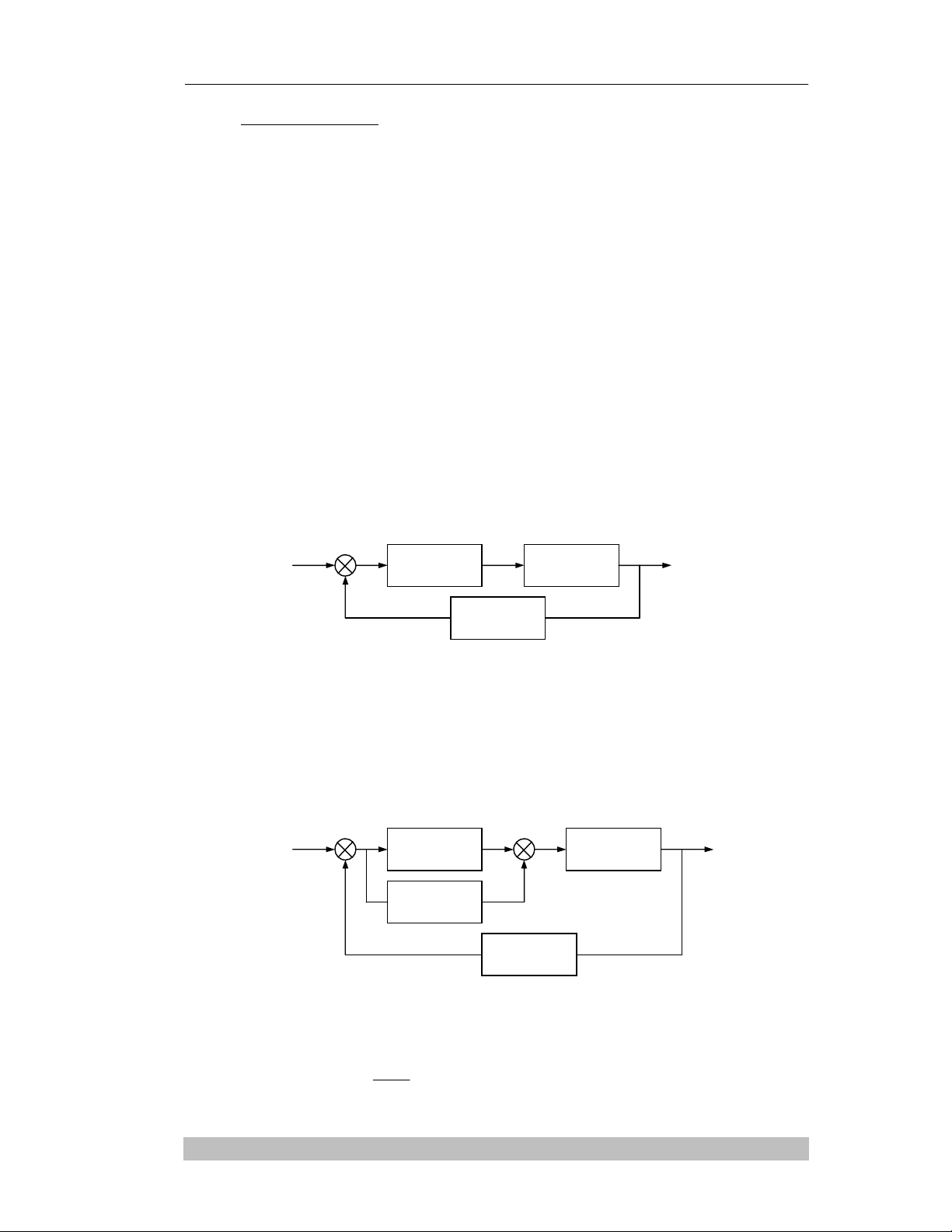
b. Ñieàu khieån tæ leä – vi phaân PD:
Trong heä thoáng maø ñoä voït loá quaù lôùn thì ngöôøi ta thöôøng theâm khaâu ñieàu khieån
vi phaân:
dt
tde
TtKetU d
)(
)()(
K
u(t)
G(p)
H(p)
C(t)
r(t)
e(t)
f(t)
-
K
u(t)
G(p)
T
d
p
C(t)
r(t)
e(t)
H(p)
+
+
Luaän vaên toát nghieäp
Nghieân cöùu ñieàu khieån môø – Moâ phoûng heä thoáng ñieàu khieån môø baèng MatLab
34
Neáu C(t) taêng (ñoä voït loá lôùn) thì e(t) giaûm 0
)(
dt
tde , neân
dt
tde
TtKetU d
)(
)()( giaûm nhieàu khoâng cho C(t) taêng quaù. Vì vaäy ñieàu khieån PD
laøm giaûm chaán cuûa heä thoáng taêng leân, giaûm voït loá nhöng thôøi gian treã seõ laâu hôn.
Ñieàu khieån PD chæ aûnh höôûng tôùi sai soá xaùc laäp Exl, neáu Exl bieán thieân theo thôøi
gian ( 0
dt
d) maø khoâng aûnh höôûng neáu Exl(t) = Cte. Neáu Exl taêng theo t, tín hieäu taùc
ñoäng coù thaønh phaàn tæ leä vôùi dt
tde )( laøm giaûm bieân ñoä sai soá.
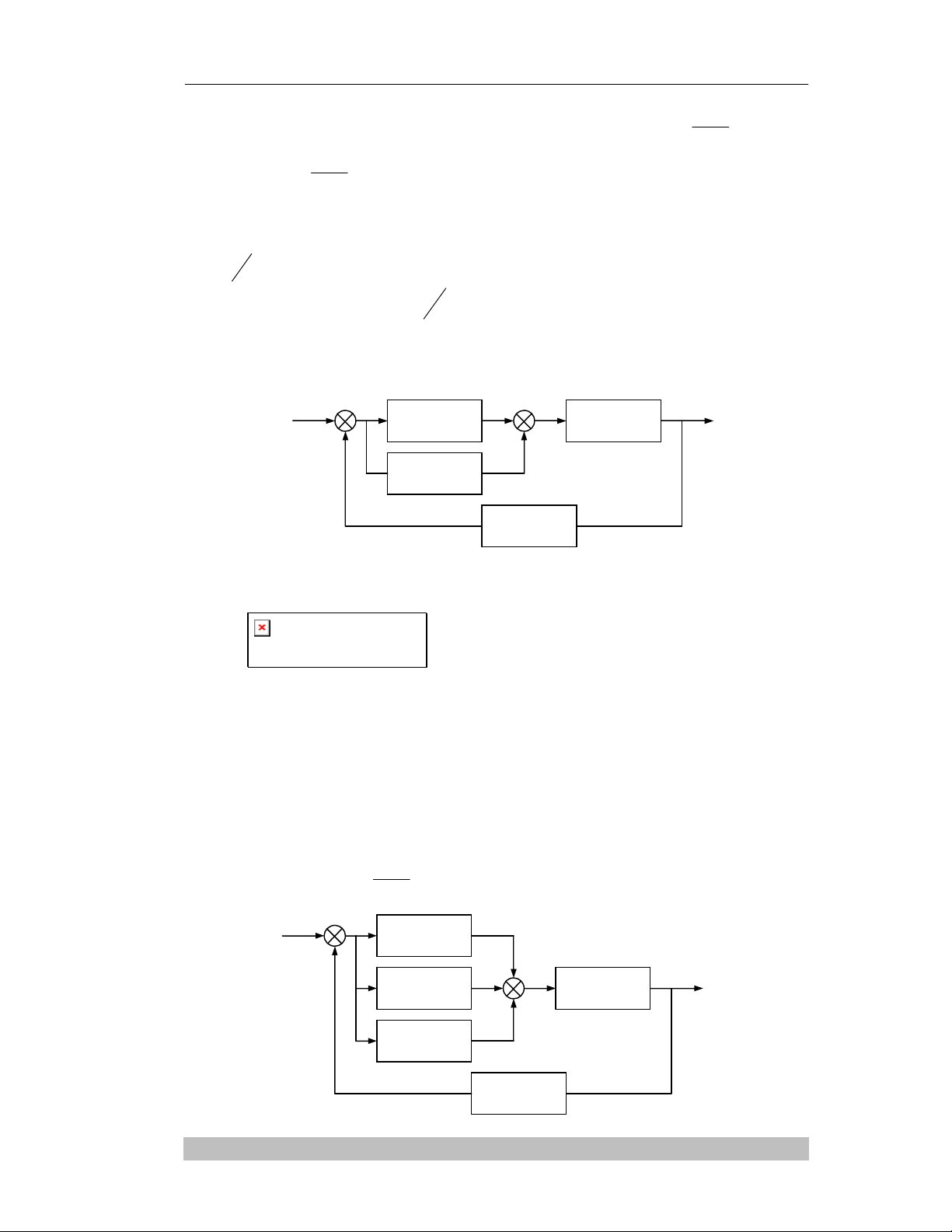
c. Ñieàu khieån tæ leä – tích phaân PI:
Ñeå naâng cao ñoä chính xaùc cuûa heä thoáng, ngöôøi ta theâm khaâu ñieàu khieån tích
phaân. Tín hieäu taùc ñoäng:
t
idtteK
e
Bao laâu coøn sai leäch, tín hieäu taùc ñoäng coøn duy trì ñeå laøm giaûm sai leäch naøy.
Ñieàu khieån PI laøm cho heä höõu sai thaønh voâ sai. Loaïi cuûa heä thoáng ñöôïc taêng leân
nghóa laø baäc cuûa noù cuõng taêng leân, do ñoù ñoä oån ñònh cuûa heä keùm ñi.
d. Ñieàu khieån tæ leä – tích phaân – vi phaân PID:
Ñeå caûi thieän heä thoáng ôû xaùc laäp vaø quaù ñoä thì tín hieäu taùc ñoäng:
t
id dtteK
dt
tde
TtKetU
0
)(
)(
)()(
-
K
u(t)
G(p)
K
i
p
C(t)
r(t)
e(t)
H(p)
+
+
-
K
u(t)
G(p)
T
d
p
C(t)
r(t)
e(t)
H(p)
+
+
K
i
p
+
Luaän vaên toát nghieäp
Nghieân cöùu ñieàu khieån môø – Moâ phoûng heä thoáng ñieàu khieån môø baèng MatLab
35
5. Boä ñieàu khieån môø:
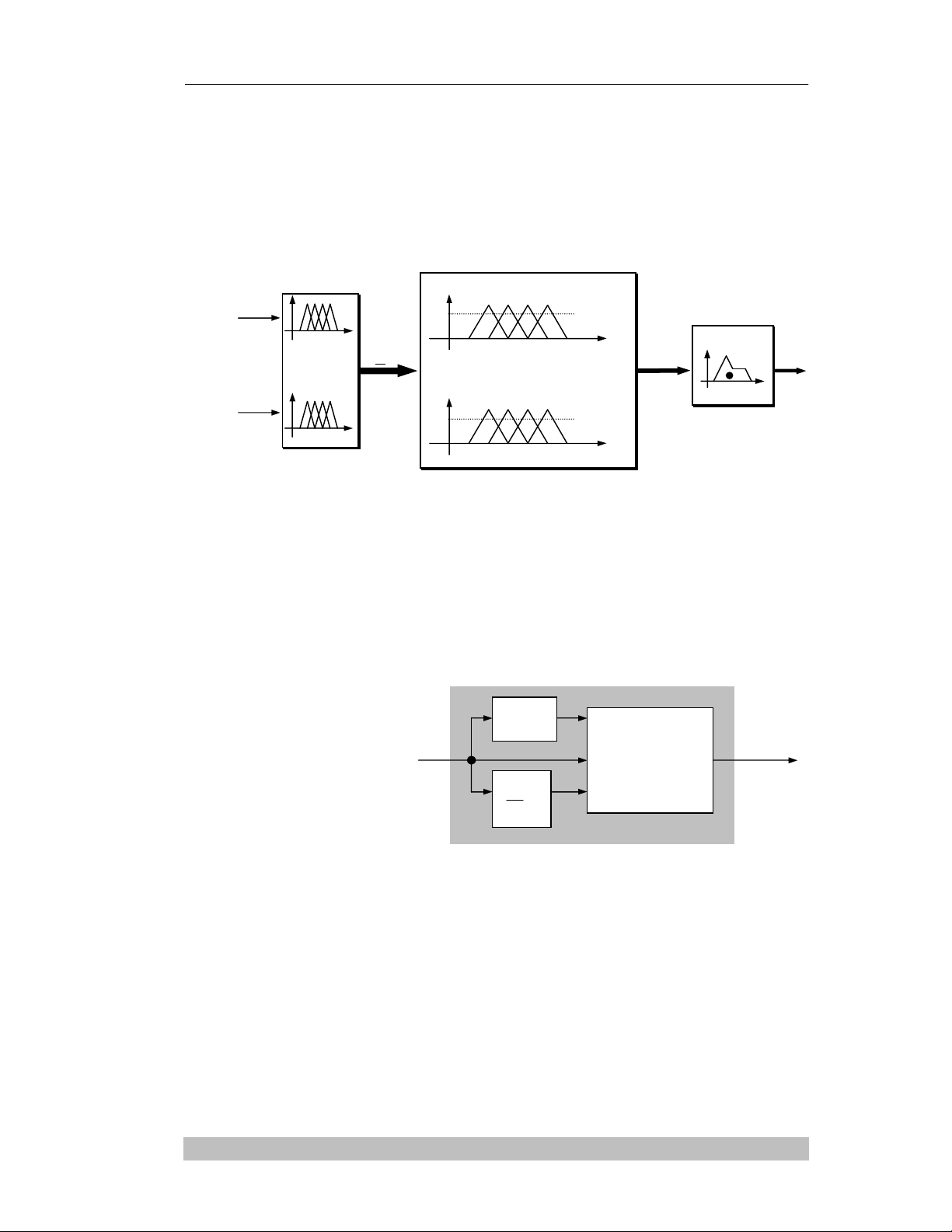
a. Boä ñieàu khieån môø cô baûn:
Nhöõng thaønh phaàn cô baûn cuûa moät boä ñieàu khieån môø bao goàm khaâu Fuzzy hoùa,
thieát bò thöïc hieän luaät hôïp thaønh vaø khaâu giaûi môø. Moät boä ñieàu khieån môø chæ goàm ba
thaønh phaàn nhö vaäy coù teân goïi laø boä ñieàu khieån môø cô baûn.
Do boä ñieàu khieån môø cô baûn chæ coù khaû naêng xöû lyù caùc giaù trò tín hieäu hieän thôøi
neân noù thuoäc nhoùm caùc boä ñieàu khieån tónh. Tuy vaäy ñeå môû roäng mieàn öùng duïng cuûa
chuùng vaøo caùc baøi toaùn ñieàu khieån ñoäng, caùc khaâu ñoäng hoïc caàn thieát seõ ñöôïc noái
theâm vaøo boä ñieàu khieån môø cô baûn. Caùc khaâu ñoäng ñoù chæ coù nhieäm vuï cung caáp
theâm cho boä ñieàu khieån môø cô baûn caùc giaù trò ñaïo haøm hay tích phaân cuûa tín hieäu.
Vôùi nhöõng khaâu ñoäng boå sung naøy, boä ñieàu khieån cô baûn seõ ñöôïc goïi laø boä ñieàu
khieån môø ñoäng.
b. Toång hôïp boä ñieàu khieån môø:
* Ñònh nghóa caùc bieán vaøo ra:
Xaùc ñònh caùc bieán ngoân ngöõ vaøo/ra vaø ñaët teân cho chuùng.
* Xaùc ñònh taäp môø:
Ñònh nghóa caùc bieán ngoân ngöõ vaøo/ra bao goàm soá caùc taäp môø vaø daïng caùc haøm
lieân thuoäc cuûa chuùng, caàn xaùc ñònh:
Mieàn giaù trò vaät lyù (cô sôû) cuûa caùc bieán ngoân ngöõ vaøo/ra
Soá löôïng taäp môø (giaù trò ngoân ngöõ)
x
1
x
q
...
...
R
1
: NEÁU ... THÌ ...
R
q
: NEÁU ... THÌ ...
...
H
1
H
q
B’
y’
Boä ñieàu khieån môø cô baûn.
Boä ñieàu
khieån môø cô
baûn
...
dt
d
dt...
x(t)
y’(t)
Boä ñieàu khieån môø ñoäng.