
Robot c«ng nghiÖp 84
ch−¬ng VII
§éng lùc häc Robot
(Dynamic of Robot)
7.1. NhiÖm vô vµ ph−¬ng ph¸p ph©n tÝch ®éng lùc häc robot
Nghiªn cøu ®éng lùc häc robot lµ c«ng viÖc cÇn thiÕt khi ph©n tÝch còng nh− tæng
hîp qu¸ tr×nh ®iÒu khiÓn chuyÓn ®éng. ViÖc nghiªn cøu ®éng lùc häc robot th−êng gi¶i
quyÕt hai nhiÖm vô sau ®©y :
1/ X¸c ®Þnh momen vµ lùc ®éng xuÊt hiÖn trong qu¸ tr×nh chuyÓn ®éng. Khi ®ã qui
luËt biÕn ®æi cña biÕn khíp qi(t) coi nh− ®· biÕt.
ViÖc tÝnh to¸n lùc trong c¬ cÊu tay m¸y lµ rÊt cÇn thiÕt ®Ó chän c«ng suÊt ®éng c¬,
kiÓm tra ®é bÒn, ®é cøng v÷ng, ®¶m b¶o ®é tin cËy cña robot.
2/ X¸c ®Þnh c¸c sai sè ®éng tøc lµ sai lÖch so víi qui luËt chuyÓn ®éng theo ch−¬ng
tr×nh. Lóc nÇy cÇn kh¶o s¸t Ph−¬ng tr×nh chuyÓn ®éng cña robot cã tÝnh ®Õn ®Æc tÝnh ®éng
lùc cña ®éng c¬ vµ c¸c kh©u.
Cã nhiÒu ph−¬ng ph¸p nghiªn cøu ®éng lùc häc robot, nh−ng th−êng gÆp h¬n c¶ lµ
ph−¬ng ph¸p c¬ häc Lagrange, cô thÓ lµ dïng ph−¬ng tr×nh Lagrange - Euler. §èi víi c¸c
kh©u khíp cña robot, víi c¸c nguån ®éng lùc vµ kªnh ®iÒu khiÓn riªng biÖt, kh«ng thÓ bá
qua c¸c hiÖu øng träng tr−êng (gravity effect), qu¸n tÝnh (initial), t−¬ng hæ (Coriolis), ly
t©m (centripetal)... mµ nh÷ng khÝa c¹nh nÇy ch−a ®−îc xÐt ®Çy ®ñ trong c¬ häc cæ ®iÓn; C¬
häc Lagrange nghiªn cøu c¸c vÊn ®Ò nªu trªn nh− mét hÖ thèng khÐp kÝn nªn ®©y lµ nguyªn
lý c¬ häc thÝch hîp ®èi víi c¸c bµi to¸n ®éng lùc häc robot.
7.2. C¬ häc Lagrange víi c¸c vÊn ®Ò ®éng lùc cña robot.
Hµm Lagrange cña mét hÖ thèng n¨ng l−îng ®−îc ®Þnh nghÜa :
L = K - P (7.1)
Trong ®ã : K lµ tæng ®éng n¨ng cña hÖ thèng
P lµ tæng thÕ n¨ng
K vµ P ®Òu lµ nh÷ng ®¹i l−îng v« h−íng nªn cã thÓ chän bÊt cø hÖ to¹ ®é thÝch hîp
nµo ®Ó bµi to¸n ®−îc ®¬n gi¶n. §èi víi mét robot cã n kh©u, ta cã :
vµ
KK
i
i
n
=∑
=1PP
i
i
n
=∑
=1
ë ®©y, Ki vµ Pi lµ ®éng n¨ng vµ thÕ n¨ng cña kh©u thø i xÐt trong hÖ to¹ ®é chän.Ta
biÕt mçi ®¹i l−îng Ki vµ Pi lµ mét hµm sè phô thuéc nhiÒu biÕn sè:
K
i = K(qi, ) vµ P
i
q
&i = P(qi, )
&
qi
Víi qi lµ to¹ ®é suy réng cña khíp thø i. NÕu khíp thø i lµ khíp quay th× qi lµ gãc
quay θi, nÕu lµ khíp tÞnh tiÕn th× qi lµ ®é dµi tÞnh tiÕn di.
Ta ®Þnh nghÜa : Lùc t¸c dông lªn kh©u thø i (i=1, 2,..., n) víi quan niÖm lµ lùc tæng
qu¸t (Generalized forces), nã cã thÓ lµ mét lùc hoÆc mét momen (phô thuéc vµo biÕn khíp
qi lµ tÞnh tiÕn hoÆc quay), ®−îc x¸c ®Þnh bëi:
Fi=−
d
dt
L
q
L
q
ii
∂
∂
∂
∂
& (7.2)
TS. Ph¹m §¨ng Ph−íc
Robot c«ng nghiÖp 85
Ph−¬ng tr×nh nÇy ®−îc gäi lµ ph−¬ng tr×nh Lagrange-Euler, hay th−êng ®−îc gäi t¾t
lµ ph−¬ng tr×nh Lagrange.
7.3. VÝ dô ¸p dông :
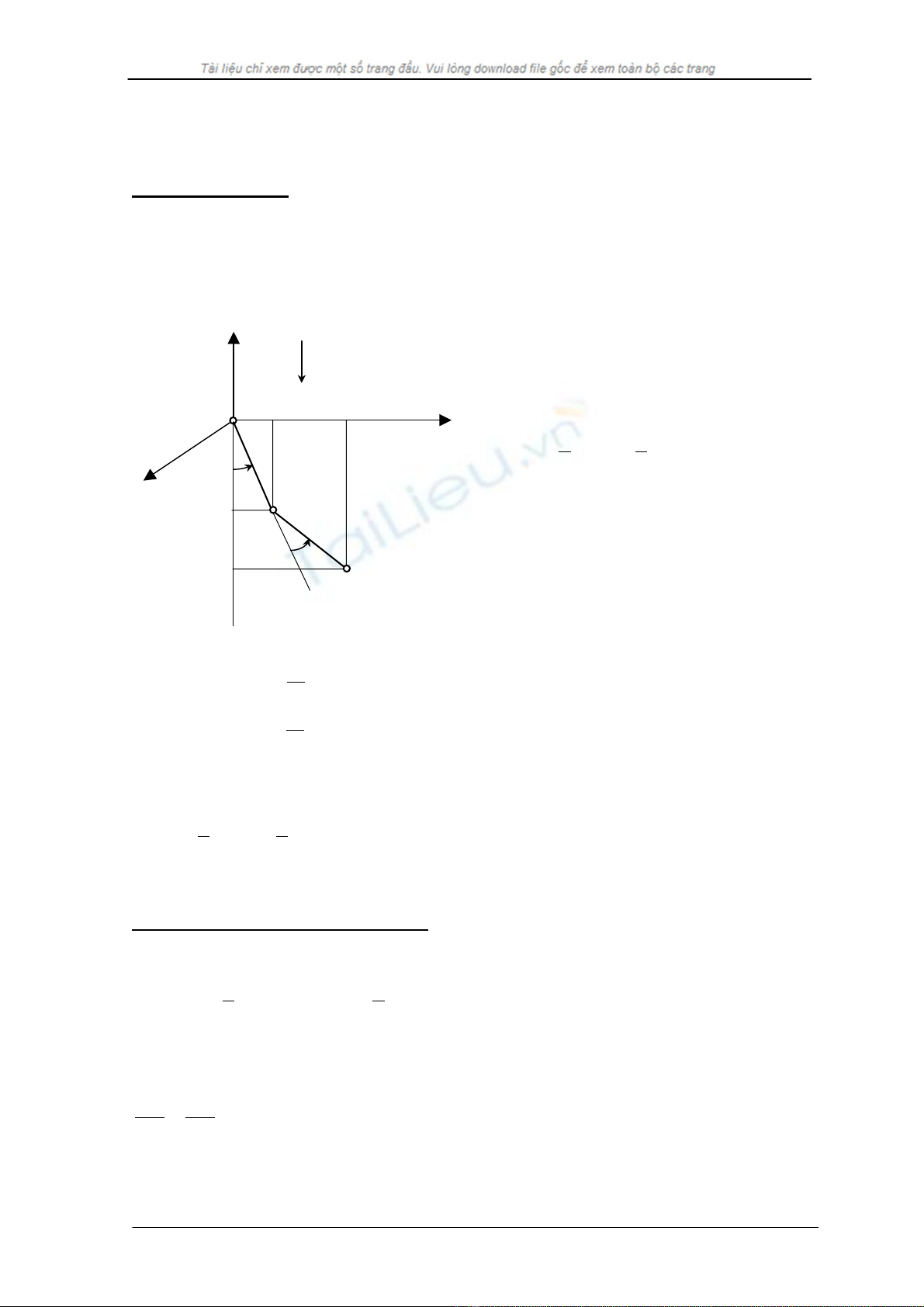
XÐt mét robot cã hai kh©u nh− h×nh vÏ, C¸c kh©u cã chiÒu dµi lµ d1 vµ d2 víi c¸c
khèi l−îng t−¬ng øng m1 vµ m2 qui ®æi vÒ ®Çu mót cña kh©u. Robot ®−îc ®Æt th¼ng ®øng
chÞu gia tèc träng tr−êng g. C¸c khíp chuyÓn ®éng quay víi c¸c biÕn khíp θ1 vµ θ2. TÝnh
lùc tæng qu¸t.
Qua vÝ dô nÇy, chØ víi mét mèi liªn kÕt hai
kh©u, c¸c vÊn ®Ò ®Æt ra ®Òu ®· cã mÆt
trong qu¸ tr×nh nghiªn cøu ®éng lùc häc,
vµ do ®ã, vÝ dô nªu trªn cã thÓ më réng ®Ó
¸p dông trong nh÷ng tr−êng hîp phøc t¹p
h¬n. §èi víi kh©u 1 :
m2
m1
θ2
θ1
g = 9,81m/s2
y2
y1
x2
x1
O0
z
x
y
Kmvmd
111
211
21
2
1
2
1
2
==
&
θ (7.3)
P1 = -m1gd1cosθ1 (7.4)
§èi víi kh©u 2 :
VÒ to¹ ®é :
x
2 = d1sinθ1 + d2sin(θ1 + θ2)
y
2 = -d1cosθ1 - d2cos(θ1 + θ2)
ChiÒu cao thÕ n¨ng :
h = d1cosθ1 + d2cos(θ1 + θ2)
VÒ mÆt vËn tèc : vxy
2
22
22
2
=+
&&
Víi &cos( )&cos( )(&&
)x d
dt xd d
2 2 1 112 1212
== + + +θθ θ θ θ θ
&sin( )&sin( )(&&
)y d
dt yd d
221112121
== + + +θθ θθθθ
2
[
]
vd d dd
2
21
21
22
21
212 2
212 2 1
212
22=++++ +
&(&&&&
)cos()(
&&&
)θθθθθ θθθθ
§éng n¨ng vµ thÕ n¨ng sÏ lµ :
[]
Kmvmdd dd
222
221
21
22
21
212 2
212 2 1
212
1
2
1
222== ++++ +
&(&&&&
)cos()(
&&&
)θθθθθ θθθθ (7.5)
(7.6)
[]
Pmgd d
221121
=− + +cos( ) cos( )θθ
2
θ
7.4. Hµm Lagrange vµ lùc tæng qu¸t :
¸p dông hµm Lagrange cho vÝ dô trªn, ta cã :
L = (K
1 + K2) - (P1 + P2)
L m m d md mdd=+ + +++ +
1
2
1
22
121
21
222
21
212 2
2212 2 1
212
()
&(&&&&
)cos(
&&&
)θθθθθ θθθ+θ
++
+
+
()cos cos(mmgd mgd
121 122 12
)
θ
θ
θ
(7.7)
Khi tÝnh lùc tæng qu¸t, c¸c biÕn cña hÖ : q1 = θ1 vµ q2 = θ2.
§èi víi kh©u 1 :
∂
∂
∂
∂θ θθθ θθ θ
L
q
Lmmd md mdd mdd
&&()
&(&&
)cos
&cos &
11121
2122
212 212 21 212 2
2==+ + ++ + θ
2
TS. Ph¹m §¨ng Ph−íc

Robot c«ng nghiÖp 86
d
dt
Lmmd md mdd mdd
∂
∂θ θθθ θθθ θ
&()
&& (&& && )sin
&& cos &&
1121
2122
21 2 212 221 212 21
22=+ + +− + θ
−
−+ mdd mdd
212 22
2212 22
sin &cos &&
θθ θθ
∂
∂
∂
∂θ θθ
L
q
Lmmgd mgd
11 121 122 12
==−+ − +()sin sin(
θ
)
VËy :
Fd
dt
LLmmd md mdd
md mdd mdd mdd
mmgd mgd
111121
222
2212 2 1
22
2212 2 2 212 221 212 22
2
121122 12
2
2
=−=+++ +
++ − −
++ + +
∂
∂θ
∂
∂θ θθ
θ θ θθθ θθ
θθθ
&[( ) cos ]&&
[cos]
&& sin && sin &
()sin sin()
+
(7.8)
Muèn cho kh©u 1 quay ®−îc mét gãc θ1 th× ®éng c¬ ph¶i t¹o ra mét lùc tæng qu¸t ≥
F1. Lùc tæng qu¸t nÇy cã ®Æc tÝnh phi tuyÕn, lµ hîp t¸c dông cña nhiÒu yÕu tè (non linear
and cuppling).
T−¬ng tù, ®Ó tÝnh lùc tæng qu¸t cña kh©u thø hai , ta cã :
∂
∂θ θθ θ
Lmd md mdd
&
&& cos &
222
2122
22212 2
=++ θ
1
d
dt
Lmd md mdd mdd
∂
∂θ θθ θθ θθ
&
&& && cos && sin &&
222
2122
22212 21212 21
=++ − θ
2
vµ )sin()sin()sin( 2122
2
12212212212
2
θθθθθθθ
∂θ
∂
+−−−−= gdmddmddm
L&&&
VËy :
)sin()sin(
]cos[
2122
2
12212
2
2
2212212
2
22
22
2
θθθθ
θθθ
∂θ
∂
θ∂
∂
++−
++=−=
gdmddm
dmddmdm
LL
dt
d
F
&
&&&&
& (7.9)
§Ó ph©n tÝch ý nghÜa c¸c thµnh phÇn trong biÓu thøc tÝnh lùc tæng qu¸t, ta viÕt l¹i
c¸c biÓu thøc F1, F2 nh− sau :
FD D D D D D D
1 11 1 12 2 111 1
2122 2
2112 1 2 121 1 2 1
=++ + + + +
&& && & & & & & &
θ θ θ θ θθ θθ
FD D D D D D D
2 12 1 22 2 211 1
2222 2
2212 1 2 221 1 2 2
=++ + + + +
&& && & & && &&
θθθθθθθθ
HiÖu øng HiÖu øng HiÖu øng HiÖu øng
qu¸n tÝnh ly t©m t−¬ng hæ träng tr−êng
Effective inertias Centripetal effect Coriolis effect Gravity
(Trong ®ã : D111 = 0; D222 = 0; D112 = D121 = D212 = D221 =-m2d1d2sinθ2 ...)
Trong c¸c biÓu thøc trªn, c¸c hÖ sè d¹ng Dii hoÆc thÓ hiÖn hiÖu øng qu¸n tÝnh t¹i
khíp i hoÆc j g©y ra bëi gia tèc t¹i khíp i hoÆc j. C¸c sè h¹ng cã d¹ng
ij
D
2
ijj
Dj
θ
&lµ lùc ly t©m
t¸c ®éng lªn khíp i g©y ra bëi vËn tèc t¹i khíp j. Sè h¹ng d¹ng lµ lùc
Cariolis t¸c ®éng lªn khíp thø i g©y ra do vËn tèc t¹i khíp j vµ k. Sè h¹ng cã d¹ng D
jkkj
θθθθ
&&&& ikjijk DD +
i lµ lùc
träng tr−êng t¸c ®éng lªn khíp i.
TS. Ph¹m §¨ng Ph−íc
Robot c«ng nghiÖp 87
7.5. Ph−¬ng tr×nh ®éng lùc häc robot :
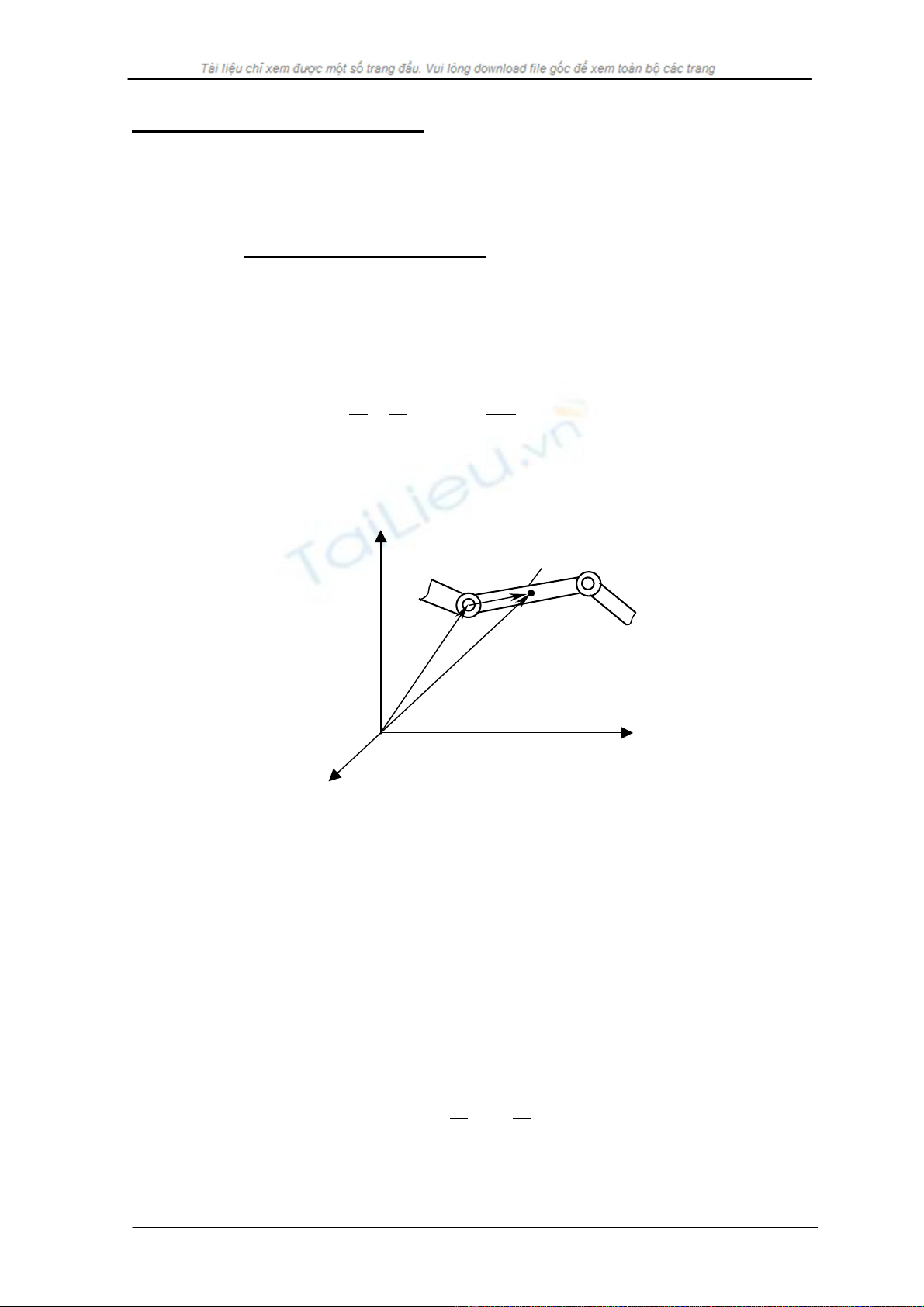
XÐt kh©u thø i cña mét robot cã n kh©u. TÝnh lùc tæng qu¸t Fi cña kh©u thø i víi
khèi l−îng vi ph©n cña nã lµ dm. Lùc tæng qu¸t Fi ®ãng vai trß rÊt quan träng khi x©y dùng
s¬ ®å khèi ®Ó thiÕt lËp hµm ®iÒu khiÓn cho robot cã n bËc tù do.
7. 5. 1. VËn tèc cña mét ®iÓm trªn robot :
Mét ®iÓm trªn kh©u thø i ®−îc m« t¶ trong hÖ to¹ ®é c¬ b¶n lµ :
r = T
i. ir (7.10)
Trong ®ã : ir lµ to¹ ®é cña ®iÓm xÐt ®èi víi kh©u thø i, ir kh«ng thay ®æi theo thêi
gian. Ti lµ ma trËn chuyÓn ®æi tõ kh©u thø i vÒ hÖ to¹ ®é gèc : Ti = A1A2...Ai. Nh− vËy r lµ
mét hµm cña thêi gian t.
Tèc ®é cña vi khèi l−îng dm ®−îc tÝnh bëi c«ng thøc :
&
rdr
dt
d
dt Tr T
qq
iii
j
j
i
ji
== =
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
=
∑∂
∂
1
&
r (7.11)
Khi tÝnh b×nh ph−¬ng cña vËn tèc nÇy ta cã :
(7.12)
&.&(&,&,&)(
&& )rr rxyz Trrr
ooo T
==
∑2
z
x
y
i rdm
Kh©u i
O0
Ti
r
H×nh 7.1. Kh¶o s¸t tèc ®é cña vi khèi l−îng dm.
Víi rT lµ chuyÓn vÞ vect¬ vµ Tr lµ viÕt t¾t cña Trace (vÕt cña ma trËn) :
Trace
aa a
aa a
aaaa
a
n
n
nn nn
ii
i
n
11 12 1
21 22 2
1211
1
...
...
... ... ... ...
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
==
∑
Hay :
[]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
2
2
2
y
x
= zyx .
zz
y
x
Do vËy
&(&.&)(.. .rTrrr Tr
d
dt Tr
d
dt Tr
TiiiTiT2== )
TS. Ph¹m §¨ng Ph−íc

Robot c«ng nghiÖp 88
=⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
== ∑∑
Tr T
qqr T
qqr
i
jjiiT
kkiT
k
i
j
i∂
∂
∂
∂
&.&
11
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=∑∑
==
i
jkj
k
T
i
Tii
j
i
i
k
qq
q
T
rr
q
T
Tr
11
.&&
∂
∂
∂
∂
(7.13)
7. 5. 2. TÝnh ®éng n¨ng cña vi khèi l−îng dm.
Ký hiÖu Ki lµ ®éng n¨ng cña kh©u thø i. dKi lµ ®éng n¨ng cña vi khèi l−îng dm ®Æt
t¹i vÞ trÝ ir trªn kh©u thø i.
dK Tr T
qrr T
qqq
ik
ii
j
iiT iT
kjk
j
i
=⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
== ∑∑
1
211
∂
∂
∂
∂
.&& dm
=⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
== ∑∑
1
211
Tr T
qrdm r T
qqq
k
ii
j
iiT
iT
kjk
j
i∂
∂
∂
∂
(. . ). && (7.14)
Vµ do ®ã ®éng n¨ng cña kh©u thø i sÏ lµ :
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
== ∑∫
∑
∫==
i
jkj
k
T
i
Khau
Tii
j
i
i
k
iqq
q
T
dmrr
q
T
TrdKK
1i
1
)..(
2
1&&
∂
∂
∂
∂
i Khau
(7.15)
§Æt gäi lµ ma trËn gi¶ qu¸n tÝnh (Pseudo inertia matrix).
∫
=
i
Tii rr.
Khau
idmJ
ý nghÜa "gi¶ qu¸n tÝnh" ®−îc sö dông v× khi thiÕt lËp ®Çy ®ñ c¸c phÇn tö cña ma trËn Ji ta
cã thÓ liªn hÖ víi c¸c kh¸i niÖm "m«men qu¸n tÝnh ®éc cùc" vµ tr×nh bµy c¸c phÇn tö cña Ji
gièng nh− c¸c phÇn tö cña m«men qu¸n tÝnh ®éc cùc. Ta xÐt mèi quan hÖ nÇy nh− sau :
Theo ®Þnh nghÜa ta cã :
= J
∫
=
i
Tii rr.
Khau
idmJ i = (7.16)
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
∫∫∫∫ ∫∫∫∫ ∫∫∫∫ ∫∫∫∫
dmzdmydmxdm
zdmdmzzdmyzdmx
ydmzdmydmyydmx
xdmzdmxydmxdmx
iii
iiiiii
iiiiii
iiiiii
2
2
2
B©y giê ta nh¾c l¹i m«men qu¸n tÝnh ®éc cùc cña
mét vËt thÓ bÊt kú nh− h×nh vÏ.
z
y x ω Theo ®Þnh nghÜa ta cã :
∫+= dmzy
xx )(I 22
∫+= dmzx
yy )I 22
∫+= dmyx
zz )(I 22
H
×nh 7.2 : M«men qu¸n tÝnh ®éc cùc
Vµ v× : )(
2
1
)(
2
1
)(
2
1
x2222222 yxzxzy +++++−=
VËy : ; .v.v… 2/)I I I( zzyyxx
2++−=
∫dmx
Ngoµi ra ta cßn cã :
; ;
∫
=xydm
xy
I∫
=yzdm
yz
I∫
=xzdm
xz
I
; ;
∫
=xdmmx ∫
=ydmmy ∫
=zdmmz
TS. Ph¹m §¨ng Ph−íc


























