
phßng gd - ®t huyÖn ®«ng hng
tr êng thcs ®«ng hoµng céng hoµ x· héi chñ nghÜa viÖt nam
§éc lËp - Tù do - H¹nh phóc
==== ====
s¸ng kiÕn kinh nghiÖm
n©ng cao chÊt lîng
häc sinh giái líp 8
i. c¬ së lý luËn
XuÊt ph¸t tõ môc tiªu ®µo t¹o cña Bé gi¸o dôc - §µo t¹o vµ sù ®æi
míi ph¬ng ph¸p d¹y häc nªn ®ßi hái mçi gi¸o viªn ph¶i kh«ng ngõng häc
tËp vµ nghiªn cøu khoa häc ®Ó ®¸p øng nh÷ng yªu cÇu míi trong t×nh
h×nh míi.
Ch¬ng tr×nh To¸n líp 8, phÇn “ Ch¬ng tr×nh chøa Èn trong dÊu
gi¸ trÞ tuyÖt ®èi”- dµnh cho häc sinh kh¸ - giái lµ mét trong nh÷ng
phÇn khã. Muèn n¾m ®îc c¸c c¸ch gi¶i cña d¹ng to¸n nµy häc sinh ph¶i
n¾m v÷ng ®Þnh nghÜa gi¸ trÞ tuyÖt ®èi. NhiÒu häc sinh gÆp trë ng¹i
khi gi¶i d¹ng to¸n nµy, lóng tóng khi gi¶i bµi to¸n cã dÊu gi¸ trÞ tuyÖt ®èi.
ChÝnh v× lý do trªn t«i m¹nh d¹n nghiªn cøu vµ ®a ra s¸ng kiÕn
“Ph¬ng tr×nh chøa Èn trong dÊu gi¸ trÞ tuyÖt ®èi”. Víi mong muèn
thiÕt thùc gióp häc sinh hiÓu bµi vµ lµm bµi tèt h¬n. Hi väng sÏ ®em l¹i
kÕt qu¶ tèt cho c¸c em.
ii. Néi dung s¸ng kiÕn
§Ó gi¶i c¸c ph¬ng tr×nh chøa Èn trong dÊu gi¸ trÞ tuyÖt ®èi, cÇn
khö dÊu gi¸ trÞ tuyÖt ®èi. Nhí l¹i kiÕn thøc: Gi¸ trÞ tuyÖt ®èi cña mét
biÓu thøc b»ng chÝnh nã nÕu biÓu thøc kh«ng ©m, b»ng sè ®èi cña
nãi nÕu biÓu thøc ©m:
=A
A nÕu A≥ 0
1

-A nÕu A<0
* Ph¬ng ph¸p 1: Ph¬ng ph¸p chia kho¶ng trªn trôc sè.
§Ó khö dÊu gi¸ trÞ tuyÖt ®èi, cÇn xÐt gi¸ trÞ cña biÓu lµm cho
biÓu thøc kh«ng ©m hay ©m. NÕu biÓu thøc n»m trong dÊu gi¸ trÞ
tuyÖt ®èi lµ nhÞ thøc bËc nhÊt, ta cÇn nhí ®Þnh lý sau:
- §Þnh lý vÒ dÊu cña nhÞ thøc bËc nhÊt ax + b (a
≠
0)
NhÞ thøc ax + b (a
≠
0)
- Cïng dÊu víi a víi c¸c gi¸ trÞ cña x lín h¬n nghiÖm cña nhÞ thøc.
- Tr¸i dÊu víi a víi c¸c gi¸ trÞ cña x nhá h¬n nghiÖm cña nhÞ thøc.
Chøng minh:
Gäi x0 lµ nghiÖm cña nhÞ thøc ax + b th×:
a
b
x−
=
0
. XÐt
x
x
a
b
x
a
bax
0
−=+=
+
- NÕu x > x0 th× x – x0 > 0 ⇒
bax
a
bax +⇒>
+0
cïng dÊu víi a.
- NÕu x < x0 th× x – x0< 0 ⇒
bax
a
bax +⇒<
+0
tr¸i dÊu víi a.
VÝ dô 1: Gi¶i ph¬ng tr×nh
45212 =−+− xx
(1)
Lêi gi¶i:
LËp b¶ng khö dÊu gi¸ trÞ tuyÖt ®èi.
x
2
1
2
5
12 −x
- 2x + 1
0
2x – 1 2x – 1
2

52 −x
- 2x + 5 - 2x +5 0 2x - 5
VÕ tr¸i - 4x + 6 4 4x - 6
Tõ ®ã ta xÐt 3 trêng hîp sau:
a) xÐt
2
1
<x
(1) Trë thµnh - 4x + 6 = 4 ⇔
2
1
<x
, kh«ng phô thuéc kho¶ng ®ang
xÐt.
b) XÐt
2
5
2
1<≤ x
(1) Trë thµnh 4 = 4 ®óng víi mäi x thuéc kho¶ng ®ang xÐt tøc lµ:
2
5
5
1<≤ x
c) XÐt
2
5
≥x
(1) trë thµnh 4x – 6 = 4 ⇔
2
5
=x
thuéc kho¶ng ®ang xÐt.
KÕt luËn: NghiÖm cña ph¬ng tr×nh (1) lµ
2
5
2
1≤≤ x
* Ph¬ng ph¸p 2: Ph¬ng ph¸p biÕn ®æi t¬ng ®¬ng
Ta ¸p dông hai phÐp biÕn ®æi c¬ b¶n sau:
(1)
−=
=
≥
⇔=
ba
ba
b
ba
0
(2)
−=
=
⇔= ba
ba
ba
VÝ dô 2: Gi¶i ph¬ng tr×nh:
531 −=− xx
(2)
3

Lêi gi¶i: ¸p dông phÐp biÕn ®æi thø hai ta cã:
(2)
=
=
⇔
+−=−
−=−
⇔
2
3
2
531
531
x
x
xx
xx
KÕt luËn: Ph¬ng tr×nh (2) cã hai nghiÖm:
2
3
;2 21 == xx
NhËn xÐt: Ta cã thÓ sö dông ph¬ng ph¸p 1 ®Ó gi¶i ph¬ng tr×nh (2).
* Ph¬ng ph¸p 3: Ph¬ng ph¸p ®Æt Èn phô:
VÝ dô 3: Gi¶i ph¬ng tr×nh:
1110255 22 −+−=+− xxxx
(3)
Lêi gi¶i:
(3)
( )
155255
22
=+−−=+−⇔ xxxx
§Æt
txx =+− 55
2
th× ph¬ng tr×nh trë thµnh
12 −−= tt
1
1
3
1
2
1
12
12
012
−=⇔
−=
−=
−≤
⇔
+=
−−=
≥−−
⇔t
t
t
t
tt
tt
t
=
=
⇔=+−⇔−=+− 3
2
065125 22
x
x
xxxx
* Ph¬ng ph¸p 4: Sö dông ®å thÞ:
Nguyªn t¾c: NghiÖm cña ph¬ng tr×nh f(x) = g(x) chÝnh lµ hoµnh
®é ®iÓm chung cña hai ®å thÞ y = f(x) vµ y – g(x).
VÝ dô 4: BiÖn luËn sè nghiÖm cña ph¬ng tr×nh:
4
mxxx =+++− 11
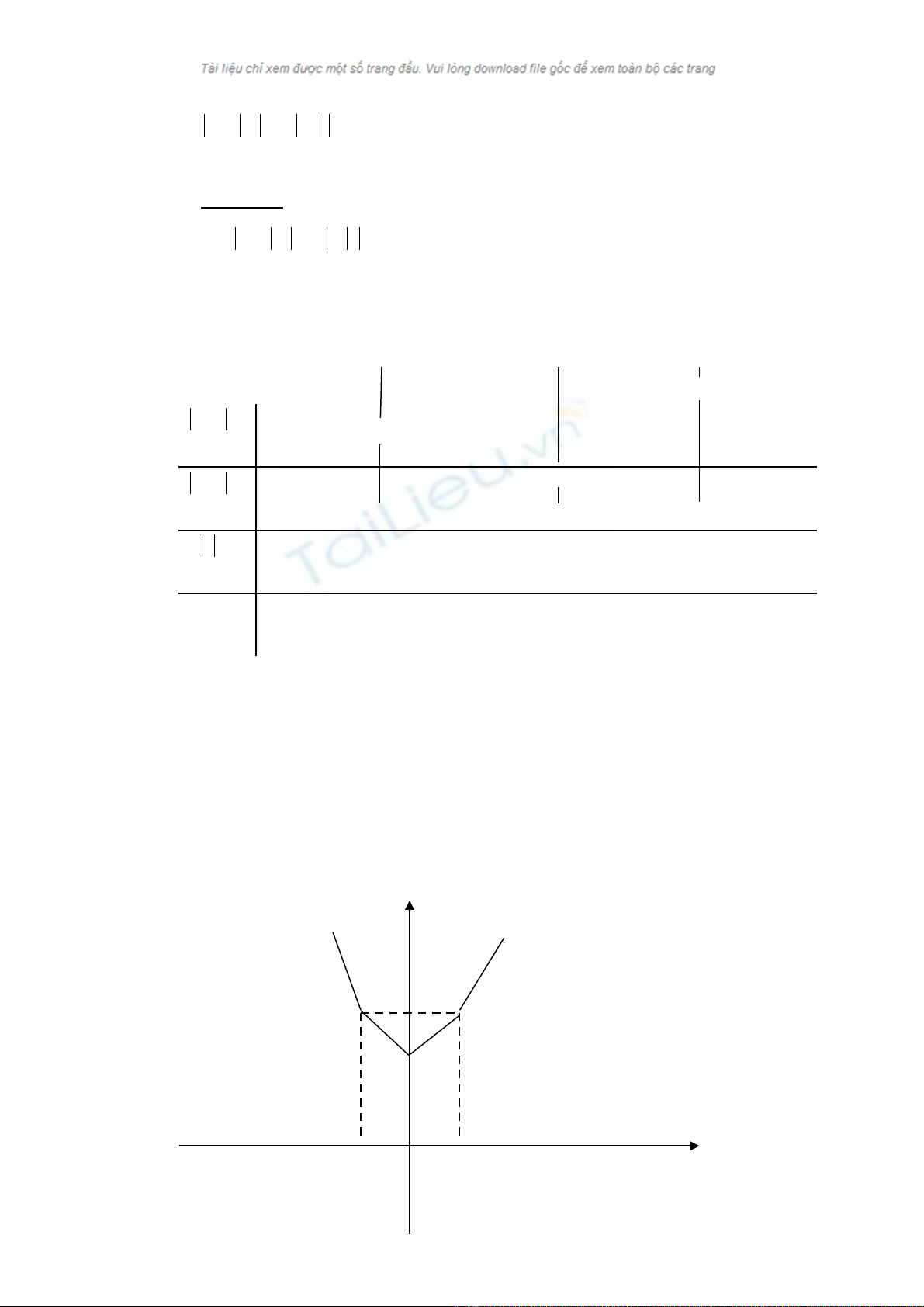
Lêi gi¶i: Tríc hÕt ta vÏ ®å thÞ hµm sè:
xxxy +++−= 11
+ LËp b¶ng khö dÊu gi¸ trÞ tuyÖt ®èi:
x -1 0
1
1−x
-x + 1 -x + 1 -x + 1
0
x – 1
1+x
-x – 1
0
x + 1 x + 1 x + 1
x
-x -x
0
x x
y -3x
3
-x + 2
2
x + 2
3
3x
VÏ ®å thÞ trªn tõng kho¶ng chó ý c¸c ®iÓm ®Æc biÖt:
A(-1;3) ; B(0;2) ; C(1;3);
Sè nghiÖm cña ph¬ng tr×nh ®óng b»ng sè ®iÓm chung cña ®êng
th¼ng
y = m víi ®å thÞ võa vÏ.
3
B 2
-1 0 1
5
x
y
AC




































