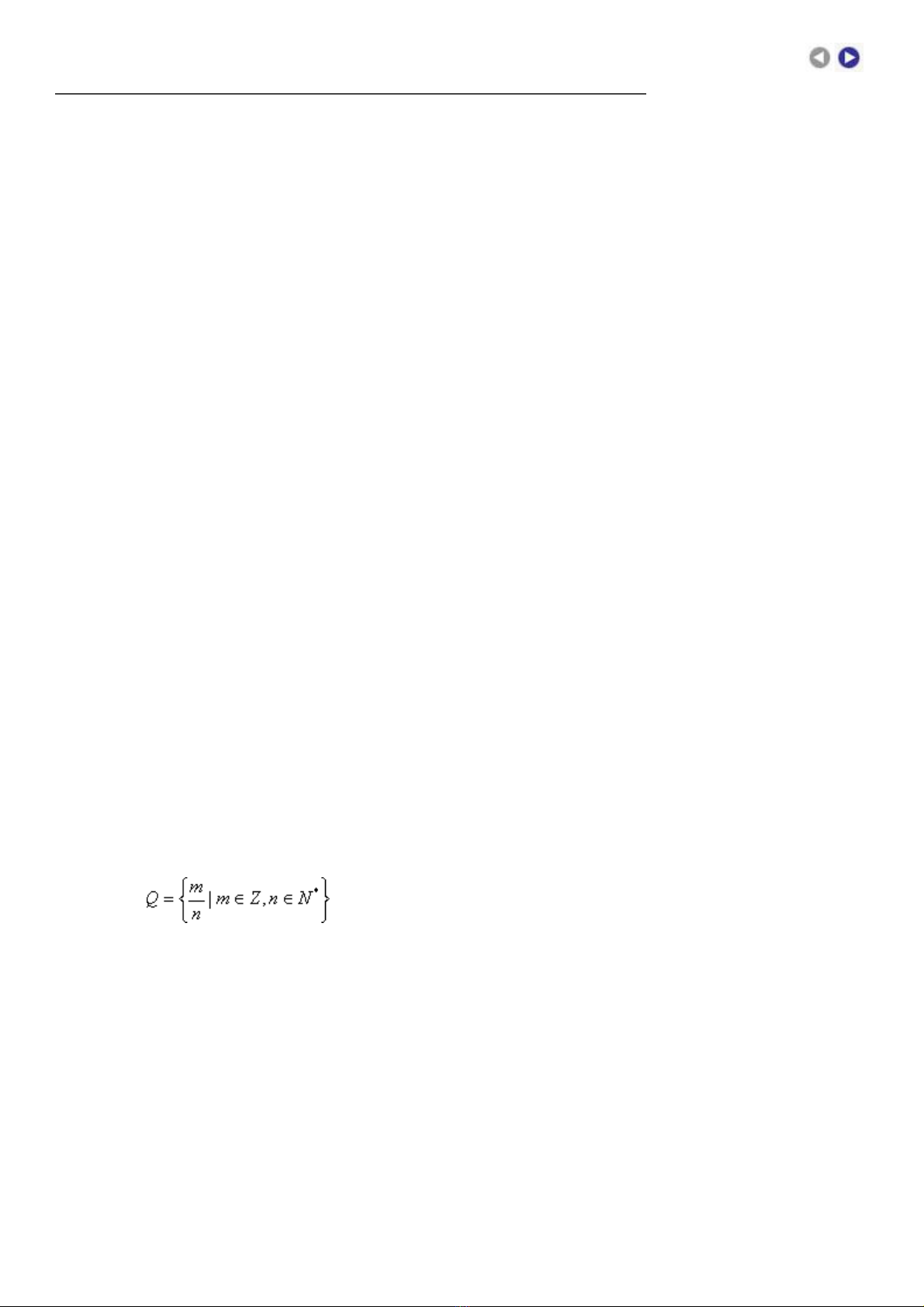
T
ậ
p h
ợp
1. Mét sè kh¸i niÖm
+
TËp hîp A, chøa c¸c phÇn tö x, y, ...,
A = {x, y, ...}, x
A, y
A
+
TËp hîp A chøa c¸c phÇn tö x tháa m·n
®
iÒu kiÖn P.
A = {x\ x tháa m·n
®
iÒu kiÖn P}
+
gäi l
µ
tËp rçng (tËp hîp kh
«
ng cã phÇn tö).
+
A
B th× A l
µ
tËp con cña tËp B.
+
A = B th× tËp A v
µ
tËp B ®
Òu l
µ
tËp con cña nhau.
2. C¸c phÐp to¸n vÒ tËp hîp
+
Hîp
A
B = {x
A hoÆc x
B}
+
A
B = B
A ; (A
B)
C = A
(B
C)
A
A = A ; A
A
B ; B
A
B
A
= A
+
Giao
A
B = {x
A v
µ
x
B}
+
A
B = B
A ; A
B
B ; A
B
A
A
A = A ; (A
B)
C = (A
C)
(B
C)
A
=
; (A

B)
C = (A
C)
(B
C)
+
(A
B)
C = A
(B
C)
+
HiÖu
A \ B = {x | x
A v
µ
x
B}
A \ A =
(A \ B)
C = (A
C) \ B = (A
C) \ (B
C)
A \ B = A \ (A
B)
A = (A
B)
(A \ B)
+
PhÇn bï
C
A
S = A\ S (S
A)
3. TËp hîp sè
+
TËp hîp sè tù nhi
ª
n
N = {0, 1, 2, ...}
+
TËp hîp sè nguy
ª
n
Z = {...
-
2,
-
1, 0, 1, 2, ...}
+
TËp hîp sè h÷u tØ
+ TËp hîp sè thùc
R = {a0
, a
1
, a
2
, ...| a
0
Z, ak
{0, 1, 2, ..., 9}}
Nh
vËy ta cã :
N
Z
Q
R
1. TÝnh chÊt c¸c phÐp to¸n tr
ª
n sè
+
TÝnh chÊt giao ho¸n cña phÐp céng v
µ
nh
©
n
a + b = b + a
ab = ba
+
TÝnh chÊt kÕt hîp cña phÐp céng v
µ
nh
©
n
(a + b) + c = a + (b + c)
(a.b).c = a.(b.c)
+
TÝnh chÊt ph
©
n phèi cña phÐp nh
©
n ®
èi víi phÐp céng
(a + b)c = ac + bc
+
TÝnh chÊt ph
©
n phèi cña phÐp nh
©
n ®
èi víi phÐp trõ
(a
-
b)c = ac
-
bc
2. BiÓu thøc ph
©n
+
TÝnh chÊt c
¬ bn cña ph
©
n thøc
+
C¸c phÐp to¸n cña ph
©
n thøc
3. TØ lÖ thøc
+
TØ lÖ thøc l
µ
mét
®
¼ng thøc cña hai tØ sè
a, d l
µ
hai ngo
¹
i tØ ; b, c l
µ
hai trung tØ.
+
TÝnh chÊt c
¬
bn cña tØ lÖ thøc :
ad = bc
+
Mét sè tÝnh chÊt kh¸c
Víi a, b, c, d
0 v
µ
th× :
BiÓu thøc ®¹i sè
Lòy thõa
C¨n bËc n
Luü thõa vµ c¨n sè
+
Mét sè
®
Þnh nghÜa
* Luü thõa sè mò nguy
ª
n
* Luü thõa sè mò h÷u tØ
* Luü thõa sè mò v
«
tØ
(a > 0, x l
µ
sè v
«
tØ > 0)
(x
n
)
l
µ
d·y sè gÇn
®
óng thiÕu cña x)
+
C¸c tÝnh chÊt c
¬
bn cña luü thõa
Gi sö a > 0, b > 0
x, y
R ta cã :
+
Mét sè tÝnh chÊt kh¸c
*
x, y
R, x < y
+ Víi a > 1
a
x
< a
y
+ Víi 0 < a < 1
a
x
> a
y
* (x
n
)
R, a > 0 m
µ
:
Luü thõa
+
§Þnh nghÜa : n
N
*
, c¨n bËc n cña sè a l
µ
mét sè b sao cho
bn
= a,
kÝ hiÖu l
µ
*
Mäi sè a chØ cã mét c¨n bËc lÎ
* Sè
©
m kh
«
ng cã c¨n bËc ch½n
* Sè d¬
ng cã hai c¨n bËc ch½n, hai c¨n Êy cã sè trÞ
®
èi nhau. Gi¸ trÞ d
¬
ng cña c¨n bËc ch½n n cña sè a > 0 kÝ
hiÖu l
µ
.
+
víi a > 0 gäi l
µ
c¨n sè häc
+
C¨n bËc n