1
LỜI NÓI ĐẦU
Cơ học ứng dụng là một phần kiến thức căn bản đối với kỹ sư thuộc các ngành
kỹ thuật, vì vậy môn học này được bố trí trong chương trình đào tạo của nhiều trường
đại học như: đại học Bách khoa Hà Nội, Giao thông vận tải, Thuỷ lợi, Xây dựng,… Ở
trường Đại học Sư phạm Kỹ thuật Nam Định, môn học này được giảng dạy cho sinh
viên hệ đại học chuyên nghành Điện- Điện tử. Hiện nay, các trường đại học đều có tài
liệu riêng giảng dạy về môn học này với các tên gọi khác nhau như Cơ học cơ sở, Cơ
học kỹ thuật v.v.. với nội dung thời lượng và khối lượng kiến thức rất khác nhau do
đặc thù của ngành.
Chính vì vậy việc biên soạn một bài giảng môn học Cơ học ứng dụng riêng cho
sinh viên trường Đại học Sư phạm Kỹ thuật Nam Định là rất cần thiết. Theo chương
trình môn học Cơ học ứng dụng được xây dựng để giảng dạy cho sinh viên trường Đại
học Sư phạm Kỹ thuật Nam Định, nội dung của môn học bao gồm ba phần: Cơ học vật
rắn tuyệt đối, cơ học vật rắn biến dạng (Sức bền vật liệu) và chi tiết máy, trong đó
phần Cơ học vật rắn tuyệt đối và chi tiết máy được viết gộp trong 3 chương bao gồm
nội dung về tĩnh học, động học và động lực học chất điểm và cơ hệ. Phần Cơ học vật
rắn biến dạng được viết trong 1 chương bao gồm các nội dung về các hình thức chịu
lực đơn giản và phức tạp của thanh.
Cuốn bài giảng được viết trên cơ sở chương trình môn học Cơ học ứng dụng.
Người biên soạn đã cố gắng trình bày những vấn đề cơ bản của Cơ học theo quan điểm
hiện đại, đảm bảo tính sư phạm và yêu cầu chất lượng của một bài giảng giảng dạy đại
học. Những kiến thức trình bày trong bài giảng này là những kiến thức tối thiểu, cần
thiết nhằm trang bị các kiến thức cơ học nền tảng trong hệ thống kiến thức cung cấp
cho các sinh viên, đặc biệt cho các sinh viên phi cơ khí.
Cuốn bài giảng được biên soạn lần đầu nên chắc chắn còn nhiều thiếu sót.
Chúng tôi rất mong nhận được sư góp ý của các đồng nghiệp và các em sinh viên để
có điều kiện sửa chữa, hoàn thiện hơn cuốn bài giảng nhằm phục vụ tốt hơn cho công
tác giảng dạy và học tập. Các ý kiến đóng góp xin gửi về địa chỉ: Bộ môn Kỹ thuật cơ
sở, Khoa cơ khí, Trường Đại học Sư phạm kỹ thuật Nam Định.
Nhóm tác giả biên soạn
2
3
MỤC LỤC
LỜI NÓI ĐẦU ................................................................................................................. 1
MỤC LỤC ....................................................................................................................... 3
Phần 1: CƠ HỌC VẬT RẮN TUYỆT ĐỐI……………………………………………5
Chương 1 ......................................................................................................................... 5
ĐỘNG HỌC .................................................................................................................... 5
1.1. ĐỘNG HỌC ĐIỂM .............................................................................................. 5
1.1.1. Phương pháp véc tơ ....................................................................................... 5
1.1.2. Phương pháp toạ độ Đề các ........................................................................... 7
1.1.3. Phương pháp toạ độ tự nhiên ......................................................................... 9
1.1.4. Một số chuyển động thường gặp ................................................................. 12
1.2. ĐỘNG HỌC VẬT RẮN TUYỆT ĐỐI .............................................................. 14
1.2.1. Các chuyển động cơ bản của vật rắn ........................................................... 14
1.2.2. Chuyển động song phẳng của vật rắn .......................................................... 22
1.3. HỢP CHUYỂN ĐỘNG CỦA ĐIỂM- VẬT RẮN ............................................. 33
1.3.1. Hợp chuyển động của điểm ......................................................................... 33
1.3.2. Hợp chuyển động của vật rắn ...................................................................... 37
1.4. ĐỘNG HỌC CƠ CẤU ....................................................................................... 42
1.4.1. Một số khái niệm ......................................................................................... 42
1.4.2. Cơ cấu bốn khâu bản lề phẳng .................................................................... 42
1.4.3. Các biến thể của cơ cấu bốn khâu ............................................................... 43
1.4.4. Cơ cấu cam .................................................................................................. 45
1.4.5. Cơ cấu bánh răng ......................................................................................... 46
CÂU HỎI ÔN TẬP ....................................................................................................... 51
Chương 2 ....................................................................................................................... 52
TĨNH HỌC .................................................................................................................... 52
2.1. CÁC KHÁI NIỆM CƠ BẢN VÀ CÁC ĐỊNH LUẬT TĨNH HỌC ................... 52
2.1.1. Các khái niệm cơ bản .................................................................................. 52
2.1.2. Các định luật tĩnh học .................................................................................. 57
2.1.3. Các hệ quả ................................................................................................... 61
2.2. KHẢO SÁT HỆ LỰC ........................................................................................ 64
2.2.1. Hệ lực phẳng ................................................................................................ 64
2.2.2. Hệ lực không gian ....................................................................................... 74
CÂU HỎI ÔN TẬP ....................................................................................................... 83
Chương 3 ....................................................................................................................... 84
ĐỘNG LỰC HỌC ......................................................................................................... 84
3.1. CÁC ĐỊNH LUẬT CƠ BẢN CỦA ĐỘNG LỰC HỌC VÀ PHƯƠNG TRÌNH
VI PHÂN CHUYỂN ĐỘNG CỦA CHẤT ĐIỂM .................................................... 84
3.1.1. Các khái niệm .............................................................................................. 84
3.1.2. Các định luật cơ bản của động lực học ........................................................ 84
3.1.3. Phương trình vi phân chuyển động của chất điểm ..................................... 86
3.1.4. Hai bài toán cơ bản của động lực học ......................................................... 87
3.2 ĐỘNG LỰC HỌC CƠ HỆ .................................................................................. 89
3.2.1. Các khái niệm .............................................................................................. 89
3.2.2. Nguyên lý Đalămbe ..................................................................................... 93
3.3 CÁC ĐỊNH LÝ TỔNG QUÁT CỦA ĐỘNG LỰC HỌC CƠ HỆ ...................... 96
4
3.3.1. Định lý động lượng và định lý chuyển động khối tâm ................................ 97
3.3.2. Định lý mômen động lượng ....................................................................... 102
3.3.3. Định lý động năng ..................................................................................... 106
3.3.4. Định lý bảo toàn cơ năng ........................................................................... 114
3.4. ĐỘNG LỰC HỌC VẬT RẮN ......................................................................... 117
3.4.1. Vật rắn chuyển động tịnh tiến ................................................................... 117
3.4.2. Vật quay xung quanh một trục cố định với vận tốc góc
gia tốc góc
117
3.4.3. Vật rắn là tấm phẳng chuyển động song phẳng......................................... 118
CÂU HỎI ÔN TẬP ..................................................................................................... 120
Phần 2: CƠ HỌC VẬT RẮN BIẾN DẠNG ………………………………………121
Chương 4 ..................................................................................................................... 121
CƠ HỌC VẬT RẮN BIẾN DẠNG............................................................................. 121
4.1. MỞ ĐẦU .......................................................................................................... 121
4.1.1. Các khái niệm về thanh ............................................................................. 121
4.1.2. Nội lực- Ứng suất ...................................................................................... 122
4.1.3. Phương pháp mặt cặt biến thiên- các thành phần nội lực trên mặt cắt ngang
............................................................................................................................. 123
4.1.4. Quan hệ giữa ứng suất và các thành phần nội lực trên mặt cắt ngang ...... 124
4.1.5. Biến dạng ................................................................................................... 125
4.1.6. Các giả thiết cơ bản về vật liệu ................................................................. 126
4.2. KÉO- NÉN ĐÚNG TÂM ................................................................................. 127
4.2.1. Khái niệm .................................................................................................. 127
4.2.2. Nội lực và biểu đồ nội lực ......................................................................... 127
4.2.3. Ứng suất trên mặt cắt ngang ...................................................................... 128
4.2.4. Điều kiện cường độ- ba bài toán cơ bản .................................................... 134
4.3. XOĂ
N THUÂ
N TU
Y CU
A THANH THĂ
NG ............................................... 135
4.3.1. Khái niệm .................................................................................................. 135
4.3.2. Nô
i lưc va biêu đô nô
i lưc ......................................................................... 136
4.3.3. Ứng suất trên mặt cắt ngang ...................................................................... 137
4.3.4. Điều kiện cường độ– ba bài toán cơ bản ................................................... 141
4.4. UỐN PHẲNG CỦA THANH THẲNG ........................................................... 143
4.4.1. Khái niệm .................................................................................................. 143
4.4.2. Nội lực và biểu đồ nội lực ......................................................................... 143
4.4.3. Ứng suất trên mặt cắt ngang ...................................................................... 146
4.4.4. Điều kiện cường độ- ba bài toán cơ bản .................................................... 154
4.5. THANH CHỊU LỰC PHỨC TẠP .................................................................... 156
4.5.1. Thanh chịu uốn xiên .................................................................................. 158
4.5.2. Uốn và kéo (nén) đồng thời ....................................................................... 161
4.5.3. Kéo (nén) lệch tâm .................................................................................... 165
4.5.4. Xoắn và uốn đồng thời .............................................................................. 167
4.5.5. Thanh chịu lực tổng quát ........................................................................... 171
CÂU HỎI ÔN TẬP ..................................................................................................... 172
TÀI LIỆU THAM KHẢO ........................................................................................... 173
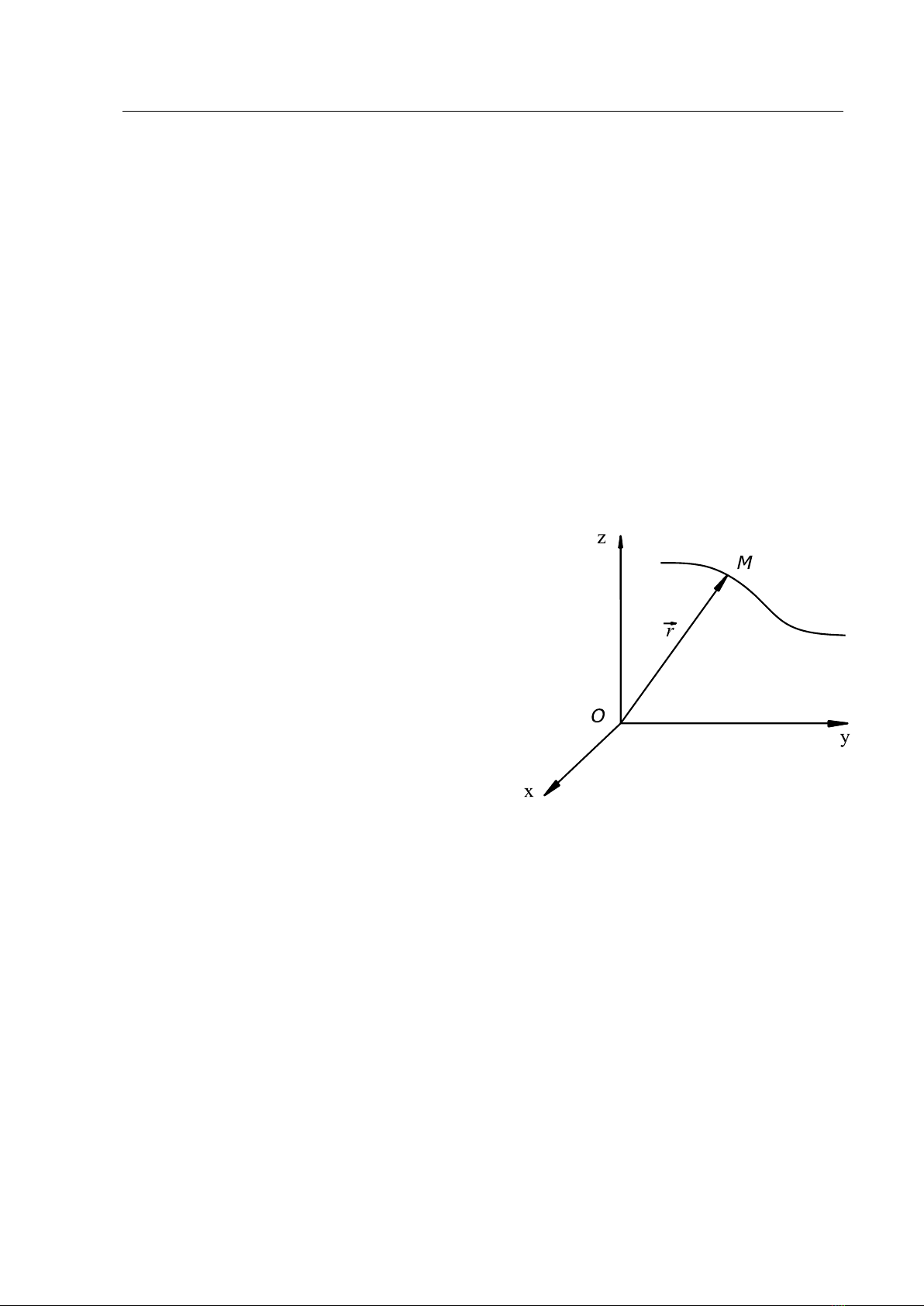
5
Phần 1: CƠ HỌC VẬT RẮN TUYỆT ĐỐI
Chương 1
ĐỘNG HỌC
1.1. ĐỘNG HỌC ĐIỂM
Trong phần động học điểm, chúng ta khảo sát chuyển động của một điểm đối
với một hệ quy chiếu đã chọn. Để mô tả sáng sủa và gọn gàng các đặc trưng của
chuyển động, chúng ta sử dụng phương pháp véc tơ. Để tính toán thuận tiện, chúng ta
sử dụng các phương pháp tọa độ như phương pháp tọa độ Đềcác, phương pháp tọa độ
tự nhiên, phương pháp véc tơ.
1.1.1. Phương pháp véc tơ
1.1.1.1. Phương trình chuyển động
Xét điểm M chuyển động trong hệ quy chiếu Oxyz (Hình 1.1).
Vị trí của điểm M được xác định bởi
véc tơ
OMr
. Điểm M chuyển động, do đó
r
thay đổi theo thời gian:
)(trr
(1.1)
Phương trình (1.1) được gọi là phương
trình chuyển động của điểm M dạng véc tơ.
Chú ý rằng điểm M chuyển động liên
tục, ở mỗi thời điểm, điểm M chiếm một vị trí
xác định và có hướng chuyển động xác định.
Do đó
)(tr
là một hàm liên tục, đơn trị.
Tập hợp các vị trí của điểm trong không gian quy chiếu được gọi là quỹ đạo của
nó trong hệ quy chiếu ấy. Phương trình (1.1) là phương trình tham số của quỹ đạo.
Nếu quỹ đạo là đường thẳng, thì chuyển động được gọi là chuyển động thẳng. Nếu quỹ
đạo là đường cong, thì chuyển động được gọi là chuyển động cong. Và khi đó, người
ta thường lấy tên đường cong quỹ đạo để gọi tên chuyển động
1.1.1.2. Vận tốc chuyển động
Một trong những đặc trưng cơ bản của chuyển động của điểm là khái niệm vận
tốc đối với một hệ quy chiếu đã chọn. Chúng ta sẽ xây dựng một cách chặt chẽ khái
niệm này. Giả sử ở thời điểm t, điểm ở vị trí M xác định bởi
OMr
. Ở thời điểm
khác t1 = t + ∆t, điểm ở vị trí M1 xác định bởi
1
1OMr
(Hình 1.2). Như thế sau
khoảng thời gian ∆t điểm dịch chuyển được một đoạn: